數控機床在機檢測中觸發式測頭誤差變速補償*

白 克，黎 智，吳立輝

(1. 河南經貿職業學院，鄭州 450000; 2. 四川省裝備制造業機器人應用技術工程實驗室，四川 德陽 618000; 3. 河南工業大學機電工程學院，鄭州 450052)

0 引言

觸發式測頭測量系統在數控機床上的應用較為廣泛[1-4]，但測頭的觸發半徑變化通常大于10 μm，這是造成在機測量誤差的重要原因，直接影響加工精度。為了提高測量精度，可以采用各種有效的方法[5]。其中，最明顯的一種方法就是為機床配備更加精確的測頭，例如非接觸式應變儀。但是，高精密的測頭價格比較昂貴。

由于測頭誤差產生的主要原因是系統誤差，因此提高機床測量精度的另一種方法是對測頭的系統誤差進行數字誤差校正。該方法已成功地應用于坐標測量機(coordinate measuring machines，CMM)專用測頭[6]，并且可以同樣有效地應用于數控機床的觸發式測頭[7]。例如，Jankowski M等[8]對數控機床測頭誤差的力學模型進行了研究，驗證了數值校正方法的可行性，并證實其精度受系統誤差的影響要比隨機誤差的影響大。崔星星等[9]對測頭預行程誤差進行了統計學相關分析，并提出采用神經網絡進行建模預測，分析結果也驗證了數字誤差校正的有效性。

但是，現有解決方案大多需要將錯誤數據上傳到機床控制器并由其執行計算。如果沿機床的單軸進行測量，則計算很簡單：只需將X、Y和Z坐標讀數加上或減去已知的系統誤差值即可。但是，若不沿單個軸進行測量時，由于必須分別在2或3個軸上進行校正，因此需要將每個測量方向上的3個誤差校正值(每個坐標一個)上傳到機床控制器，并使用三角函數進行計算來完成測量，導致計算會變得更加復雜。這意味著校正的效果在很大程度上取決于控制器的硬件和軟件，導致在機檢測系統誤差補償困難。

為克服該缺點，提出了一種新的測頭系統誤差變速補償方法。該方法的優點是，可以在進行在機測量之前，離線進行所有計算的新速度值。無需單獨計算三個校正值(X、Y和Z)。所提出的方法易于應用，可以輕松完成觸發式測頭在機測量，但其精度得到顯著提高，誤差可以降低10倍。

1 系統誤差建模

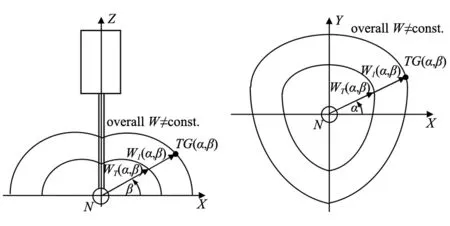
測頭的系統誤差可以用觸發半徑特性和變化值來描述。觸發半徑的定義如下[10]：在方向i上進行測量時，如果TGi表示探針尖端的位置，并且Os表示最佳擬合元素的中心(為各個方向的觸發點TG確定的)，則ri表示測量方向i上的觸發半徑，等于點Os和TGi之間的距離。觸發半徑變化量Vr表示測頭觸發半徑最大值和最小值之間的差。

觸發半徑變化與測球的形狀偏差相對應，因此可以利用它對測頭的實際性能進行很好地說明。然而，若使用另一個參數-預行程w，可以更方便地對測頭進行理論建模。該參數的定義方法為：如果探針尖端的中間位置由N表示，則用wi表示的方向i上的預行程，等于點N和TGi之間的距離。相對于測頭主體的中間位置N，每次測量所得的值可能會因測頭滯后等原因而有所不同。但是，通常假定它是常數，即假定其變化可以忽略不計。這兩個參數的圖形說明如圖1所示。

圖1 測頭觸發半徑和預行程的圖形解釋

假定點Os和N位于同一位置，則ri=wi。在實踐中很少滿足這一假設所需的條件，但是如果上述各點之間的距離足夠小，則可以假設為ri≈wi。為了完成本文的研究，進行了這一假設。

方向i可以由兩個角度α和β的值定義。α是方向i在垂直于測頭軸線的平面上的投影與該平面上所選定線之間的夾角，而β是方向i與垂直于測頭軸線的平面上之間的夾角。

先前的研究表明，在給定方向上的預行程與測量速度成正比：

w(α,β)=wT(α,β)+wI(α,β)=wT(α,β)+v(α,β)τ

(1)

式中，wT為與測頭換能器相關的預行程分量，wI為與測量速度相關的預行程分量，v為測量速度，τ為換能器觸發與測頭控制器輸出更改之間的延遲。

如果所有測量方向上的測量速度都相同，則所有測量方向上與測量速度相關的預行程分量也相等，如圖2所示。

(a) 側面示意 (b) 頂部示意圖2 實現恒定的測量速度所需的測頭預行程和總預行程

因此，有效探測半徑(探針尖端半徑減去預行程，即為了獲得工件表面上測量點的坐標而必須移動所測機床位置的距離)在不同方向上是不同的，而機床刀具控制器通常僅使用有效探測半徑的一個值。

所提出的測頭誤差補償方法就基于編程可變測量速度的，所以與測量速度相關的預行程分量也是可變的，但總預行程在每個方向上都是相等的。探測誤差僅受測頭隨機誤差的影響。

2 誤差變速補償方法

為了補償與測頭換能器相關的測頭預行程分量，與測量速度相關的預行程分量必須隨著與換能器有關的預行程分量的增加而減小，公式如下所示：

(2)

(a) 側面示意 (b) 頂部示意圖3 應用變速誤差補償方法后測頭的預行程和總預行程

為了達到這個目的，應按下式對測量速度值進行計算：

(3)

如上所述，預行程是適用于測頭行為建模的參數，但是在實踐中，觸發半徑更為重要。因此，可能需要用觸發半徑值替換公式(3)中的預行程值。在這種情況下，測頭誤差映射和測量速度值計算的一次迭代可能會不夠。在這樣的情況下，則應該多次執行速度測定，每次都使用之前計算的測量速度值v1作為v0值。

3 實驗結果與分析

分兩步對該方法進行了具體驗證：首先驗證其在實驗室中是否可以減小觸發半徑變化；然后驗證其真實在機測量環境中是否具有適用性。

3.1 實驗室測試

確定測頭誤差的最常用方法是在機床上對主工件進行測量[10]。在第一步中，通過使用測試裝置對提出的方法進行了實驗驗證。該裝置的方案如圖4所示。該裝置機械部分的照片如圖5所示。

1.測試測頭 2.探針尖端 3.主工件4.三軸向壓電工作臺 1.測試測頭 2.探針尖端 3.主工件4.三軸向壓電工作臺

固定測試測頭1，使其測頭尖端2位于主工件3的中心，主工件位于3軸壓電工作臺4上，其位置由控制單元設定。為了測試測頭在給定方向上的觸發半徑，主工件會通過壓電工作臺在該方向上移動，并讀取與測頭觸發點相對應的坐標。確定觸發半徑變化量的觸發半徑變化確定的擴展不確定度U(Vr)= 0.6 μm(當覆蓋因子k=2時)。

為了對本文的誤差補償方法進行驗證，將其應用于兩個三維觸發式測頭：雷尼紹OMP40-2和雷尼紹OMP60。按照文獻[10]中確定延遲的方法(根據平均觸發半徑測量獲得各種測量速度，從而推導出τ)獲得OMP40-2測頭的延遲τ值為12.68 ms，OMP60測頭的τ值為25.35 ms。兩種測頭的初始測量速度均設置為50 mm/min，并且兩種測頭均配有50 mm 長的探針。

在應用誤差補償方法之前，進行10次測量后確定OMP40-2的觸發半徑變化等于11.0 μm。β角不同時測頭的觸發半徑特征如圖6所示(所有顯示值均為10次測量后所取的平均值)。

圖6 誤差補償之前OMP40-2在不同β角下的觸發半徑特征

從圖6可以看出，觸發半徑特征呈現為3瓣形的。在β角的值較小時這種形狀較為顯著：當β=0°時，觸發半徑變化值Vr=8.6μm，而當β=80°時觸發半徑變化值Vr=2.3μm。這些結果與關于觸發式測頭的現有認知一致。觸發半徑特征的3瓣形是造成觸發半徑變化的主要原因。

應用誤差補償方法后，測量速度從26.46 mm/min變為69.87 mm/min，并且進行10次測量后觸發半徑變化減小到1.0 μm，這是測頭隨機誤差值。在不同β角時獲得的觸發半徑特征如圖7所示(所有給出的值均為10次測量后得到的平均值)。從圖7可以看出，空間觸發半徑特征是準球形的。這意味著已經成功消除測頭的系統誤差。

圖7 誤差補償后OMP40-2在不同β角下的觸發半徑特征

當使用OMP60測頭時，觸發半徑變化是在進行誤差補償之前進行10次測量得出的，等于16.8 μm。應用誤差補償之前在不同β角時獲得的測頭觸發半徑特征如圖8所示(所有值均為10次測量后取得的平均值)。從圖8可以看出，與OMP40-2測頭的情況相同，觸發半徑是3瓣形的，這是三維觸發式測頭的典型特征。

圖8 誤差補償前OMP60在不同β角下的觸發半徑特征

應用所提出的誤差補償方法后，該形狀會消失。測量速度從31.24 mm/min變化到66.18 mm/min，10次測量后確定的觸發半徑變化降至1.0 μm。不同β角的改進后準圓形觸發半徑特征如圖9所示(所有值為10次測量后得到的平均值)。從圖9可以看出，與OMP40-2測頭的情況一樣，系統誤差得到消除。

圖9 誤差補償后OMP60在不同β角下的觸發半徑特征

3.2 數控機床在機檢測

在實驗室裝置上進行的測試結果，證實所提出的方法能夠將測頭的系統誤差降低10倍以上。為了驗證采用本文方法后，是否會減少在機檢測觸發式測頭系統(包括測頭和機床)的誤差，對測球進行了在機測量。第三個測頭是OMP40-2(非實驗室測試中使用的OMP40-2)，配有100 mm長的探針，并且使用了Haas VF7數控機床。

為了確定該測頭的延遲，對標稱為52 mm的規環進行了15次在機測量：分別以50 mm/min的恒定速度進行5次測量，以100 mm/min的恒定速度進行5次測量，以150 mm/min的恒定速度進行5次測量。每次在36個點對環進行測量。按照文獻[10]中確定延遲的方法，通過所獲得的數據可計算出延遲時間τ=14.5ms。

為了確定所用測頭的系統誤差，以100 mm/min的恒定速度對測球進行了10次測量，每次測量109個點。所獲得的形狀偏差等于測頭的系統誤差，如圖10所示(顯示的值是10次測量所獲得的平均值)。

圖10 不同的β角下所測球的測量形狀偏差 (等于機床上所用OMP40-2的系統誤差)

假設測球的形狀誤差可以忽略不計，考慮到10次測量所獲得的平均值，則在Haas VF7數控機床上所得的探測誤差的系統分量等于21 μm處測量的形狀誤差。由于隨機誤差的原因，單次測量中的形狀誤差會更大，獲得的最大值為23 μm。

完成上述測量后，計算出一組新的測量速度值(最小值為43.594 mm/min，最大值為131.277 mm/min)，并使用這些新的速度值進行了10次測量。所獲得的結果如圖11所示(顯示的值是10次測量后所得的平均值，等于機床上所使用OMP40-2的系統誤差)。

圖11 誤差補償后不同β角下所測球的測量形狀偏差

從圖11可以看出，根據10次測量所得到的數據，可知測得的形狀偏差等于2 μm。單次測量獲得的形狀誤差的最大值為6 μm。這表明，同樣在機床上，所提出的方法可以將測頭的系統誤差減少到超出探頭隨機誤差的水平。盡管需要執行多迭代的過程，但在實際測量環境中，該過程的第一次迭代就有效減小了系統誤差。

為了確定測量時間是否顯著增加，對相對增加時間ΔtR進行了計算(僅計算與測量速度有關的時間)，具體方法如下：

單個點處測量時間的速度相關分量ts等于：

(4)

式中，S為探針的接近距離，即從設置測量速度的點到被測量點之間的距離。

多點的測量時間tM是單點的測量時間之和：

(5)

式中，n為測量的次數。

為了確定由于應用誤差補償方法而導致的相對測量增加時間ΔtR，將應用方法之后的測量時間除以采用方法之前的測量時間，然后減去1：

(6)

根據該式可知，增加的測量時間主要取決于測量程序。在機床上進行109次測量后計算出的測量速度)，得出ΔtR=4.6%，可見應用方法之后的測量時間只是稍微有所延長。

4 結論

本文提出了一種新的測頭誤差補償方法，避免了使用數控機床控制器進行復雜的計算。該方法通過設

置適當的測量速度，實現了測頭誤差的顯著減小。對三維觸發式測頭進行的實驗得出如下結論：①提出的誤差變速補償可以輕松完成觸發式測頭在機測量，且控制器無需進行任何運算，驗證了其適用性；②在機測量精度得到顯著提高，誤差可以降低10倍，驗證了提出方法的先進性。但是測量時間稍微有所延長，因此將在后續的研究中對此開展進一步研究。