基于觀測器的壓邊裝置自適應滑模同步控制*

湯 澍，施光林，林杰克，楊培中

(上海交通大學機械與動力工程學院，上海 200240)

0 引言

立式旋壓加工因能夠克服超大型曲母線回轉薄壁制件由傳統分瓣拼焊工藝帶來的效率低、成品力學性能差等問題，成為了這類制件未來加工的必然趨勢，但其也容易導致板坯發生邊緣褶皺、失穩開裂等旋壓失效問題[1]。隨動壓邊裝置是針對大型立式并聯旋壓機旋壓失效問題做出的特殊設計，其在工作過程中除了高精度位置控制要求外，各執行器之間還需滿足同步性要求。但由于電液比例控制系統本身具有高度非線性、內部參數難確定的特點，且壓邊裝置在工作過程中還會受到板坯起皺反力、耦合偏置力等未知擾動的影響，使得為該裝置設計高性能控制器相當具有挑戰性[2-3]。

滑模控制作為一種結構簡單且具有較強魯棒性的控制方法，被廣泛應用于非線性控制領域[4-5]。文獻[6]提出了一種自適應滑模控制方法，引入平滑飽和函數改善滑模控制的震顫，并利用系統辨識方法修正滑模控制量；文獻[7]提出了一種雙曲正弦函數滑模指數趨近律，并利用反步法設計滑模控制器，提高系統收斂速度；文獻[8-9]將滑模控制與智能控制結合起來，通過引入模糊神經網絡或模糊邊界層的方式，增強系統抗干擾能力，解決抖振問題；文獻[10-11]均對滑模控制的積分特性進行了研究，通過在滑模面中引入積分項提高系統穩態精度。上述方法均對提高系統控制精度做出了有效的嘗試，但當系統擾動較大時，控制精度會有所折扣。且大部分研究重心均集中在單執行器控制性能上，沒有同步性的要求。目前關于高精度同步控制的研究則集中于交叉耦合控制器上，這類控制器中應用最多的為PD耦合控制器，這種控制器結構簡單，但魯棒性差，往往需要借助其他控制器以保證系統穩定，參數設置不合理時會直接導致系統的發散，系統存在明顯擾動時同步性能也不佳[12-14]。

因此本文針對隨動壓邊裝置高精度位置控制及高同步性要求，提出了一種基于擾動觀測器的自適應滑模同步控制方法。該方法利用擾動觀測器對未知擾動及未建模量進行預測和補償；通過交叉耦合的方式將同步誤差引入滑模面設計中，以期達到同時降低單液壓缸位置誤差、雙液壓缸同步誤差以及保證系統魯棒性的目的；為提高控制器收斂速度，降低系統抖振，提出一種新的自適應趨近律，以進一步改善控制器的控制輸出。

1 隨動壓邊裝置特性分析

1.1 系統描述

隨動壓邊裝置主要作用為抑制旋壓過程中板坯邊緣“褶皺”等加工失效問題，該裝置能夠在旋壓加工過程中貼著容易發生失效的坯料邊緣，隨著加工過程不斷調整壓邊半徑及自身高度，在“褶皺”等缺陷發生前對其進行外力抑制。

1.上壓邊圈 2.下壓邊圈 3.壓邊滾子 4.液壓馬達 5.下壓邊圈導向柱 6.上壓邊圈導向柱 7.上壓邊圈驅動液壓缸 8.下壓邊圈驅動液壓缸圖1 并聯旋壓機隨動壓邊裝置結構簡圖

本文所討論的隨動壓邊裝置由上、下壓邊圈組成，其中單個壓邊圈由四支導向柱導向，由兩只液壓缸進行驅動。工作中通過調整上、下壓邊圈各自的液壓缸活塞桿位移動態調整上、下壓邊圈的高度，使壓邊滾子與板坯間保持2 mm以內的間隙，限制板坯起皺區間，同時防止壓邊裝置過于壓緊板坯而阻礙加工的進行；通過液壓馬達驅動隨動壓邊圈內部齒輪轉動進而驅動32對壓邊滾子組徑向擴張或者回縮以改變壓邊直徑。所設計的并聯旋壓機隨動壓邊裝置的基本結構簡圖如圖1所示。

隨動壓邊裝置采用液壓驅動。為防止各執行器間的交叉干擾、保持壓力穩定，每個液壓驅動缸均單獨配備比例換向閥和減壓閥，上下壓邊圈液壓驅動缸分別由兩臺液壓泵提供油源，同時為防止壓邊圈失壓下墜，液壓缸各支路均配有液壓單向閥。壓邊裝置電液比例位置控制系統原理圖如圖2所示。

1.液壓驅動缸 2.單向閥 3.比例換向閥 4.減壓閥圖2 壓邊裝置電液比例位置控制系統原理圖

由于上、下隨動壓邊圈要達到的控制效果相同，因此本文將以上隨動壓邊圈組件及其兩只驅動液壓缸作為研究對象進行同步控制算法的設計與控制性能研究。

1.2 系統數學模型

電液比例方向閥是隨動壓邊裝置電液比例位置控制系統的控制元件，通過控制閥的開口大小進而控制流量。第i個電液比例方向閥的閥口輸出流量方程如式(1)所示，其中i取值1、2，代表兩個電液比例方向閥和兩只驅動液壓缸：

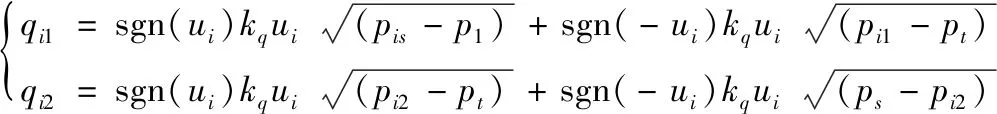
(1)

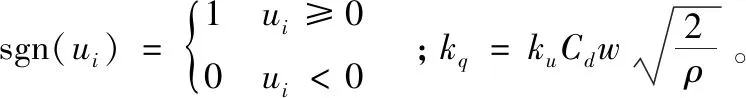
式中，pi1、pi2分別為液壓缸無桿腔和有桿腔的壓力；ps、pt分別為油源壓力和回油壓力；ui為電液比例方向閥的輸入電壓信號；Cd為閥口的流量系數；ku為電液比例方向閥的增益；ρ為液壓油密度；w為電液比例方向閥的閥芯面積梯度。

根據牛頓第二定律，液壓缸活塞上的動力學平衡方程如式(2)所示：

(2)

式中，Ai1、Ai2分別為液壓缸無桿腔和有桿腔的有效作用面積；mi為固定負載質量；xd為活塞位移；Bi為粘性阻尼系數；Fli為理論負載力，該項中包含有壓邊圈重量的偏置部分；di(t)為未知負載擾動。

在合理前提下忽略管道壓損、液壓缸外泄漏，并假定液壓缸腔內壓力處處相等、缸內油溫和體積彈性模量均保持恒定，可以得到液壓缸的流量連續性方程如式(3)所示：

(3)

式中，Ci為內泄漏系數；Vi01、Vi02分別為液壓缸無桿腔和有桿腔初始體積；β為液壓油體積彈性模量。

取系統狀態變量如式(4)所示：

(4)

根據式(1)～式(4)可以建立電液比例位置控制系統的狀態空間方程，如式(5)所示：

(5)

由于活塞桿摩擦、褶皺反力及其他擾動因素的存在，要精確地建立電液比例位置控制系統的數學模型十分困難，因此需要探索一種控制系統的設計方法，能夠進行模型未知項的補償，增強系統魯棒性，并提高系統響應速度以及同步性能。

2 同步控制器設計

2.1 非線性干擾觀測器設計

電液比例位置控制系統的一大特點為干擾難以直接測定。工程上可以通過設計擾動觀測器，利用其他可測物理量對擾動進行預測，從而實現對原系統模型的補償，降低擾動項和未建模項的影響，輔助后續控制器的設計[15-16]。

利用式(2)改寫擾動的估計形式可得式(6)：

(6)

定義擾動估計誤差如式(7)所示：

(7)

假設1：擾動di(t)對時間的導數有界。

擾動觀測器的基本思想是利用擾動估計誤差修正估計值，因此根據假設1可令：

(8)

式中，l0為觀測器線性增益，恒為正。

根據式(6)中呈現出的未知擾動與狀態變量xi2的非線性關系，可在擾動觀測器的設計中引入與狀態變量x2相關的非線性增益項以提高動態性能，定義非線性擾動觀測器如下：

(9)

式中，z為輔助狀態量；l1為觀測器非線性增益，且有：

l1=-mil0

(10)

2.2 滑模同步控制器設計

隨動壓邊圈與兩對稱布置的驅動液壓缸固定連接。考慮到極端工況下，單缸出現故障時控制器仍應能夠輔助保證執行器的同步，防止出現兩缸動作嚴重偏差造成的卡位現象，本文在同步控制策略的選擇上采用交叉耦合的方式，使同步誤差能夠同時對兩缸產生影響。在控制器設計上將同步誤差作為補償項引入滑模控制器，滿足系統的位置控制精度要求的同時，保證系統的同步穩定及魯棒性。

令左右驅動液壓缸的位移誤差分別為e1、e2；位置同步誤差為es；則有：

(11)

式中，x11、x21分別為左右驅動液壓缸的實際位移輸出；xd為期望位移輸出。

以單側驅動液壓缸為例，取如下耦合滑模面：

(12)

式中，c1，c2，w1，w2均為正實數，其值共同決定滑模的動態品質。

設計等速趨近律：

(13)

式中，ε、k均大于0。

根據式(5)、式(12)、式(13)可得：

(14)

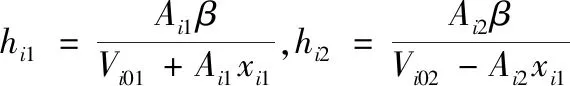
聯立式(8)、式(9)、式(14)可得計算輸入控制電壓ui為：

(15)

式中，usw為切換控制項，當系統產生非線性擾動時，該控制項能夠根據測量誤差及擾動估計值；ueq為狀態控制項，與液壓缸本身狀態相關；uc為耦合補償控制項，與雙缸位置同步誤差相關，其中w1，w2若設為0，則同步控制器退化為單缸控制器，將失去同步誤差補償的效果。

2.3 滑模趨近律改進

通過本文2.2節設計的滑模同步控制器包含了滑模控制的基本特征，等速趨近律下滑模面趨近速度和抖振幅度由參數ε決定：ε取值大，則系統趨近滑模面的時間短，但抖振較大；反之則反。為使系統能夠更快趨近滑模面并且減小滑模抖振，本文提出一種自適應滑模趨近律。

(16)

式中，ρ、ai、as、k、γ均為大于0常數；σ為0～1之間常數。

結合式(14)、式(16)可知，ε恒為正，且當系統狀態遠離滑模面，即s趨于無窮時，ε趨于k|si|，此時系統狀態將指數收斂趨近滑模面；而當系統狀態靠近滑模面，即s趨于0時，ε趨于ρet/(1+et)，此時滑模面的抖振與常數ρ、第i號液壓缸位置誤差ei以及雙缸位置同步誤差es相關，進一步當et趨于0時，ε亦趨于0，從而抖振得到抑制。

2.4 控制器穩定性分析

對于本文設計的同步控制器，發揮性能的前提是擾動觀測器能夠正確起到補償作用。故先選取一個半正定的Lyapunov函數：

(17)

則其導數為：

(18)

式中，λ為任意正數，此時只要滿足l0≧λ/2，擾動觀測器的估計誤差將會指數收斂到原點附近的圓形區域，該誤差由λ，l0，δ共同決定[17]。

繼而定義一個基于式(17)的正定增廣Lyapunov函數：

(19)

對于后半部分的V1，根據本文2.3節，顯然有：

(20)

因此本文設計的同步控制系統是穩定的。

3 仿真實驗分析

為了測試上節設計的同步控制器的控制效果。本文基于Matlab/Simulink設計控制器，并以隨動壓邊裝置上壓邊圈作為控制對象進行仿真分析。完整的電液比例同步控制系統框圖如圖3所示。

圖3 壓邊裝置電液比例同步控制系統框圖

電液比例控制系統的相關基本參數及控制參數如表1所示。

表1 相關液壓參數及控制參數

需要注意的是表1中參數m為壓邊圈整體質量，當兩缸同步誤差很小時，由兩缸位置偏置帶來的偏心質量可忽略不計，各液壓缸所受理論負載近似為整體理論負載的一半，但為了體現同步控制器對于不同末端執行器的同步補償作用，仿真中采取左右頂升缸的理論負載為偏載形式，配比為4:3。

為驗證本文所設計自適應滑模同步控制器的一般性，仿真采用正弦函數作為期望位置函數，該期望函數設置為xd=0.2sin(0.4πt)；對左驅動液壓缸1施加正弦函數擾動，擾動函數設置為d=2000sin(0.8πt)；對右驅動液壓缸2施加固定擾動，擾動大小設置為d=1000 N。

在所設工況下，本文所設計的非線性擾動觀測器估計擾動曲線與實際擾動曲線如圖4所示。從圖4中可以看出擾動觀測器能夠準確地估計系統存在的負載擾動，且能夠快速完成收斂。

(a) 左驅動液壓缸1擾動觀測器 (b) 右驅動液壓缸2擾動觀測器 圖4 估計擾動與實際擾動曲線

上壓邊裝置兩驅動液壓缸位置誤差曲線及兩缸同步位置誤差曲線如圖5所示。其中左右驅動液壓缸的單缸位置誤差在經過0.7 s左右的自我調整后均穩定保持在-0.84～0.68 mm內，兩缸同步位置誤差保持在±1.24×10-3mm以內，這表明該控制器理論上能夠實現快速而準確的同步位置控制，在持續擾動作用下仍然具有較高的魯棒性。

(a) 驅動液壓缸位置跟蹤誤差 (b) 兩缸位置同步誤差 圖5 自適應滑模同步控制器仿真結果

為進一步展現本文同步控制器的性能，本文設置三組對照控制器，分別對擾動觀測器、自適應趨近律、同步控制器的作用以及滑模同步控制器相較于傳統PD耦合控制器的優勢做出分析。

對照組1為無擾動補償的滑模控制器+并行控制；對照組2為有擾動補償的滑模控制器+并行控制；對照組3為有擾動補償的傳統滑模同步控制器+PD耦合控制。各對照組左驅動液壓缸1的位置跟蹤誤差及兩缸間位置同步誤差如圖6所示。

(a) 各對照組左驅動液壓缸1位置跟蹤誤差 (b) 各對照組位置同步誤差 圖6 各對照組控制器仿真結果

根據對照組1與對照組2的仿真結果：當在傳統滑模控制中添加了擾動補償項時，單缸位置跟蹤精度提高了64.13%，且兩缸同步誤差也得到減小。說明添加擾動觀測器后能夠顯著提高該系統的控制精度。

根據對照組2與對比組3的仿真結果：由于耦合控制器的同步誤差補償作用，對比組3的單缸位置跟蹤誤差略微高于對比組2，但其兩缸同步誤差得到顯著的降低。說明如果被控系統對執行器同步性要求高，同步控制器的引入能夠直接且顯著地改善系統的同步性能。

根據對照組3和本文控制器的仿真結果：PD耦合控制器下的兩缸同步位置誤差為±2.51×10-3mm，約為自適應滑模同步控制器雙缸位置同步誤差的兩倍。進一步觀察由耦合控制項引起的控制電壓變化，發現本文同步控制器的同步補償項電壓輸出與PD耦合控制器同步補償電壓輸出如圖7所示。由圖7可以看出本文同步控制器具有更小同步誤差的同時，同步補償項電壓輸出相較于PD耦合控制器的補償電壓輸出更為平滑，因而具有更佳的工程意義。

同時本文同步控制器在收斂時間及抖振幅度上的表現也優于各對照組，進一步證明了本文引入自適應趨近律的有效性。

(a) 滑模同步控制器同步補償項 電壓輸出 (b) PD耦合控制器同步補償項 電壓輸出圖7 同步補償項控制電壓輸出變化

4 結論

為解決并聯旋壓機隨動壓邊裝置的同步位置控制問題，建立了相應的電液比例控制系統數學模型；設計了一種非線性擾動觀測器，用于估計及補償系統中的未知擾動和未建模量；基于擾動觀測器設計了一種滑模同步控制器，并為之設計了自適應趨近律。仿真結果表明該控制器在未知擾動下仍然具有良好的控制性能，相較于傳統滑模控制器能夠更快收斂，抖振更小并且具有更高的位置控制精度；同時這種將同步誤差引入滑模面的方法在減小同步誤差的同時，能夠一定程度上改善控制器同步補償項控制電壓輸出，具有良好的工程實際意義。