基于NMPC的仿人攀爬機器人運動優化*

馬 斌

(重慶工商大學機械工程學院，重慶 400067)

0 引言

機器人不僅在工業領域得到了廣泛的認可，而且在人類生活領域也發揮著重要作用。人形機器人的形狀類似人類，因此它們對人類較為友好，可以使用為人類設計的系統。這是人形機器人被期望積極參與人類生活空間的原因之一[1]。為了在這樣的生活空間中成功地工作，人形機器人必須能夠表現得與人類相似。由于這個原因，人形機器人的行走和奔跑運動已經得到了深入的研究[2]。攀爬運動的控制方法也可以潛在地應用于崎嶇地形環境下的運動。

攀爬墻體是通過在肢體和地形特征之間產生接觸力來完成的，例如突出物、洞和裂縫，這些統稱為“支撐物”。以往的方法需要兩個步驟才能完成爬升運動[3]。在第一步中，確定仿人機器人的可能路徑。在第二步中，確定肢體跟蹤路徑所需的運動。Almonacid M等提出的路徑規劃方法[4]，首先探索每個肢體適用的支撐物組合，然后尋找從開始到目標的一系列可行的支撐物組合。接著在考慮機械約束的同時，生成肢體軌跡以遵循上一步中找到的路徑。換言之，傳統的控制方法一步一步地分別產生路徑和運動。因此，不能實現攀爬運動的整體優化以最大化攀爬效率。

為解決這一問題，本文提出了一種控制方法，能夠同時優化攀爬路徑和運動，使攀爬運動變得更加流暢、實時性更高。將仿人機器人的攀爬任務視為一個考慮機械約束的NMPC問題[5]，并使用基于墻體圖的狀態相關權重和勢函數。在現有方法中，當墻體的信息發生變化(例如檢測到新的支撐物)時，機器人必須停止爬升并生成新的路徑[6]。相比之下，在提出的方法中，如果計算速度足夠高，則可以實時處理墻體信息的變化。但是，使用具有多個支撐的復雜墻體模型來計算控制輸入需要花費大量的時間。因此，為了減少計算成本，還提出了一種視距評估方法，以便從所有可用的信息中選擇必要的信息。

1 系統建模

1.1 仿人機器人模型

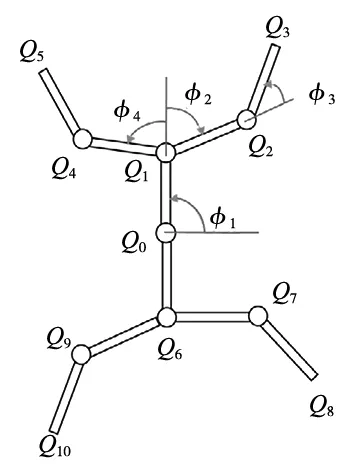
圖1 十自由度連桿 仿人機器人模型

研究采用了一個在垂直平面上具有10個自由度和10個連桿的機器人模型，如圖1所示。假設機器人僅在垂直平面上移動得足夠慢。因此，只考慮運動學模型而不考慮動力學模型。每個連桿的端坐標用Qi=(Qi,x，Qi,y)表示。并且機器人的右手、左手、右腳和左腳的端點坐標分別表示為q1、q2、q3和q4=(Q3、Q5、Q8和Q10)。正方向定義為逆時針方向[7]。相對角度矢量φ定義為：

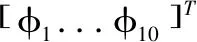
(1)

式中，φi為與根連桿的相對角度。但是，φ1和φ2是從水平軸到Q0的相對角度。將連桿i的坐標系到絕對坐標系的齊次變換矩陣定義為Ti(φ,Q0)。

(2)

式中，Q0為連接桿件1和6的關節坐標，且被定義為機器人的中心；Qi為每個連桿的端點坐標；φ為相對姿態角；li為連桿i的長度；mi為連桿i的重量。機器人中心和每個肢體末端的垂直速度表示為：

(3)

機器人在保持平衡的同時，通過每個關節和手動致動器在支撐物上產生支撐力和扭矩來攀爬力和扭矩的平衡方程[8]表示如下:

(4)

(5)

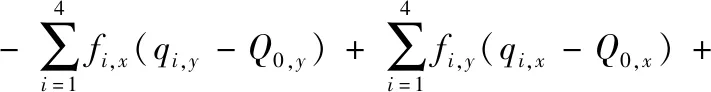
(6)

式中，g為重力加速度；Qg,i為每個連桿的質心坐標，。fi,x為每個肢體qi(i=1,...,4)端點在水平方向上的支撐力；fi,y為每個肢體qi(i=1,...,4)端點在垂直方向上的支撐力；τi為每個肢體qi(i=1,...,4)的端點產生的扭矩。

1.2 墻體模型

假設墻體是垂直平面，并將其設置為xy平面。y軸正方向被視為垂直正方向。假設當每條肢體的端點處于保持狀態(支撐物上)時，機器人可以產生夾持力。墻體上每個點(x,y)在y軸方向上可以產生的最大夾持力表示為：

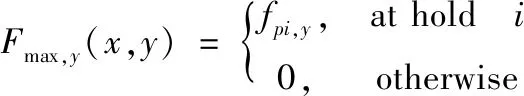
(7)

式中，fpi,y為在支撐i處沿y軸方向可以產生的最大夾持力，其坐標點是(xi,yi)。我們稱這個函數為最大夾持力函數。圖2給出了該函數的一個示例。類似地，在支撐i處x軸方向的最大夾持力和最大扭矩分別由fpi,x和τpi表示。還考慮了最大持力函數Fmax,x(x,y)和Tmax(x,y)。

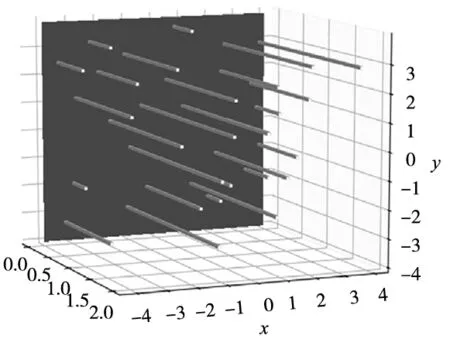
圖2 最大夾持力函數

2 提出的控制方法

2.1 非線性模型預測控制

本文采用實時最優控制中的NMPC來處理非線性的、有約束的控制問題。Kayode owa等[5]對NMPC的多種應用案例有詳細的解釋說明。Yu M等[9]已經考慮了將攀爬任務定義為NMPC的基本思想，但是其設置非常簡單。而在本文將對基于NMPC的仿人攀爬機器人運動進行更加詳細的分析。

在NMPC中，非線性系統的狀態描述方程為：

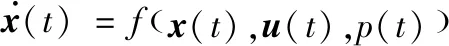
(8)

式中，x(t)為狀態向量，u(t)為輸入向量，p(t)為給定時變參數。考慮從當前時間t到有限未來時間t+T的性能指標J。NMPC中最優控制輸入為uopt(t)(t≤τ≤t+T)，同時考慮如下約束條件：

C(x(τ),u(τ),p(τ))=0

(9)

可見最優控制輸入uopt(τ)取決于當前時間t和狀態x(t)，因此，它可以表示為uopt(τ;t,x(t))。將最優控制輸入的初始值用作時間t處的實際控制輸入。

u(t)=uopt(t;t,x(t))

(10)

這樣，在每個采樣時間，通過求解直到有限未來的最優控制問題來計算控制輸入。采用Continuation/GMRES算法作為實時數值優化方法實現求解線性方程組。對于NMPC來說，只要計算成本不是太高，任何求解大規模非對稱稀疏線性方程組的最常用方法都可以應用到該問題中。

2.2 控制模型

為了讓人形機器人使用NMPC實現攀爬運動，設狀態x為：

(11)

且設輸入u為：

(12)

式中，f為夾持力；d為偽輸入集合，由偽輸入di(i=1,...,12)組成。

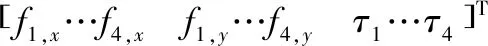
(13)

然后，狀態方程表示為：

(14)

由每個肢體qi端點產生的夾持力fi,x、fi,y和扭矩τi的約束條件為：

-fmaxi,x≤fi,x≤fmaxi,x

(15)

-fmaxi,y≤fi,y≤fmaxi,y

(16)

-τmaxi≤τi≤τmaxi

(17)

其中，

fmaxi,x=Fmax,x(qi)

(18)

fmaxi,y=Fmax,y(qi)

(19)

τmaxi=Tmax(qi)

(20)

可以使用偽輸入di將上述方程轉換為如下情況：

(21)

(22)

(23)

上述3個方程和方程(4)～方程(6)是NMPC中的約束條件。

2.3 路徑和運動的綜合優化方法

(1)性能指標：攀爬性能指標J表示如下：

(24)

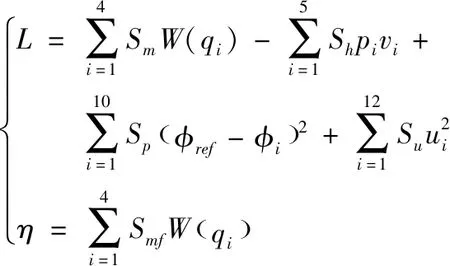
(25)

式中，Sm,Sh,Sp,Su,Sd,Smf為權重；W為勢函數；pi為變權重；φref為參考姿態角。L(x(τ),u(τ))和η(x(t+T))的第一項通過勢函數W引導機器人的肢體攀爬，這將在本節后面解釋。L(x(τ),u(τ))L(x(τ),u(τ))的第二項中變權重pi定義為:

(26)

式中，vref為目標爬升速度。pi代表了每個肢體的實際位置和目標位置之間的差異。例如，如果肢體長時間停留在一個保持狀態，pi值會增加，因此該肢體會被引導到y軸正方向。L中第一項和第二項之間的大小變化，會導致在夾住一個支撐和釋放另一個支撐之間的切換，并提示應該選擇哪些肢體釋放它們的支撐。L的第三項穩定機器人的姿勢，第四項使輸入變小。L的第五項確保偽輸入是正的[10]。通過引入這一項，可以唯一地確定滿足約束條件(式(21)～式(23))的解(fi,di)。

(2)最大夾持力函數：公式(7)中定義的函數Fmax,x(x,y)、Fmax,y(x,y)和Tmax(x,y)是不連續的。NMPC數值優化中不連續函數的處理比較困難，因此將最大持力函數近似化為以下提出的連續函數：

(27)

(28)

(29)

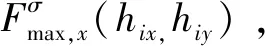
為了滿足上述兩個目標，引入了兩個新參數：σJ和σC。在每個肢體產生的夾持力最大值fmaxi,x,fmaxi,y、扭矩最大值τmaxi以及勢函數W表示如下：

(30)

(31)

(32)

(33)

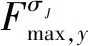
(3)視距評估：如果墻體上有許多支撐，則最大持力函數(式(27)～式(29))會導致相當高的計算成本。這是因為隨著支撐數量的增加，最大保持力函數變得復雜。為了避免這個問題，引入了視距評估。

假設NMPC的時域長度小于從當前時間到機器人完成攀登的時間長度。在這種情況下，運動只能預測和優化到特定的未來時間。因此，即使使用所有的墻體信息來優化運動，其中一些信息也不會影響最優解。此外，由于NMPC本身是一種計算量大的控制方法，因此很難將視界長度延長到機器人完成攀爬的時間。注意到，即使在有限的信息范圍內，也可以根據所有的墻體信息計算出控制輸入。這個范圍被定義為“視距”范圍。除了時域長度外，它還取決于模型的狀態或參數。在本研究中，以機器人的中心坐標Q0、速度v和相對姿態角φ作為確定視距評估的參數。這樣，通過減少需要評估的信息量來減少計算時間。

為了將支撐限制在視距范圍內，將式(28)～式(29)中的最大夾持力函數替換為：

(34)

(35)

(36)

式中，I為由視距范圍內的支撐組成的評估集。從定義來看，I?H。讓視距范圍成為以機器人Q0為中心的圓形范圍。評估半徑由該圓的半徑表示。兩種墻體模型如圖3所示。左邊的例子是式(27)～式(29)中最大夾持力函數的一個示例，它用連續函數來近似。右邊的是式(34)～式(36)中最大保持力函數的一個示例，它僅限于視距范圍。

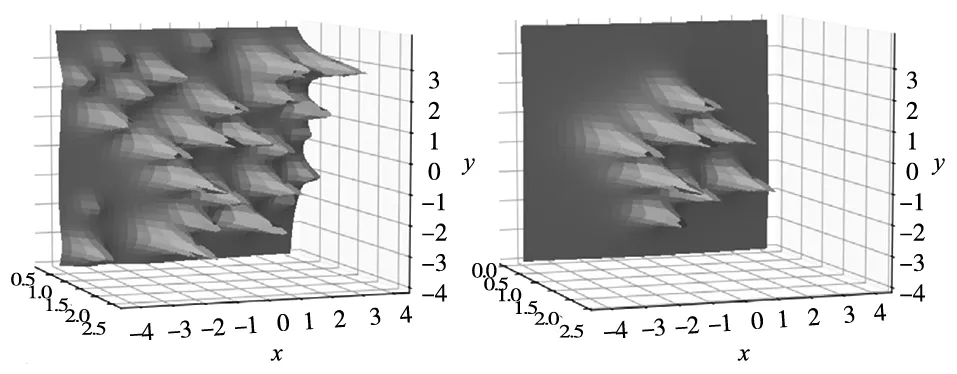
(a) 具有連續函數的墻體模型 (b) 具有視距范圍的墻體模型圖3 墻體模型

隨著函數的變化，在每個肢體產生的夾持力最大值fmaxi,x,fmaxi,y、扭矩最大值τmaxi以及勢函數W替換如下：

(37)

(38)

(39)

(40)

3 實驗及結果分析

3.1 仿真設置

利用計算機數學軟件Maple，在Visual Studio 14.0編譯環境中使用C語言對提出的控制方法進行了機器人行為模擬。

表1列出了與機器人相關的參數。這些參數都是無量綱的。機器人在仿真開始時的初始姿態如表2所示，此時機器人是靜止的，機器人的中心坐標Q0位于原點(0,0)。假設此姿勢為穩定姿勢，則性能指標中參考姿勢角φref的值將設置為與初始姿勢角度相同的值。與墻體相關的參數如表3所示，與性能指標相關的參數(例如權重)如表4所示。

表1 機器人參數

表2 初始姿勢參數

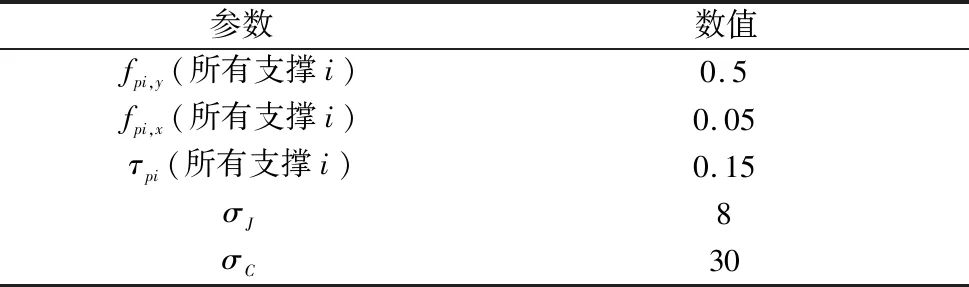
表3 墻體參數

表4 性能指標參數

初始姿態和支撐布置情況如圖4中Time0所示。仿真的計算條件如表5所示，參考了文獻[10]的設置經驗。

圖4 攀爬行為結果(Case 4)

表5 仿真的計算條件

3.2 仿真結果

從圖4可以看出，機器人能夠根據墻體信息實現支撐選擇和爬墻支撐切換，驗證了提出控制方法的可行性。Case 1、Case 2、Case 3和Case 4更新一次控制輸入的計算時間分別為12.4、15.2、18.5和19.5 ms。這些結果表明，隨著評估半徑的減小，計算時間也隨之減少。這是因為用于仿真的墻體信息量隨著評估半徑的減少而減少。

3.3 真實案例測試

選擇近藤公司的KHR-3HV型仿人機器人對提出控制方法進行了實際攀爬測試。該仿人機器人沒有特殊的抓握機構，而是采用角托架作為手，符合本文模型設定。此外，設計了一個攀爬的簡易墻體，由多孔木墻制成。支撐物是由金屬環制成的。同仿真實驗一致，也使用了不同的評估半徑來執行仿人攀爬機器人行為控制。同仿真一樣，圖5給出了Case 4的實際行為結果。每個Case均執行10次并取平均獲得攀爬全過程的時間。結果顯示，Case 1、Case 2、Case 3和Case 4的時間排序與仿真結果一致。相比于Case 4(154 s)，Case 1(97.9 s)的攀爬時間減少了36.4%，驗證了提出控制方法的有效性。

圖5 實測攀爬行為結果

4 結論

本文提出了一種基于NMPC的仿人機器人攀爬控制方法。該方法能夠在考慮機械約束的情況下實現路徑和運動的綜合優化，并通過使用視距評估在線配置性能指標來減少計算時間。與將墻體上的所有支撐都納入視距范圍的情況相比，攀爬時間減少了36.4%。使用狀態相關權重的性能指標不僅可以應用于機器人的攀爬控制，還可以應用于其他NMPC問題。此外，該視距評估方法還可以應用于具有復雜環境下的機器人或者車輛控制問題。但是，真實實驗中每種Case的計算時間都略長于控制輸入的更新周期。后續將考慮使用高性能的計算機或開發一種新的方法來更有效地確定評估范圍以便解決這個問題。