基于結構權重的三維模型動態約簡方法的研究*

歐陽會東，吳文江，胡 毅

(1.中國科學院大學，北京 100049 ；2.中國科學院沈陽計算技術研究所，沈陽 110168 ；3.沈陽高精數控智能技術股份有限公司，沈陽 110168)

0 引言

隨著“中國制造2025”和“工業4.0”在國內的提出，工業生產的數字化建設也愈發重要。近年來，虛擬現實、數字孿生等技術的迅速發展也為數字化建設提供了強大的技術支持[1-3]。計算機硬件水平雖然在高速的發展，但是虛擬三維模型的渲染速度也在隨著用戶對模型精度的要求的提高越來越無法滿足需要。針對3D場景中模型的渲染，國內外學者提出了很多不同的解決方法，如細節層次模型LOD(Level of Detail)技術，基于GPU的渲染加速技術等[4-6]。上述方法雖然較大的提升了模型的渲染速度，但是上述方法都是對三維模型的整體進行渲染。針對復雜度高，子結構較多的三維模型，仍然存在渲染速度過慢，GPU和內存占用率過高的問題。

本文通過研究三維模型的結構特征，發現三維模型在不同的視點距離下，部分結構的渲染對模型整體真實度的影響較小，這部分模型結構對模型整體真實度的影響因子很低。根據模型子結構相對于模型整體的體積比例不同，隨著視點與模型的距離變化，可以動態的計算各個子結構的渲染度，通過與渲染閾值進行比較，可以避免對影響因子較低的結構進行渲染。該方法可以較為明顯的減小三維模型的渲染壓力。能夠在不影響模型整體真實度的情況下，提高模型的渲染速度，降低GPU和內存的占用率。

1 三維模型結構的權重系數的確定

本文是根據三維模型與視點的距離，確定不同結構的渲染程度。各個結構的權重系數可以通過以下3步進行確定：

(1)確定主要模型結構：主要模型結構為三維模型的暴露在視點范圍內的結構。針對這部分結構，賦予較大的權重系數，即使模型與視點的距離很大，也能保證視點范圍內模型的整體真實度。

(2)確定次要模型結構：次要的模型結構為不暴露在視點范圍內的結構。這部分結構的渲染度會跟隨視點距離模型的遠近不斷改變，從而動態的對模型結構進行約簡。

(3)針對每一個模型結構相對于模型整體的的體積比，賦予模型結構不同的權重系數。當視點與模型的距離非常遠的時候，細小的模型結構的渲染對模型整體的影響將會變得很小，此時可以放棄這部分結構的渲染，從而節省系統資源，提高渲染速度。

2 動態約簡方法的實現

動態約簡的實現主要分為三個方面：首先計算模型結構相對于整體的體積比，然后判斷模型結構是否在視點范圍內，并計算視點與模型之間的距離，最后計算模型結構的渲染度，通過渲染度與渲染閾值的比較，判斷當前結構是否需要進行渲染，實現渲染過程中對模型結構的動態約簡。

2.1 計算三維模型結構的體積

Unity3d引擎中，每一個模型都有MeshFilter組件，MeshFilter組件中又包含了Mesh屬性。Mesh屬性中記錄了vertices(頂點數據數組)、triangles(三角形頂點索引數組)、normals(法線向量數組)、uv(紋理坐標數組)等信息。針對每一個模型都有MeshFilter(網格過濾器)屬性。

圖1 三維立方體模型圖

為了計算三維模型的體積，首先我們需要取得三維模型所有頂點及三角面片的數據，Unity3d中提供了mesh.vertices以及mesh.triangle兩個屬性，分別為vector3型數組和int型數組。其中mesh.vertices存儲的就是平面的頂點信息，mesh.triangles存儲的是三角形的頂點繪制順序。然后將計算的代碼腳本掛載于需要計算體積的模型結構上。以一個三維立方體為例，如圖1所示。

首先通過mesh.vertices獲取當前模型的三角面片所有頂點順序，然后根據渲染順序計算每三個連續繪制頂點與中心坐標點組合而成的三棱錐的體積。Unity3d引擎中，每個模型自身的中心坐標點為(0,0,0)，假設三棱錐的三個連續繪制頂點坐標為分別為(x1,y1,z1)，(x2,y2,z2)，(x3,y3,z3)。根據坐標向量即可通過行列式計算三棱錐的體積，即空間坐標系中的三棱錐的體積計算公式如下所示：

(1)

最后統計所有三棱錐的體積之和，即可以得到當前三維模型結構的體積。

2.2 視點范圍的判斷方法

Unity3d引擎中，與視點范圍相關的坐標系分別為視口坐標系與世界坐標系。視口坐標系用于描述整個渲染畫面的坐標，左下角為(0,0)，右上角為(1,1)。世界坐標系為整個渲染場景的坐標系，可以通過transform.position()函數獲取。為了判斷模型是否在視點范圍內，首先需要判斷當前模型在視窗的坐標是否在視口坐標系的范圍類，然后通過點積運算判斷模型是否在攝像機的前面，最后根據上述的計算結構即可確定模型結構是否在視點的范圍內，詳細的流程如圖2所示。

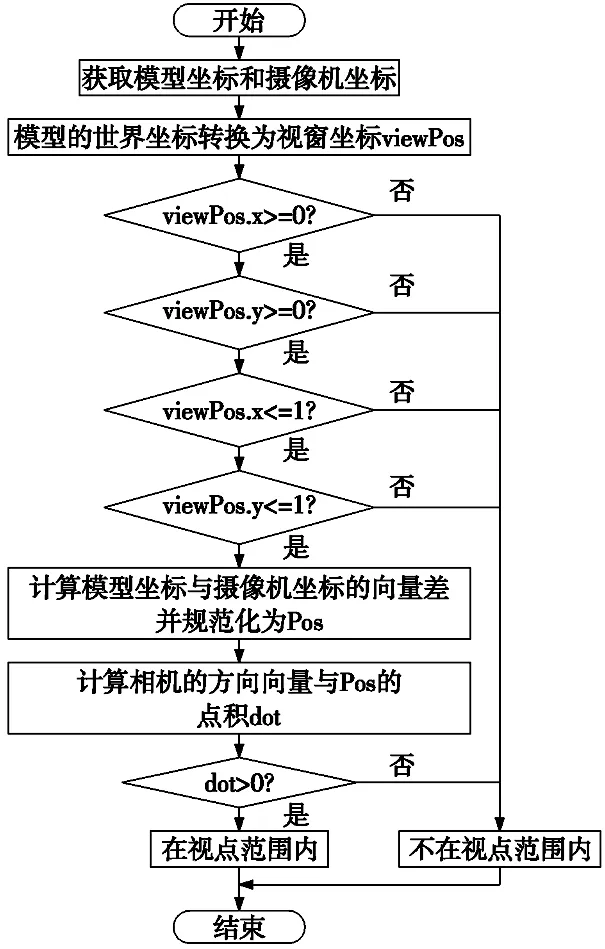
圖2 視點范圍判斷流程圖

2.3 視點與模型之間的距離

本文主要通過Unity3d軟件進行研究及實驗。距離的計算采用的是Unity3d軟件自帶的Vector3.Distance函數，調用該函數可以計算出視點與模型之間的距離L(單位為m)，函數偽代碼如下：

float L=Vector3.Distance(transform1.position, transform2.position)

2.4 渲染度計算

本文算法在判斷三維模型的某個結構是否渲染主要考慮兩個因素，一個是該結構的體積Vi，另一個是視點與該模型之間的距離L，通過以上因素提出了渲染度以及渲染閾值的概念 。其中渲染度S定義公式為：

(2)

其中，當前模型結構在視點范圍內時P的值為1，否則為0，σ為視點范圍內模型結構的權重系數。ρ為體積占比的權重系數。

針對每一個三維模型，設置一個渲染閾值M，并通過 Renderer.enabled 屬性控制其渲染。根據公式(1)計算該結構的渲染度。當結構渲染度小于閾值的時候，該結構在通過腳本控制取消渲染。只有結構的渲染度大于或等于渲染閾值的時候，腳本才將其渲染出來。根據不同計算機的硬件條件，可以設置不同精度的σ和ρ，σ和ρ越大，渲染的模型精度越高，隨著距離的增大，渲染的模型結構數量越多。也可以宏觀的調節渲染閾值M的值，對所有模型結構的渲染進行統一控制。

3 實驗分析

3.1 實驗環境

實驗主要工具為Unity3d軟件，硬件配置如表1所示。

表1 硬件配置表

3.2 實驗過程與結果

為了驗證基于三維模型結構權重的動態約簡方法，使用不同三角面片數量的模型進行實驗，下圖為采用的實驗模型示意圖，其中圖3為實驗所用的模型結構透視圖，圖4為模型實體圖。

圖3 模型結構透視圖

圖4 模型實體圖

該模型總計有547個子結構，216 802個三角面片，通過多次實驗，不斷調整參數的數值，實驗最終設置視點范圍內模型結構的權重系數σ為100，體積的權重系數ρ為1，渲染閾值M為0.75， 然后對模型的結構進行體積計算并賦予相應的權重。通過調整視點與模型的遠近，記錄當前場景中的三角面片數量，幀率以及此時視點與模型之間的距離。表2為記錄的主要實驗數據。

表2 面片數量變化表

為了驗證方法的通用性，同時對三個不同三角面片數量的三維模型進行渲染，并繪制出三角面片數量根據距離的變化的折線圖，如圖5所示。其中縱軸為三角面片數量，橫軸為視點與模型之間的距離 。

圖5 三角面片數量變化折線圖

由折線圖可以觀察到，模型在視點與其距離逐漸增大的過程中，三角面片渲染的數量在逐步降低。并且隨著距離的進一步增大，開始趨向于一個穩定數值，這樣距離過大時也保證了模型在視點范圍內不會消失。

在上述研究的基礎上，將該方法應用到虛擬現實場景中。通過對比試驗論證該方法的實用性，并繪制距離與FPS(畫面每秒傳輸幀數)的變化圖。其中實驗1為不使用三維模型動態約簡方法，實驗2使用了三維模型動態約簡方法。

圖6 實驗結果對比圖

實驗結果顯示，三維模型動態約簡方法的應用，大幅度提升了虛擬現實場景渲染的流暢度，隨著視點與三維場景的距離的增加，系統整體的FPS不斷在上升并逐漸趨于穩定。其中使用了三維模型動態約簡方法的實驗2的FPS隨著距離的增加一直高于未使用該方法的實驗1。

4 結論

虛擬現實、數字孿生等技術一直是很多國內外學者研究的重點。三維模型作為這些技術的基礎，針對三維模型的簡化也有很多不同的方法。本文提出了基于模型結構權重的三維模型動態約簡方法，該方法首先計算了模型結構的體積，模型結構與視點之間的距離，并判斷當前模型結構是否在視點范圍內，然后通過渲染度公式計算每個模型結構渲染度，最后通過渲染度與渲染閾值的比較，通過腳本控制當前模型結構的渲染。 該方法針對復雜的三維模型以及大型三維場景的實時渲染，在保證模型真實性的前提下，大幅度減少了三角面片的渲染數量，提高了模型的渲染速度，保證了三維場景渲染的流暢度，通過對比實驗，在距離達到100 m以上時，三維場景的渲染幀率有了顯著提升。 同時本文所提出的渲染度公式中加入了人工調整的控制參數，針對不同硬件配置的機器，調整不同的參數大小，保證了硬件配置較低的計算機同樣可以快速渲染模型及三維場景，賦予了該方法更多的靈活性與適用范圍。