基于NARX神經網絡的磁流變阻尼器模型研究*

孫 奇，呂宏展

(東華大學機械工程學院，上海 201620)

0 引言

磁流變液作為一種智能材料，具有良好的可控性、響應速度快、并且在一定溫度范圍內工作較為穩定，因此可以被用來作為磁流變阻尼器內部的可流變阻尼材料，在汽車懸架[1]、橋梁減震[2]和仿生假肢[3]等領域得到了廣泛的應用。在前期文獻中，由于磁流變阻尼發生過程中伴隨的非線性滯回力學行為，給力學模型對阻尼力學行為的精確描述帶來了一定的挑戰。隨著阻尼器件對控制精度的要求越來越高，因此，建立精確的磁流變阻尼器力學模型是實現對磁流變阻尼器高精度控制的前提和基礎，也使得磁流變阻尼模型的建模一直是國內外學者關注與研究的熱點問題。Occhiuzzi A等[4]利用Bingham模型擬合最大阻尼力為50 kN的磁流變阻尼器，經過比較后發現Bingham模型對高電流水平下的阻尼力-位移曲線擬合效果較差，周強等[5]提出改進的Bingham模型，改進的方式是在原Bingham的基礎上串聯一個彈簧元件，該模型能夠擬合阻尼力-位移曲線，但對阻尼力-速度曲線在低速區無法做到非線性擬合。Sims N D等[6]提出雙粘性模型，通過建立前屈服參數、后屈服參數、屈服力和外部激勵條件之間的經驗形狀關系完成建模。Li W H等[7]根據磁流變液在屈服前為粘彈性體，屈服后階段為粘塑性體兩種狀態提出粘彈性-塑性模型，對處于兩個階段的狀態分別建立控制方程，然后通過參數識別求解方程參數，但該模型在阻尼力-速度曲線中也無法做到非線性擬合。Spencer B F等[8]提出改進的Bouc-Wen模型，該模型能夠有效地擬合磁流變阻尼力的力學特性，但該模型存在14個參數，使得該模型比較復雜。

本文以磁流變阻尼器在不同輸入電流情況下阻尼器產生的阻尼力、阻尼器活塞桿的位移和速度等實驗數據為基礎，提出一種基于NARX神經網絡的磁流變阻尼器模型。闡述NARX神經網絡的基本原理，并分析模型中串-并行結構和并行結構的特點及作用，最終將NARX神經網絡模型得到的仿真結果與實驗結果進行比較，驗證所提出的模型是否可行有效。

1 磁流變阻尼器力學性能實驗

1.1 實驗測試平臺

圖1 TPW-D2型微機控制電子式減震實驗平臺

實驗采用的測試平臺是TPW-D2型微機控制電子式減振器，整個實驗平臺如圖1所示，在阻尼器安裝位置的下端為輪輻式負荷傳感器，負荷傳感器與磁流變阻尼器的安裝和夾緊裝置相連接，用來測量阻尼器產生的阻尼力，伺服電機內部的光電編碼器用來實時檢測推桿的直線位移。

圖2 RD-8040-1磁流變阻尼器

測試的阻尼器選用美國某公司生產的單筒式小型磁流變阻尼器，如圖2所示，該阻尼器的型號為RD-8040-1，該類型的磁流變阻尼器在變化磁場的作用下其響應的時間不超過15 ms，使用較為簡單并且擁有長期的穩定性。該阻尼器最大的輸入電流值為1 A，但通電時間不能連續超過30 s，間歇性的通電最大電流值為2.0 A，工作時最高溫度不能超過71 °C，在正常工作溫度下，其電阻為5 Ω，71 °C時電阻為7 Ω，阻尼器的內部安裝了高壓氮氣囊，壓強為300 psi。型號為RD-8040-1的磁流變阻尼器行程為55 mm，阻尼器總長為208 mm，阻尼器的圓筒直徑為42.1 mm，活塞桿直徑為10 mm。

1.2 實驗結果與分析

實驗將磁流變阻尼器分別輸入0.15 A、0.20 A、0.25 A和0.30 A的電流，在每一個不同的輸入電流下，均采用正弦激勵信號驅動磁流變阻尼器做上下運動，振幅值均為8 mm，進行4次不同電流值的分組實驗。 通過對磁流變阻尼器施加4次不同電流值的實驗得到的阻尼力-位移和阻尼力-速度曲線分別如圖3、圖4所示。

圖3 阻尼力-位移(0.15 A～0.30 A)

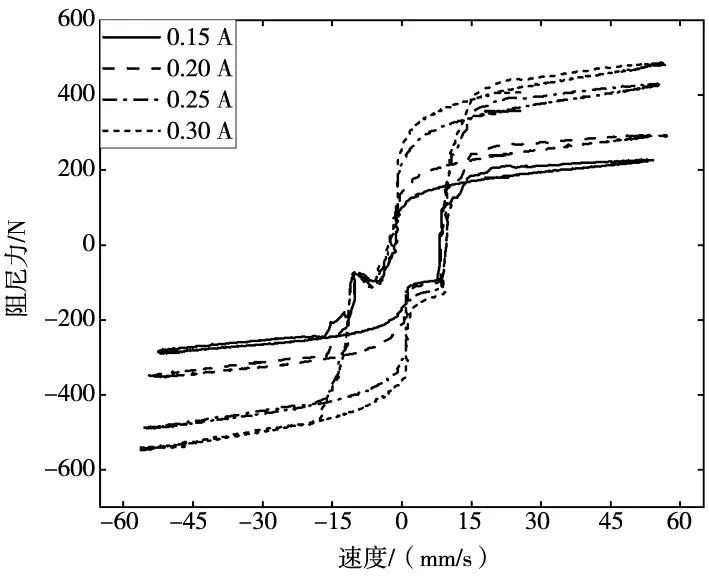
圖4 阻尼力-速度(0.15 A～0.30 A)

可以看出，圖3中阻尼力與位移為一種矩形環狀關系，而且阻尼力的峰值隨著電流值的增大而增大；圖4中阻尼力-速度曲線圖的低速區可以發現，阻尼力與速度表現出明顯的非線性及滯回特性，并且滯回環的面積隨著電流值的增大而增加，在高速區，阻尼力與速度呈現一種簡單的線性關系。所以，評價一個模型擬合精度的高低關鍵在于能否精確擬合阻尼力-速度曲線在低速區的非線性及滯回特性。Bingham模型和雙粘性模型在高速區和低速區都只是線性擬合，無法做到非線性擬合，而且也不能表現出滯回特性，導致這兩個模型都不能精確地描述阻尼力-速度曲線低速滯回行為[9]。雙粘性滯回模型雖然能夠在低速區表現出滯回特性，但也無法做到非線性擬合，因此雙粘性模型的擬合精度也具有一定的局限性[10]。神經網絡在理論上能夠以比較高的精度擬合任意復雜的非線性曲線，而且不需要知道要擬合對象的數學模型，因此這里擬采用神經網絡算法來進行阻尼力-速度曲線的描述與建模工作。

2 NARX神經網絡力學模型

2.1 NARX神經網絡原理

NARX神經網絡是一種帶有外部輸入的非線性自回歸神經網絡，其特點在于輸入層設定有延遲階數，這種結構也稱之為時間延遲神經網絡。此外，NARX神經網絡存在輸出反饋，即從神經網絡的輸出層反饋回輸入層，在NARX神經網絡中，將帶有輸出反饋的結構稱為并行結構，無輸出反饋則稱為串-并行結構。這里的反饋是將串-并行結構訓練得到輸出值反饋給輸入層代替真實的輸出值以此來計算神經網絡的輸出。串-并行結構用來訓練神經網絡，并行結構用來計算神經網絡的輸出結果。對于NARX神經網絡模型，模型中輸入與輸出的映射關系為[11]：

(1)

圖5 NARX神經網絡串-并行結構

圖6 NARX神經網絡并行結構

2.2 訓練算法

(2)

(3)

(4)

(5)

其中，σ表示輸出層的傳遞函數。

對于誤差反向回傳算法，設多組輸入輸出對為{(p1,t1),(p2,t2),…,(pQ,tQ)}，損失函數為：

(6)

tq表示目標輸出值，yq表示NARX神經網絡的計算輸出值，對于輸入層與隱藏層的權值變化量，其表達式為：

(7)

(8)

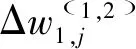
(9)

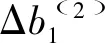
(10)

該誤差回傳算法的不足之處在于學習率的選取問題，目前還沒有較為成熟的理論來指導如何選取學習率，學習率α是一個大于0的正值，如果對學習率選取的太小，那么神經網絡的各個參數變化量將很小，此時，梯度下降的速度很慢，這會增加神經網絡的訓練時間；如果學習率取的太大，那么很可能得不到損失函數的極小值，甚至會處于發散狀態。此外，學習率α是一個固定值，一旦選定則在訓練過程中無法改變，因此，該算法不具備自我調節能力，需要對此進行改進。文中采用了基于Levenberg-Marquardt的誤差回傳算法，設神經網絡的性能函數為：

(11)

基于Levenberg-Marquardt算法的表達式為[12]：

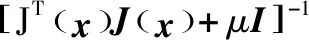
(12)

2.3 訓練結果及評價

本文將數據樣本劃分為訓練數據集、驗證數據集和測試數據集三部分，各個數據集占總數據集的比例分別為70%、15%和15%，并采用隨機劃分的方式劃分三部分數據集，使得數據集之間不存在數據重疊和交叉，保證數據劃分的合理性。

當完成實驗的數據劃分和神經網絡訓練后，三部分數據集及總體數據集回歸圖如圖7所示，圖中回歸值R表示訓練的輸出值與目標值的擬合精度，R的數值越接近于1，則輸出值與目標值的擬合精度越高，R的數值越接近于0，則輸出值與目標值的擬合精度越低。從圖中可以看出，訓練數據集、驗證數據集、測試數據集和總體數據集對應的R值分別為0.999 91、0.999 97、0.999 94和0.999 92，4個R值的結果均接近于1，這說明NARX神經網絡模型有非常高的訓練精度。

圖7 神經網絡訓練回歸圖

為了能夠更加直觀地觀察到神經網絡訓練得到是輸出值與目標值的誤差大小，圖8表示總體數據樣本點對應的誤差及實際的擬合曲線，其中輸出值表示神經網絡訓練得到的阻尼力，目標值表示實驗測量的阻尼力。從圖中可以看出，三部分數據集對阻尼力的峰值擬合精度較高，而對于阻尼力變化幅度大的區域擬合精度較低，對應下面誤差圖中誤差較大，但誤差較大的數據樣本點僅占總體數據樣本點的0.87 %，證明神經網絡的訓練達到了理想效果。

圖8 總體數據樣本誤差

3 模型驗證

為驗證前述模型的精度及可靠性，通過實驗測試重新獲得實驗樣本數據，將獲得的樣本數據輸入到神經網絡模型中，模型的輸入值分別為活塞桿的位移、速度和輸入電流，輸出值為阻尼力，即該網絡模型是一種多輸入單輸出模型。當在串-并行結構中訓練結束后，將串-并行結構轉換為并行結構，最后在NARX神經網絡模型的并行結構中計算輸出阻尼力，圖9和圖10分別是電流值為0.15 A、0.20 A、0.25 A和0.30 A實驗結果與模型計算結果對應的阻尼力-位移曲線圖和阻尼力-速度曲線圖。

圖9 實驗結果與模型結果(阻尼力-位移)

圖10 實驗結果與模型結果(阻尼力-速度)

通過對比實驗結果和NARX神經網絡模型的計算結果可知，NARX神經網絡模型對阻尼力-位移曲線和阻尼力-速度曲線均有較好的吻合。為了能夠定量地描述模型對不同電流值下的擬合精度，采用阻尼力的相對誤差來表示模型與實驗的誤差，在不同電流值下的阻尼力相對誤差圖柱狀圖如圖11所示，從圖11可以發現，電流值在0.15 A～0.3 A對應的相對誤差分別為3.77%、3.23%、2.1%和1.99%，即電流值為0.30 A的相對誤差最小，其值為1.99%，電流值為0.15 A的相對誤差最大，其值為3.77%。從相對誤差這一指標可以證明該模型對電流值為0.30 A的擬合精度最高，對電流值為0.15 A的擬合精度最低，模型中最大的相對誤差不到4%，該結果在一定程度上驗證了文中所提出的模型在描述低速區域非線性滯回問題方面是有效的。

圖11 相對誤差柱狀圖

4 結論

(1) 本文對磁流變阻尼器進行四次不同電流值的實驗并分析了實驗結果，結果表明磁流變阻尼器工作在低速區時，表現出明顯的非線性滯回特性；此外，隨著施加電流強度的增大，阻尼力的峰值及在低速區滯回環的面積也逐漸增大。

(2) 提出一種基于NARX神經網絡的磁流變阻尼器模型，該模型利用串-并聯結構訓練神經網絡，之后將串-并聯結構轉化為并聯結構計算模型的輸出結果。通過比較試驗結果與模型結果發現，在勵磁電流較大時(0.3 A),阻尼力最小的相對誤差僅為1.99%；在勵磁電流較小時(0.15 A)，阻尼力輸出的最大相對誤差為3.77%，該模型輸出結果誤差水平低于當前其他模型的水平，對磁流變低速區域的滯回行為描述精度較高。

(3) 相比于參數化模型，NARX神經網絡不需要對磁流變液在屈服前和屈服后作出假設，只要給出擬合對象的輸入和輸出就能夠做到高精度擬合；通過觀察實驗結果與模型結果的擬合效果及阻尼力的相對誤差驗證了NARX神經網絡能夠做到以較高的精度擬合磁流變阻尼器的非線性及滯回特性。