基于MATLAB回歸分析在礦區通風粉塵排放預測中的研究

梁 敏

(天地科技股份有限公司，北京 100013)

可持續發展是當今國際社會的主題，它要求經濟建設和社會發展要與自然承載能力相協調，發展的同時必須保護和改善地球生態環境，保證自然資源和環境成本以可持續的方式使用。

當前，我國發展過程中面臨的突出矛盾之一就是環境污染問題，特別是空氣污染問題尤為嚴重。一般而言，空氣污染主要是由可懸浮顆粒物超標造成的，而粉塵的過量排放是造成可懸浮顆粒物超標的重要原因。煤礦通風排放物中的粉塵是一種重要的大氣污染物，其主要成份是煤炭開采、掘進、運輸過程中產生的巖粉和細微的煤炭顆粒，粉塵排出風井后會對空氣產生污染，危及人類的健康，其在沉降后還會造成周圍土壤的重金屬污染[1]。

我國是礦物生產大國，眾多礦山曾為社會經濟發展提供了重要的物質基礎，同時也造成了大量的環境問題[2]，摸清粉塵排放量及其分布對于粉塵防治具有重要意義[3]。目前，國內缺少對礦井通風粉塵的系統研究，因此，有必要在實地調研的基礎上利用數值分析方法對礦井通風粉塵的排放情況進行分析，從而為通風粉塵的治理提供參考。

1 礦井粉塵排放情況調研

煤礦井下的主要塵源點是采、掘工作面，其產塵量占全礦井的85%以上[4]，井下粉塵經過風井后呈氣流狀排向大氣, 逐漸彌散[5]，其排放量與礦井年產量、總回風量、粉塵濃度等數據密切相關。為了研究它們之間的關系，通過調研測試得到35座礦井的年產量、總回風量、粉塵濃度等數據，使用MATLAB軟件對數據進行處理，建立數據間的函數關系，從而得到礦區煤礦粉塵排放量預測公式。

眾所周知，預測公式能夠使用的重要前提是要有相關變量的準確數據，即預測地區內煤礦的產量、總回風量、粉塵濃度等。一個礦區內的煤礦眾多，由于礦井的總回風量和粉塵濃度數據需經現場測試收集，在計算礦區的通風粉塵排放量時，需對礦區內所有煤礦開展大規模調研測試，可見通過上述兩個數據得到的預測公式在使用時很不方便，同時，礦區的煤炭總產量數據相比于礦井總回風量、粉塵濃度等數據更易獲得。為了簡化問題，使礦區通風粉塵排放量預測公式簡便易用，僅就礦井年產量與粉塵排放量之間的關系開展研究。

為了研究礦井年產量和通風粉塵排放量間的規律，將調研得到的礦井年產量數據作橫坐標，相應的通風粉塵排放量數據作為縱坐標。根據調研測試值，作出數據的散點圖，如圖1所示。

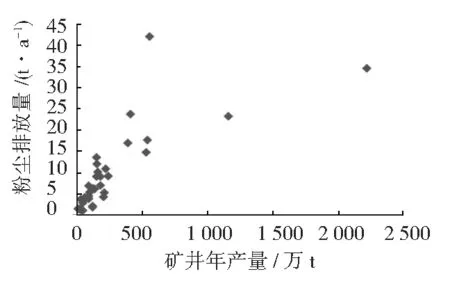
圖1 礦井年產量與通風粉塵排放量數據散點圖

由于散點圖上的大部分數據在一定范圍內呈現線性趨勢，可以使用回歸分析的方法進行數值分析。

2 數據擬合分析

數值分析運用十分廣泛，它可以根據自變量的數值和變化，估計和預測應變量的相應數值和變化[6]。回歸分析是一種常見的數值分析方法，屬于定量分析的范疇[7]。它基于統計觀測數據建立變量間的數學關系，通過分析數據間的內在規律，建立回歸方程，可以確定兩種或兩種以上變量之間的相互依賴關系。按照自變量和因變量之間的關系類型，可分為線性回歸分析和非線性回歸分析；按照涉及的自變量的多少，可分為一元回歸分析和多元回歸分析。在回歸分析中，如果只包括一個自變量和一個因變量，且二者的關系可用一條直線近似表示，這種回歸分析稱為一元線性回歸分析。如果回歸分析中包括兩個或兩個以上的自變量，且因變量和自變量之間是線性關系，則稱為多元線性回歸分析。

2.1 模型建立

礦井年產量和粉塵排放量都是一維變量，而且散點圖中的數據在一定范圍內呈線性趨勢，符合線性回歸模型的構造條件，采用一元線性回歸方法對數據進行擬合。

2.1.1 線性回歸模型

一元線性回歸的數學表達式為：

y=a+bx

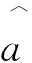
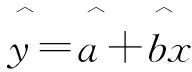
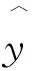
2.1.2 線性回歸檢驗

在得到一元線性回歸模型后，還需對其進行相關度檢驗，常用的檢驗方法有以下兩種：

1)F檢驗。如果x和y有線性關系，則:

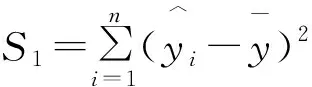
2)t檢驗。檢驗的原假設為：H0∶B1=0。對立假設為：H1∶B1≠0。如果原假設H0成立，表明因變量y與自變量x之間沒有線性關系，即x的變化對y沒有影響，一元線性回歸不成立。如果當H1成立時，則認為自變量x對因變量y的影響顯著，即回歸模型成立。

2.1.3 擬合度分析

相關系數r用來表示自變量和因變量之間線性關系的密切程度，其計算公式為：

當相關系數r為正值時，表示自變量x和因變量y呈正相關；當r為負值時，自變量x和因變量y呈負相關。當r=0時，說明2個量之間無直線關系；當r=±1時，表示數據完全正相關或負相關，此時散點圖上的數據都集中在回歸直線上。通常認為當r的絕對值大于或等于0.75時，自變量和因變量具有很強的線性相關性。

2.2 回歸分析

2.2.1 回歸模型建立

套用一元線性回歸方程建立粉塵排放量預測公式。

令x表示礦井年產量，y表示粉塵排放量，假定x和y有如下關系式：

y=a+bx

利用MATLAB中的regress函數對方程進行求解，對x和y作一元線性回歸分析，從得到的結果看，常數項和回歸系數的估計值分別為4.766 9和0.017 5，回歸系數估計值的95%置信區間為[0.012 2，0.022 9]。

則線性回歸方程可表達為：

y=4.766 9 + 0.017 5x

相關系數R的值為0.574 4，可見礦井年產量和粉塵排放量呈正相關，但由于R<0.75，表面兩者間的線性關系不強。

2.2.2 殘差分析

圖2中的每條豎直線段都對應一組樣本的殘差和殘差的置信區間，線段中點處的圓圈對應縱坐標為殘差值的大小，線段上端點的縱坐標為置信上限，下端點的縱坐標為置信下限。若殘差的置信區間不包括零點，則認為該組數據異常。

通過調用rcoplot函數，做出兩組數據對應的殘差和殘差的置信區間圖，數據對應殘差如圖2所示。通過對殘差和殘差的置信區間的分析，可以看出原始數據中存在的異常數據點。

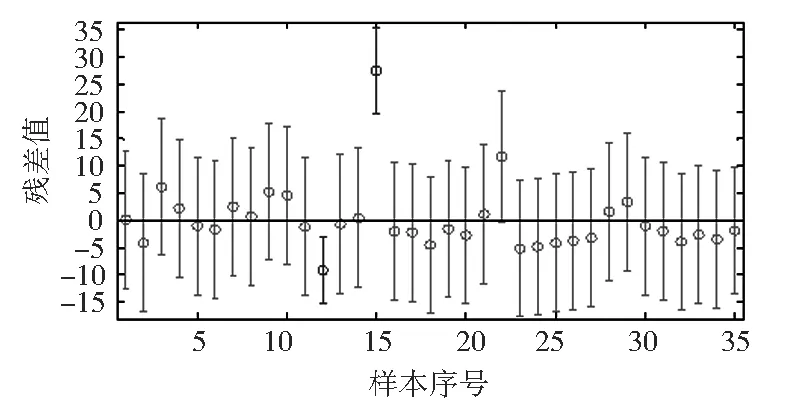
圖2 殘差圖

從殘差圖可以看出：有兩條線段與水平線(y=0)沒有交點，可認為這兩組數據為異常數據。

2.2.3 最優值求解

將異常數據剔除后重新對數據進行擬合，利用MATLAB對余下的數據作線性回歸分析，從得到的結果看，常數項和回歸系數的估計值分別為1.546 8和0.030 3，回歸系數估計值的95%置信區間為[0.024 4，0.036 1]，數據散點與回歸直線圖見圖3，則線性回歸方程可表達為：

y=1.546 8+0.030 3x

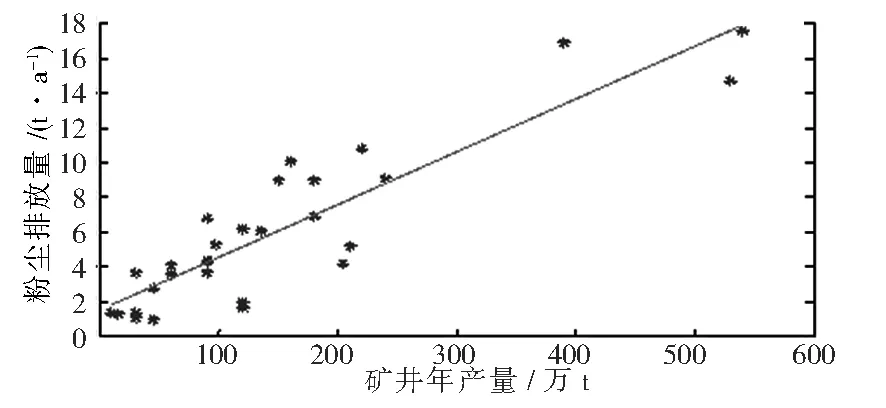
圖3 數據散點與回歸直線圖

相關系數R的值為0.81，通過與上次回歸分析的R值相比較，發現在剔除異常數據后，相關系數的值有了明顯的提高，而且大于0.75，表明兩者間具有很強的線性關系。

從數據散點與回歸直線圖可以看出，散點數據均勻分布在回歸直線兩側，說明數據擬合度較高。

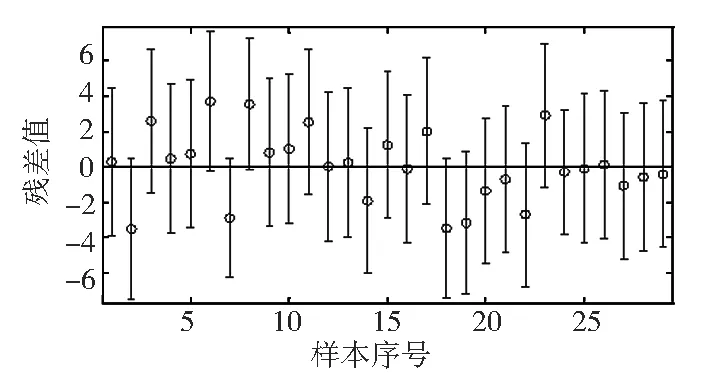
圖4 殘差圖

從圖4可以看出，樣本中已沒有異常數據，即樣本與水平線y=0都存在交點。

3 結 語

1) 調研中絕大多數礦井的通風粉塵排放量與礦井的年產量呈現出一定的關聯性。

2) 以礦井年產量和通風粉塵排放量數據為基礎，建立了線性回歸模型，分別采用MATLAB軟件中的regress函數和rcoplot函數求解回歸值，求解得到的線性回歸方程相關性系數R=0.81，具有較高的可靠性，可用于估算樣本礦區的通風粉塵排放量數據。

3) 數據分析中存在部分異常點，集中在年產量1 000萬t以上的大型礦井，開采方式主要為綜放開采，礦井產量與通風粉塵排放量之間的線性關系較弱，千萬噸級礦井是未來礦井發展的主要方向，對于該類型礦井的通風粉塵排放情況有待進一步的研究分析。