分數階混沌系統動力學特性分析與DSP實現

劉天明，閻慧臻，馬晨光，楊飛飛，曹穎鴻

(大連工業大學 信息科學與工程學院,遼寧 大連 116034)

0 引 言

近年來的分數階微積分的相關研究表明，相比于整數階微積分，分數階微積分可以更好地描述客觀物理世界[1]，因此針對分數階微積分的研究成為熱點。針對Chen系統[2]、Liu系統[3]和簡化Lorenz系統[4]等非線性混沌系統的研究發現，相比于整數階混沌系統，分數階混沌系統具有更為復雜的動力學特性[5-6]。

目前，分數階混沌系統的求解算法主要有頻域法(FDM)[7]、預估校正法(ABM)[8]和Adomian分解法(ADM)[9]。這些算法普遍采用的是黎曼-劉維爾定義和卡普托定義，但它們都存在一些問題：首先是其不能滿足整數階微積分所滿足的一些重要性質[10]，例如乘積法則和鏈式法則；其次，計算過程非常復雜[11-12]。因此，Khalil等[13]提出了一種新的分數微積分定義——可整合分數微積分。該分數階微積分定義和性質與ADM算法相結合可以很好彌補現有算法求解分數階微分方程的不足[14-15]。CADM算法改進ADM算法，降低了計算的復雜程度，并具備較快的收斂速度、計算速度和較小的資源消耗等優點[10]。CADM算法求解分數階混沌系統正逐漸成為研究的熱點[16-18]。

分數階混沌系統的應用[19-21]實際依賴信號處理的軟硬件技術。數字信號處理器(DSP)以其性能優越、處理方便等優點在工程上得到了廣泛的應用。基于此，本研究利用DSP技術，對提出的四維分數階混沌系統進行了硬件實現。

本研究在一個四維Sprott-B混沌系統的基礎上，利用可整合微積分定義構造該四維混沌系統的分數階形式。基于CADM算法求取該分數階系統的數值解，對其動力學行為進行了分析，利用0-1測試驗證產生混沌最小階數，同時用SE和C0復雜度算法分析了該系統隨機性。最后運用DSP技術對該系統進行了硬件實現。

1 分數階混沌系統數值分析

1.1 分數階混沌系統CADM求解算法

設一個分數階系統方程為

(1)

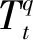
(2)

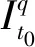
(3)

將系統非線性項進行分解：

(4)

式中：i=0，1，2，…；j=1，2，…。則方程數值解為

(5)

式中：

(6)

1.2 分數階混沌系統求解

在文獻[22]提出的Sprott-B系統的基礎上設計了一個新的四維自治混沌系統如式(7)所示。

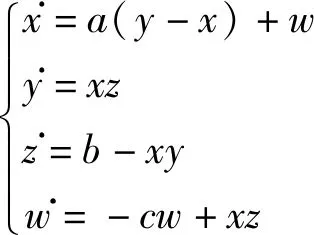
(7)

式中：x，y，z，w為狀態變量；a，b，c為系統參數。

根據分數階微積分定義，式(7)對應的分數階系統為

(8)

式中：q為系統階數。分解式(8)可得其中的線性項、非線性項和常數項分別為

(9)

(10)

(11)

根據式(4)對系統非線性項進行分解，在保證精度的基礎上取前6項可得

(12)

(13)

(14)

設該分數階混沌系統的初值為x0=[x1(0)，x2(0)，x3(0)，x4(0)]，展開式第一項為

(15)

同時令

(16)

(17)

令h=t-t0為步長，同時

(18)

則第二項可表示為

(19)

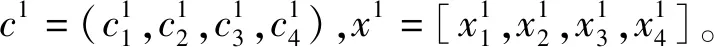
類似地，可得其他5項展開式分別為

(20)

(21)

(22)

(23)

(24)

由此可得此時分數階混沌系統解為

(25)

2 分數階混沌系統動力學特性分析

2.1 系統仿真

取式(7)系統參數a=4、b=9、c=5和q=0.8，步長h=0.01，x0=[1，1，1，1]，系統相圖如圖1所示。此時李雅普諾夫指數為L1=1.017 0、L2=0、L3=-12.547 9和L4=-16.720 6，系統維度DL=2.09。系統有一個正的李雅普諾夫指數，表明此時系統為混沌態。

此時系統Poincaré截面如圖2所示，圖中Poincaré截面既不是有限點集，也不是封閉曲線，是一些成片的具有分形結構的密集點，這種結構具備混沌系統的典型特征。

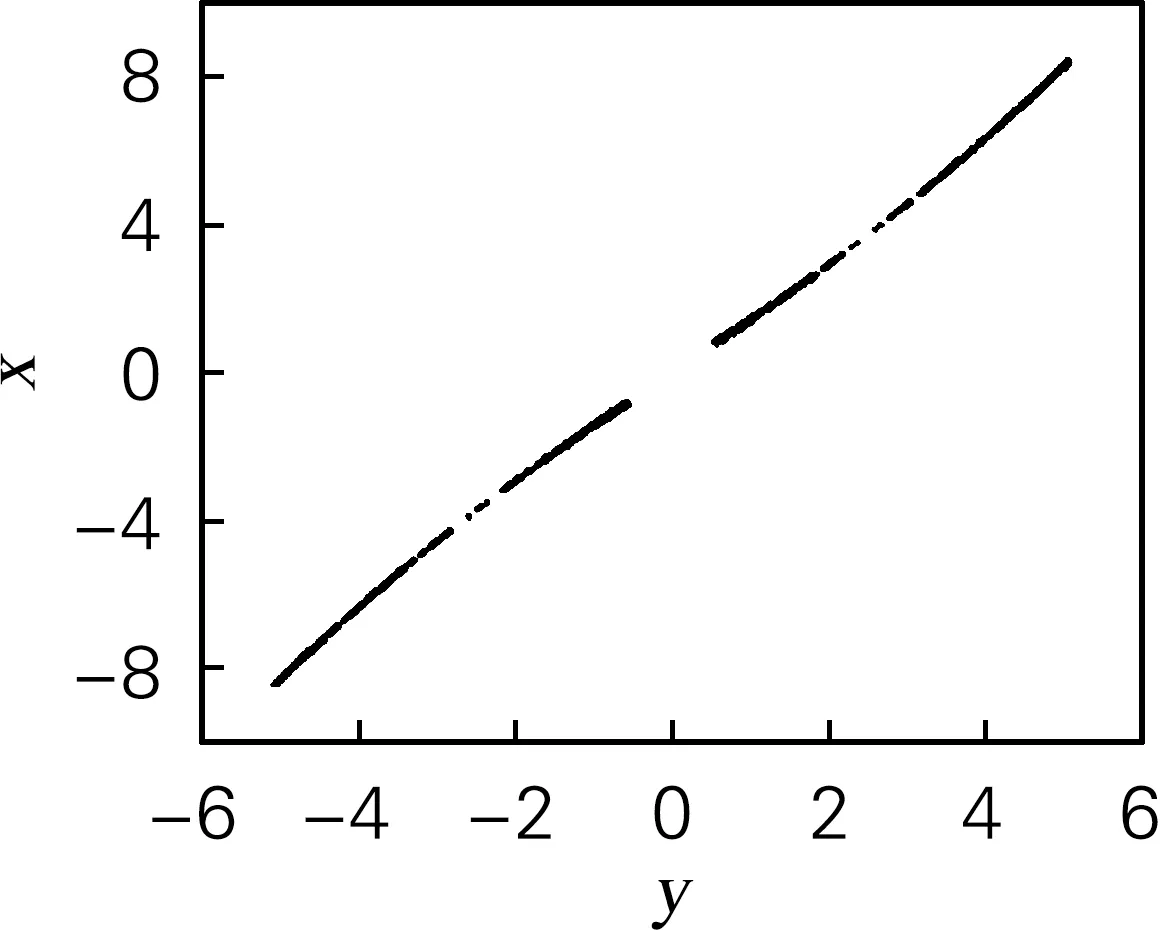
圖2 系統y-x平面的Poincaré截面(q=0.8)Fig.2 Poincaré section of the system on the y-x plane (q=0.8)

2.2 系統穩定性分析

(26)

取a=4、b=9和c=5，此時系統平衡點為S1，2=(±3，±3，0，0)，系統特征方程為

λ32+9λ24+29λ16+126λ8+360=0

(27)

求解特征方程特征值，若其滿足

(28)

則系統在平衡點是漸進穩定的[23]。其中M是分數階分母的最小公倍數。將特征值代入式(28)得

(29)

表明此時系統特征值滿足式(28)，所以系統在平衡點S1，2處是穩定的。

2.3 系統參數變化對動力學特性的影響

2.3.1 參數a對系統動力學特性影響

取參數b=9、c=5和q=0.8，仿真步長h=0.01，系統初值x0=[1，1，1，1]，當a∈[1，5]時，系統的李雅普諾夫指數譜和分岔圖如圖3所示。為了更好觀察系統特性變化，在圖3(a)中舍去了最小的兩條李雅普指數曲線。當a在[2.98，3.03]，[3.46，3.5]，[4.27，4.33]和[4.34，5]范圍內取值時，系統最大的李雅普諾夫指數為零，所以a在這些區間內取值系統是周期態。在其他范圍內，最大的李雅普諾夫指數為正，系統是處于混沌態。表1總結了當系統隨參數a變化時所具有的復雜動力學行為。

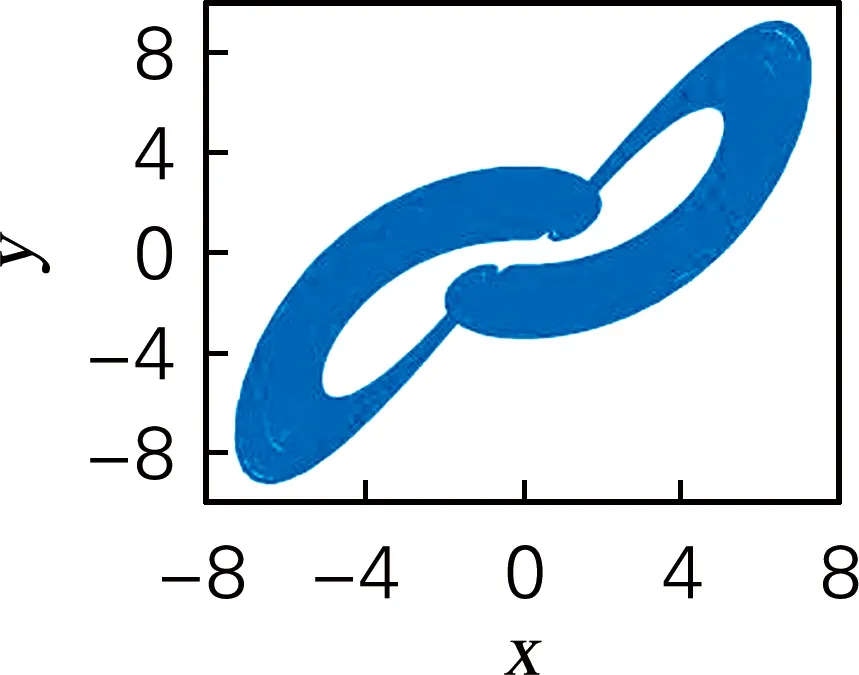
(a) x-y平面相圖

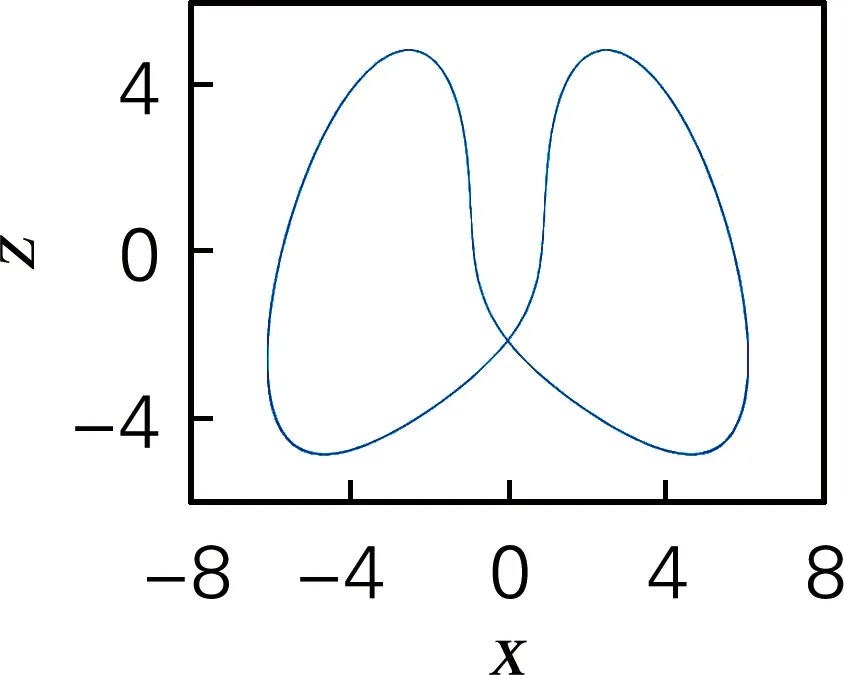
(a) a=5.00

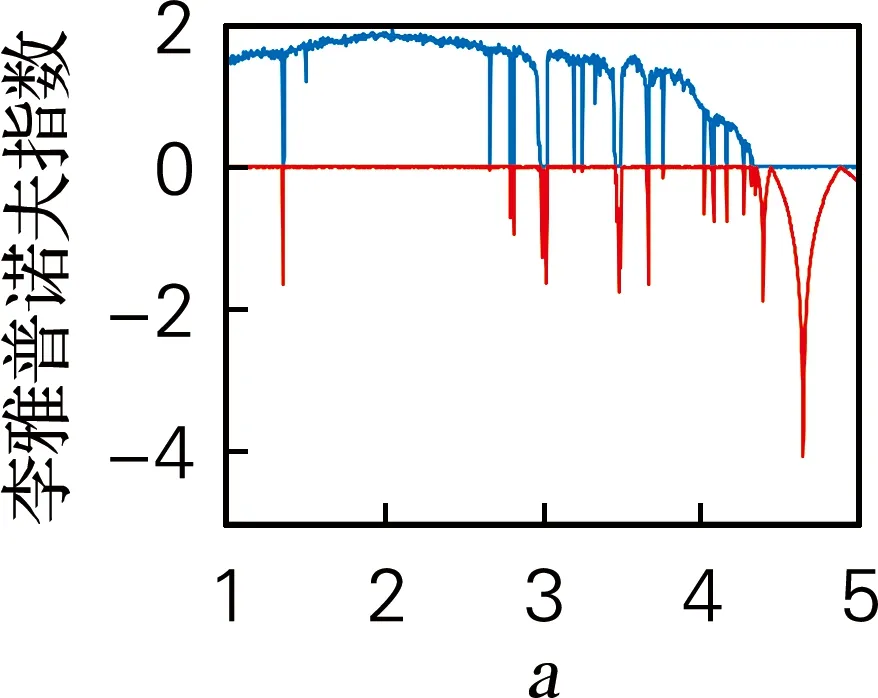
(a) 李雅普諾夫指數譜

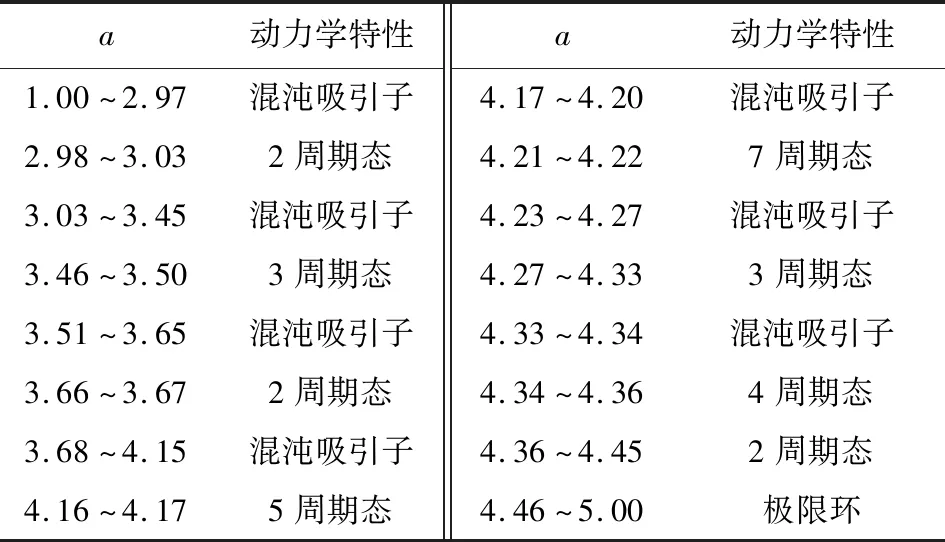
表1 參數a變化的系統狀態Tab.1 The system status with a

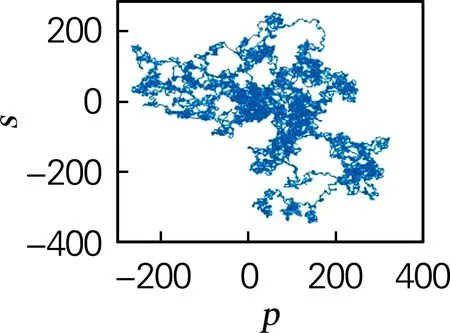
由表1可知，參數a∈[1，5]時，系統中出現了一種典型的混沌吸引子和6種不同類型的周期態。圖4中分別取了周期1(a=5)、周期2(a=4.4)、周期5(a=4.16)和混沌態(a=4)時的相圖和0-1測試，圖中可以看到當系統處于周期態時，p-s平面上是有界的規則的運動；當系統處于混沌態時，p-s平面上是類似于布朗運動的無界運動。

2.3.2 參數b對系統動力學特性影響

取參數a=4、c=5和q=0.8，仿真步長h=0.01，系統初值x0=[1，1，1，1]，圖5是系統參數b∈[7，11]變化時的李雅普諾夫指數譜和分岔圖。圖5(a)同樣舍去最小的兩條李雅普諾夫指數曲線。從分岔圖中可以看到，隨著參數b增加，系統通過倍周期分岔從周期態進入混沌狀態，同時當參數b在[8.53，8.59]和[10.21，10.25]處時出現兩個較為明顯的周期窗口，這與李雅普諾夫指數譜是相對應的。

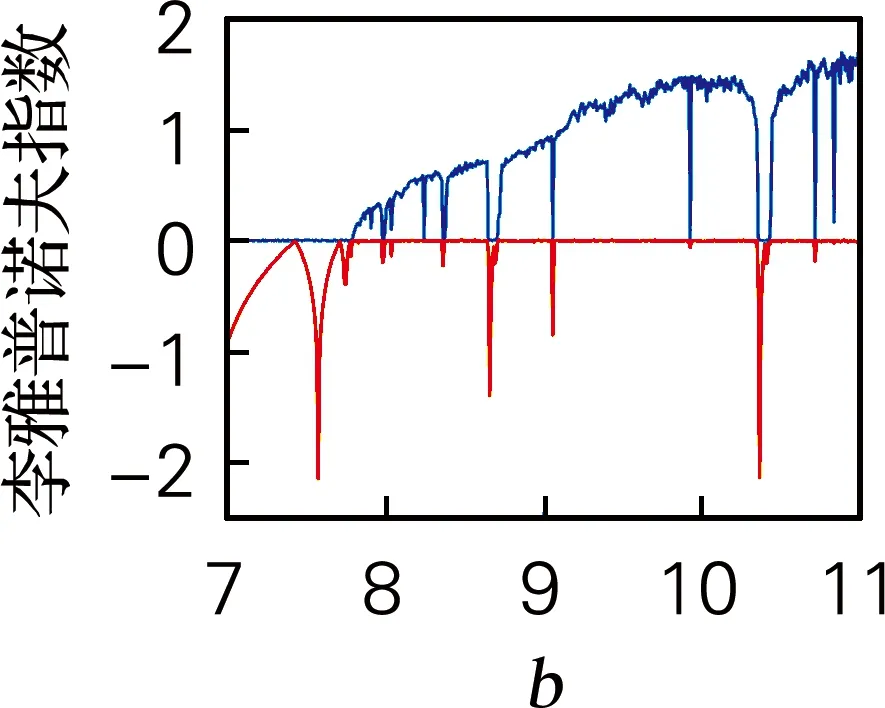
(a) 李雅普諾夫指數譜

如表2所示，系統參數b∈(7，11)時，系統出現了各種不同的動力學行為，有多種類型的周期態和混沌態出現，說明參數b的變化對系統動力學特性有較大的影響。

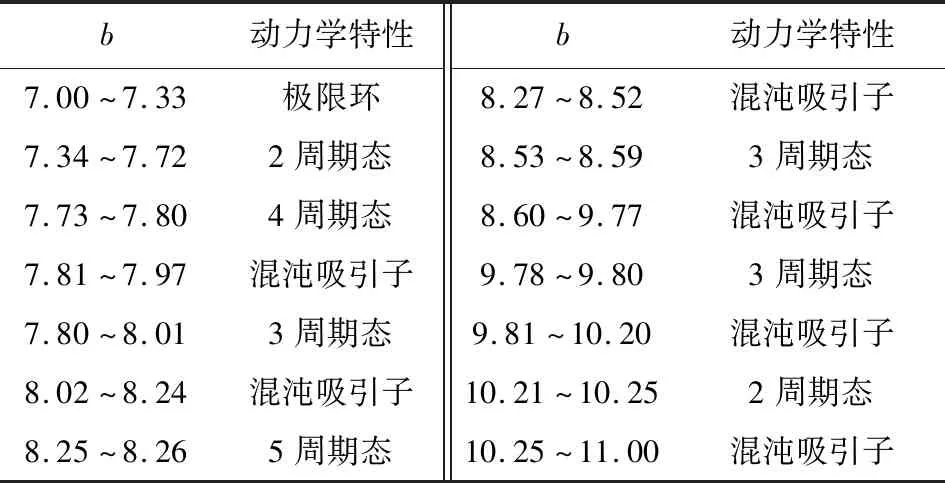
表2 參數b變化的系統狀態Tab.2 The system status with b

2.3.3 階數q對系統動力學特性的研究

取a=4、b=9和c=5，步長h=0.01，系統初值x0=[1，1，1，1]，q∈[0.5，1]。系統隨階數q變化的指數譜和分岔圖如圖6所示。從圖6(a)李雅普諾夫指數譜中可見，當q∈[0.53，1]，系統處于混沌狀態。當q<0.52時，在分岔圖和李雅普諾夫指數譜中均沒有數值，系統處于發散狀態。

(a) q=0.53

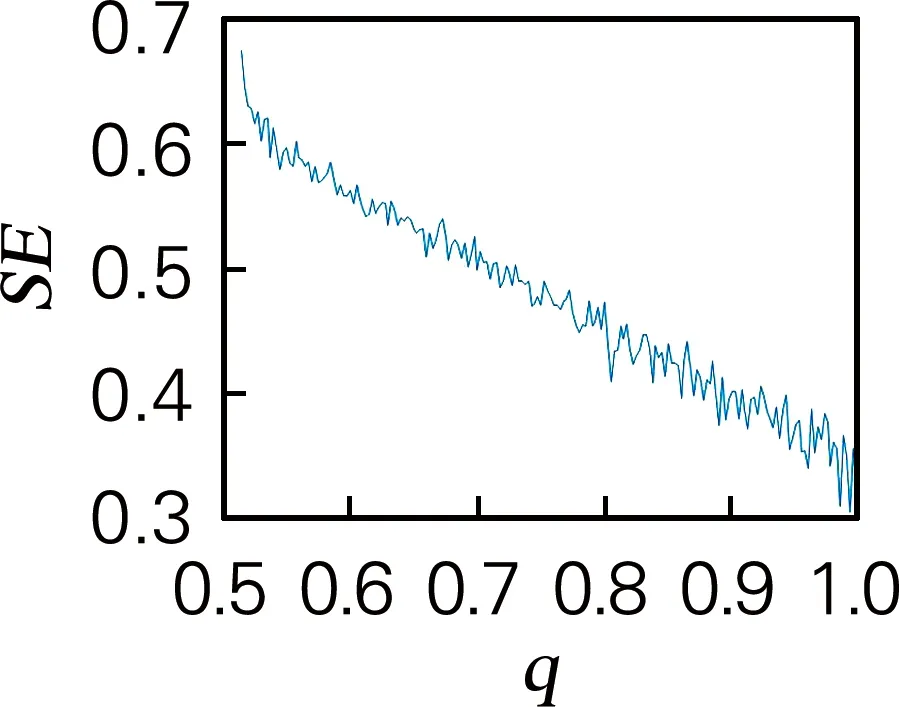
(a) SE復雜度

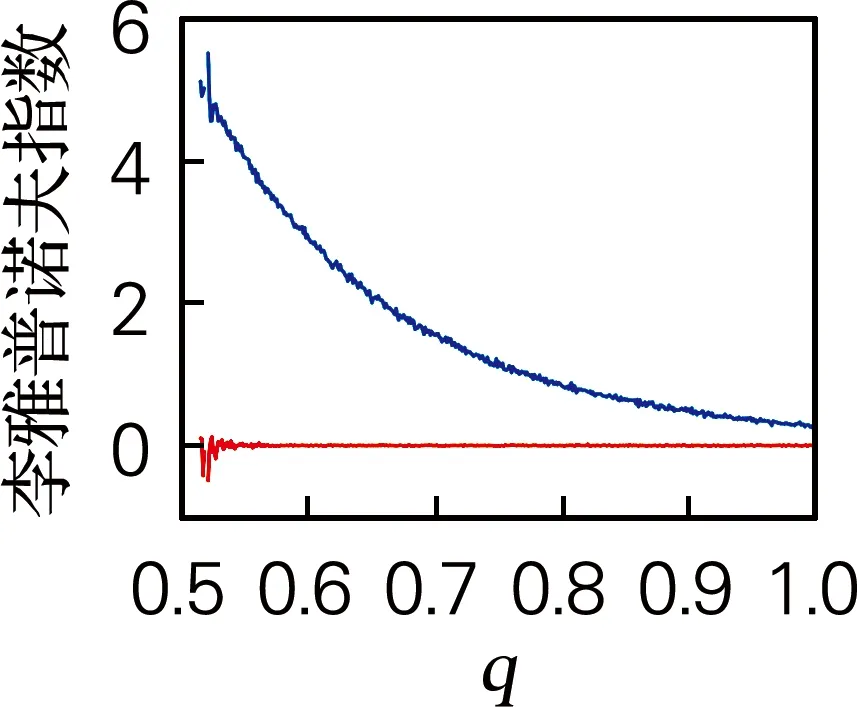
(a) 李雅普諾夫指數譜

為了進一步分析系統適用于保密通信等領域的參數選擇范圍，更好的觀測混沌系統的動力學特性[24-27]。取系統階數q∈(0.5，1)，序列長度N=50 000，此時系統SE復雜度和C0復雜度如圖7所示。由圖(7)知，當q大于0.52時，SE復雜度和C0復雜度的變化趨勢是逐漸減小的，當q=1時，復雜度的值達到最小。可見，分數階混沌系統是比整數階混沌系統更為復雜，隨著階數減小，系統復雜度會相應變大，說明該系統的分數階狀態比整數階狀態具有高的應用價值。

由圖6可知q<0.52時，系統是發散的，為了驗證系統產生混沌的最小階數，引入了0-1測試。0-1測試的結果如圖8所示，當參數q=0.53時，測試結果為類布朗運動，說明系統是混沌的。如圖8(b)所示當參數q=0.52時，測試結果為穩定點，說明系統是非混沌的。由此可得系統產生混沌的最小階數0.53×4=2.12。

3 分數階混沌系統DSP實現

完成分數階混沌系統的硬件實現是其實際應用的基礎。首先對DSP進行初始化，并進行系統初始設置。然后對系統式(8)進行迭代，將迭代結果數據推送入硬件系統后處理并將結果從DSP中輸出，最后使用數據進行初始值的替換并進行迭代，直到結束為止。在數據處理環節，DSP產生的數據被傳送入DAC8552中轉換成模擬信號傳送給示波器。

DSP硬件平臺中采用的DSP-芯片為TMS320F28335，采用16位雙通道D/A轉換器DAC8552對由DSP產生的時間序列進行轉換。D/A轉換器由DSP通過SPI(串行外圍接口)控制，把數字信號轉化為模擬信號傳送到示波器上顯示。

圖9為通過DSP平臺得到的混沌系統信號相圖。此處系統參數a=4、b=9和c=5，系統階數q=0.8，步長h=0.01，將其與計算機仿真得到的系統相圖進行比較，二者結果是一致的。

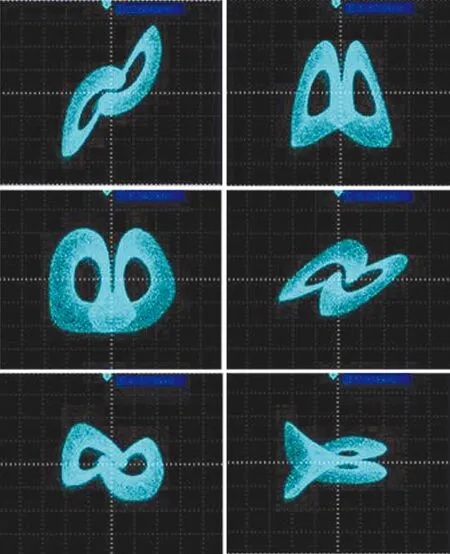
圖9 DSP實現系統相圖Fig.9 The system phase diagram of DSP implementation

4 結 論

設計了一種四維分數階系統，采用CADM分解算法求解了該四維分數階混沌系統的數值解并分析了該系統動力學特性。結果表明，該分數階混沌系統具有復雜的動力學行為。系統產生混沌的最小階數為2.12，而且通過復雜度分析可知，當q=0.53時，系統復雜度最高，此時混沌序列隨機性最好，安全性能最高。最后在DSP平臺上完成了該系統的硬件實現，結果體現了CADM算法的正確性以及分數階混沌系統的物理可實現性。研究結果為分數階混沌系統運用于保密通信等領域，提供了理論和實際應用基礎。