FE-SEA方法在平臺支持船噪聲預報中的應用

辛子豪，樊 紅，鄒郁筱，周瑞平

(1.武漢理工大學 能源與動力工程學院，武漢430063；2.東風商用車技術中心，武漢430056)

平臺支持船是為海上油氣開采和能源利用而建造的輔助船舶，因功能差異有不同類型，但通常都配備有動力定位系統。無論是巡航作業還是海上補給時，側推裝置長時間都處于工作狀態，其產生的噪聲會給船員帶來極大的不適。尤其是艏部側推裝置因位于上層建筑艙室的正下方，成為船舶最主要振聲源[1]。

艙室噪聲預報可以有效幫助人們預估所設計船舶的噪聲水平，目前的數值模擬方法主要有有限元（FE）和統計能量分析（SEA）法。FE 法一般適用于低頻噪聲計算，對于復雜結構系統的高頻噪聲計算，節點與單元數量明顯增加，隨之而來的是計算量和誤差的顯著增大。SEA 法在計算量上有明顯優勢，是解決復雜系統寬帶高頻動力學問題的有力工具。許多學者進行過統計能量法在船舶噪聲預測中的應用研究，驗證了在船體模型建立合理的基礎上，SEA方法的可行性[2-3]。Weryk 等學者[4]在6 艘同系列AHTS（Anchor handling tug supply）船上進行噪聲測量，并將測量值與SEA 方法的預報值進行對比，結果較為吻合，但研究中模擬的是船舶航行工況噪聲情況，并未考慮側推裝置對噪聲的影響。為保證SEA 模型計算的準確性，通常需要模型的子系統達到足夠高的模態密度，而中低頻區的模態數較小，SEA 法的預測結果并不理想。1999年，Langley 和Bremner[5]最先提出了基于模態理論的FE-SEA混合算法，Shorter 和Langley[6-7]于2005年改進了這一算法。Cotoni 和Shorter[8]對比了FE-SEA 法與FE 法計算的動態響應，驗證了FE-SEA 的可行性。隨后，FE-SEA混合法在船舶、汽車和航空航天等領域得到了廣泛應用[9-11]。

本文以某65 m AHTS 船為研究對象，采用CFD方法計算艏側推螺旋槳作用在隧道型導管上的脈動壓力，采用FE-SEA 混合法計算中頻段平臺支持船艙室噪聲，采用SEA 方法計算高頻段噪聲，繼而得到全頻段艙室噪聲。

1 研究對象

本文所研究的AHTS 船除可完成錨操作、離岸平臺拖吊和供應功能外，還兼有油收集和對外消防功能。船舶總長65 m，垂線間長57.3 m，型寬16.8 m，設計吃水5 m。雙機雙槳主推進系統，主機額定功率2 205 kW，額定轉速800 r/min，兩臺AZIMUTH舵槳機。柴油發電機組由四臺450 kW 柴油機驅動交流發電機組成。艏側推柴油機額定功率874 kW，額定轉速1 500 r/min。船艏安裝有兩個側推槳，位于貫通的隧道型導管中，一臺由柴油機驅動，一臺由電機驅動。后部導管軸線位于84號肋位處，距基線高度2 m，管徑2.106 m，兩端呈喇叭口形狀。

2 FE-SEA方法理論概述

對于一個復雜結構系統，其“中頻段”結構組件的模態重疊數差別較大，部分構件顯示出剛性特點，部分顯示為柔性，單一的FE 或SEA 方法都難精確、高效地預報結果。FE-SEA 混合法根據結構特征尺寸與波長間的關系，將分析對象劃分為確定性子系統和隨機性子系統，并根據兩子系統邊界處直接場和混響場的互易關系將它們重新聯系起來，得到整體結構的響應。

確定性子系統的動力學方程[6]可以表示為

式中：Dd為確定性子系統總體動剛度矩陣；q為確定性子系統位移；f 為確定性子系統外激勵力向量；ffuz為隨機性子系統對確定性子系統產生的力向量。

式中：frev為混響場產生的受擋力；fdir為由直接場產生的力向量；Ddir為直接場動剛度矩陣。

由直接場和混響場的互易關系[9]：

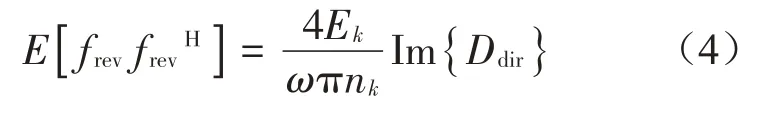
式中：E[·]表示總體平均；下標k 表示第k 個隨機子系統；Ek表示隨機子系統所具有的能量，可由隨機子系統的功率流平衡方程求得；ω表示頻率；nk為該子系統的模態密度；這樣，隨機子系統與確定性子系統之間的能量關系便建立起來。

最后，得到確定性子系統位移q的互譜表達式：

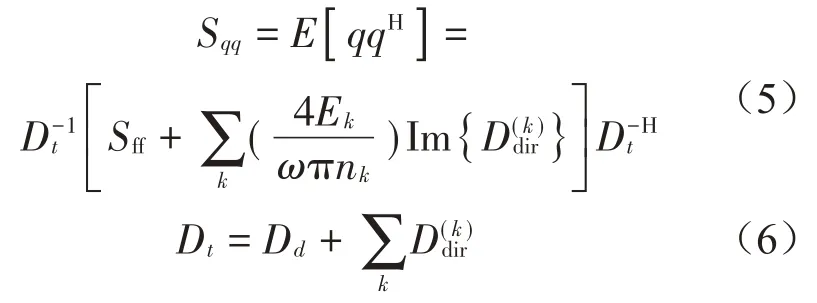
式中：Dt表示整體剛度矩陣；上標“-1”表示求逆運算；Sff表示外部激勵力的互譜。式（5）是確定性子系統位移響應互譜方程，是FE-SEA 法中確定性子系統動態響應求解方程。

3 基于FE-SEA法的噪聲預測與分析

3.1 激勵源的確定

由于平臺支持船上層建筑通常位于船艏，因此側推工況下，艙室噪聲的主要聲源包括側推裝置、主輔柴油機和側推柴油機，主推進器由于距離遠，其影響可以忽略。

3.1.1 側推槳脈動壓力

本文選擇的計算工況為側推柴油機驅動艏側推槳滿負荷工作，另一臺側推不工作。側推槳為4 葉調距槳，直徑2.0 m，額定轉速346 r/min，船舶航速取0.5 kn。為了采用CFD方法計算側推槳對導管壁脈動壓力，在完成船體幾何模型建模后，進行網格劃分，將計算域劃分為隨螺旋槳共同旋轉的旋轉水域和船體所處的靜水域。合并旋轉水域及靜水域網格，艏側推網格截面及靜水域邊界網格如圖1所示。

設置旋轉水域與側推螺旋槳繞槳的中心軸線同步旋轉，設置入流面為速度入口，出流面為Outflow，靜水域其余邊界面設置為對稱邊界。為保證收斂速度，先進行定常計算，待穩定后進行非定常計算。計算采用RNG k-ε模型，壓力及速度求解選擇SIMPLE方式，離散方式采用標準形式（Standard），離散格式為1階迎風形式。

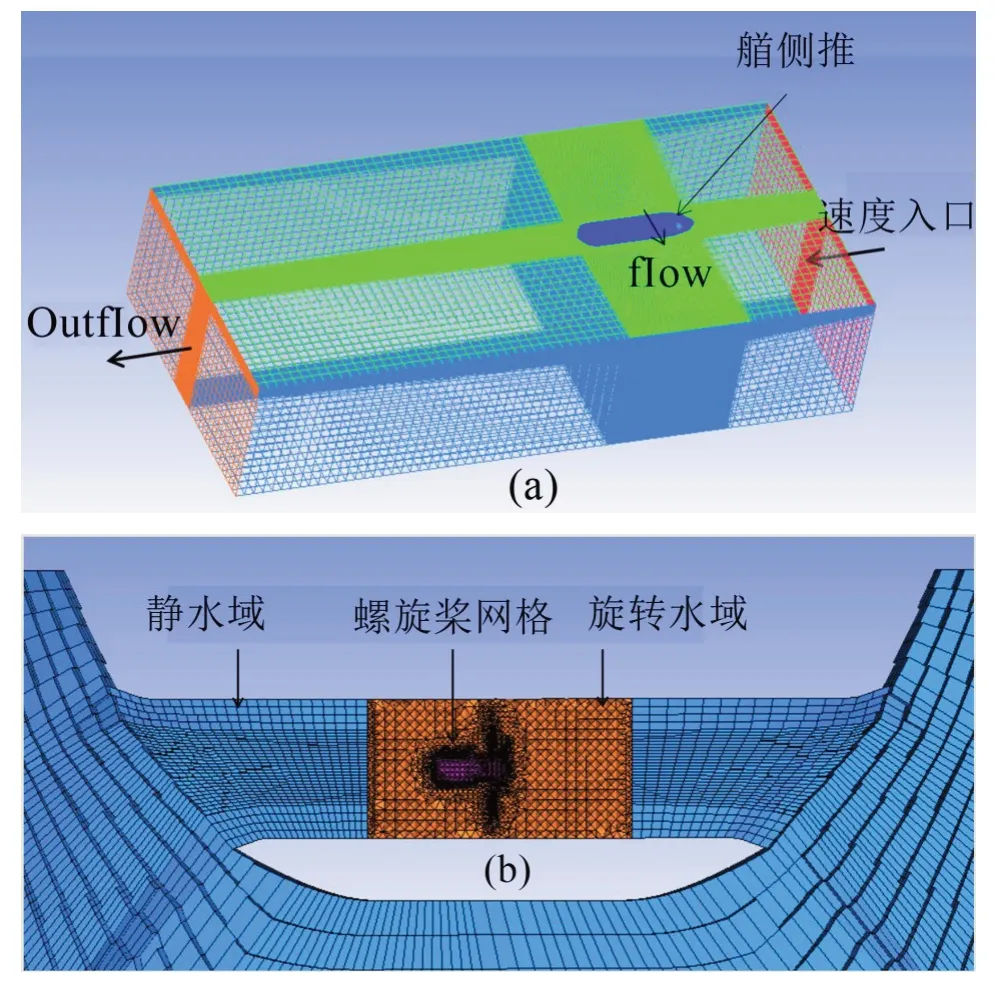
圖1 CFD網格與邊界條件

穩態收斂后得到側推螺旋槳葉面及葉背壓力，從而得到螺旋槳槳面壓力為134.07 kN，對比螺旋槳額定推力135 kN，結果符合實際情況。亦對比了旋轉水域與靜水域的交界面，發現交界面之間流場情況較為一致，交界面區域的數據交換符合要求。瞬態計算得到的導管壁面脈動壓力即為噪聲計算的側推槳激勵力，如圖2所示。

圖2 導管壁面壓力分布

為得到各節點在噪聲計算頻率上的激勵值，通過傅里葉變換可作出壓強-倍頻程折線圖，以導管中心段三個測點a，b，c為例，如圖3所示。分析導管表面力在噪聲計算頻率段的變化趨勢可以發現，導管中部（側推槳所在較窄區域）壓強高，但隨頻率的升高逐漸降低；導管入流區，低頻率段壓強高，隨后衰減迅速；其他大部分區域壓強低，且隨頻率的升高而小幅度降低。

側推工況下船體振動噪聲和導管內流場聯系緊密，由于流體的壓力不同，區域的規律也將不同，為準確反映整個導管內的壓力分布，導管可以依據CFD的計算結果以及精度需求被劃分為多個分段。

本文依據瞬態計算的實際結果，選取壓力近似的區域，如葉梢區、入流喇叭口較寬一側、入流喇叭口較窄一側等，按照壓力逐漸改變的規律詳細地分割導管為11部分。

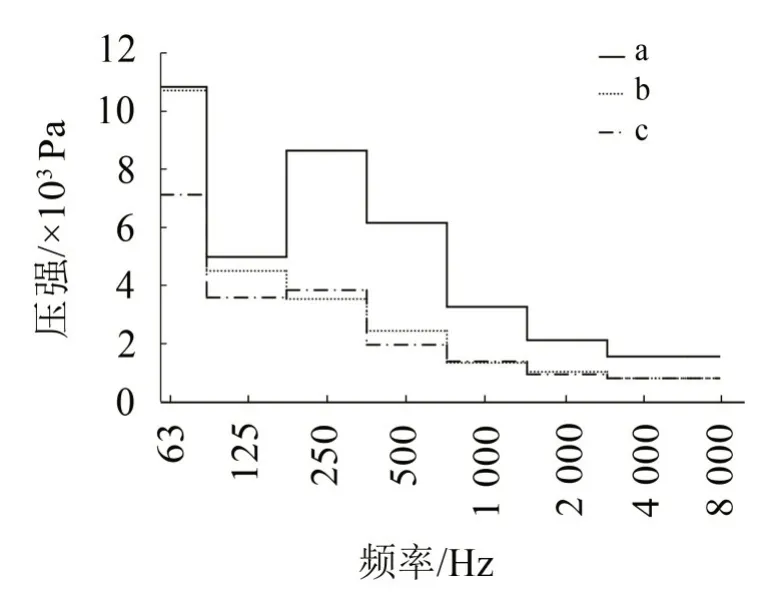
圖3 導管中心段樣本點的壓強-倍頻程折線圖

3.1.2 柴油機激勵

柴油機激勵源包括主輔機和側推柴油機的結構聲、機體輻射聲和排氣輻射聲。由于主輔機排氣管均裝有標稱35 dB(A)的消聲器，因此計算中未包括排氣噪聲。側推柴油機與輔機均以額定轉速運轉。

柴油機結構聲與空氣噪聲激勵按照下述經驗公式估算[12-13]：

（1）對于目標船舶的中高速柴油機結構噪聲，激勵源為柴油機機腳加速度級。

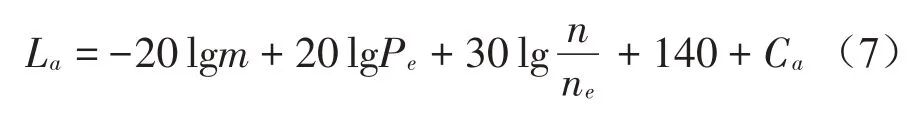
式中：La為機腳加速度級，m為柴油機質量，Pe為柴油機額定功率，ne為柴油機額定轉速，n為柴油機工作轉速，Ca為倍頻程修正值。

（2）對于柴油機空氣噪聲，激勵源為機艙區域的輻射聲功率級。

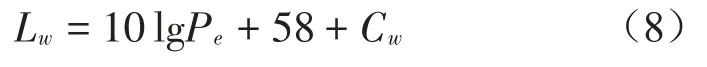
式中：Lw為輻射聲功率級，Pe為柴油機額定功率，Cw為倍頻程修正值。

3.2 FE-SEA模型建立方法

船體結構復雜，各組件模態數在全頻域變化較大，采用低頻到高頻逐漸由FE子系統過渡到SEA子系統的方式大大增加了建模復雜性，因此選擇特定分界頻率劃分不同子系統來簡化建模過程[10]。

上層建筑聲腔子系統以及其周圍主要的平板子系統的模態數在63 Hz以上均能滿足大于5的要求，符合SEA 方法的使用條件。導管分段的模態數如圖4所示。

在315 Hz 以下的模態數大部分小于5。因此，在頻率小于315 Hz 時，分段導管由于模態密度稀疏、剛度大，應采用確定性子系統建模。全船其他主要構件由于面積較大、剛度小且模態密集，應采用統計能量法建模。在軟件中建立導管FE Subsystems以及相應FE Faces，耦合到船體統計能量模型中。導管表面壓力以擴散聲場形式作用于各區域網格單元對應的FE Faces，導管FEA 模型如圖5所示。由于在63 Hz～315 Hz頻段中，各結構模態數呈現出低頻或是高頻特性，可根據混合法理論將63 Hz～315 Hz頻率范圍視為中間混合頻段簡稱“中頻”。

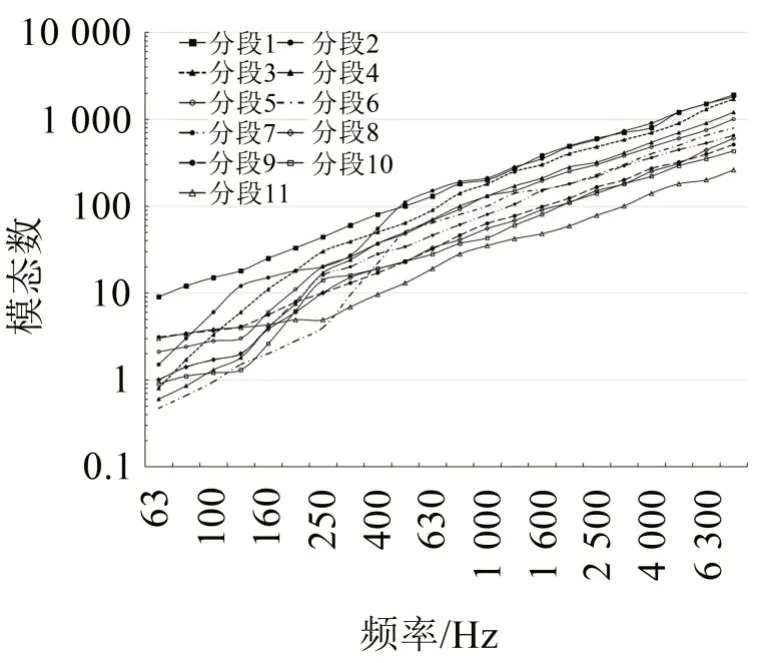
圖4 不同頻帶內導管分段模態數

圖5 導管FE子系統

在315 Hz～8 000 Hz 的高頻段，使用全船SEA模型進行分析。根據艙室分布和船體結構將船體的噪聲計算模型劃分為平板(包括平板和加筋板)、聲腔和半無限流體三類子系統。船用鋼的彈性模量為2.1×1011Pa，密度為7 850 kg/m2，泊松比為0.3。對于聲腔，多數采用一個封閉艙室對應一個聲腔子系統的形式。機艙以后的尾部區域的子系統劃分對上層建筑艙室噪聲的影響較小，為滿足SEA 計算要求，有些體積較小的封閉空間可以與鄰近子系統進行合并。但由于機艙包含多個噪聲源，將機艙的聲腔分割為包含主機、輔機及側推柴油機在內的多個聲腔子系統。計算所得的柴油機輻射聲功率級在軟件中以輸入功率（Power sources）的形式添加于機艙區域對應的聲腔子系統中，機腳處加速度級以約束（Constraints）的形式施加于柴油機所在船底板處。半無限流體用以模擬舷外水對船外板的作用。建立所有相鄰子系統間的連接，確保子系統間完全耦合，能量傳遞正常。最后，全船SEA模型如圖6所示。

3.3 計算結果分析

3.3.1 全頻段聲壓級

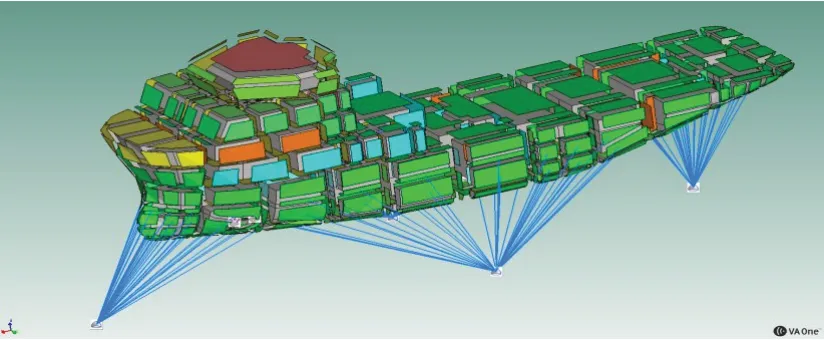
圖6 全船高頻段SEA模型

分別計算中、高頻段艙室噪聲值，可以得到艙室全頻段（63 Hz～8 000 Hz）聲壓級，圖7是部分艙室噪聲頻譜曲線。分析結果可以發現，隨著頻率增加，聲壓級呈減小趨勢。在全頻域存在著部分極大值點，在進行降噪處理時需要重點考慮。為了清晰看出各層甲板艙室聲壓級變化趨勢，選取160 Hz 及630 Hz兩個中心頻率得到聲壓級云圖，如圖8所示。

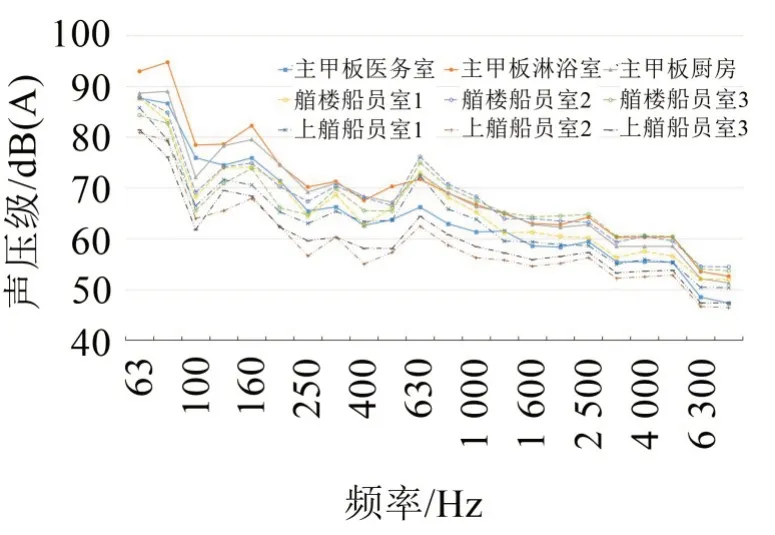
圖7 艙室全頻段聲壓級/dB

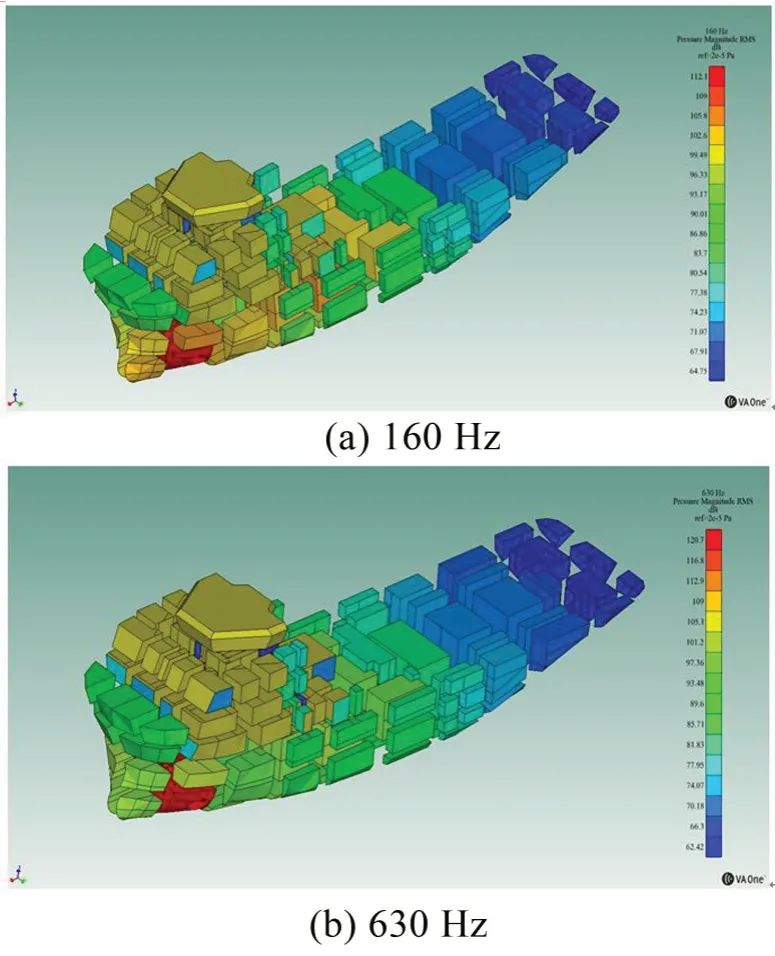
圖8 船舶艙室聲壓級云圖

3.3.2 FE-SEA 與SEA 兩模型在中頻段計算結果對比

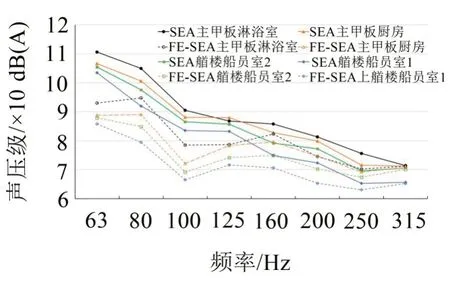
圖9 FE-SEA與SEA模型中頻段聲壓級/dB

為了研究本文算例采用FE-SEA 模型的必要性，船體包括導管又全部采用SEA 模型，進行中頻域SEA 模型的噪聲計算。比較兩種模型部分艙室在63 Hz～315 Hz頻段的聲壓級頻譜曲線，如圖9所示。可以看出，在該頻率范圍內，SEA 模型與FESEA 模型的頻譜曲線整體趨勢相同，但前者計算出來的噪聲水平普遍高于后者，而且結果差異較大，說明FE-SEA算法可以彌補SEA算法在中頻范圍計算精度的不足。而且隨著頻率的升高，兩模型之間結果差異逐漸縮小，說明隨著模態數的增加，SEA算法的計算精度逐漸提升。

3.3.3 總聲壓級計算值與實測值對比

對不同頻率下的聲壓級進行加權修正，采用A計權評價。為驗證數值計算結果的可信性，采用Larson Davis Model 831類精密積分聲級計進行了船舶不同工況下的噪聲測試。表1僅列出了計算工況下22個艙室噪聲A計權總聲壓級計算值與測量值。

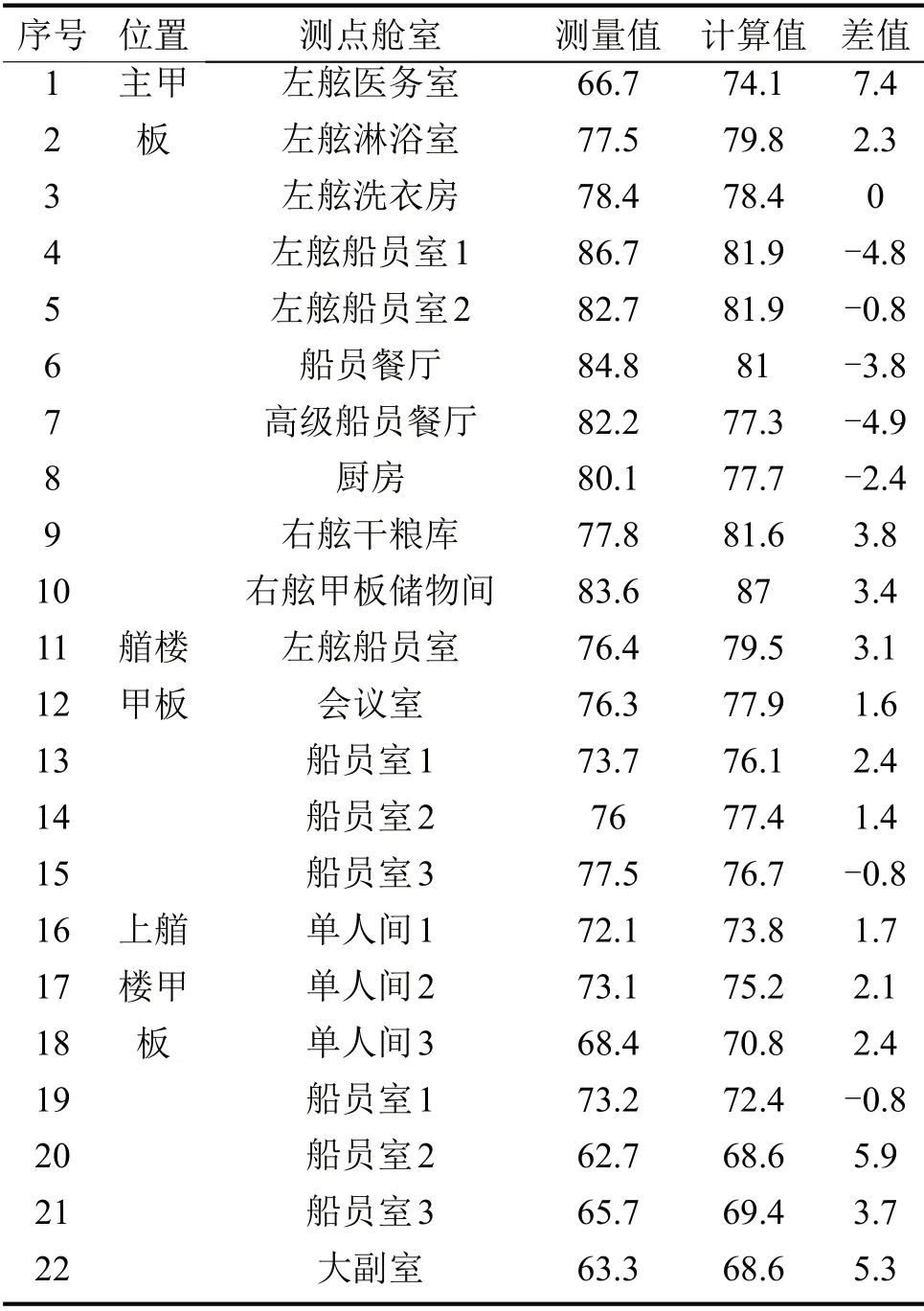
表1 計算值與實測值誤差表/dB（A）

表中1 號測點為主甲板醫務室，在噪聲的數值計算中，由于未對微穿孔吸聲材料進行考慮，因此醫務室的噪聲計算值與測量值誤差較大。除醫務室外的其余測點，計算值與測量值之間差值的絕對值平均為2.7 dB(A)，且分布規律一致。上層建筑艙室按照主甲板（測點2～10）、艏樓甲板（測點11～15）、上艏樓甲板（測點16～22）由低層至高層，艙室整體聲壓級水平呈下降趨勢。

3.3.4 不同激勵對噪聲的影響分析

為對比不同激勵源對艙室聲壓級的影響，將激勵源分為側推艙結構激勵、機艙結構激勵及機艙聲輻射激勵，其中側推艙結構激勵是指作用于側推導管的表面力，機艙結構激勵指主機、輔機與側推柴油機對機艙底板的激勵，機艙聲輻射激勵包括主機、輔機與側推柴油機的空氣激勵。對不同激勵作用下的船舶艙室噪聲分別進行計算，結果如圖10所示。

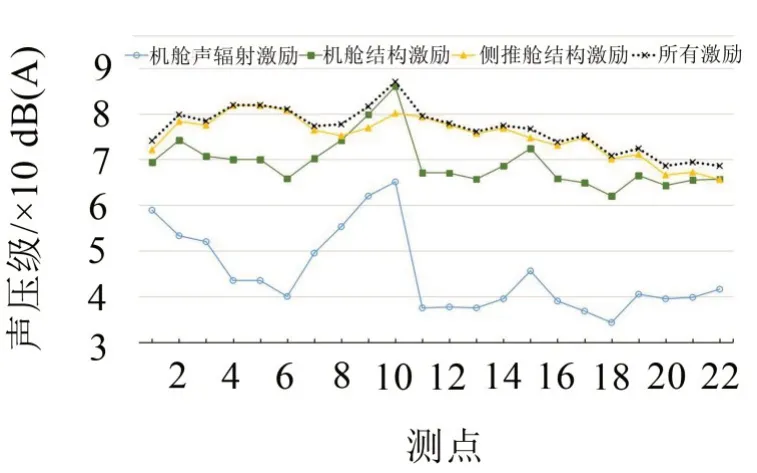
圖10 不同激勵作用下各艙室聲壓級

除個別艙室如9號與10號位于機艙的垂直方向主甲板上，噪聲受機艙結構聲源影響較大以外，大多數艙室噪聲受側推結構激勵的影響最大，機艙聲輻射激勵在船舶常規裝修下對船舶上層建筑的噪聲影響較小。聲輻射激勵與結構激勵下的艙室聲壓級曲線變化趨勢基本一致，且在遠離聲源的位置衰減得更為迅速。因此認為，船舶各層甲板艙室的總聲壓級水平與聲源相對位置有關，激勵源產生的能量在傳遞至遠距離艙室時會因為損耗而下降，其中輻射聲在傳遞過程中衰減最為明顯。

作不同激勵作用下的艙室聲壓級隨頻率變化的曲線圖，以主甲板餐廳為例，如圖11所示。

圖11 主甲板餐廳聲壓級

對比不同激勵源的作用效果，艙室聲壓級在1 000 Hz 頻率以后呈現下降趨勢，其中側推結構激勵曲線具有更大的下降幅度。但是側推結構激勵在低頻段上對艙室噪聲影響很大，因此能對大部分艙室聲壓級起主導作用。在1 000 Hz 以后的頻率上，機艙結構激勵引起的艙室噪聲值較大。

4 結語

本文針對平臺支持船普遍存在的側推工況下艙室噪聲狀況嚴峻問題，以某65 m AHTS 船為對象開展了艙室噪聲預測研究，得到了以下結論：

（1）在對平臺支持船這類船舶進行艙室噪聲預報時，為準確反映側推導管表面力對全船噪聲的影響，可以將導管有限元模型耦合到船體統計能量模型中，利用FE-SEA 混合方法進行求解。將中頻段FE-SEA 法及高頻段SEA 法整合得到的全頻域聲壓級與實測值對比，結果較為吻合。

（2）對比SEA 法與FE-SEA 混合法計算的噪聲值發現，由于中頻段不滿足SEA 法對模態數的要求，會造成較大誤差。單純采用SEA 模型所得聲壓級頻譜曲線普遍高于基于FE-SEA 混合模型計算的結果，這也驗證了中頻段使用FE-SEA 方法的必要性。

（3）對數值計算結果進行分析發現，側推工況下，大部分上層建筑艙室噪聲受側推激勵影響最大，個別靠近機艙的艙室，其噪聲受機艙內結構激勵影響大，聲輻射激勵對上層建筑艙室噪聲影響較小。