基于參數優化SVM的往復壓縮機氣閥故障診斷

韓亞洲，張 波，段禮祥，于興軍，范向增

(1.寶雞石油機械有限責任公司，陜西 寶雞 721000；2.中國石油大學(北京)機械與儲運工程學院，北京 102249)

1 引言

往復壓縮機是石油石化領域廣泛使用的關鍵設備，在油田現場，占A類設備總數的30%以上。由于往復壓縮機結構復雜，運動零件多，激勵源多，故障率較高[1]。其中氣閥是發生故障最頻繁的部件，閥片斷裂、彈簧失效和閥片磨損是常見故障，占氣閥故障的75%左右。氣閥故障[2]會引發連鎖反應，導致氣缸活塞系統進一步損壞，因此，對往復壓縮機氣閥進行狀態監測與故障診斷具有十分重要的意義[3]。

目前人工神經網絡[4-6]等智能算法在機電設備故障診斷中得到了大量的應用。但對于壓縮機這種大型設備來說，獲得大量的故障樣本數據比較困難。因此，應用人工神經網絡算法具有一定的局限性，而SVM[7-10]能夠在現有的信息下尋找到最優解，尤其在解決小樣本、非線性、局部極小等問題上具有獨特的優勢，因此更適合應用到壓縮機的故障診斷中。在SVM算法中，懲罰因子和核函數的選擇對診斷精度有很大的影響。目前參數優化的算法主要有網格搜索法[11]、粒子群算法[12]、遺傳算法等，其中粒子群算法和遺傳算法屬于啟發式算法，優點是尋優速度快，但在算法后期易陷入局部極小點；網格搜索法遍歷所有參數組合，在設定合適的搜索范圍和步距的前提下，可以快速搜索到最優參數組合。本文將網格搜索法運用到SVM參數尋優中，對油田現場大量的歷史數據樣本進行統計，對往復壓縮機氣閥常見故障進行分類識別，可以快速準確地診斷出壓縮機氣閥的故障。

2 方法原理

支持向量機(SVM)是一種以統計學習理論為基礎，以結構風險最小化為原則的數據挖掘技術，該技術是Vapnik在1995年提出的，在模式識別領域得到了廣泛應用。

支持向量機在數據分類時要求最優的超平面，對于樣本集(xi，yi)，x∈Rn，i=1，2，…，N，N是訓練樣本數目，n是樣本空間維數，y∈{-1，+1}是類別號，線性可分的超平面如圖1所示。

H為兩類樣本線性可分的超平面，H1和H2為過兩類樣本并且離超平面最近點的直線，它們之間的距離為分類距離。超平面的方程為

w·x+b=0

(1)

H1和H2的直線方程為

w·x1+b=+1

(2)

w·x2+b=-1

(3)

其中w是超平面的法向量，b是超平面的常項。

聯立式(2)和式(3)可以得出分類距離為

(4)

要使得分類間隔最大，等價于求下式的最小值

(5)

同時，還需要滿足以下方程，使得能夠將所有樣本進行正確分類

yi(w·xi+b)-1≥0i=1，2，…，n

(6)

式(5)和式(6)是最優分類超平面的2個基本條件，其中式(6)取等號的點為支持向量，直線H1和H2上的點就是支持向量。

根據相關理論，該問題就轉化為在式(6)的約束下求式(5)的最小值，目標函數Φ(w，b)是一個二次型函數，有唯一的最小值，可以構造拉格朗日函數進行求解，拉格朗日函數如下

αi≥0，i=1，2，…，n

(7)

其中αi是拉格朗日系數。

對上式中的w、b、αi分別求偏導并令其等于零，可得

(8)

(9)

(10)

經運算整理后可得最優化問題轉化為下列問題

(11)

(12)

αi≥0，i=1，2，…，n

(13)

(14)

(15)

其中x*(-1)和x*(1)分別表示兩類的任意某個支持向量。

對于線性不可分問題，一個超平面不能完全把樣本區分開來，于是引入了廣義超平面的概念，在超平面方程中加了松弛變量ξi，原方程變為

yi(w·xi+b)-1≥1-ξii=1，2，…，n

(16)

同時在目標函數Φ(w，b)中引入了懲罰項，其中c為懲罰因子

(17)

式中：c為常數，它控制對錯分樣本懲罰程度，若c過大，就會導致過學習，影響分類器的泛化能力，由此可見c是個重要參數。

與線性可分情況類似，也是構造拉格朗日函數求最優解，在此不詳述。

對于非線性問題，引入了核函數，從而原空間中線性不可分的樣本通過核函數的非線性映射，在高維空間中就可以實現線性分類。

核函數不同，就可以構造不同的分類決策函數，核函數通常有以下幾種核函數

(1)多項式核函數

K(x，y)=[(x·y)+1]d

(18)

(2)徑向基核函數

(19)

(3)Sigmoid核函數

K(x，y)=tanh[v(x·y)+α]

(20)

式(18)、(19)、(20)中：參數d、σ、α分別是核函數的重要參數，核函數的選擇會影響SVM的分類性能，影響SVM分類精度。

綜上所述，懲罰參數c和核函數參數d、σ、α是影響SVM分類器性能的關鍵參數，所以本文以(c，d)、(c，σ)、(c，α)作為尋優參數組合。

采用網格搜索法對參數組合進行尋優，該方法首先選定懲罰因子和核函數參數的取值范圍，設定搜索步距，形成一個二維網格，然后搜索網格，對參數組合進行優化，得到識別率最高的參數組合。

3 工程應用

3.1 參數優化

當選擇多項式核函數時，需要優化懲罰因子c和多項式階次d，其中c取值20、24、25和26，d取正整數1、2、3、4、5。圖2為不同c值下核函數參數d和識別率的關系曲線，當c=32，d=1和c=64，d=1時，識別率最高為88.57%，但是c偏大，容易存在過訓練問題，所以最優參數組合為c=32，d=1。

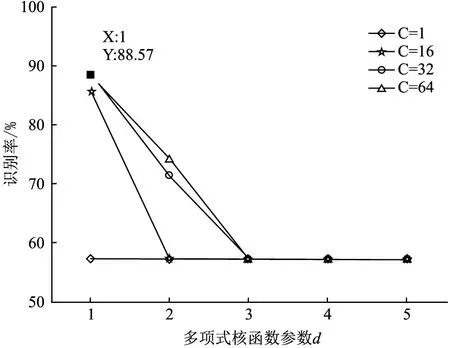
圖2 多項式核函數參數d和識別率的關系圖

當選擇徑向基核函數時，需要優化懲罰因子c和核參數寬度σ，其中c取值20、24、25和26，σ取值0.125、0.25、0.5、1、2、3、4、5。圖3為不同c值下參數σ和識別率的關系曲線，當c=1，σ取不同值時，識別率都比較低，隨著c的不斷增大，識別率增大后又減小。其中當c=32，σ=0.5和c=64，σ=0.5時，識別率為94.29%，但是懲罰因子c值越大，對錯分樣本的懲罰越大，會存在過訓練的問題。因此，最優參數組合為c=32，σ=0.5。

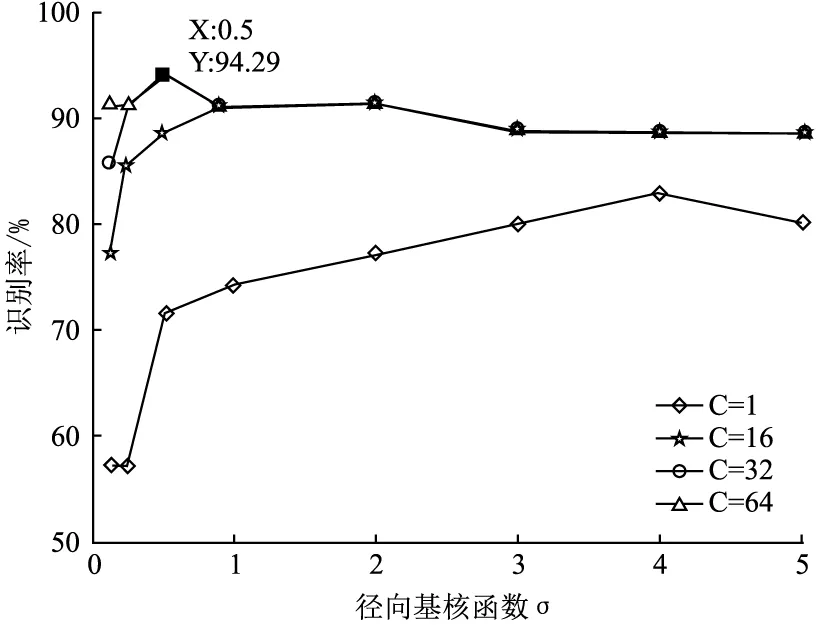
圖3 徑向基核函數參數σ和識別率的關系

通過以上的分析和驗證，選擇多項式、徑向基和Sigmoid核函數時，對氣閥狀態識別的識別率分別為88.57%、94.29%和91.43%，同時多項式核函數比較復雜，局部性差，Sigmoid核函數并不常用。綜合考慮，對氣閥故障識別時，選擇徑向基核函數(圖4)。

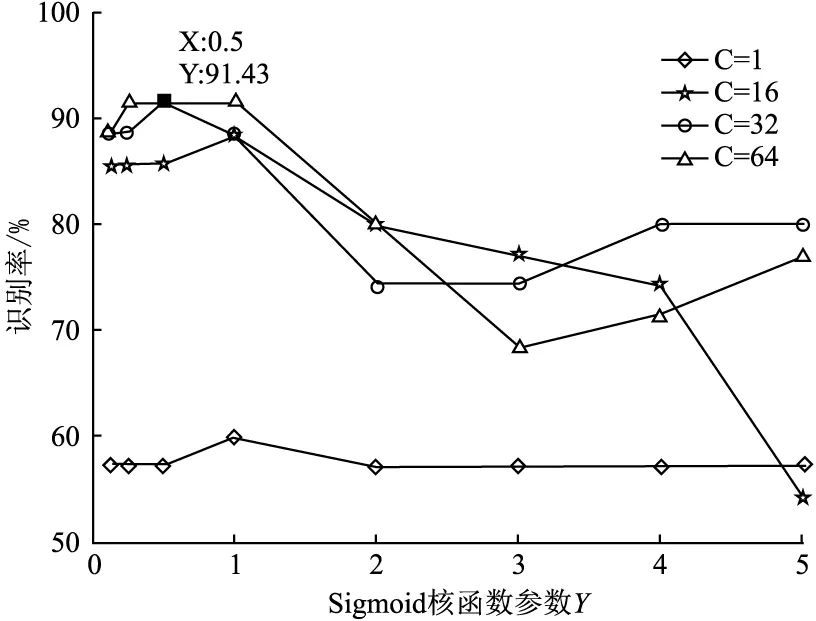
圖4 Sigmoid核函數參數γ和識別率的關系圖

3.2 實際應用

以西部某油田一聯合站的一臺壓縮機為例進行氣閥故障診斷研究，用某大學研制的MDES-5機械設備故障診斷儀采集氣閥閥蓋處的振動信號。

對氣閥振動信號進行經驗模態分解，將歸一化的固有模態分量作為特征參數，輸入SVM訓練。選取該壓縮機2005年到2010年采集的數據作為訓練樣本，其中氣閥正常訓練樣本30個，閥片斷裂、彈簧失效和閥片磨損時訓練樣本各8個，部分訓練樣本如表1所示。

通過表1中已知樣本特征向量的對比可以得出：閥片斷裂后，高頻分量增大，低頻分量減小，即E1/E增大，E8/E減小；彈簧失效后低頻分量增大，高頻分量減小，即E8/E增大，E1/E減小；閥片磨損后，高低頻分量同時有所增大，即E1/E和E8/E同時增大。因此可以考慮選擇E1/E和E8/E為2個主要特征，識別氣閥的4種運行狀態。用svmplot函數繪制識別結果可視化圖形，然后分別對氣閥正常和閥片斷裂、氣閥正常和彈簧失效、氣閥正常和閥片磨損等三組問題進行分類識別。

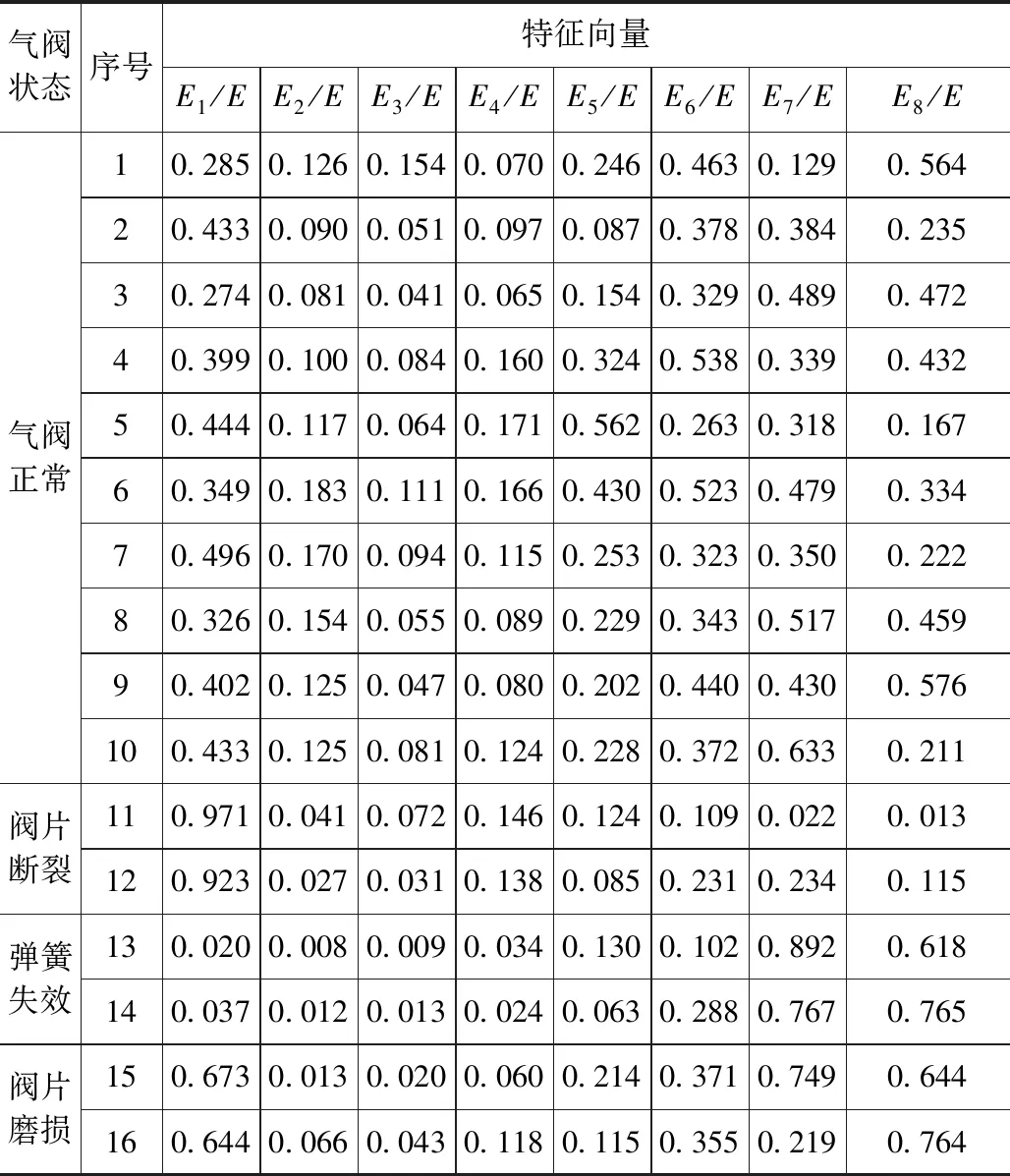
表1 氣閥各狀態下的部分訓練樣本

圖5～7分別為氣閥正常和閥片斷裂、氣閥正常和彈簧失效、氣閥正常和閥片磨損的識別結果，其中閥片斷裂樣本分布在右下角，彈簧失效樣本分布在左上角，閥片磨損樣本分布在右上角，四類樣本得到了很好的分離。

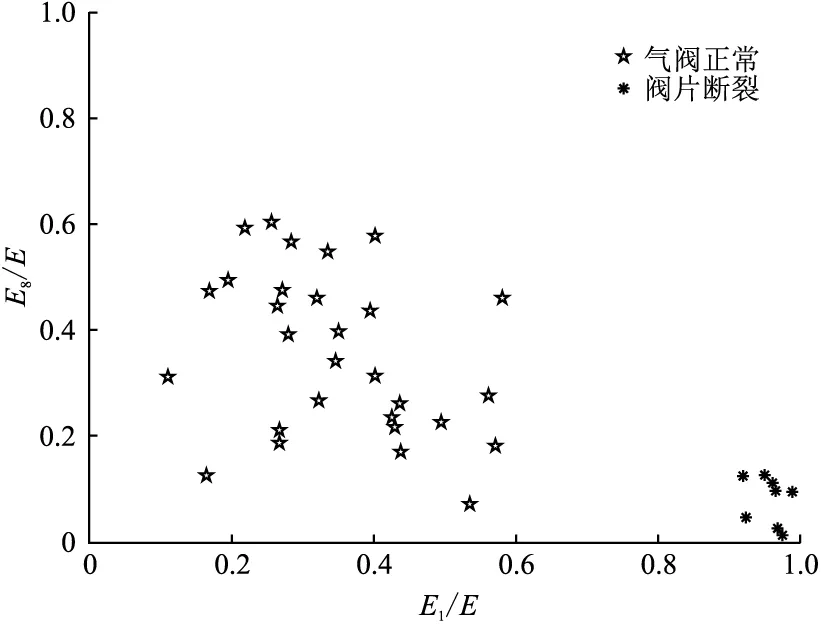
圖5 氣閥正常和閥片斷裂識別圖(訓練樣本)

為了驗證該方法識別的有效性，對2011年到2012年采集的16個未知樣本進行預測，預測樣本如表2所示。

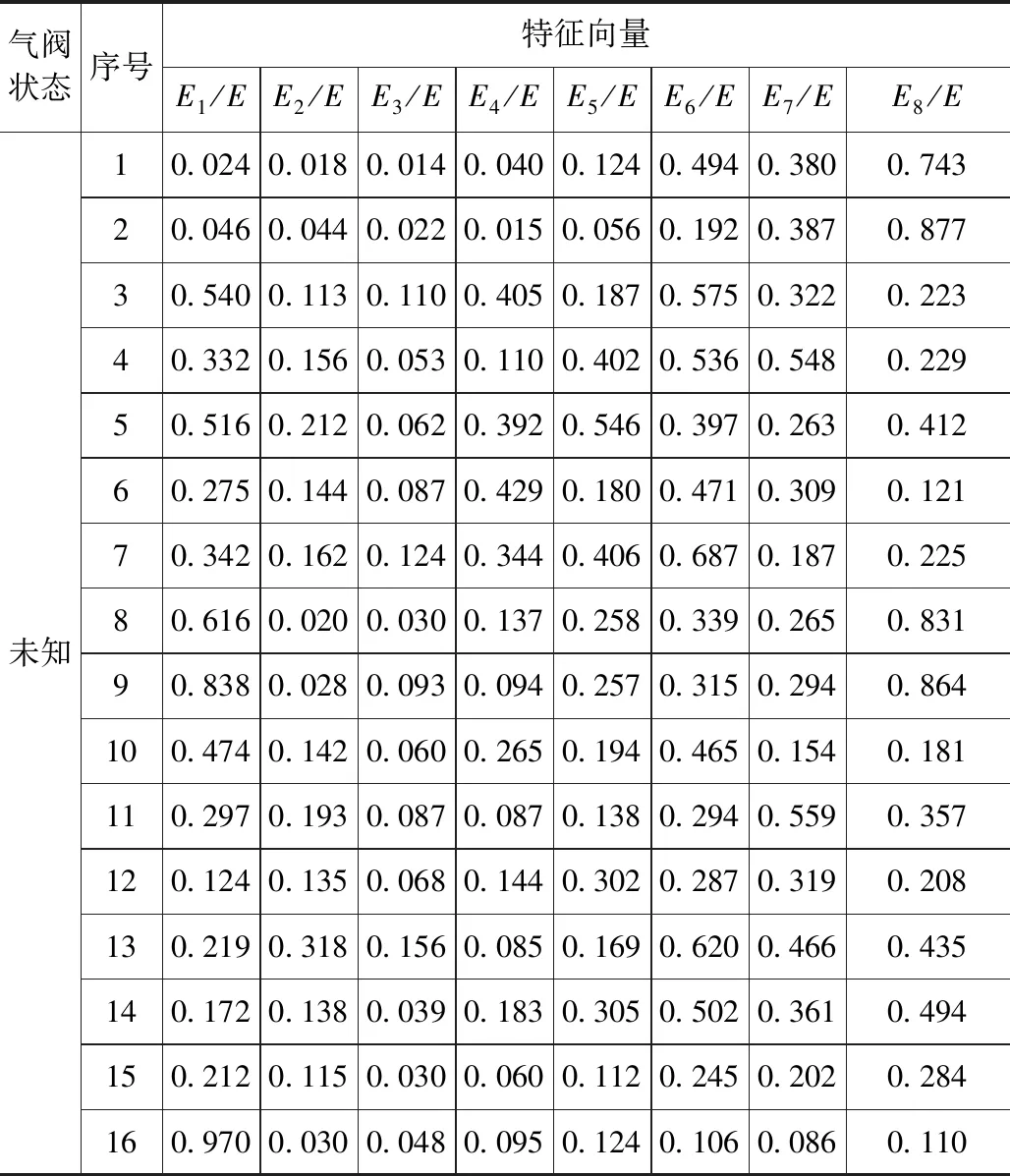
表2 氣閥未知狀態下的預測樣本

從預測結果可以看出，支持向量機將16個未知樣本劃分為四類，和已知訓練樣本的識別結果圖對比得出，11個為正常樣本，2個為彈簧失效，2個為閥片磨損，1個為閥片斷裂，該診斷結果和現場對比發現，有1個樣本診斷錯誤，誤將氣閥存在大量積碳診斷為正常，原因是氣閥訓練樣本還不全面。但從現場應用來講，該方法基本可以識別氣閥的4種基本狀態，則訓練樣本識別圖可以作為標準圖譜，為后續的診斷提供指導。

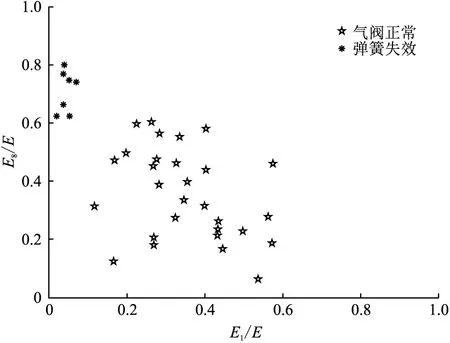
圖6 氣閥正常和彈簧失效識別圖(訓練樣本)

4 結論

氣閥故障的診斷和識別對于現場往復壓縮機的視情維修具有十分重要的意義。本文將固有模態分量的能量特征作為支持向量機的輸入，對已知的統計樣本進行訓練，建立分類模型，繪制可視化識別圖形，作為后續診斷的標準和參照。在此基礎上對未知樣本進行預測，識別結果和現場驗證基本保持一致。表明優化的支持向量機方法可以有效識別往復壓縮機氣閥的常見故障，可以在油田現場推廣應用(圖8)。

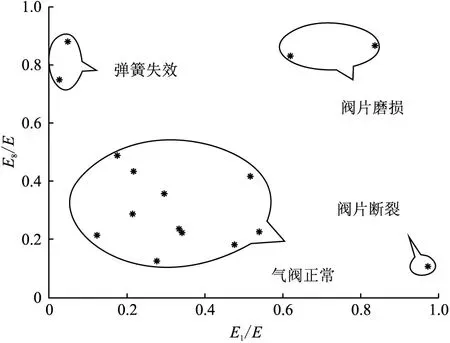
圖8 氣閥未知狀態識別圖(預測樣本)