一種輪式移動機(jī)器人滑模軌跡跟蹤控制器設(shè)計及其參數(shù)優(yōu)化方法

高興泉，丁三毛，黃東冬，劉志成，肖新宇

(吉林化工學(xué)院 信息與控制工程學(xué)院，吉林 吉林 132022)

目前，為了讓輪式移動機(jī)器人完成對復(fù)雜軌跡的跟蹤，常運用PID、自適應(yīng)、反演等算法設(shè)計軌跡跟蹤控制器[1].在種類繁多的控制方法中，建構(gòu)簡單、魯棒性強(qiáng)的滑模變結(jié)構(gòu)算法被廣泛用于輪式移動機(jī)器人軌跡跟蹤控制[2].一個控制性能優(yōu)良的滑模控制器，可以使輪式移動機(jī)器人更加穩(wěn)定、快速、精確地完成跟蹤控制.在設(shè)計滑模控制器時，趨近律的選擇

尤為重要，會直接影響控制器的性能，依據(jù)被控對象的特點設(shè)置適合的控制器，能夠使控制效果更好[1-3].其中指數(shù)趨近律在眾多趨近律中具有結(jié)構(gòu)簡單、趨近速度快的優(yōu)點，能夠在最短時間內(nèi)實現(xiàn)收斂.本文一共設(shè)計3個指數(shù)趨近律，其中外環(huán)由兩個指數(shù)趨近律設(shè)計，實現(xiàn)輪式機(jī)器人位置在x軸與y軸兩個分量的跟蹤控制，內(nèi)環(huán)由一個指數(shù)趨近律設(shè)計，實現(xiàn)輪式移動機(jī)器人在運動時對位姿角的跟蹤[3-4]，然后將所設(shè)計的控制器分別進(jìn)行Lyapunov穩(wěn)定證明確保每個控制器都能漸近穩(wěn)定.

在對滑模控制器設(shè)計時，參數(shù)的整定也是設(shè)計的難點.一組好的參數(shù)能夠大大提高跟蹤的速度，也能夠削弱抖振現(xiàn)象.起初一般是人工根據(jù)經(jīng)驗對參數(shù)進(jìn)行試湊整定，導(dǎo)致在選擇上出現(xiàn)較大的隨機(jī)性，較難選出較精確的參數(shù)，跟蹤品質(zhì)較差[5].隨著控制品質(zhì)的不斷增加，簡單的人工隨機(jī)調(diào)參已經(jīng)無法滿足高品質(zhì)的控制需求，而計算機(jī)技術(shù)的發(fā)展給復(fù)雜的調(diào)參帶來了曙光.科研人員很好的利用計算機(jī)的高速計算能力，經(jīng)過多次迭代，進(jìn)而尋找到一組最優(yōu)的參數(shù)，使控制效果更好.在眾多優(yōu)化算法中，蟻群算法、遺傳算法和粒子群算法等群智能算法可以解決滑模控制器參數(shù)選擇這一復(fù)雜問題[6].與其他算法相比，粒子群可以尋找最優(yōu)解、算法設(shè)計簡單易懂等優(yōu)點，在工程實驗中應(yīng)用比較廣泛.本文在設(shè)計在完滑模控制器后，為達(dá)到更好的控制效果，利用粒子群優(yōu)化算法強(qiáng)大的尋優(yōu)功能搜尋出一組最優(yōu)參數(shù)，更好更快地實現(xiàn)輪式移動機(jī)器人軌跡跟蹤控制，粒子群算法的加入大大降低了人工調(diào)參的隨機(jī)性和耗時性[5].

1 全動態(tài)誤差模型的建立及問題描述

根據(jù)圖1，本文所使用的輪式移動機(jī)器人模型有3個輪子，其中前面的輪子為導(dǎo)向輪，使輪式機(jī)器人轉(zhuǎn)彎更加靈活并保持輪式移動機(jī)器人的平衡，后面兩個輪子為驅(qū)動輪，為機(jī)器人的運動提高力矩及實現(xiàn)差速轉(zhuǎn)彎.

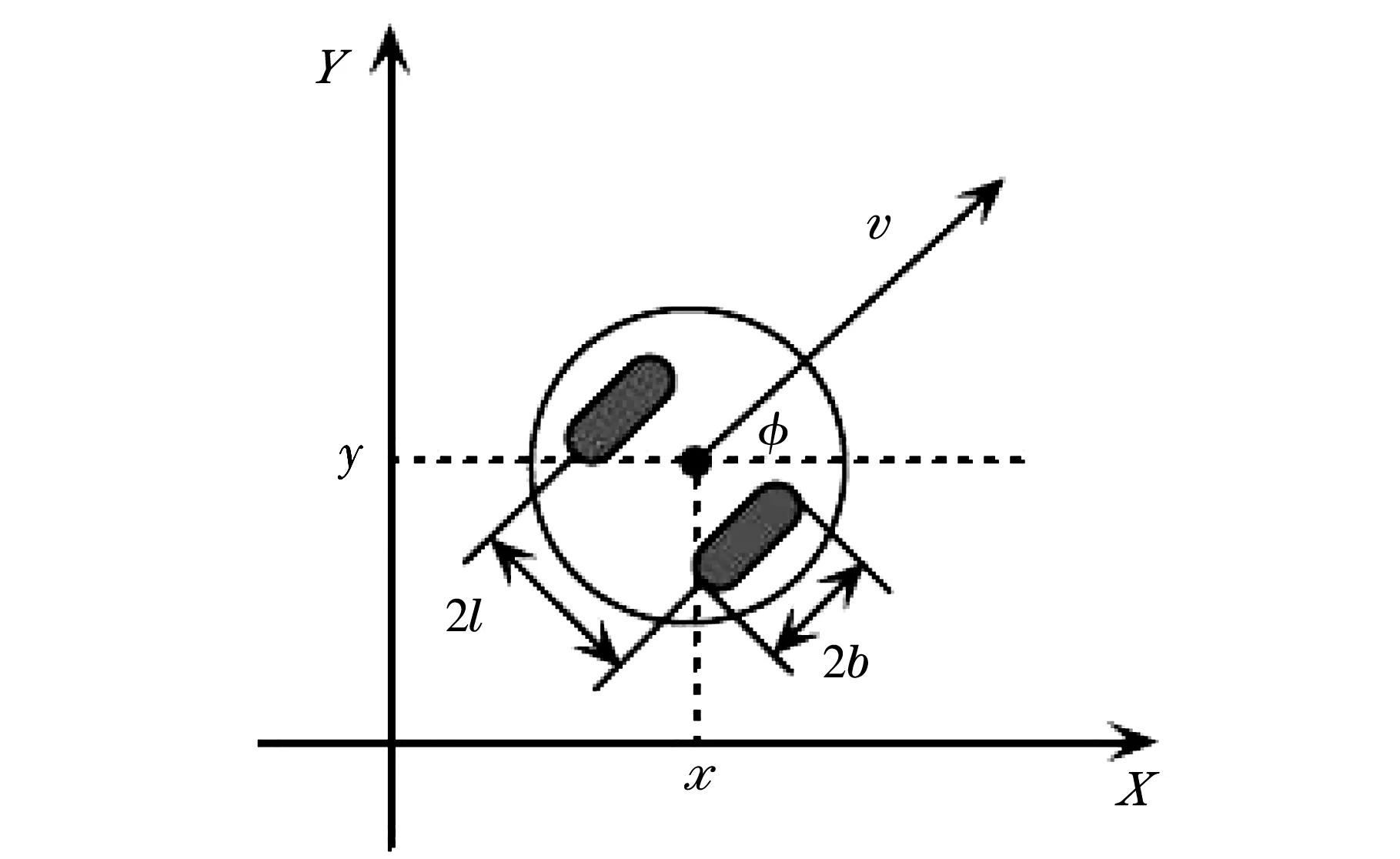
圖1 輪式移動機(jī)器人模型

假設(shè)輪式移動機(jī)器人運動過程中輪子只與地面發(fā)生滾動，可以對其運動的特點建立運動學(xué)模型為

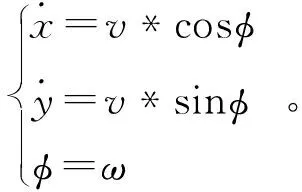
(1)

其中：x，y為運動時質(zhì)心的位置坐標(biāo)；φ為輪式移動機(jī)器人運動過程中軸線與x軸方向的夾角；v輪式移動機(jī)器人的瞬時速度[6].

2 滑模控制器的設(shè)計

2.1 閉環(huán)系統(tǒng)設(shè)計

整個閉環(huán)系統(tǒng)分為外環(huán)系統(tǒng)與內(nèi)環(huán)系統(tǒng)，其中位置子系統(tǒng)為外環(huán)系統(tǒng)，姿態(tài)系統(tǒng)為內(nèi)環(huán)系統(tǒng)，由內(nèi)環(huán)與外環(huán)共同構(gòu)成一個雙閉環(huán)系統(tǒng).圖2為閉環(huán)系統(tǒng)框圖.其中內(nèi)環(huán)輸入信號φd與 由外環(huán)與系統(tǒng)輸出提供.

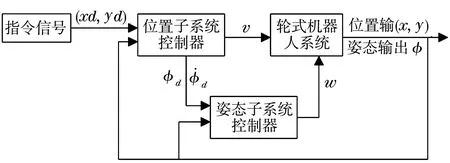
圖2 閉環(huán)系統(tǒng)結(jié)構(gòu)圖

2.2 位置控制律設(shè)計

首先對輪式移動機(jī)器人運動時的位置設(shè)計控制律，使輪式移動機(jī)器人在x，y坐標(biāo)軸方向上的運動軌跡趨近期望軌跡[6-7].

將期望軌跡定義為[xdyd]，則

(2)

其中xe=x-xd，ye=y-yd.

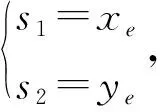
(3)

其中：k1,2>0，η1,2>0.

(4)

在輪式移動機(jī)器人運動時，如果φ跟蹤上φd運動的軌跡，則輪式移動機(jī)器人在姿態(tài)上完成跟蹤，而運動初始階段誤差的存在會影響系統(tǒng)穩(wěn)定.

為此，需要將式(4)求得的角度φ當(dāng)成理想值，即取

(5)

并設(shè)計一個比位置控制律收斂更快的姿態(tài)控制算法，使φ盡快跟蹤φd.

由u1，u2可知，可以得到輪式移動機(jī)器人速度v這個控制量

(6)

2.3 姿態(tài)控制律設(shè)計

為實現(xiàn)角度?能跟蹤上φd，對姿態(tài)控制律進(jìn)行設(shè)計，設(shè)計步驟參考位置控制律設(shè)計.設(shè)計姿態(tài)的指數(shù)趨近控制律為

(7)

其中，k3>0，η3>0.

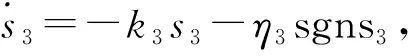
3 粒子群優(yōu)化輪式移動機(jī)器人滑模控制器

由于在滑模控制器設(shè)計時，趨近律系數(shù)與切換函數(shù)的邊界層厚度會嚴(yán)重影響輪式移動機(jī)器人軌跡跟蹤的效果，而這些參數(shù)在選擇時存在較大的隨機(jī)性，很難選出合適的參數(shù)實現(xiàn)高品質(zhì)的跟蹤控制.為了使輪式移動機(jī)器人更快更穩(wěn)地消除偏差，可以利用粒子群算法對趨近律系數(shù)與切換函數(shù)的邊界層厚度進(jìn)行優(yōu)化[8].

粒子群算法是一種通過大量參數(shù)進(jìn)行多次迭代，優(yōu)化出一個最優(yōu)結(jié)果的方法，可以對個體尋優(yōu)，也可也進(jìn)行全局尋優(yōu)[6].通過種群搜索最優(yōu)參數(shù)，在使目標(biāo)函數(shù)J的值最小的前提下實現(xiàn)輪式移動機(jī)器人軌跡跟蹤控制.粒子群算法流程如圖3所示.

圖3 粒子群算法流程圖

通過前面控制器的設(shè)計，該系統(tǒng)有6個參數(shù)可以優(yōu)化，分別是位置控制器設(shè)計時的k1，k2；姿態(tài)控制器設(shè)計時的k3，三個變量一一對應(yīng)的邊界層厚度η1，η2，η3等參數(shù)[9].圖4為粒子群算法優(yōu)化滑模參數(shù)系統(tǒng)框圖.

圖4 粒子群算法優(yōu)化滑模參數(shù)系統(tǒng)框圖

通過建立目標(biāo)函數(shù)J，以實現(xiàn)跟蹤時各個變量的偏差積分和最小為目標(biāo)，可建立各變量誤差與時間軸面積之和為目標(biāo)函數(shù)[9]，即：

(8)

在利用粒子群算法尋優(yōu)時，對6個參數(shù)設(shè)置的范圍均為0到50，隨機(jī)將這個范圍分成35個種群，每個種群進(jìn)化30次，從中選出一組參數(shù)使目標(biāo)函數(shù)J最小，改組參數(shù)即為這個范圍內(nèi)最優(yōu)參數(shù).由圖5為粒子群優(yōu)化時的適應(yīng)度曲線，由圖可知，適應(yīng)度值逐漸降低，在大約16代時達(dá)到穩(wěn)定狀態(tài).

圖5 適應(yīng)度曲線

通過粒子群算法的多次迭代，得到最后迭代的適應(yīng)度值大約為0.115，其中k1=42.787 9，k2=46.486 2，k3=48.985 8，η1=42.712 8，η2=39.512 0，η3=25.902 9.

4 實驗仿真及結(jié)果分析

實驗中對曲線軌跡進(jìn)行跟蹤，驗證設(shè)計的雙閉環(huán)滑模控制器能夠?qū)崿F(xiàn)軌跡跟蹤，同時進(jìn)行粒子群優(yōu)化得到的參數(shù)與人工經(jīng)驗整定參數(shù)進(jìn)行對比.通過人工經(jīng)驗進(jìn)行調(diào)整得到的參數(shù)為k1=0.3，k2=0.3，k3=3，η1=0.5，η2=0.5，η3=0.5.

以跟蹤曲線軌跡為例，該軌跡可以由以下函數(shù)描述

(9)

對輪式移動機(jī)器人的初始狀態(tài)進(jìn)行定義x0=-5，y0=5，φ0=5.輪式移動機(jī)器人在粒子群優(yōu)化參數(shù)與人工經(jīng)驗整定參數(shù)下的跟蹤軌跡如圖6所示.

x圖6 期望軌跡與輪式移動機(jī)器人運動軌跡

輪式移動機(jī)器人的初始狀態(tài)與目標(biāo)軌跡的初始狀態(tài)不同，導(dǎo)致輪式移動機(jī)器人在初始時刻各狀態(tài)均出現(xiàn)誤差，為了在各狀態(tài)體現(xiàn)出粒子群優(yōu)化得到的參數(shù)在控制效果上相對人工經(jīng)驗整定的更好，下面選取了位置、角度的誤差曲線進(jìn)行對比，如圖7所示.

時間/s圖7 曲線軌跡各變量誤差曲線

根據(jù)圖7所的對比結(jié)果，采用粒子群優(yōu)化得到的滑模控制器參數(shù)可以使輪式移動機(jī)器人的跟蹤誤差逐漸減少，即e→0，并保持穩(wěn)定的運行效果，相較于人工整定的參數(shù)具有更好的控制效果.同時，利用粒子群優(yōu)化算法進(jìn)行優(yōu)化，大大節(jié)約了人工進(jìn)行調(diào)參所花的時間，明顯提高了調(diào)整參數(shù)的效率[10].

5 結(jié) 論

為使輪式移動機(jī)器人實現(xiàn)軌跡跟蹤，首先從輪式移動機(jī)器人的運動學(xué)模型著手，根據(jù)輪式移動機(jī)器人的3個狀態(tài)，應(yīng)用滑模變結(jié)構(gòu)控制算法，分別在輪式移動機(jī)器人位置上的兩個狀態(tài)與姿態(tài)上的一個狀態(tài)設(shè)計控制器，可以使輪式移動機(jī)器人各狀態(tài)誤差收斂到0.在實現(xiàn)軌跡跟蹤后，應(yīng)用粒子群算法優(yōu)化所建立的目標(biāo)函數(shù)J，得到目標(biāo)函數(shù)最小時的最優(yōu)參數(shù).從仿真結(jié)果對比中明顯看出，通過利用粒子群優(yōu)化算法得到的參數(shù)在成功實現(xiàn)輪式移動機(jī)器人對曲線的跟蹤的基礎(chǔ)上，控制效果明顯比人工整定參數(shù)的控制效果更優(yōu)，大大提高了雙閉環(huán)滑模控制器的控制效果.這也體現(xiàn)出了將粒子群優(yōu)化算法應(yīng)用到所設(shè)計的滑模控制器后，大大提高滑模控制器控制效率.