考慮間隙影響的渦旋壓縮機轉子系統動態特性研究

（蘭州理工大學 石油化工學院，蘭州 730050）

0 引言

渦旋壓縮機相比于其他類型的壓縮機具有高效、低振和低噪等諸多優點而廣泛應用于動力工程、交通運輸以及空調制冷等領域。作為渦旋壓縮機的主要部件，轉子系統的工作狀態直接影響著渦旋壓縮機的穩定性。制造裝配誤差、材料變形及磨損等問題造成的運動副間隙，必然導致渦旋壓縮機的動不平衡。在渦旋壓縮機運行期間，含間隙運動副元素會發生接觸失真的現象，接觸時產生碰撞，引起非線性沖擊載荷，造成運動副的破壞以及影響壓縮機系統載荷的正常傳遞，降低了渦旋壓縮機的工作效率和可靠性。

國內外已有諸多針對渦旋壓縮機轉子系統的相關研究，李超等［1］針對變容量渦旋壓縮機曲軸系統，運用多體動力學和有限元方法，計算獲得了曲軸各軸承載荷及曲軸應力應變隨壓縮機轉速的變化規律，并對曲軸最大應力應變位置進行了安全性校核；邱海飛［2］通過建立的渦旋壓縮機主軸傳動系統等效力學模型，應用參數化建模與動態優化方法，獲得主軸系統自振頻率和振型，為改進主軸的動平衡性能，對主軸平衡重進行了優化設計；余洋等［3］考慮曲軸軸徑處存在運動副間隙條件下的動渦旋盤動力特性，分析了動渦旋盤的運動軌跡以及位移變化規律，為運動副間隙影響的渦旋壓縮機動平衡設計提供了參考；黃華軍等［4］針對小曲拐防自轉機構與動渦旋盤連接處存在運動副間隙的情況，分析了間隙數目與間隙大小對動渦旋盤及小曲拐接觸力的影響規律，總結了間隙位置的不同對渦旋壓縮機動平衡的影響。

上述研究分析了渦旋壓縮機轉子系統的振動、軸承受力以及運動副間隙對動渦旋盤和防自轉機構小曲拐運動特性的影響。但有關運動副間隙對曲軸動態特性的影響、渦旋壓縮機含間隙運動副對其瞬態動力性能的影響等方面的研究較少。本文以十字滑環為防自轉機構的渦旋壓縮機轉子系統為研究對象，在考慮運動副間隙的作用時采用非線性彈簧阻尼模型和庫侖摩擦力模型，基于多體動力學分析軟件，并結合有限元方法，詳細分析了運動副間隙下轉子系統的瞬態動力特性，可為渦旋壓縮機加工制造和裝配以及提高轉子系統動力特性提供理論依據。

1 渦旋壓縮機轉子系統模型

轉子系統的組成如圖1所示，曲軸由主、副軸承支承，曲柄銷處由滾針軸承將曲軸與動渦旋盤連接，在運行過程中，電機通過帶輪帶動曲軸驅動動渦旋盤作公轉平動，實現與靜渦旋盤的嚙合，完成對氣體的吸氣、壓縮及排氣過程［5］。

圖1 渦旋壓縮機轉子系統三維模型Fig.1 Three-dimensional model of rotor system for scroll compressor

2 運動副間隙力學建模

在渦旋壓縮機運行期間，運動副間隙的存在使得軸與軸承之間的理想接觸產生了松動，造成接觸失真現象，軸與軸承之間從接觸狀態到自由運動狀態，再到接觸狀態，整個過程包含著接觸與碰撞。旋轉副間隙中含有潤滑油，可將這種接觸考慮為彈簧阻尼模型，根據文獻［4］與文獻［9］建立接觸碰撞模型。

2.1 運動副間隙的矢量模型

如圖2所示，在平面旋轉鉸內引入一個間隙矢量來表達間隙矢量模型［6-8］。

圖2 間隙矢量模型示意Fig.2 Schematic diagram of joint clearance vector model

間隙矢量可以反映運動副間隙元素之間的相對位置，可有效處理間隙運動副連接點相對位置的變化，間隙大小用軸承半徑與曲柄銷半徑之差來描述，則：

式中 c——間隙；

rj——軸承半徑；

ri——曲柄銷軸半徑。

定義XOY為廣義坐標系，間隙矢量定義在一個局部浮動笛卡爾坐標系xjojyj中，以軸承的回轉中心為間隙矢量的基準起始點，矢量方向指向曲柄銷和軸承相對運動的接觸點，終點為曲柄銷的回轉中心。由圖可得，曲柄銷中心與驅動軸承中心的間隙矢量eij可表示為：

間隙矢量的大小可表示為：

式中 ex，ey——軸承中心到曲柄銷中心距離在X和Y方向的分量。

曲柄銷與驅動軸承之間的穿透深度δ為：

2.2 運動副間隙的接觸碰撞力模型

接觸碰撞模型將碰撞過程歸結為“自由運動-接觸變形”兩種狀態的隨機變換，通過考慮接觸表面的阻尼和彈性因素，比較真實地描述了碰撞過程。本文采用的是一種間隙非線性連續接觸碰撞力模型［9］，是基于 Lankarani-Nikravesh 接觸模型與彈性模型的融合。其表達式為：

式中 Fn——接觸碰撞力；

K——非線性剛度系數；

δ——接觸點的法向穿透距離；

n——冪指數，取決于碰撞材料的種類，一般金屬材料為1.5；

C——阻尼系數；

E*——接觸表面的彈性模量；

μi，μj——2 種材料的泊松比；

Ei，Ej——2種材料的楊氏模量；

Cr——恢復系數，代表能量耗散，其值小于1，為碰撞前后的速度之比。

2.3 運動副間隙的摩擦力模型

為了進一步真實地描述運動副間隙，必須考慮接觸時的切向摩擦力，采用修正的庫侖摩擦模型［9］，切向摩擦力在可以表示為：

式中 vt——接觸點相對滑移速度的切向分量。

此模型中的摩擦因數并不是一個常數，而是一個關于切向滑移速度的動態摩擦函數，表達式為：

式中 vs——靜摩擦臨界速度；

vd——最大動摩擦臨界速度；

μd——動摩擦系數；

μs——靜摩擦系數。

2.4 ADAMS接觸碰撞力函數

ADAMS軟件內置的接觸碰撞力函數是IMPACT函數，其采用非線性彈簧阻尼器來計算接觸碰撞力，IMPACT接觸碰撞力的計算公式為：

Cmax——最大阻尼系數；

dmax——在最大阻尼系數前提下的穿透邊界深度。

3 渦旋壓縮機轉子系統動力學分析

3.1 建立轉子系統動力學模型

根據表1，2所示的轉子系統參數，通過SOLIDWORKS建立渦旋壓縮機轉子系統三維模型，驅動軸承材料為GCr15，密度為7.83 g/mm3，彈性模量219 GPa，泊松比為0.3。其型號為IS4215，外徑62 mm，內徑50 mm，滾針個數為55，滾針直徑3.5 mm，長度為26.25 mm。然后導入ADAMS軟件中建立動力學模型，模型如圖3所示。

表1 型線及渦旋盤參數Tab.1 Profile and parameters of scroll member

表2 轉子系統各部件參數Tab.2 Parameters of each component of the rotor system

圖3 轉子系統動力學模型Fig.3 Dynamic model of rotor system

3.2 施加載荷及約束

根據運動副間隙對渦旋壓縮機動平衡的影響，所建立的模型中曲柄銷和驅動軸承連接處采用接觸副連接，同時設置庫侖摩擦力參數。根據轉子的真實運動情況在VIEW中對各個部件施加約束以及旋轉驅動并設置相應的轉速函數。

3.3 動力學仿真結果與分析

由于曲軸與驅動軸承之間存在間隙，兩者之間存在碰撞，引起轉子系統的非理想狀態運行，因此針對驅動軸承和曲軸進行測量。設置4個間隙梯度，分別為0（理想間隙），0.01，0.03，0.05 mm。

圖4（a）（b）分別示出了曲軸的質心軌跡及局部放大，由圖可知理想情況下曲軸的軌跡為一標準圓形，當存在間隙時質心軌跡出現了折點，而且間隙越大同一個軌跡中折點之間的距離會相應增加，曲軸的質心軌跡相對于理想情況的偏移越大。

圖4 曲軸位移Fig.4 Crankshaft displacement

圖5（a）（b）分別示出了驅動軸承分別在水平與垂直方向上的速度變化規律，理想情況時速度曲線為光滑的正余弦曲線，存在間隙時速度曲線沿著理想情況下的曲線上下波動，隨著間隙的增加速度曲線波動的峰值增大，但波動頻率減小。

圖6所示（a）（b）分別示出了驅動軸承在水平與垂直方向上的加速度變化，間隙為0時加速度曲線為正余弦曲線，間隙情況下的曲線沿著理想情況曲線上下劇烈的波動，并且曲線峰值隨著間隙的增加而增大。

圖5 驅動軸承速度Fig.5 Driving bearing velocity

圖6 驅動軸承加速度Fig.6 Driving bearing acceleration

圖7示出了運動副間隙處的接觸力隨時間的變化規律，理想情況下接觸力約為2 200 N，間隙條件下的接觸力出現了高頻率的波動，隨著間隙的增大，接觸力的瞬時峰值也逐漸增大，間隙值為0.05 mm時，曲軸與驅動軸承之間的接觸力最大可達8 000 N左右，隨著轉動周期的增加，接觸力逐漸減小并在4 000 N的范圍內上下波動。

圖7 曲柄銷與驅動軸承之間的接觸力Fig.7 Contact force between crank pin and driving bearing

從圖8可知，不含間隙時驅動軸承角速度約為303 rad/s，第一個轉動周期內，角速度呈現大幅度的波動，在間隙值為0.05 mm時，最大值約為304.4 rad/s，隨后波動峰值逐漸減小，并沿著303 rad/s上下波動。

圖8 驅動軸承角速度Fig.8 Driving bearing angular velocity

圖9示出了驅動軸承角加速度隨時間的變化，理想情況下驅動軸承角加速度為零，間隙的存在對角加速度的影響十分敏感，角加速度的變化十分劇烈且瞬時峰值較大。在間隙值為0.05 mm時，穩定后的角加速度在3500 rad/s2內波動。

圖9 驅動軸承角加速度Fig.9 Angular acceleration of driving bearing

間隙接觸力、位移、速度、加速度、角速度以及角加速度的值均會隨著間隙的增加而增大，但其波動的頻率均會隨著間隙的增加而減小。這是由于間隙增加時，驅動軸承與曲軸之間從接觸狀態到自由運動狀態的時間也相應地增加，接觸力變化的頻率也就越小，但接觸力的大小將變大，而力的增大導致了速度、加速度、角速度和角加速度等也隨之增大。速度增大將導致曲軸與驅動軸承再次接觸碰撞前構件動能增加，碰撞力增大；加速度越大，相同時間內構件速度的增速就越大，曲軸與驅動軸承再次碰撞時的碰撞力就越大；該過程是連續交替循環的，會形成惡性循環，使構件之間的磨損加劇，間隙再次增大，因此，需要對渦旋壓縮機進行動平衡以控制間隙處于合理的范圍，以防降低渦旋壓縮機的效率甚至失效。

4 渦旋壓縮機轉子系統瞬態特性分析

瞬態動力學分析是對隨時間任意變化的載荷作用下，結構動力響應過程的分析，動力學通用方程如下：

式中 ［M］——質量矩陣；

［C］——阻尼矩陣；

［K］——剛度矩陣；

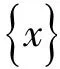
4.1 轉子系統有限元模型建立

將轉子系統三維模型導入到軟件中，進行材料屬性的定義，然后選擇合適的網格進行劃分，得到371 470個節點以及83 767個單元，如圖10所示。

圖10 轉子系統網格劃分Fig.10 Mesh division of the rotor system

4.2 施加載荷及約束

根據轉子系統的運動特點，選擇合理的載荷及約束是模擬的必要條件。首先，由于主、副軸承起支撐作用，本文采用軸承單元進行代替，如圖11所示。

圖11 軸承單元簡化Fig.11 Simplified diagram of bearing unit

曲柄銷處施加遠端約束，曲軸尾端帶輪處施加柱面約束，均限制軸向位移。然后在曲柄銷處設置角加速度約束，并將獲得的驅動軸承角加速度數據輸入，以此作為瞬態分析的邊界條件對曲軸進行分析；設置轉速范圍，輸入不同的間隙下的剛度系數，以此對曲軸進行臨界轉速計算分析。

4.3 有限元仿真結果與分析

通過WORKBENCH軟件計算分析可獲得不同間隙值下應力分布情況，如圖12所示。

在曲軸與動渦旋盤連接的曲拐處、曲軸與帶輪連接的軸肩位置均發生了應力集中現象，并且曲軸與動渦旋盤連接的曲拐處的應力最大，這是因為曲柄銷與主軸連接處軸徑突變和曲柄銷偏心導致曲柄銷旋轉離心力增加而引起應力集中。圖12（a）所示，間隙為0.01 mm時曲軸的等效應力為25.3 MPa；圖12（b）所示，間隙為0.03 mm時曲軸的等效應力為30.6 MPa；圖12（c）所示，間隙為0.05 mm時曲軸的等效應力為36.4 MPa。隨著間隙的增大，發生應力集中部位的應力也相應增大，這是因為不同間隙下曲軸與驅動軸承之間的接觸力載荷發生了變化，接觸力的大小隨間隙增大而增大，使應力集中現象更加嚴重，而且曲軸的受力過程是連續交替循環的，這會給曲軸的安全運行帶來更大的隱患。

圖12 不同間隙下曲軸應力分布云圖Fig.12 Crankshaft stress distribution nephogram with different clearances

間隙為 0.01，0.03，0.05 mm 時，曲柄銷與驅動軸承的接觸剛度分別為：2.90×107，2.08×107，1.35×107N/m。經過WORKBENCH軟件計算分析可畫出不同間隙下曲軸系統的坎貝爾圖，如圖13所示分別為0.01，0.03，0.05 mm間隙時曲軸的坎貝爾圖，圖中的三角形分別表示不同間隙下曲軸系統的臨界轉速，由圖可知同一間隙下該曲軸有2個臨界轉速，而不同間隙情況下的第一階臨界轉速均小于9.13 rad/s，對應的第二階臨界轉速分別為 1 447.4，1 444.3，1 438.6 rad/s。

圖13 不同間隙下曲軸坎貝爾圖Fig.13 Campbell diagram of crankshaft with different clearances

為了保證轉子正常運行，需要使轉子工作轉速避開臨界轉速，其安全裕度一般為10%～20%以上。結合圖可知，由于第1個臨界轉速很小，轉子可以很快跨躍，不會產生共振，對于第2個臨界轉速而言，間隙小于0.05 mm時，第2個臨界轉速為1 450 rad/s（約為13 800 r/min），遠大于渦旋壓縮機正常運行轉速范圍2 500～4 000 r/min，因此此種情形下也不會引起共振現象。然而當渦旋壓縮機向高轉速發展時，就必須考慮間隙對該臨界轉速的影響，否則轉速越大，間隙越大時，越接近該臨界轉速，轉子發生共振的可能性就越大，圖14所示為曲軸的臨界轉速隨間隙大小的變化情況。

圖14 不同間隙下曲軸臨界轉速Fig.14 Crankshaft critical speed with different clearances

由圖可知，當間隙小于0.05 mm時，隨著間隙的增大，曲軸系統的臨界轉速隨之緩慢降低，是因為間隙的存在破壞了曲柄銷與驅動軸承的接觸剛度并使其發生變化，接觸剛度隨間隙的增大而減小，從而使曲軸系統的臨界轉速隨之變小。當間隙大于0.05 mm時，曲軸臨界轉速隨著間隙增大降低越快，極大地增加了渦旋壓縮機發生共振的可能性，需要通過嚴格控制間隙大小和施加預緊力等措施以增加接觸剛度，以避免轉子共振現象。

5 結論

（1）同一間隙下，曲軸的位移波動最小，驅動軸承角速度的波動較大，角加速度的波動最大。

（2）不同間隙時，曲軸及驅動軸承的位移、角速度、角加速度以及間隙接觸力均呈現不同程度的波動，隨著間隙增大，波動幅值越大，但波動頻率降低。

（3）曲軸與驅動軸承以及帶輪連接處均發生了應力集中現象，而間隙的存在使曲軸的應力集中現象加劇，隨著間隙的增大，曲軸所受的應力也逐漸增大。

（4）間隙的存在改變了曲柄銷與驅動軸承的接觸剛度，間隙增大，剛度減小，導致曲軸系統的臨界轉速降低，增加了轉子共振的危險。