異構部分重復碼的構造①

孫 偉,沈克勤,張鑫楠,何亞錦

(長安大學 信息工程學院,西安 710064)

近些年,隨著信息技術和大數據產業的發展,數據量激增,傳統集中存儲設備已無法滿足海量數據存儲要求.分布式存儲系統(DSS)應運而生,DDS是由許多廉價磁盤組成,具有成本低、可用性強和可擴展性高等突出優勢.它作為可存儲大量數據的存儲系統已經被許多互聯網企業應用,例如Microsoft和Facebook[1,2].然而分布式存儲系統的節點易發生故障而造成數據丟失,所以故障節點的修復成為研究的重點.

主要通過復制和編碼來保證數據的可靠性.傳統的DSS 多采用復制(replication)策略[3],其中三副本最為常見.將文件復制2 次即得到3 個副本,分別將其存儲到系統的不同節點.當有節點發生故障導致數據丟失,可以通過其他正常節點的副本進行修復.但是其占有的存儲系統開銷過于龐大.于是Dimakis 提出了糾刪碼(erasure codes)策略[4].與復制策略相比,經典的糾刪碼具有更大的數據可靠性和較小的存儲開銷.其中最大距離可分(Maximum Distance Separable,MDS)碼獲得最優的存儲開銷性能.但是糾刪碼修復故障節點時需要的修復帶寬開銷過大.由于上述缺陷,Dimakis等[4]開創性的提出并介紹了再生碼,研究發現在故障節點修復時其的修復帶寬開銷明顯降低.但是再生碼修復故障節點時需要大量有限域的運算,計算復雜度大.

2010年Rouayheb 提出了部分重復(Fractional Repetition,FR)碼,FR 碼是一種精確最小帶寬再生碼,修復故障節點時的修復帶寬減小,同時不需要大量有限域的運算,計算復雜度較小[5,6].所以越來越多研究人員開始研究FR 碼,Ramamoorthy 設計的FR 碼引入了組合設計的思想[7].相繼利用二部圖[8],Steiner 系[9]和序列[10]構造FR 碼.隨后研究人員又研究了FR 碼的修復消耗最小化[11].

部分重復碼的現有編碼方式節點的存儲容量基本相同,同時重復度也基本相同,都屬于同構編碼方式,但是分布式存儲系統由于設備故障,硬件差別等原因,導致存儲成本不同,各個節點存儲容量不同,因此需要異構編碼方式.本文提出基于Hadamard 矩陣和[7,3,4]圖形分別構造異構的部分重復碼的一般算法.與現有的FR 碼相比,采用Hadamard 矩陣和[7,3,4]圖形構造FR 碼更加簡潔明了,其中基于Hadamard 矩陣可實現由同構經過簡單變換為異構編碼方式;基于[7,3,4]圖形構造FR 碼可實現擴展延伸,若當前結構無法滿足需求,可對其進行擴展,直至滿足需求,而且無需改變現有結構.經過與RS 碼理論分析對比發現,設計的兩種異構FR 碼的修復局部性、修復帶寬開銷進一步降低,且可以實現故障節點精確無編碼修復,修復復雜度較低,修復效率較高,減少了修復故障節點的時間.

1 基礎知識

1.1 Hadamard 矩陣

定義1[12].滿足:HnHnT=nIn>;Hn是一個n階方陣其由1 或?1 構成,In是一個n階單位矩陣,稱Hn為n階Hadamard 矩陣.

Hadamard 矩陣具有如下性質:

(1)將Hadamard 矩陣的任意兩行(列)交換,矩陣的任意一行(列)的所有元素乘?1,得到的矩陣仍然是Hadamard 矩陣.

(2)若Hn是n階Hadamard 矩陣,需要滿足n是4的倍數(n＞2).

本文所需的Hadamard 矩陣均為標準型,即Hn的第1 行和第1 列全是1.

1.2 部分重復碼

定義2[13].FR 碼.給定一個部分重復碼C=(?,M),其中參數為(n,k,d),將重復度設為ρ(即編碼數據塊復制ρ倍),特定地,M={M1,···,Mn}為n個子集的集合,Mi(1 ＜=i＜=n)中的每一個元素都屬于集合?={1,···,θ}.

另外還需滿足以下兩個條件:

1)每個子集的大小為d;

2)?中每一個元素分別存在于M的ρ個子集中.

如果d和ρ 分別都為固定值則為同構FR 碼,如果d不是固定的值則為存儲容量異構的FR 碼;如果 ρ不是固定的值則為重復度異構的FR 碼.

FR 碼的本質為將經過MDS 編碼后的數據塊復制ρ倍,隨后將其分別放置在n個不同節點中,其中同一個的編碼數據塊不能出現在一個節點中.

2 基于Hadamard 矩陣構造異構部分重復碼

本節基于Hadamard 矩陣構造存儲容量不同的異構部分重復碼.首先選一個4s(s=1,2,3,···)階的Hadamard矩陣,再將此Hadamard 矩陣進行簡單變換即可得到所需矩陣.將編碼數據塊與矩陣進行類比聯系,分布式存儲系統中的節點對應矩陣的行,而不同的編碼塊對應于矩陣的列.根據Hadamard 矩陣,引出存儲容量不同的異構FR 碼一般性構造算法,其具體步驟如下:

步驟1.首先采用(n,k)MDS 編碼(n≥k)對原始文件進行編碼,得到n個編碼數據塊c1,···,ck?1,ck,ck+1,···,cn,其中包括k個原始數據塊和n?k個校驗數據塊[6];

步驟2.取一個n+1階 標準型Hadamard 矩陣Hn+1(n+1為4的倍數),由式(1)對Hn+1進行簡單變換:

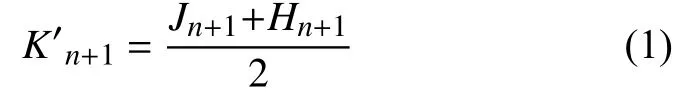
矩陣Jn+1中 元素全為1,Hn+1為標準Hadamard 矩陣,得到的K′n+1(n≥k)是一個0-1 矩陣,將K′n+1的第一行和第一列同時刪去得到所需矩陣Kn;

步驟3.將矩陣Kn中第j列出現的第(j+1)mod個1 改為0 得到新的矩陣Kn1,然后計算式(1):

其中,j=1,2···,n,i表示第i個FR 節點,aij表示矩陣第i行第j列的值.其中表示異構FR 碼的存儲節點,將矩陣Kn1中第i行中全部的1 所分別對應的列數提取出來,即可得到一個節點Ni存儲的數據塊,得到節點存儲容量不同的異構FR 碼.

具體的,選取一個12 階的Hadamard 矩陣如圖1所示,對其按步驟2 操作得到11 階矩陣K11如圖2所示,每一列的第個1 改為0 得到新的矩陣K111如圖3所示.隨后節點對應矩陣的行,而不同的編碼塊對應于矩陣的列.所以我們得到了存儲容量不同的異構的FR 碼,每個節點的存儲結構如圖4所示,其節點的存儲容量d=3,4,5,編碼塊的重復度 ρ=4.

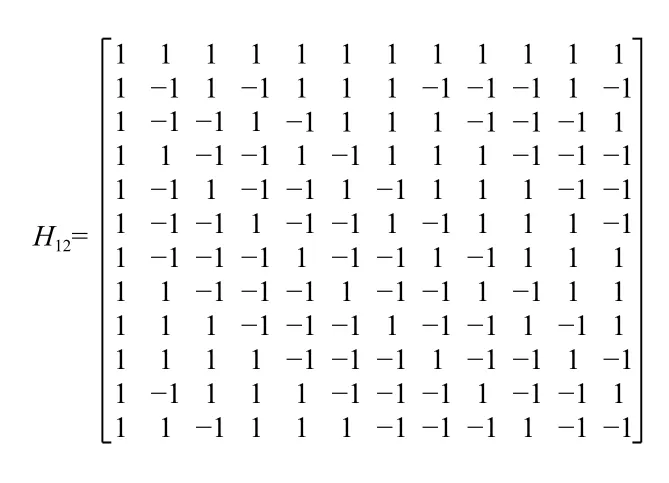
圖1 12 階Hadamard 矩陣

圖2 K11 矩陣

圖3 K111 矩陣

單個節點發生故障時,可以根據存活的其他節點直接下載所需的數據,即可恢復故障節點.例如在圖4中,若第二個節點N2發s生故障,通過下載節點N7恢復數據塊5和11,下載N9恢復數據塊3和7,即可完成節點N2的恢復;同時也可以根據節點N3>,N8>,N11分別下載數據塊3,5,7,11,也可完成故障節點N2的恢復.單節點發生故障可采用多種方式來恢復,同時也實現故障節點的精確無編碼修復.當兩個節點發生故障時,方法同一個故障節點修復.

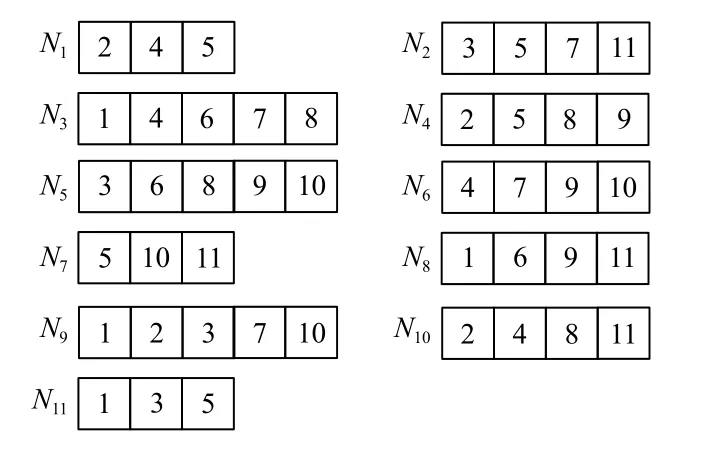
圖4 存儲容量異構的FR 碼節點存儲結構圖

3 可擴展的異構部分重復碼

本小節提出一種基于[7,3,4]簡單圖形構造可擴展異構部分重復碼的算法,此算法可以簡單對部分重復碼進行擴展,如現有結構不滿足已有需求需要進行擴容,則不需破壞已有的結構,只需在圖形尾部直接旋轉拼接圖形擴展,使得FR 碼可擴展,具體構造步驟如下所示:

步驟1.首先采用(n,k)M DS 編碼(n≥k)對原始文件進行編碼,得到n個編碼數據塊c1,···,ck?1,ck,ck+1,···,cn,其中包括k個原始數據塊和n?k個校驗數據塊[6];

步驟2.取一個[7,3,4]簡單圖形,如圖5所示.

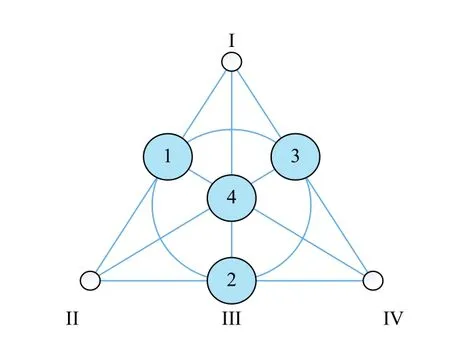
圖5 [7,3,4]簡單代碼圖形

步驟3.通過 [7,3,4]簡單圖形構造FR 碼:將外圍3 個頂點當作存儲節點,將內部的4 個頂點當作數據塊,數據塊按照順時針存放,臨近存儲節點的3 個數據塊存放在該存儲節點.

將 [7,3,4]簡單圖形的外圍3 個頂點當作存儲節點,將[7,3,4]簡單圖形內部的4 個頂點當作數據塊,數據塊按照順時針存放,臨近存儲節點的3 個數據塊存放在該存儲節點.

步驟4.通過將 [7,3,4]簡單圖形旋轉拼接構造可擴展FR 碼:

1)將擴展的[7,3,4]簡單圖形的外圍羅馬數字代表一個節點,外圍的第i個點表示分布式存儲系統中的第i個存儲節點Ni,共有n個 存儲節點(i=I,II,···,n);將與存儲節點直接相連的數據塊當作該存儲節點存放的數據塊,即可得到存儲容量和重復度異構的FR 碼.

2)當數據塊n=3t+4 時,需要t+1個 [7,3,4]簡單圖形旋轉拼接,構造出具有t+3個 存儲節點,n個數據塊的FR 碼.當數據塊n=4+3t+s(s=1,2)時,需要t+2個[7,3,4] 簡單圖形旋轉拼接,構造出具有t+3個存儲節點,n個數據塊的FR 碼.

若構造一個具有6 個存儲節點,13 個數據塊的FR碼.可將基本圖形翻轉拼接3 次,得到如圖6所示圖形,按上述方法可得到6 個存儲節點所存放的數據塊,如圖7所示,若當前結構無法滿足需求,可對其進行擴展,直至滿足需求,而且無需改變現有結構,如圖8所示.

圖6 圖形結構

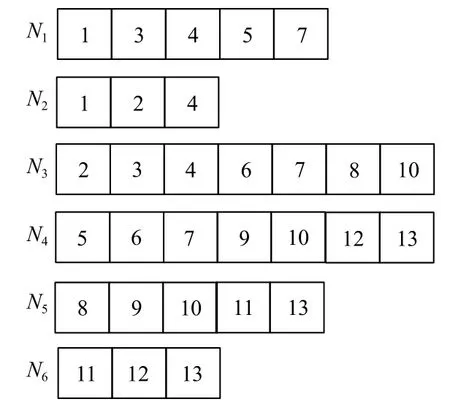
圖7 FR 碼節點存儲結構圖

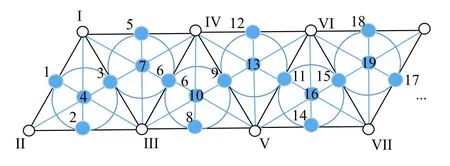
圖8 擴展圖形結構

可以看出共有6 個存儲節點.存儲節點N1和N5的存儲容量是5,存儲節點N3和N4的存儲容量是7,并且重復度 ρ為2 或3的一個異構的FR 碼.

當單個節點發生故障時,如圖7中,當第二個節點N2發生故障時,通過下載節點N1恢復數據塊1和4,下載N3恢復數據塊2,來完成節點N2的恢復;當節點N3發生故障時,通過下載節點N1恢復數據塊3,4和7,下載N2恢復數據塊2,下載N4恢復數據塊6和10,下載N5恢復數據塊8,即可完成節點N3的恢復.具體修復方式可選擇性較大,同時實現故障節點的精確無編碼修復.

4 性能分析

本小節對基于Hadamard 矩陣構造存儲容量異構的部分重復碼和基于[7,3,4]簡單圖形構造可擴展的異構部分重復碼進行性能分析,主要考慮修復帶寬開銷和修復局部性方面的性能,并與常見的RS 編碼進行性能比較.為了便于比較,基于Hadamard 矩陣構造存儲容量異構的部分重復碼算法選取(11,9)FR 碼,基于[7,3,4]簡單圖形構造可擴展異構部分重復碼的算法選取(13,9)F R 碼,取M=1000 Mbit.

4.1 修復帶寬開銷

修復帶寬開銷指的是恢復失效節點時下載的數據量大小.例如采用(11,9)RS 編碼,由于RS 編碼恢復故障節點需要下載全部原文件,所以修復帶寬開銷為η=M;采用基于Hadamard 矩陣構造存儲容量不同的異構部分重復碼構造(11,9)FR 碼時,發生節點故障時的修復帶寬開銷為η=3M/k,5M/k或者7M/k.為便于比較,本文選取中間值作為代表值.在采用基于[7,3,4]簡單圖形構造可擴展異構部分重復碼的算法構造(13,9)FR 碼時,發生節點故障的修復帶寬開銷為η=3M/k,5M/k或者 7M/k,而采用(13,9)RS 編碼時,發生節點故障的修復帶寬開銷為η=M.由于圖形特殊構造,隨著節點增多修復帶寬開銷基本都是7M/k,所以選取其為代表值.以上2 項數據與RS 碼仿真對比如圖9所示.

經過對比不難發現本文提出的兩種異構部分重復碼構造的算法,節點發生故障時修復帶寬開銷比RS 編碼明顯降低.當節點數少于16 時,基于Hadamard 矩陣構造的異構FR 碼修復帶寬開銷小于基于[7,3,4]簡單圖形構造異構FR 碼.但是當節點數逐漸增大,基于[7,3,4]簡單圖形構造異構FR 碼的修復帶寬開銷小于基于Hadamard 矩陣構造的異構FR 碼.

4.2 修復局部性

發生節點故障時需要連接的存活節點數目稱為修復局部性.當發生單節點故障時,(11,9)RS 編碼需要連接9 個節點恢復原文件用以修復故障節點,修復局部性為9;而基于Hadamard 矩陣構造存儲容量異構的FR 碼構造的(11,9)FR 碼,單節點故障時需要連接2 個或者3 個節點來修復,故修復局部性為2 或者3.

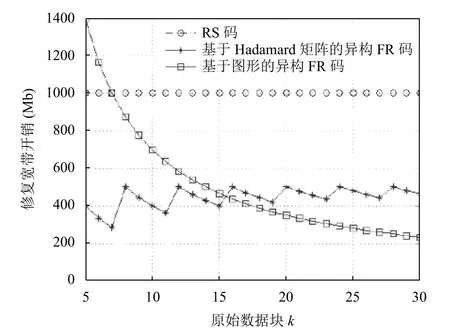
圖9 修復帶寬開銷對比

采用基于[7,3,4]簡單圖形構造可擴展異構部分重復碼的算法構造(13,9)FR 碼時,發生節點故障時需要連接2,3 或者4 個節點來恢復故障節點,所以修復局部性為2,3 或4;而(13,9)RS 碼發生單節點故障時,RS碼修復局部性為9.

分析發現修復單個故障節點時,基于Hadamard 矩陣構造存儲容量異構的FR 碼和基于[7,3,4]簡單圖形構造可擴展異構FR 碼的修復局部性,優于RS 編碼的修復局部性.但是[7,3,4]簡單圖形構造的異構FR 碼無法修復多節點故障,是下一步研究的方向.

5 結論

本文提出基于Hadamard 矩陣和[7,3,4]圖形分別構造異構的部分重復碼的一般算法.與現有的FR 碼相比,采用Hadamard 矩陣和[7,3,4]圖形構造FR 碼更加簡潔明了,其中基于Hadamard 矩陣可實現由同構經過簡單變換為異構編碼方式;基于[7,3,4]圖形構造FR 碼可實現擴展延升,若當前結構無法滿足需求,可對其進行擴展,直至滿足需求,且無需改變現有結構.經過與RS 碼理論分析對比發現,設計的兩種異構FR 碼的修復局部性、修復帶寬開銷進一步降低,性能進一步提高.