Gerhards模型在針葉木材長期壽命預測中的適用性分析*

王忠鋮 楊 娜

( 北京交通大學土木建筑工程學院 結構風工程與城市風環境北京市重點實驗室 北京 100044)

木材的長期承載能力遠低于暫時承載能力，在長期荷載作用下，木材會發生纖維等速蠕滑,累積后產生較大變形，強度降低，且施加荷載越大，木材從受荷開始至破壞的時間越短(龍衛國， 2005)。20世紀50—80年代，國外學者對木材長期強度進行了大量試驗研究(Brokawetal.， 1952； Youngsetal.， 1963； James， 1968； Mcnatt， 1975； Strickleretal.， 1976)，基于金屬疲勞破壞的Miners準則(Schijve， 2014)提出一種線性累積損傷理論，用以解釋木材長期受荷作用下強度降低的現象(Gerhards， 1979)，即Gerhards模型：

(1)

式中：σ(t)為外應力；fs為木材靜力強度；α為損傷累積量，其變化范圍為[0，1]，α=0表示木材無損傷，α=1表示木材失效；A、B為待擬合參數。

Gerhards模型形式簡單，以往眾多木材長期受荷性能研究均以該模型為基礎(Fridleyetal.， 1989； 1990； 1991； Kuilen， 2007； 李瑜， 2008； Srensenetal.， 2005； 瞿偉廉等， 2008； Qinetal.， 2017； Wangetal.， 2019)； 然而，所有基于Gerhards模型的木材壽命預測研究，均普遍存在模型參數選取問題，Gerhards模型是一個指數形式的函數，參數的微小差異會導致壽命預測結果的巨大差別(Wangetal.， 2019)。

鑒于此，本研究分析木材長期壽命預測中常用Gerhards模型的適用性，探討參數選取對不同加載工況下模型預測結果的影響，同時針對木材壽命預測中預測值大于真實值的問題，提出一種基于Gerhards模型的區間預測模型分析方法，以期為進一步提高木材長期壽命預測精度提供理論依據。

1 Gerhards模型的適用性分析

1.1 Gerhards模型與Gerhards試驗對比

Gerhards模型的數學表達式最早由Gerhards(1979)提出，隨后其開展了包含6種工況的北美花旗松(Pseudotsugamenziesii)四點彎曲線性加載和恒定加載試驗(Gerhards試驗)(Gerhardsetal.， 1987)，木材試樣橫截面尺寸約50 mm×100 mm(寬×高)，跨度約2 100 mm，試驗期間環境溫度24 ℃，相對濕度55%，各試驗加載工況見表1。

表1 Gerhards試驗的加載工況①Tab.1 Loading conditions of Gerhards’s experiment

Gerhards試驗獲得了不同線性加載速率和恒定加載量級下的木材破壞時間，對不同加載工況進行組合，共擬合得到8組Gerhards模型參數A和B，見表2。

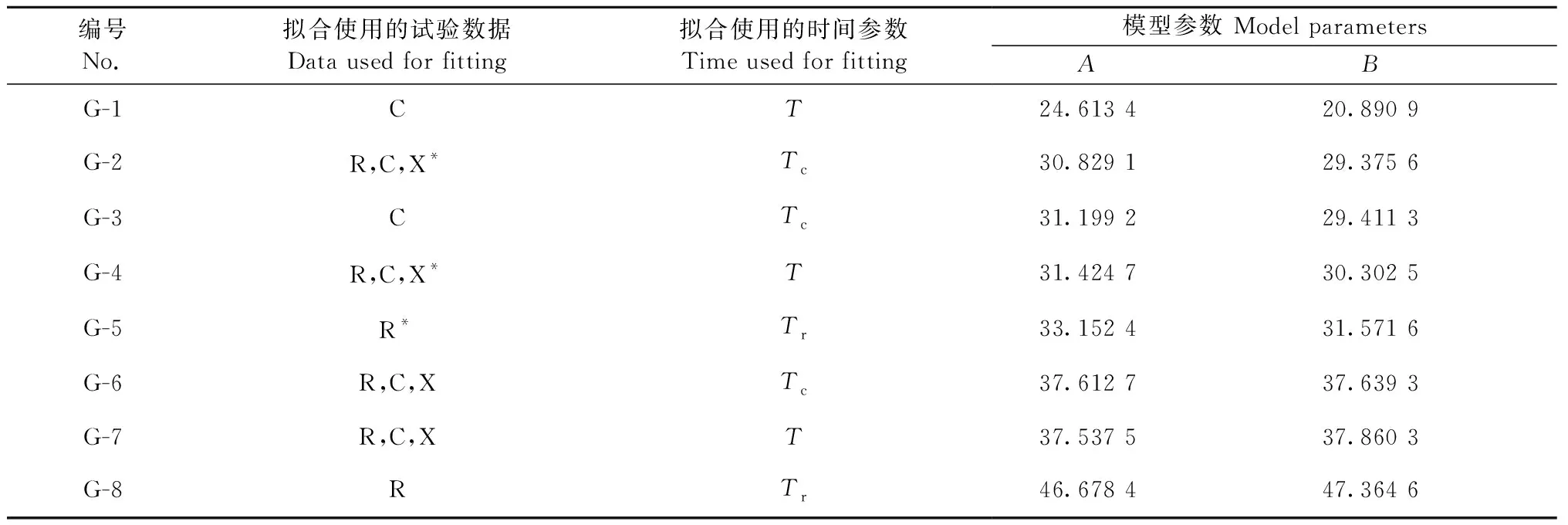
表2 Gerhards模型的8組模型參數①Tab.2 8 sets of model parameters of Gerhards model

Gerhards模型參數擬合自Gerhards試驗數據，由于各模型參數源于不同加載工況組合，因此本研究首先分析Gerhards模型在預測Gerhards試驗6種工況時的適用性。

對式(1)積分，可推導出木材破壞時間FD(failure duration)(min)與線性加載速度k(N·min-1)或恒定應力水平SL(stress level)的關系：

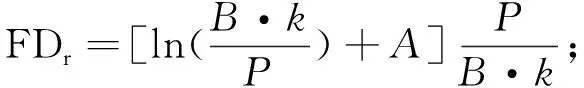
(2)

FDc=exp(A-B·SL)。

(3)

式中：P為單位換算系數，P=3 168.89； FDr、FDc分別為線性加載和恒定加載木材破壞時間。

將8組Gerhards模型參數代入式(2)和(3)，計算出各模型對各工況試樣破壞時間的預測值見表3，其中各工況下試樣破壞時間的中位數參考Gerhards等(1987)。

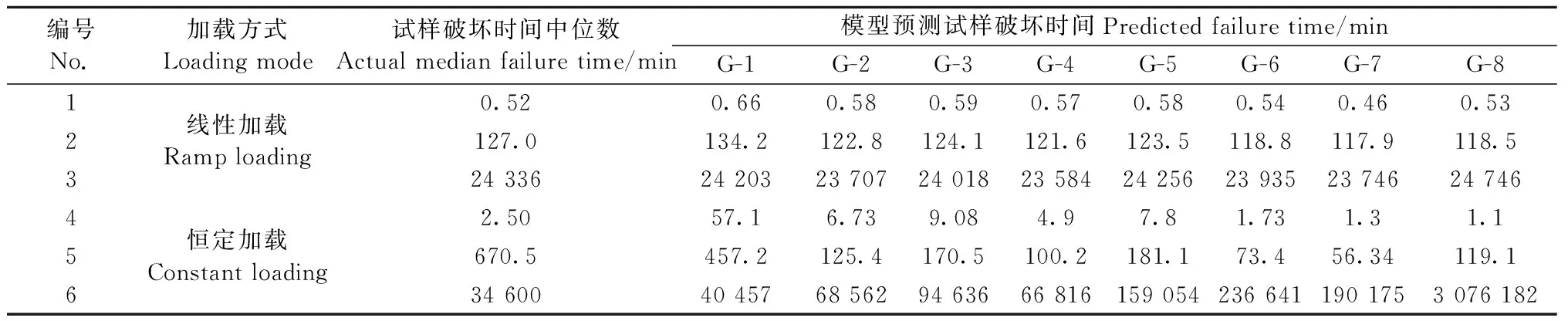
表3 Gerhards試驗中試樣破壞時間中位數與各模型預測值對比Tab.3 Comparison between actual median failure time of Gerhards’s experiment and predicted failure time

由表3可知，8組Gerhards模型在預測線性加載的3種工況時，各模型預測值接近，且與試驗值偏差較小。對于工況1，模型預測誤差的最小值和最大值分別為1.92%(G-8)和27.92%(G-1)； 對于工況2，模型預測誤差的最小值和最大值分別為2.28%(G-3)和7.17%(G-7)； 對于工況3，模型預測誤差的最小值和最大值分別為0.33%(G-5)和3.09%(G-4)。8組Gerhards模型在預測恒定加載的3種工況時，各模型預測精度普遍低于線性加載工況。對于工況4，模型預測誤差的最小值和最大值分別為30.80%(G-6)和2 184.00%(G-1)； 對于工況5，模型預測誤差的最小值和最大值分別為31.81%(G-1)和91.60%(G-7)； 對于工況6，模型預測誤差的最小值和最大值分別為16.93%(G-1)和8 790.70%(G-8)。由此可見，與線性加載工況相比，恒定加載工況下各模型預測值間差別較大，且個別模型預測值與試驗值差異極大。這是因為Gerhards模型在預測線性加載工況時，FD與k為乘積關系(式2)，而在預測恒定荷載工況時，FD與SL為指數關系(式3)，參數的微小差異會導致預測結果的巨大差別。實際服役過程中，木結構主要承受恒定荷載，因此基于Gerhards模型預測木材壽命前，必須明確各模型的適用范圍，否則會使木材壽命預測值遠大于真實值，預測結果偏于危險。

1.2 Gerhards模型與恒定荷載試驗對比

木結構構件所受SL普遍較小，構件壽命往往相對較長。本研究選取同樣為長期恒定荷載的2類針葉材試驗，即Wood和Hoffmeyer試驗數據進行對比(Wood， 1951； Hoffmeyeretal.， 2007)，以分析Gerhards模型在木材長期壽命預測中的適用性。

Wood試驗為抗彎試驗，用材為北美花旗松，試樣橫截面尺寸約50 mm×50 mm(寬×高)，含水率為6%和12%，SL介于60%～95%之間； Hoffmeyer試驗同樣為抗彎試樣，用材為歐洲云杉(Piceaabies)，試樣尺寸約1 800 mm×44 mm×95 mm(長×寬×高)，含水率為11%和20%，SL介于55%～105%之間。2類木材的基本物理力學性質見表4(龍衛國， 2005)。

表4 長期受荷試驗用2類針葉材的物理力學性質參考值Tab.4 Reference value of the physical and mechanical properties of the softwood used in the long-term load test

將8組Gerhards模型與Wood和Hoffmeyer試驗數據在“SL-lgFD”坐標系下對比，以反映預測曲線與試驗數據之間的關系(Wangetal.， 2019)，見圖1。

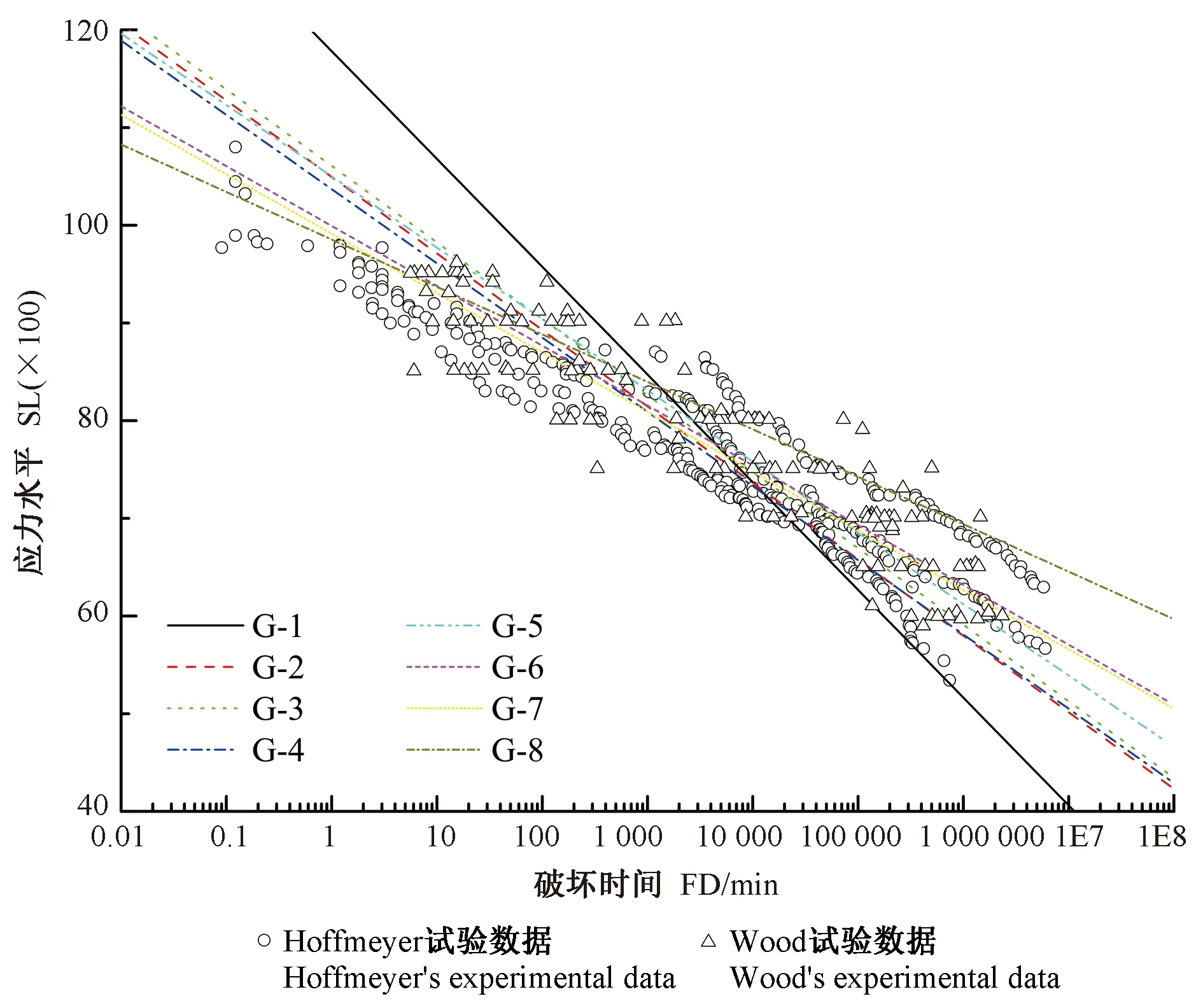
圖1 Gerhards模型與恒定載荷試驗數據對比Fig. 1 Comparison between Gerhards model and constant experimental data

由圖1可知，除G-1模型外，其余模型均能較好穿過試驗數據點，模型對試驗值預測較好。對于G-1模型，當SL大于80%時，模型預測的破壞時間普遍大于試驗值； 當SL小于80%時，模型預測的破壞時間普遍小于試驗值。

為了量化各模型預測效果優劣，計算各模型對SL預測值與試驗值的均方誤差(mean square error，MSE)：

(4)

式中：xi為預測值；μ為試驗值；n為試驗數據總樣本量。

各模型預測效果的均方誤差見表5，其中Wood試驗數據與模型預測值之間的均方誤差參考Wang等(2019)。

表5 各模型對SL預測值與試驗值的均方誤差Tab.5 MSEs between predicted and experimental SLs

由表5可知，對于Wood長期恒定載荷試驗，G-5—G-8模型預測效果較好，G-2—G-4模型預測效果較差，G-1模型預測效果最差； 對于Hoffmeyer長期恒定載荷試驗，G-6—G-7模型預測效果較好，G-2—G-5和G-8模型預測效果較差，G-1模型預測效果最差。出現這種差異的原因在于各模型加載工況與被預測對象加載工況的相似程度。以Wood試驗為例，表6對比了Gerhards與Wood試驗中相似SL下試樣破壞時間。

表6 Gerhards與Wood試驗中相似SL下試樣破壞時間對比Tab.6 Comparison of median failure time under similar SL between Gerhards’s and Wood’s experiments

由表6可知，對于Gerhards試驗工況6，試樣破壞時間中位數與Wood試驗中相似SL下試樣破壞時間中位數差異極大； 而對于工況4、5，差異則相對較小。由此可見，在預測Wood試驗數據時，Gerhards模型中工況6數據占比越大，模型預測精度越低，因此G-1—G-4模型的預測效果劣于G-5—G-8模型。同理可分析Gerhards模型對Hoffmeyer試驗數據預測效果優劣的原因。

綜上所述，當木材試樣為承受SL介于60%～95%的北美花旗松時，建議采用G-6模型進行壽命預測； 當木材試樣為承受SL介于55%～105%的歐洲云杉時，建議采用G-7模型進行壽命預測； 當木材試樣承受SL小于50%時，建議采用G-1模型進行壽命預測。有研究曾對比8類木材【花旗松及其膠合木、臺灣柏(Juniperusformosana)、日本柳杉(Cryptomeriajaponica)、北美云杉(Piceasitchensis)、樺木(Betulaspp.)、楓木(Acerspp.)、圓果桉(Eucalyptuspilularis)，前5類屬于針葉材，后3類屬于闊葉材】試樣持續受荷試驗結果發現，盡管樹種、截面尺寸和含水率不同，但木材壽命與SL有很好的一致性(Pearson， 1972； 樊承謀等， 2008)。因此，當被預測木材樹種、尺寸和含水率與本研究分析使用的北美花旗松和歐洲云杉木試樣不同時，Gerhards模型預測值仍可作為參考。

2 基于Gerhards模型的SLC區間預測模型分析方法

由上述分析可知，當預測模型所用數據的加載工況與被預測對象的受荷工況相似時，模型具有較好預測效果，本研究稱這類基于相似工況試驗數據擬合的模型為SLC(similar loading condition)模型。由圖1可知，雖然Gerhards模型曲線穿過Wood和Hoffmeyer試驗數據點圍成的區域，但仍有相當一部分數據位于曲線左下方，即模型預測的試樣破壞時間極有可能大于試樣實際破壞時間，這對于木材壽命預測是偏危險的。鑒于此，本研究提出一種基于Gerhards模型的SLC區間預測模型分析方法，以改進木材長期壽命預測精度。

(5)

上述統計量匯總于表7。

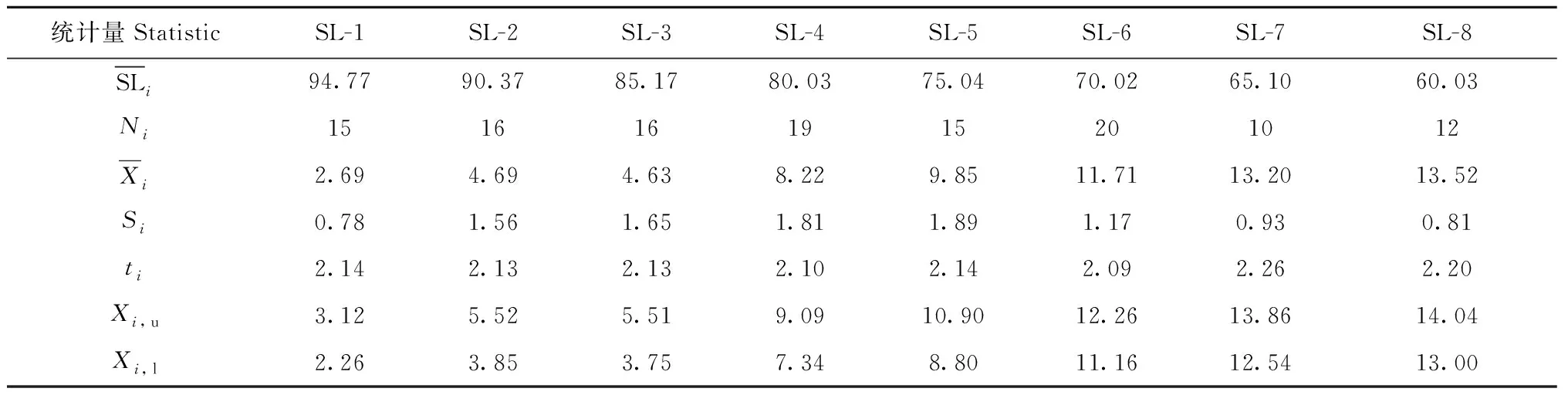
表7 Wood恒定載荷試驗數據的統計量Tab.7 Statistics of Wood’s experimental data

由式(3)可知，木材受恒定載荷時SL與FD存在以下關系：

SL=m-n·lnFD。

(6)

式中：m和n為待擬合參數。

由圖2可知，藍色虛線包絡區域為采用上、下限模型得到的壽命預測區間，因經過一次由lnFD到FD的計算，區間過度向均值模型曲線靠攏，導致仍有大量試驗點落在區間外。

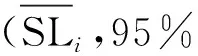
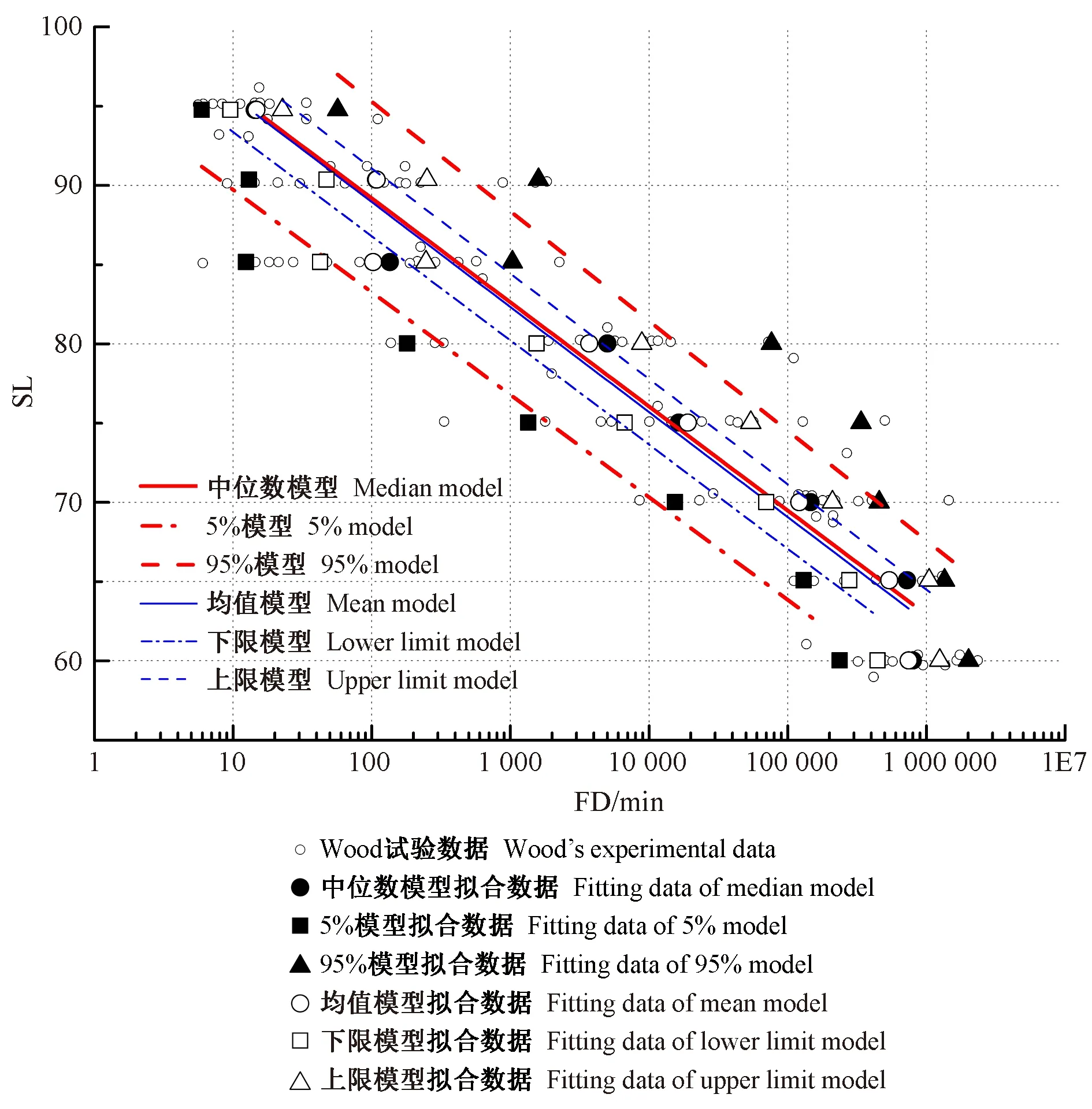
圖2 基于Wood試驗數據的區間預測模型Fig. 2 Interval prediction model based on Wood’s experimental data

以上2類區間模型表達式中的m、n統計于表8。

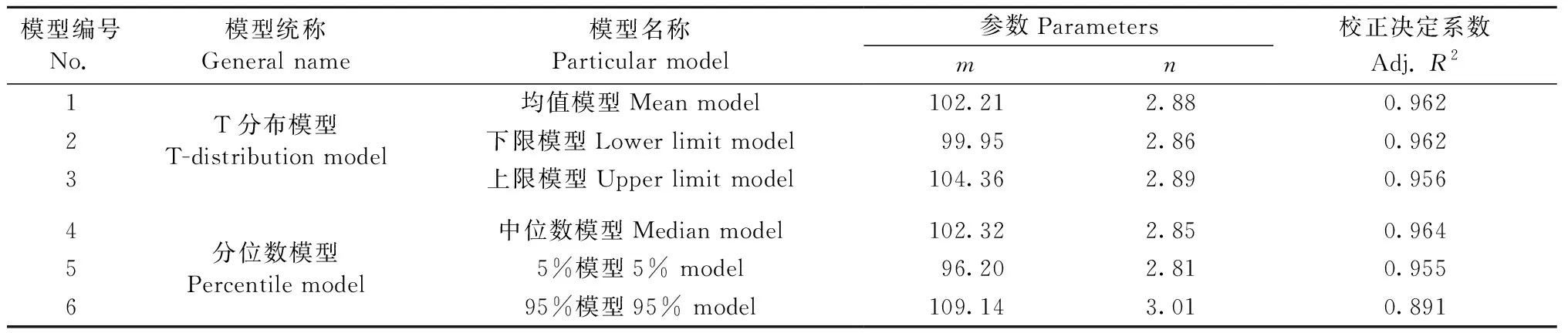
表8 基于Wood試驗數據的2類區間預測模型參數對比Tab.8 Comparison of parameters of two interval prediction model based on Wood’s experimental data

由圖2和表8可知，均值模型與中位數模型十分接近，說明T分布模型與分位數模型相對于試驗數據點的位置近乎同心，只是包絡寬度不同，使用分位數模型可使絕大部分試驗數據點落在區間模型內，從而避免壽命預測值大于真實值。因此，對于相似受荷試驗數據的情況，在木材壽命預測時建議參考本研究提出的基于Gerhards模型的SLC區間預測模型分析方法，以提高木材壽命預測精度。

3 結論

1) 不同工況組合擬合得到的模型具有不同適用范圍，不加區分地應用模型會使木材壽命預測精度大幅降低。以對Gerhards試驗數據的預測結果為例，各Gerhards模型對線性加載工況下木材壽命預測值較為接近，預測結果較為精確，預測誤差介于0.33%～27.92%之間； 各Gerhards模型對恒定荷載工況下木材壽命預測值差異較大，預測精度較差，預測誤差介于16.93%～8 790.70%之間。

2) G-6模型適用于SL介于60%～95%的北美花旗松壽命預測，G-7模型適用于SL介于55%～105%的歐洲云杉壽命預測，SL小于50%建議采用G-1模型進行壽命預測。當被預測木材樹種、尺寸和含水率與本研究分析使用試樣不同時，Gerhards模型預測值仍可作為參考。

3) 當預測模型所用數據加載工況與被預測對象受荷工況相似時，模型具有較好預測效果。SLC區間預測模型可有效避免模型預測壽命大于木材實際壽命的問題，基于試驗數據分位數擬合的預測模型較基于T分布假設擬合的預測模型涵蓋更多試驗數據點。

需要注意的是，木材是一種生物建材，與其他常用建筑材料相比，木材力學性能的離散性相對較大，因此，木材力學性能本身差異同樣可能導致Gerhards模型預測值與試驗值之間的差異。此外，本研究采用的試驗數據均為隔離環境因素影響的北美花旗松和歐洲云杉實驗室數據，模型預測值較真實環境中的木材壽命可能存在一定偏差，但對受環境影響較小的室內木結構木材壽命預測仍具有一定參考價值。更進一步地精確預測木材壽命，可在本研究分析Gerhards模型的基礎上考慮各種環境因素的影響，或直接采用SLC區間模型分析方法對包含環境因素影響的試驗數據進行擬合，進而得到更為精確預測真實環境中木材壽命的模型。