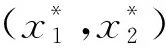一類指數型非線性隨機差分方程組解的穩定性分析

佘智鳳, 廖新元, 陳沙沙, 金 薇

(南華大學 數理學院, 湖南 衡陽 421001)

0 引 言

眾所周知，大自然中事物的發展都有其客觀規律，最開始，人們用確定性模型來刻畫系統。實際上，世界的本質是隨機的，這些系統受到自然界多種因素的影響，有些影響比較大，不可忽略，1953年，杜布出版了名著《隨機過程論》，系統地敘述了隨機過程基本理論。

隨機差分方程由于考慮了現實世界多種因素對系統的影響，較之確定性方程，能更準確地描述實際生活中的現象和實物發展的客觀規律，這促使國內外學者紛紛投入研究，并取得了豐富的研究成果，此后隨機差分方程的研究工作迅速發展。隨機差分方程在經濟學、生物學、地質學和物理學等各個領域中都有廣泛的應用[1-9]。

對有些問題的研究，線性隨機差分方程不能準確地描述實際動力學性態，具有一定的局限性，為了便于研究，許多學者建立了指數型差分方程[10-16]。但忽略了自然界中各種隨機擾動的存在，相較而言，指數型非線性隨機差分方程更貼切于現實情況。例如，文獻[17]中，L.Shaikhet在指數型離散時滯蚊子種群方程的基礎上，考慮了隨機擾動對系統的影響，研究了指數型隨機蚊子種群方程在平衡點處依概率穩定的充分條件。本文在其基礎上，考慮了雙隨機擾動，研究其類似的方程組系統平衡解穩定的充分條件。

1 正平衡點

本文考慮下列指數型非線性隨機差分方程組系統平衡解穩定的充分條件

n=0,1,2，……,x1(j)=φ1(j),

x2(j)=φ2(j),j=-1,0。

(1)

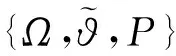
Eξk(n)=0,E2ξk(n)=0,Eξi(n)Eξj(n)=0,

i,j=1,2,3,4,i≠j。

首先求解模型正平衡點存在的參數條件及正平衡點滿足的條件。

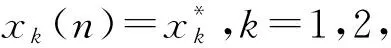
(2)

顯然，對任意的正參數，即a,b,c,μ,v>0，方程(1)都有零解E0=(0,0)。

(3)

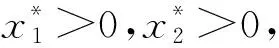
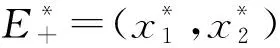
(4)

(5)

(6)

證明 1) 由方程組(2)可得

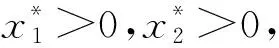
則

即η>1。

2)顯而易見，條件(4)直接由方程組(2)得到。

3)將式(4)中第2個式子代入方程組(2)第2個式子得到(5)第1個式子,將(4)中第1個式子代入(2)第1個式子得到(5)第2個式子。

4)由式(4)2個式子分別可得

即

條件(6)得證。

2 線性化和一些引理

(7)

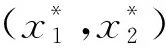
(8)

對于零平衡點E0,方程(7),(8)分別可寫成

(9)

(10)

為了研究方程在零平衡點處的穩定性，先給出下列引理。

記σ-代數Fi的條件期望為Ei=E{./φi}，令Uε=x:|x|≤ε,ΔVi=Vi+1-Vi。

引理2[21]對方程(7)(或(9))，假設存在一個非負函數Vi=V(i,z(-1),……,z(i))滿足下列條件

V(i,y(-1),……,y(i))≥c0|y(i)|2,

(11)

V(0,φ(-1),……,φ(0))≤c1‖φ‖2,

(12)

EiΔVi≤0,xj∈Uε,-h≤j≤i,i∈Z。

(13)

其中ε>0,c0>0,c1>0，則方程(7)(或(9))的平凡解是依概率穩定的。

引理3[21]對方程(8)(或(10))，假設存在一個非負函數Vi=V(i,z(-1),……,z(i))滿足條件(12)且

EiΔVi≤-c2E|z(i)|2,i∈Z。

(14)

其中c2>0，那么方程(8)(或(10))的零解是漸近均方穩定的。

備注1：對于一個高階非線性差分方程組，若其線性化方程存在一個泛函Vi滿足條件(11)、(12)和(14)，那么其初始非線性方程組也存在一個泛函Vi滿足條件(11)、(12)和(13)。為了得到非線性方程(7)(或(9))零解依概率穩定的充分條件，只需要通過構造滿足條件(11)、(12)和(14)的泛函Vi以得到其線性化方程(8)(或(10))零解漸近均方穩定的充分條件。

3 穩定性條件

下面引進一個二維線性隨機差分方程組

(15)

顯然，方程(15)是方程(7)和(9)的更一般化的形式，則方程(15)零解漸近均方穩定的的充分條件也適用于方程(7)和(9)，為了得到方程(15)零解漸近均方穩定的充分條件，令

Q,D,U是對稱矩陣，若對于兩個對稱矩陣Q,D，Q-D是一個正定矩陣，則記Q>D。

定理1設對于某些正定矩陣Q,矩陣方程A′DA-D=-U有半正定解D，使得

那么方程(15)的零解是漸近均方穩定的。

證明 記

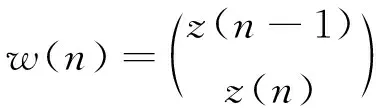
那么式(15)可以寫成

w(n+1)=[A+B(ξ(n+1))]w(n)

構造Lyapunov函數V(n)=w′(n)Dw(n),則

EΔV(n)=E(w′(n+1)Dw(n+1)-

w′(n)Dw(n))=Ew′(n)([A+

B′(ξ(n+1))]D[A+B(ξ(n+1))]-

D)w(n)=Ew′(n)[A′DA-D+

B′(ξ(n+1))DB(ξ(n+1))]w(n)=

Ew′(n)[-U+B′(ξ(n+1))DB(ξ(n+

1))]w(n)=ETr(w(n)w′(n))[-U+

B′(ξ(n+1))DB(ξ(n+1))]=

TrE(w(n)w′(n))[-U+B′(ξ(n+

1))DB(ξ(n+1))]=Tr(E(z(n)×

z′(n))[-Q+Eθ′(ξ(n+1))×

D22θ(ξ(n+1))])=Tr(E(z(n)×

z′(n))[-Q+Eθ′(ξ(n+1))×

D22θ(ξ(n+1))])=Tr(E(z(n)×

z′(n))[-Q+Eθ′(ξ(n+1))×

D22θ(ξ(n+1))])=Tr(E(z(n)×

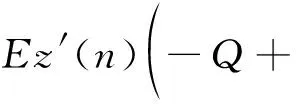
綜上，EΔV(n)≤-cE|z(n)|2,由引理3可得，方程(15)的零解是漸近均方穩定的。

備注2：對方程(10)(或(8))，如果定理1的條件成立，則方程(10)(或(8))的零解是漸近均方穩定的，由備注1,可以得到，方程(9)(或(7)的零解是依概率穩定的，因此方程(1)的平衡點依概率穩定的充分條件得證。

4 數值模擬

1)令a=0.6,b=0.15,c=0.45,d=0.2,μ=ν=0.25,此時η<1，則方程(1)只有零解E0，當

由矩陣方程A′DA-D=-U，得

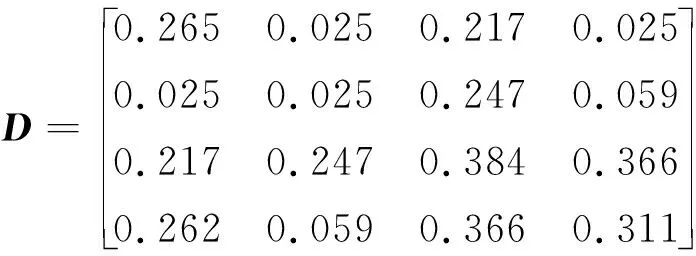
由引理2,引理3和定理1可得：

1)方程(10)的零解是漸近均方穩定的；

2)方程(9)的零解是依概率穩定的。

考慮方程(9),即考慮方程(1)解的軌跡。令σ11=0.11,σ12=0.25,σ21=0.31,σ22=0.11,y1(-1)=0.5,y1(0)=0.4,y2(-1)=0.6,y2(0)=0.8。如圖1所示，根據方程(9)的零平衡點的依概率穩定性，其100個解的軌跡都趨向于零。

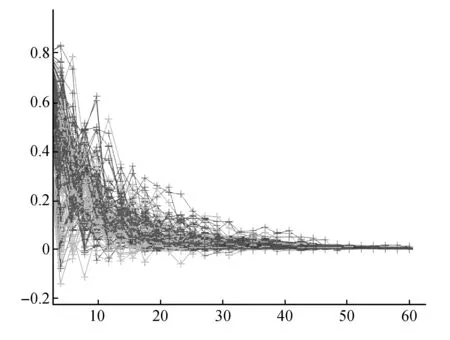
圖1 方程(9)解的100個軌跡Fig.1 100 trajectories of the solution of the system(9)

2)令a=0.9,b=0.15,c=0.7,d=0.45,μ=ν=0.25,則η=2.25>1，方程(1)不僅有零平衡點E0還有正平衡點E+=(0.287,0.334)，考慮方程(1)的正解，當

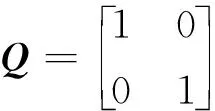
由矩陣方程A′DA-D=-U，得

由引理2,引理3和定理1可得：

1)方程(8)的零解是漸近均方穩定的；

2)方程(7)的零解(方程(1)正平衡點)是依概率穩定的。

考慮方程(9)也就是考慮方程(1)解的軌跡。令σ11=0.15,σ12=0.21,σ21=0.11,σ22=0.25,y1(-1)=0.5,y1(0)=0.4,y2(-1)=0.6,y2(0)=0.8根據方程(9)的零平衡點的不穩定性，其解的軌跡如圖2所示。

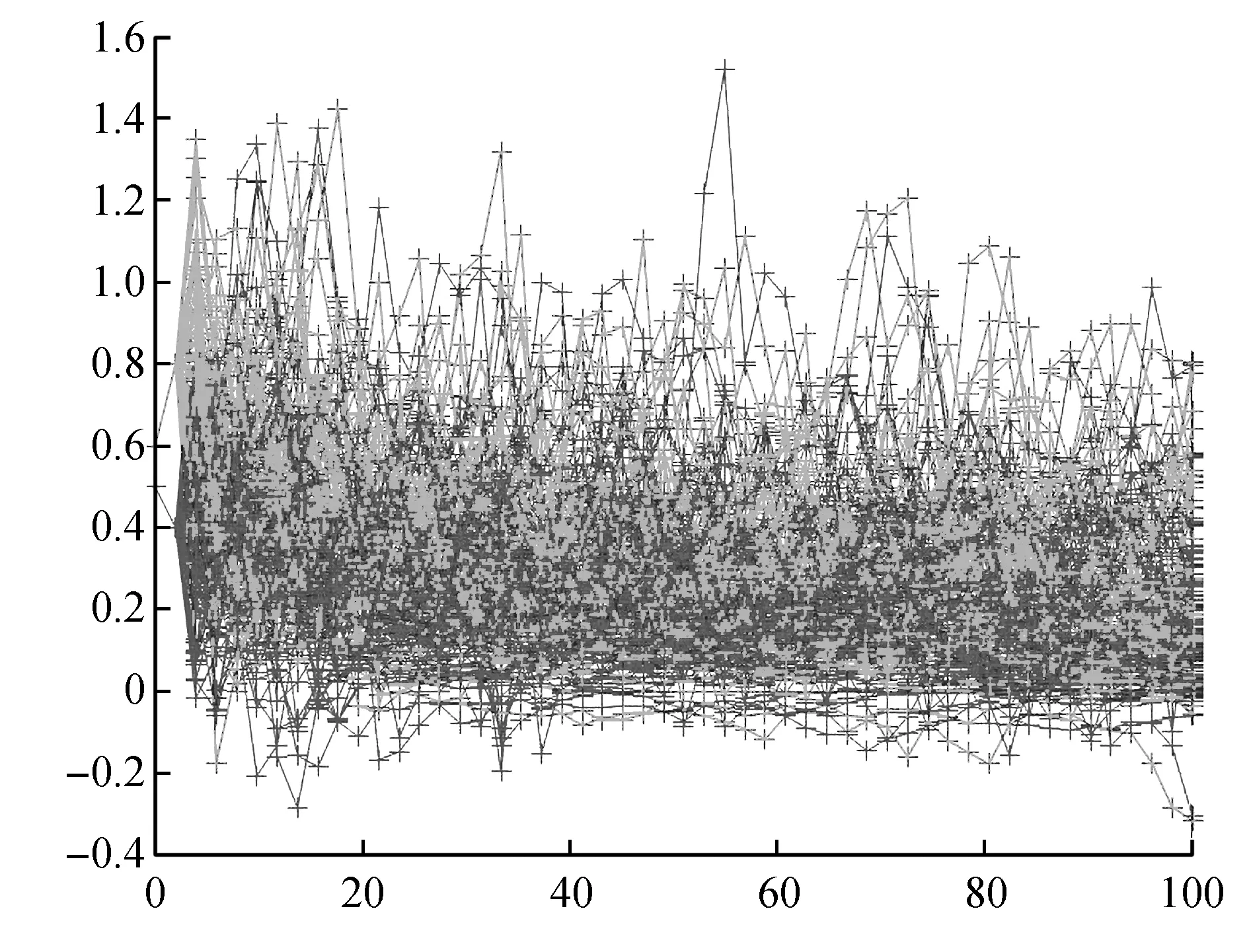
圖2 方程(9)解的100個軌跡Fig.2 100 trajectories of the solution of the system(9)

考慮方程(1)的零解，當

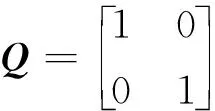
由矩陣方程A′DA-D=-U，可得d11=0.097,d22=-0.127,d33=-5.645,d44=0.481,則矩陣D不是一個正定矩陣，方程(1)的零解是不穩定的。

考慮方程(1)解的軌跡，設方程(1)的初值函數為x1(-1)=0.5,x1(0)=0.6,x2(-1)=0.4,x2(0)=0.8,σ11=0.11,σ12=0.15,σ21=0.13,σ22=0.11,方程(1)的正平衡點是依概率穩定的，如圖3所示，方程(1)的解的軌跡都收斂于正平衡點E+=(0.287,0.334)。

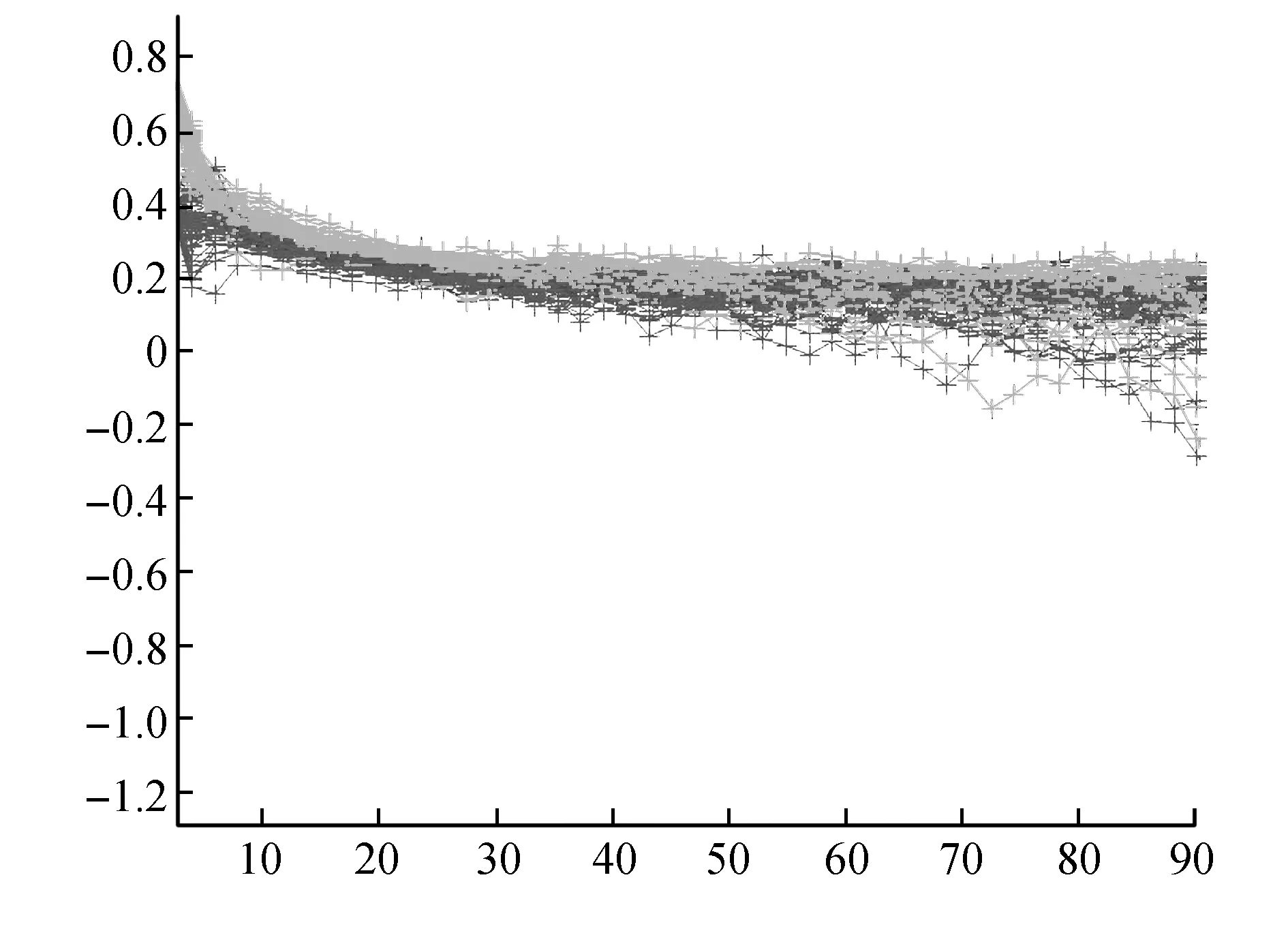
圖3 方程(1)解的100個軌跡Fig.3 100 trajectories of the solution of the system(1)

5 結 論