汽泡活化核心密度預測模型分析

何雯， 趙陳儒， 薄涵亮

(清華大學 核能與新能源技術研究院， 北京 100084)

沸騰換熱與汽泡行為息息相關，完整的換熱過程通常包括汽泡的核化、生長、脫離和浮升[1]。活化核心密度表示單位面積內汽泡核化的數量，直接影響汽泡蒸發帶走的熱量，因此具有較大的研究意義。影響活化核心密度Na的因素很多。文獻[2]主要考慮了壁面過熱度、壓力和接觸角的影響，通過理論分析提出了一套預測模型；Basu等[3]認為接觸角和壁面過熱度的影響最大，因此以過熱度15 ℃為界，提出一套預測模型；Ren等[4]和Ai等[5]分別對過冷流動沸騰下的汽泡行為開展了實驗研究，預測模型主要考慮了液體過冷度、質量流速和壁面過熱度等的影響。可見，目前預測活化核心密度的預測模型以及考慮的影響因素很多，但這些模型的準確度還有待進一步分析。此外，汽泡從壁面的凹坑處核化，目前的實驗大多采用統計法預測活化核心密度，但基于的前提是凹坑分布均勻。然而，Yang等[6]通過電子顯微鏡發現汽泡在成核表面呈現某種概率分布；Qi等[7]和Zou等[8]同樣發現這一規律，并推薦采用泊松分布對其進行描述。文獻[1-8]主要針對汽泡成核的空間分布，目的在于讓活化核心密度的統計更加準確，但是沸騰本身非常復雜，由于沸騰引起的不穩定性，如Klausner等[9]發現在流動沸騰下壁面過熱度呈正態分布，依然會造成汽泡動力學參數呈現概率分布。目前，關于脫離直徑在不同沸騰工況下的概率分布研究較多[10-11]，但是關于活化核心密度的研究基本沒有，用于描述的概率分布函數還有待進一步確定。

活化核心密度對于換熱計算非常重要，為對其進行更準確地描述，本文利用現有實驗數據，首先對活化核心密度的影響因素進行分析，再對現有預測模型的準確度進行對比和分析，最后對活化核心密度的概率分布進行初步研究。

1 影響因素分析

1.1 現有實驗數據

沸騰通常可分為池沸騰和流動沸騰，為在更大范圍內對活化核心密度預測模型的準確性進行分析，從8組獨立實驗中選取698個實驗數據點，其中流動沸騰共412個[3-5,12-15]，壓力P數據范圍為0.101～0.312 MPa，接觸角θ為5°～81°，液體過冷度ΔTsub為0～50 K，壁面過熱度ΔTsup為0.6～37 K，質量流速G為86～1 909 kg/m2s；池沸騰共286個數據點[3,16]，數據范圍為P為0.101～19.8 MPa，接觸角θ為30°～90°，壁面過熱度ΔTsup為1.8～18.8 K。由于流動沸騰壓力范圍相對較小，因此活化核心密度Na數值范圍為0.9～53.0/cm2，池沸騰Na范圍為1.0～1.5×106/cm2。

1.2 影響因素

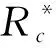
(1)

式中：Tsat表示飽和溫度；hfg表示汽化潛熱；ΔTsup表示壁面過熱度；σ和ρg分別表示表面張力和氣相密度。可見，Na直接受物性和壁面過熱度的影響，并且壁面過熱度越大，臨界半徑越小，汽泡越容易在壁面核化，Na越大。此外，根據汽泡吸附準則[17]，只有當凹坑頂部的錐角小于0.5倍液體和固體之間的接觸角時，該凹坑才能吸附汽泡。可見，接觸角越大，越有利于汽泡的產生。而對于壓力的影響，Borishanskii等[16]通過實驗研究了0.101～19.8 MPa下Na隨壁面過熱度的變化情況。結果表明：當壓力較低時，Na同時隨壁面過熱度和壓力的增大而增大，而當壓力進一步增大后(大于7.3 MPa)，壁面過熱度的影響減弱。可見，Na和壓力、接觸角、壁面過熱度均呈正相關。圖1(a)～(c)分別表示Na隨3個參數的變化情況，可以發現，壓力的影響最大，當壓力從0.101 MPa增大到19.8 MPa時，Na的數量級從100增大到106。而Na隨接觸角僅呈緩慢的增長，其中接觸角包含壁面潤濕度和粗糙度的影響，因此可以認為相比壁面過熱度和壓力，材料的影響相對較弱。

相較之下，液體過冷度和質量流速的影響還沒有一個統一的結論。Basu等[3]認為液體過冷度和質量流速均無法獨立影響Na，兩者的影響被壁面過熱度和熱流密度的影響包含在內。Zhou等[12]同樣認為相較壁面過熱度和壓力，液體過冷度和質量流速的影響可以忽略。相反，Ai等[5]認為，當質量流速增加時，壁面的熱邊界層厚度減小，進而Na變少。Ren等[4]則認為Na隨液體過冷度和質量流速的增加而減小，因為兩者會抑制汽泡的核化。本文根據流動沸騰實驗結果，對比分析液體過冷度和質量流速對活化核心密度的影響,其中質量流速的影響采用雷諾數Re：

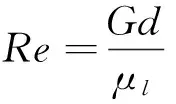
(2)

式中：G為質量流速；d為管道水力直徑；μl為液體動力粘度。

對于過冷流動沸騰，由于汽泡尺寸通常大于過熱液層厚度，因此汽泡的生長同時受壁面的蒸發作用和主流的冷凝作用，當蒸發作用和冷凝作用相等時，汽泡脫離或浮升[18]。而對于汽泡在壁面的核化，圖1(d)表示液體過冷度的影響，此時由于汽泡尺寸還非常小，受壁面的蒸發作用影響更明顯，因此相比壁面過熱度，主流過冷度的影響基本可以忽略。圖1(e)表示雷諾數的影響，雖然雷諾數越大，過熱液層的厚度越小，但此時沸騰換熱更加劇烈，換熱效率更高，因此，整體而言，Na并不隨雷諾數呈現明顯變化。

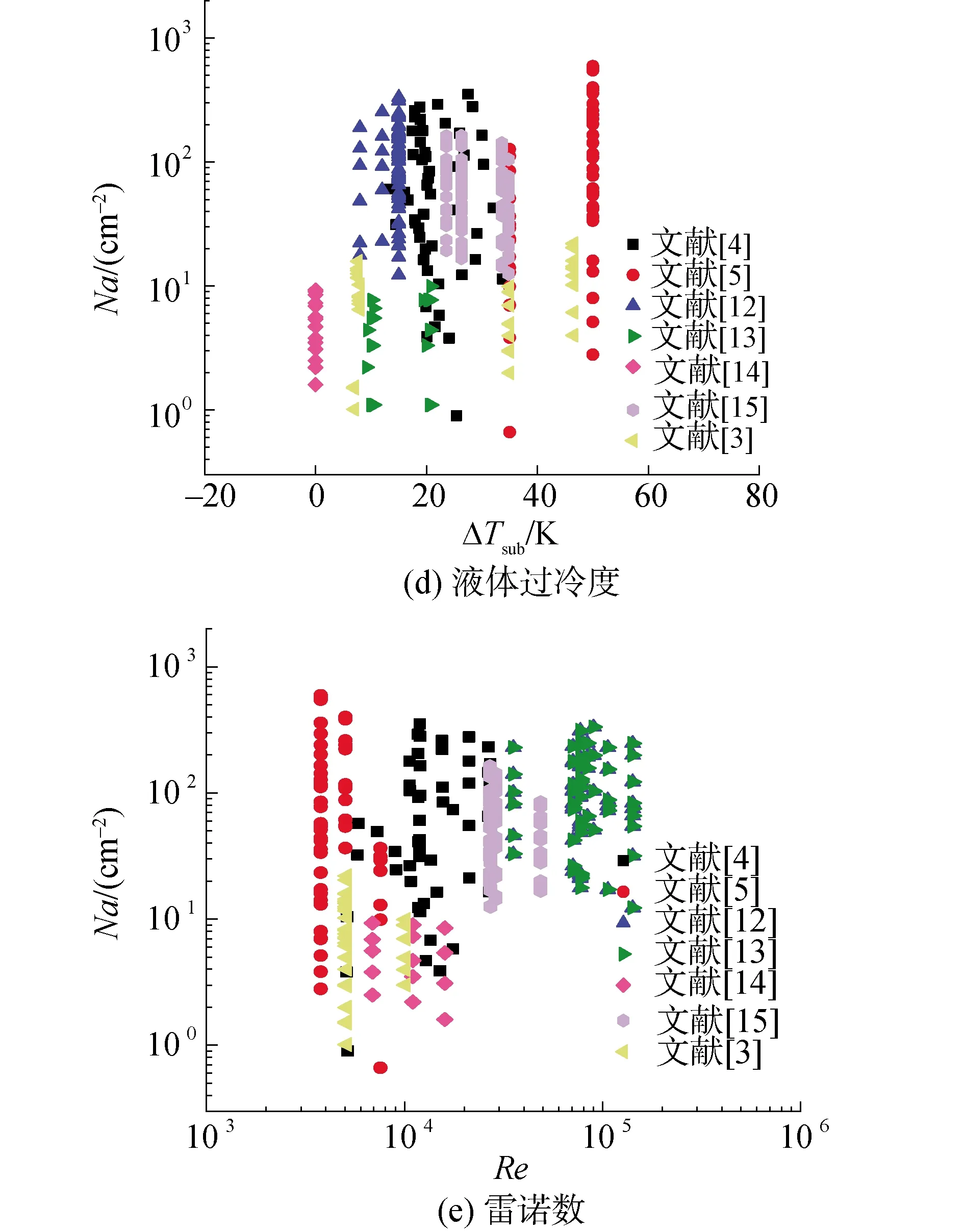
圖1 活化核心密度受各參數影響情況Fig.1 The effects of parameters on nucleation site density

綜上，活化核心密度隨壁面過熱度、接觸角和壓力的增大而增大，其中壓力的影響最大，接觸角的影響最小，而即使在流動沸騰下，液體過冷度和雷諾數的影響也基本可以忽略。

2 預測模型適用性評價

雖然液體過冷度和雷諾數對活化核心密度的影響很小，但是池沸騰和流動沸騰依然存在較大區別，因此，本文選擇5組活化核心密度預測模型，分別為文獻[2]模型、文獻[3]模型、文獻[4]模型、文獻[5]模型和文獻[19]模型，分別按照流動沸騰和池沸騰進行適用性評價，其中文獻[4，5]模型僅適用于流動沸騰。評價指標采用絕對誤差eA、相對誤差eR和相對誤差處于±50%誤差線內的數據比例N50，具體表達式為：

(3)

(4)

式中：Na,cal為活化核心密度通過預測模型得到的計算值；Na,exp活化核心密度的實驗值。

對于池沸騰，從表1可見，文獻[3]模型準確度均較低，絕對誤差分別為61.4%和69.5%，前者誤差較大的原因在于其僅考慮了壁面過熱度和接觸角的影響，因此應用到壓力范圍較大的實驗(0.101～19.8 MPa)時，預測值遠遠低于實驗值[16]。文獻[3]模型雖然采用汽液密度比反映壓力的影響，當壓力小于7 MPa時準確度較高，但當壓力繼續增大后，誤差明顯增大，具體如圖2所示，反映了預測值處于±50%誤差內的情況。考慮到壓力影響較大，文獻[9]模型則在文獻[2]模型的基礎上直接采用壓力替代密度比，擬合Na隨壓力的變化情況，得到的新模型準確度最高，整體誤差為32.3%，能應用于大壓力范圍內池沸騰活化核心密度的預測中。

表1 現有預測模型準確度Table 1 Predicting accuracy of current predicting models

對于流動沸騰，可以發現文獻[4，5]模型的準確度最低，前者雖然絕對誤差只有88.1%，但是從圖2可以明顯看到，低估了實驗值，只能預測10.2%的數據在±50%的誤差線內。經分析，2個模型誤差大的原因在于兩者均根據自身開展的實驗數據擬合而來，實驗僅采用一種材料，因此兩者均忽略了材料對活化核心密度的影響，并且文獻[4]模型應用于工質為R113的文獻[14]數據時誤差高達35 974%，可見該模型很難應用于水以外的工質。文獻[3，19]模型的誤差依然較大，兩者絕對誤差分別為142.4%和176.1%。相較之下，文獻[2]模型能將最多的實驗數據預測至±50%誤差線(47.8%)，但整體絕對誤差依然較大(106.1%)，從相對誤差來看，原因在于其高估了流動沸騰下的活化核心密度，未來可對其進行修正進而降低誤差。

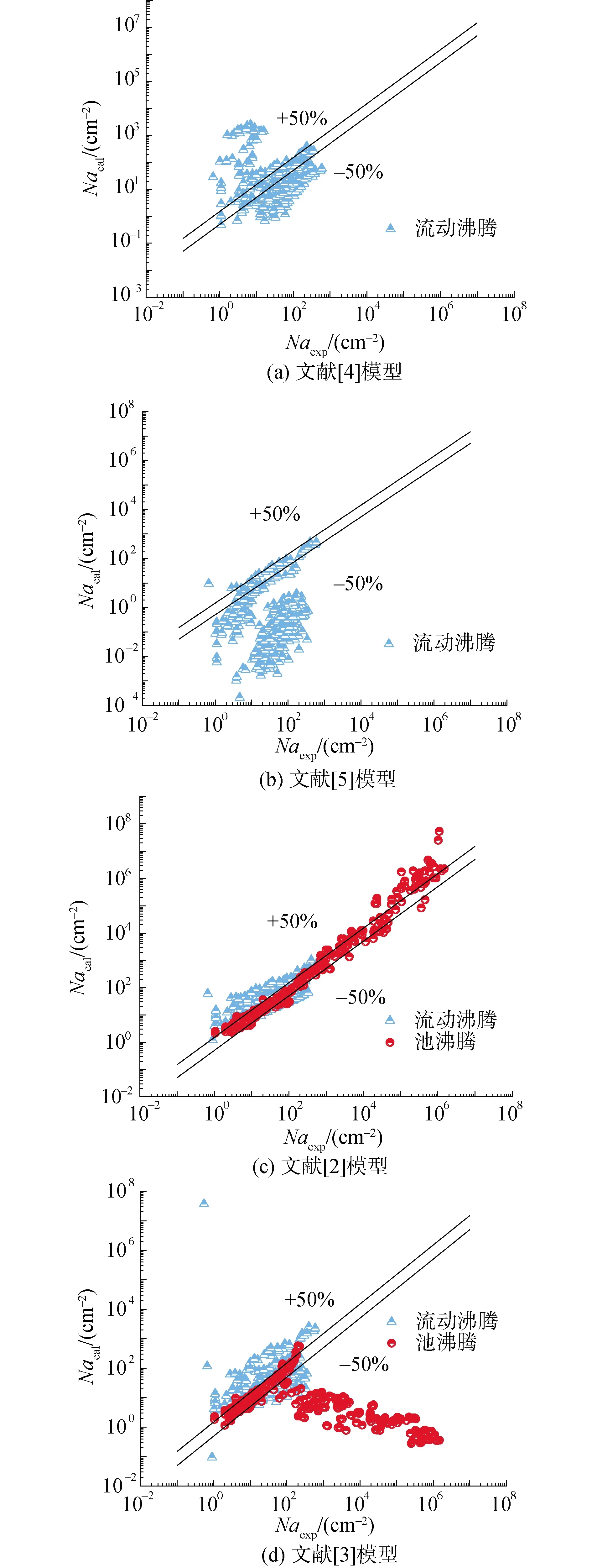
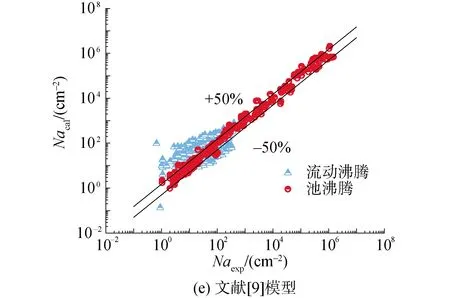
圖2 各預測模型準確度對比Fig.2 Accuracy comparison of current empirical correlations

3 活化核心密度隨機性分析

活化核心密度預測模型在流動沸騰下的準確度均較低，原因在于流動沸騰換熱更加復雜，此時壁面過熱度等參數受渦流等的影響呈現隨機分布，進而造成活化核心密度在同一工況下也可能呈現隨機分布，采用一個定值來預測準確度不高。

目前關于活化核心密度在成核表面的空間分布已有較為成熟的研究，普遍采用泊松分布描述，但是由于沸騰本身引起的概率分布研究還非常少。本文利用有限的實驗數據，參考汽泡脫離直徑的研究[10-11]，確定活化核心密度是否呈現隨機分布，并采用常用的正態分布、對數正態分布和伽馬分布，比較三者用于描述該分布時的準確性。由于目前尚未發現有文獻對同一工況下的活化核心密度進行重復實驗(通常需要200次以上[10])，因此選擇3組數據點較多或工況相近的數據，其中包括流動沸騰所有412個數據[3-5，12-15]、具有相同實驗材料的126個數據[5，18]、以及169個數據。圖3呈現的概率密度函數表示不同活化核心密度數值范圍內的汽泡數占總汽泡數的比例呈現的函數分布，可以發現，3組數據均呈現明顯的隨機分布。圖3(a)和(b)對比發現，由于Na值明顯集中在較小數值內，正態分布和伽馬分布誤差均較大，對數正態函數準確度更高。而對于文獻[15]數據，圖3(c)顯示3個分布函數差異不大，但是由于正態分布存在將數值預測為負值的情況，依然認為對數正態分布函數更適合于描述流動沸騰下汽泡成核的分布。

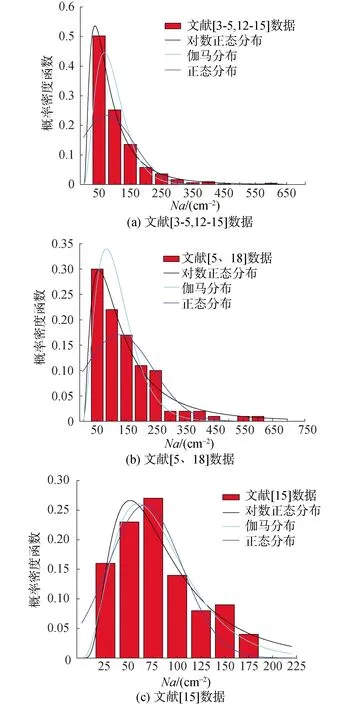
圖3 流動沸騰概率密度函數準確度對比Fig.3 Accuracy comparison of probability density functions in flow boiling

4 結論

1)經對比分析，活化核心密度隨壁面過熱度、接觸角和壓力的增大而增大，其中壓力的影響最大，接觸角的影響最小，而即使在流動沸騰下，液體過冷度和雷諾數的影響也基本可以忽略。

2)對比5個現有預測模型，發現池沸騰下文獻[9]模型準確度最高，但流動沸騰下這些模型的誤差均較大。

3)目前，活化核心密度在成核表面的空間分布研究較多，該分布主要由材料的不均勻性引起，但由于沸騰本身的不穩定性引起的隨機分布，目前的研究還基本沒有。本文利用現有實驗數據，經對比發現活化核心密度在流動沸騰下呈現對數正態分布。

由于數據缺乏，本文難以直接擬合概率分布模型，但為將來開展實驗，以及提高活化核心密度的預測準確度和在工程中提高沸騰換熱計算的準確度提供了研究思路和理論基礎。