軌道非線性能量阱尖端效應分析及簡化設計方法研究

張 超，鄭雨強，王菁菁

（1.湖南工業大學 土木工程學院，湖南 株洲 412007；2.中國建筑第四工程局有限公司，廣東 廣州 510000；3.廣州大學 土木工程學院，廣東 廣州 510006）

1 研究背景

結構控制技術通過對主體結構施加被動或主動的作用力，改變主體結構的剛度或阻尼以有效減小結構振動[1]。其中，調諧質量阻尼器（tuned mass damping，TMD）是工程結構中應用最為廣泛的被動控制方法，一般被放置在主體結構頂層，當TMD 與主體結構相調諧時兩者形成共振機制，從而減小主體結構響應[2-3]。但當主體結構受到損傷、沉降或其他因素影響時，結構自振頻率發生變化，TMD 與之失諧而導致減振性能退化，甚至會增大結構響應[4]。

為了解決TMD 對結構變化頻率敏感的問題，有學者提出非線性的結構控制方法——非線性能量阱（nonlinear energy sink，NES）[5]。 國 外 學 者S.Aubry[6]、G.Kopidakis[7]等的研究表明，與TMD 相比，NES 的非線性力-位移使其能夠在寬頻范圍內發生共振，降低結構響應，其頻率魯棒性能優于TMD。此外，國內學者也對NES 進行了相關的研究，如張也弛等[8]使用數值方法研究了兩自由度NES 在簡諧荷載下的力學特性和振動控制效果。王菁菁等[9-11]提出了一類新型被動質量阻尼器——軌道非線性能量阱，該裝置由軌道和附加質量塊組成，如圖1 所示。通過軌道形狀實現非線性恢復力，軌道固定在主體結構頂層，質量塊沿軌道運動，如圖2 所示。Wang J.J.等[12]研究了兩自由度主體結構附加軌道NES 在脈沖荷載作用下的減振性能，實現了具有近似3 次方恢復力的軌道NES。同時，研究發現軌道NES 的力-位移關系中產生尖端效應，這是軌道NES 特有的現象，未見于其他類型的NES。尖端效應是指當NES 質量塊位移較大、軌道斜率極大時，恢復力隨著位移的增大反而減小。當無尖端效應發生時，軌道NES 的減振效率難以達到最佳；當存在一定程度的尖端效應時，軌道NES 的減振效率較好。尖端效應可以防止軌道NES 恢復力過大而造成局部構件發生破壞。

本研究對軌道NES 尖端效應進行理論推導，得到了軌道NES 尖端效應產生的主要原因，并分析了尖端效應的強烈程度。分別通過不同輸入能量下的無阻尼軌道NES 的自由振動、有阻尼軌道NES 的受迫振動，對軌道NES 的尖端效應進行分析。根據所得到的分析結果，揭示了軌道NES 尖端效應產生的主要原因，從而提出了基于尖端效應的軌道NES 簡化設計方法。

圖1 軌道NES 示意圖Fig.1 configuration of track NES

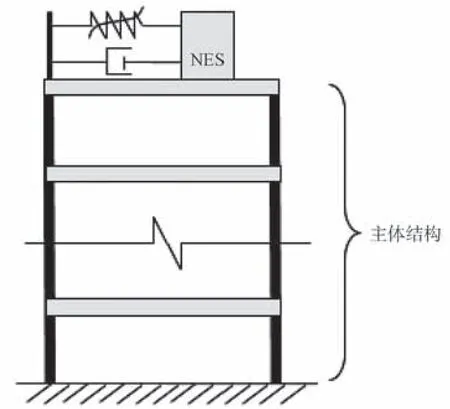
圖2 軌道NES 系統示意圖Fig.2 Illustration of track NES system

2 軌道NES 恢復力

軌道NES 的自由體受力示意圖如圖3 所示，其中，mN為NES 的質量，g為重力加速度，θ為軌道切線角度，FNormal為NES 作用在軌道上的法向力，uN和vN分別為NES 相對于軌道的水平位移和豎向位移，z為軌道的水平位移，h(uN)為軌道的形狀函數，即NES 的豎向位移。

圖3 軌道NES 自由體的受力示意圖Fig.3 Force diagram of track NES

推導中假設NES 質量不發生轉動且始終與軌道接觸，采用牛頓方法可以得到軌道NES 的運動方程。根據圖3 列出水平方向上的力平衡方程為

豎直方向上的力平衡方程為

將式（3）和式（4）代入力平衡方程式（1）和式（2），并聯立式（5）可得：

3 軌道NES 尖端效應理論推導

本節對軌道NES 尖端效應進行理論推導，得出了軌道NES 尖端效應的產生原因，分析了尖端效應的強烈程度。

在恢復力表達式（8）中，第一項和第二項分別與軌道NES 的加速度和速度有關，同時也與位移的高階項有關，而第三項僅與位移相關。為了簡便起見，將這3 項分別記為Fa、Fv和Fd，可得它們之間的關系如下：

式中：

采用諧波平衡法進行分析，相關研究[13]中，當且僅當取一階頻率進行近似求解時所得結果與數值模擬結果吻合良好，因此，本文取一階頻率項進行分析。無阻尼軌道NES 的自由振動可以寫成：

式（13）～（16）中：A為振動的振幅；ωN為根據式（16）定義的軌道NES 的瞬態自然頻率；φN為振動的初相。

因此，恢復力可寫成

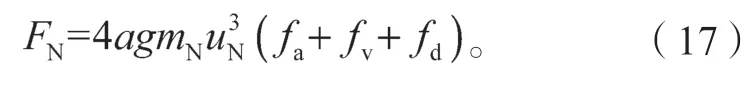
式中：

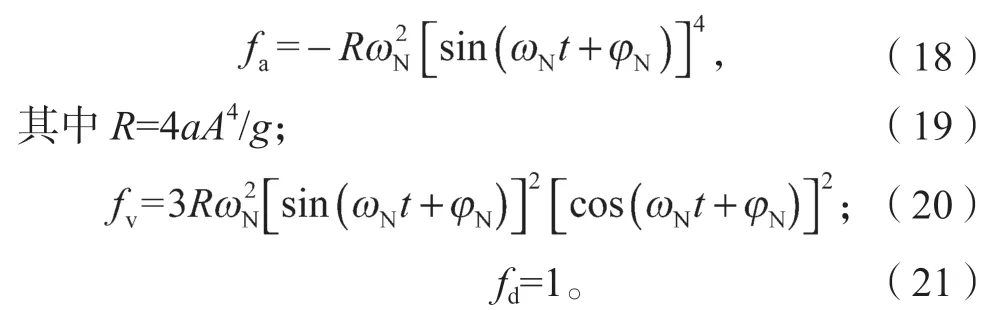
由于fd等于1，fa和fv表示Fa和Fv相對于Fd的作用力方向和大小比例。

分析式（18）～（21），可以得出：

1）由于R始終為正，因此fa為負，fv為正，這說明Fa始終與Fd方向相反，Fv始終與Fd方向相同。

2）R是與軌道NES 參數有關的常數。因此，當ωN非常小時，Fa和Fv的量級遠小于Fd，可以在FN中忽略。此時FN≈Fd，且軌道NES 的瞬態自然頻率變成

令

ra和rv是關于ωN的單變量函數，其函數圖像如圖4所示，可用于分析軌道NES尖端效應的強烈程度。

根據圖4 所示曲線圖可以得知：當φN=0 時（即對應初始位移為0，僅具有初始速度的自由振動）ra和rv隨著ωN而變化。

圖4 ra 函數和rv 函數Fig.4 ra and rv as functions of ωN

根據觀察可以推導得到有關軌道NES 恢復力的一些特點：

1）在rv曲線中，觀察到其絕對值首次減小發生在ωN=1 rad/s，其頻率低于ra絕對值首次減小時所對應的頻率，ra和rv絕對值的減小表明了其對應分力Fa和Fv的減小。

2）軌道NES 的剛度隨位移增大而增大，因此分力Fv減小所對應的位移小于分力Fa減小所對應的位移，表明Fv絕對值的減小早于Fa絕對值的減小，當各分力的減小程度不同步時會導致合力FN的大小發生上下波動，即產生尖端效應。

3）ra和rv的變化隨著頻率的增加而變得更加劇烈，表明在更大的位移處尖端效應更加顯著。

4）隨著Fv首次減小，FN中觀察到尖端效應，而尖端效應發生后，隨著位移的增加，ωN不增大反而減小，這使得Fa的減小太可能發生。

為了直觀地說明軌道NES 的尖端效應，下面討論無阻尼軌道NES 的自由振動和有阻尼軌道NES 的受迫振動，軌道形狀均采用h(uN)=0.015uN4。

4 無阻尼軌道NES 尖端效應分析

圖5 為NES 質量塊的初始速度為0.42 m/s 時，無阻尼軌道NES 的加速度、速度和位移時程曲線圖。

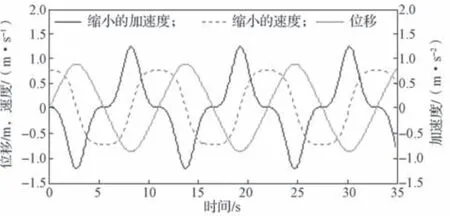
圖5 0.42 m/s 初始速度下無阻尼軌道NES 的響應曲線Fig.5 Responses curve of undamped track NES at an initial velocity of 0.42 m/s

可以很明顯地從圖5 中得知振動頻率，ωN,a=0.57 rad/s。同時，為了在同一張圖中顯示3 個運動變量的時程曲線，速度和加速度分別按進行縮小，縮小后的曲線如圖5 所示。

圖6 為圖5 中的運動產生的恢復力FN及其分力Fa、Fv和Fd隨位移變化的曲線圖。從圖6a 可以看出，Fa始終與Fd方向相反，Fv始終與Fd方向相同，這與第3 節中得出的結論相同。

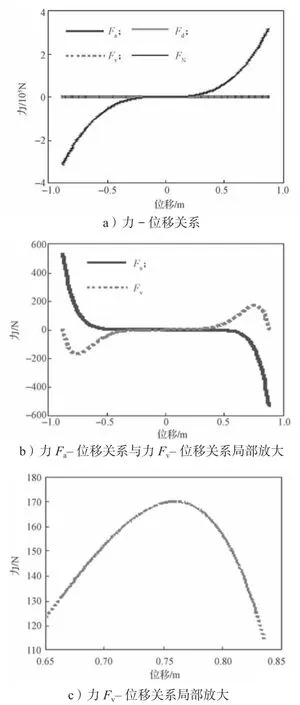
圖6 0.42 m/s 初始速度下無阻尼軌道NES 的力-位移關系曲線Fig.6 Force-displacement relationship curve of undamped track NES at an initial velocity of 0.42 m/s

此外，在所示運動的能量等級，Fa和Fv非常小并且與Fd相比可以忽略。fa和fv的大小可以將ωN,a=0.57 rad/s 代入進行計算，如式（26）和（27），均遠小于fd=1。因此，式（22）可用于計算Fv在如式（28）所示的絕對值（ωN=1）處首次減小時，軌道NES 的位移，與圖6c 所示的Fv峰值時的位移（約為0.75 m）相一致。然而，Fv的這種減小不會在FN中產生有效的尖端效應，因為此時負向分力Fa增加的速率遠快于Fv，并且Fa和Fv都遠小于Fd，不能使FN發生顯著的變化。

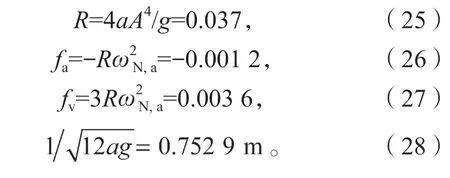
圖7 和圖8 分別描述了當自由體獲得5 m/s 初始速度（輸入能量相對較高）的無阻尼軌道NES 的運動狀態時程曲線圖和恢復力-位移關系曲線。圖7 中，速度和加速度時程分別按1/ωN,a（ωN,a=1.53 rad/s）和進行縮小。在這種情況下，圖8 中，Fa和Fv與Fd具有相同的數量級。在Fv中可以很清晰地觀察到力隨位移先增大后減小的變化，在位移的終端可以識別出在Fa中發生了微弱的尖端趨勢，在FN中尖端效應顯著。此時，由于FN與Fd已不再相同，式（22）不能在此處用于計算Fv達到峰值時的位移。

圖7 5 m/s 初始速度下無阻尼軌道NES 的響應曲線Fig.7 Responses curve of undamped track NES at an initial velocity of 5 m/s

圖8 5 m/s 初始速度下無阻尼軌道NES 的力-位移關系曲線Fig.8 Force-displacement relationship curve of undamped track NES at an initial velocity of 5 m/s

5 有阻尼軌道NES 尖端效應分析

圖9 和10 分別是阻尼系數為1.7×105N·m/s 時，有阻尼軌道NES 附加在文獻[14]中的32 自由度，主體結構頂層時的運動狀態時程曲線圖和恢復力-位移關系曲線圖。主體結構每層以及NES 質量塊的初始速度都為1 m/s。圖9 中軌道NES 的運動以主體結構頂層運動為參考，即為兩者的相對運動，并且速度和加速度時程曲線分別按1/ωN,a（ωN,a=1.58 rad/s）和進行縮小。由于軌道NES 中阻尼的存在以及主體結構運動的激勵，軌道NES 的特性變得更加難以推測。Fv和Fa絕對值的減小每次都發生在不同的位移處，并且在尖端效應發生的位移范圍內有小幅度波動。此示例定性地論證了圖4 中的推論：Fv的減小比Fa的減小更容易發生，Fv是軌道NES 中產生尖端效應的主要原因，并且在較大的位移處尖端效應更加顯著。

圖9 基激勵下有阻尼軌道NES 的響應曲線Fig.9 Responses curve of damped track NES under base excitation

圖10 基激勵下有阻尼軌道NES 的力-位移關系曲線Fig.10 Force-displacement relationship curve of damped track NES under base excitation

6 結論

尖端效應是軌道非線性能量阱的力-位移關系中存在的特有現象。本研究進行了尖端效應理論推導，分析了不同情況下軌道NES 的尖端效應，得出以下結論：

1）分力Fv減小所對應的位移小于分力Fa減小所對應的位移，表明Fv絕對值的減小早于Fa絕對值的減小，各分力的減小程度不同步導致合力FN的大小發生上下波動，即產生尖端效應。

2）無阻尼軌道NES 尖端效應分析結果表明，輸入能量相對較低時，分力Fa和Fv非常小且與Fd相比均可以忽略。由于負向分力Fa增加的速率遠快于Fv，且Fa和Fv都遠小于Fd，不能使FN發生顯著的變化，Fv的減小不會在FN中產生有效的尖端效應。輸入能量相對較高時，在Fv中可以很清晰地觀察到力隨著位移先增大后減小的變化，在位移終端可以識別到在Fa中發生了微弱的尖端趨勢，且在FN中尖端效應顯著。

3）有阻尼軌道NES 尖端效應分析結果表明，Fv和Fa絕對值的減小每次都發生在不同的位移且在尖端效應發生的位移范圍內有小幅度波動，可以定性地說明Fv的減小比Fa的減小更容易發生，Fv是軌道NES 中產生尖端效應的主要原因，在較大的位移處尖端效應更強。

基于上述結論：在Fv達到峰值以前，Fv和Fa的絕對值大小相近，且由于Fa和Fv的方向總是相反，Fd成為FN中最具有代表性的項，可采用Fd（式（12））作為其恢復力進行軌道NES 的初步設計。