基于組稀疏殘差去噪的磁共振圖像重構

（浙江理工大學 信息學院，浙江 杭州 310018）

0 引言

磁共振成像（Magnetic Resonance Imaging，MRI）是一種對人體無輻射傷害的診斷方法，具有多方位、多參數、多模態等優點，能夠提供豐富的診斷信息［1］，這些優點使得MRI成為醫學研究的重點領域之一。然而，成像時間長是其不可避免的缺點，如何重構高質量的磁共振圖像以便醫護人員更好地對病灶進行診斷是研究的重點。壓縮感知［2］（Compressed Sensing，CS）打破了傳統的奈奎斯特采樣定理，使得僅采集少量數據就能恢復出高質量的信號成為可能。基于壓縮感知的磁共振成像［3］（CS-MRI）是MRI 的一個重大突破，利用CS 原理，不僅磁共振數據采集量大大減少，而且圖像重構質量也相應提高。

全變差分［4］（Total Variation，TV）能夠有效地保留圖像邊緣信息，是一種經典的圖像稀疏方法。2016 年，馬杰等［5］提出一種基于全變分正則化低秩稀疏分解的動態MRI重建方法，通過在低秩加稀疏分解模型基礎上，結合TV 正則化項，最終使用非精確增廣拉格朗日算法對模型求解。該算法在重構精度及速度上都有較大提高。Varghees 等［6］提出一種基于TV 最小化模型和本地噪聲估計技術以自適應地去除圖像中的噪聲，實驗表明，該方法既能保留原始圖像的邊緣信息，又可成功減少Ricaian 噪聲。非局部均值［7］（Non-Local Means，NLM）去噪的基本思想是當前像素的估計值由圖像中與它具有相似領域結構的像素加權平均得到，能夠最大程度地保持圖像的細節特征。2015 年，陳創泉［8］對一些改進的NLM 方法加以總結，實現MRI 圖像去噪，分析利用NLM 技術進行磁共振圖像去噪的關鍵技術以供研究人員參考。BM3D（Block Matching of 3D Fil?tering，BM3D）是一種基于NLM 和稀疏表示的性能優越的圖像去噪算法［9］，該方法通過相似性準則找到與參考塊相似的二維圖像塊，按照相似度大小堆疊成三維相似組，將其變換到三維空間域后進行協同濾波處理，將最終得到的近似圖像塊進行加權平均后返回到原始圖像塊位置以得到最終恢復圖像。

BM3D 是公認的去噪性能優越的算法，基于BM3D 的磁共振圖像重構算法陸續被提出。Eksioglu 等［10］將BM3D算法作為基于噪聲去除的迭代閾值算法（Denoising-based Iterative Thresholding，D-IT）和去噪近似消息傳遞算法（DAMP）的去噪先驗進行磁共振圖像重構［11］。前者的主要思想是將迭代閾值算法中的閾值處理看成是噪聲去除操作，從而使用BM3D 算法實現噪聲去除，這種方法簡稱為BM3D-IT-MRI；后者的主要思想是利用現有噪聲去除算法實現去噪近似消息傳遞算法中的濾波操作。由于磁共振圖像的數據具有復值特性，Eksioglu 等［10］將數據分為實和虛兩個通道分別加以處理，采用BM3D 算法去除噪聲，這種方法簡稱為BM3D-AMP-MRI。2015 年，Qu 等［12］提出一種基于塊的非局部算子（Patch-based Nonlocal Operator，PANO），該算法通過PANO 算子盡可能地對相似塊組進行稀疏化，最終實現磁共振圖像重構；2017 年，Zha 等［13］提出組稀疏殘差約束的圖像去噪算法，該算法將圖像去噪問題轉化成最小化組稀疏殘差問題，首先將BM3D 算法應用于噪聲圖像，再對降噪后的圖像使用組稀疏殘差法估計出組稀疏集合，相應地得到估計圖像。這種算法是在BM3D 去噪基礎上實現組稀疏系數最小化，實驗表明，該算法去噪性能優于BM3D 算法。

BM3D-AMP-MRI 是近年來提出的一種重構性能較高的重建算法，其主要思想是將BM3D 作為去噪近似消息傳遞算法的去噪先驗。由于GSRC 是一種去噪性能較BM3D優越的去噪算法，為獲得更高的磁共振圖像重建精度，本文將GSRC 作為去噪近似消息傳遞的去噪先驗。將DAMP 迭代重構的圖像估計值和噪聲標準差作為GSRC 算法的初始噪聲圖像和噪聲標準差，經GSRC 去噪后得到的圖像以進一步實現D-AMP 算法的殘差更新。最終實驗結果表明，基于GSRC 的磁共振圖像重建算法不僅有效保留了原始圖像的細節信息，而且提高了重建質量，并具有較強的魯棒性。

1 基于組稀疏殘差的磁共振圖像重構方法

傳統的磁共振圖像重構模型如式（1）所示。

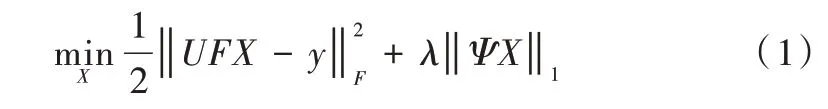
其中，X為待重構的MR 圖像，F是傅里葉操作算子，U為欠采樣矩陣，y是測量的K 空間數據，Ψ代表稀疏變換。式（1）中前半部分表示數據的保真項，后半部分λ‖ΨX‖1代表數據的懲罰項或者稀疏項目，參數λ用來平衡數據的保真項和稀疏項，使得求解出的X更加接近原始圖像。

1.1 組稀疏系數殘差去噪

組稀疏模型表示如式（2）所示。

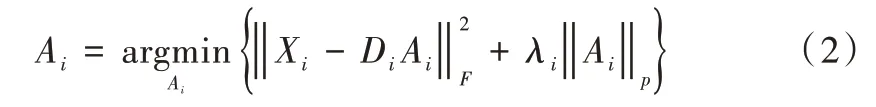
組稀疏基本思想如下：X∈RN是一幅清晰的圖像，將X分割成m個尺寸固定的圖像塊，將這m個重疊的圖像塊表示為xi,i=1,2,...,m。在固定的窗口中（大小為W×W）尋找n個相似塊，這些相似塊組表示為Xi，定義為Xi={xi,1,xi,2,...,xi,n}。xi,n表示第i組中第n個相似塊，Ai表示相似塊組Xi的組稀疏系數。Di表示稀疏字典，本文使用的是PCA 子字典，使得。‖·‖F表示Frobenius 范數，‖Ai‖p為模型的稀疏項，‖·‖p表示lp范數，p的取值為0 或者1，λi是正則化參數。式（2）表明整個圖像能夠通過組稀疏編碼的集合{Ai}進行表示。

對于磁共振成像而言，式（1）中原始圖像X未知，其研究目的在于重構出與X近似的。本文基本思想是使用迭代磁共振重構算法，每次迭代都會得到一個與原始磁共振圖像近似的含有噪聲的圖像，假設為R，從R中提取n個噪聲圖像塊ri,i=1,2,...m，找到噪聲圖像塊ri的相似塊，并組成相似塊組Ri={ri,1,ri,2,...,ri,n}。此時磁共振圖像去噪轉化為利用組稀疏編碼從Ri中恢復Xi。

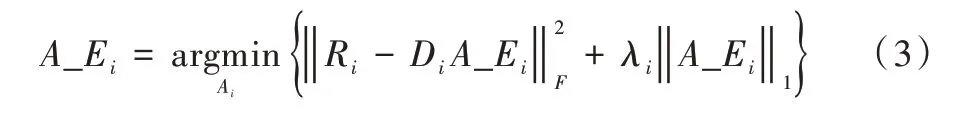
當獲得所有組稀疏系數{A_Ei}，通過Xi重建原始磁共振圖像X。

對比式（2）和式（3），將求解問題轉化為縮小估計的組稀疏系數A_E與原始圖像的組稀疏系數A之間的誤差。因此，可以將問題轉化為通過定義殘差進行相應的求解計算，即組稀疏系數A_E與組稀疏系數A的差值，用Red表示，如式（4）所示。最終將求解問題轉換為如何減小組稀疏系數殘差Red問題，其模型表示如式（5）所示。

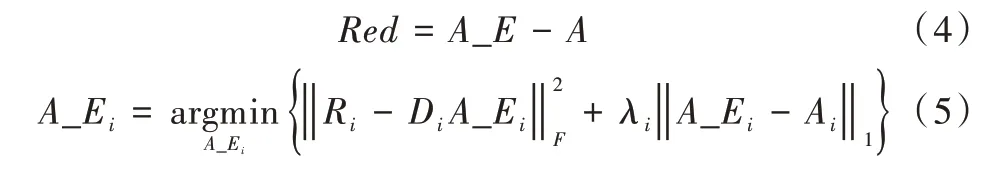
真實的組稀疏編碼A是未知的，本文首先對迭代過程中噪聲圖像R使用BM3D 方法去噪，將去噪后的結果表示為Z，用Z的組稀疏系數取代未知A。因此式（5）中，只有A_Ei是待求解的變量。

文獻［13］證明式（5）在第t+1 次迭代中，計算方式如式（6）所示。

其中，Sλ(?)是軟閾值操作算子，表示第i次重構相似塊組。相似塊組Redi對應參數λi設置如式（7）所示。

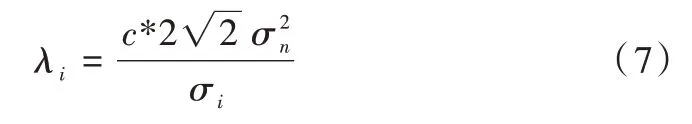
其中，σi表示Red的估計方差，c 是一個非常小的常量。在第t+1 次迭代過程中，噪聲標準差計算如式（8）所示。

其中，γ表示一個小常數。當求出A_Ei后，重構的圖像塊組，最終通過聚合所有圖像塊組得到去噪后的圖像。

1.2 磁共振圖像重構

D-AMP 算法是一種基于噪聲去除的算法，本文使用該算法對磁共振圖像進行重構，并將GSRC 去噪算法作為該重構算法的先驗知識。最終結果表明，該方法能夠重構出質量相對較高的圖像。基于組稀疏殘差去噪的近似消息傳遞磁共振圖像重構流程如下：①輸入零填充的磁共振圖像X0=（FΩ表示欠采樣傅里葉算子），迭代殘差z0=y；②計算初步得到的估計值；③計算噪聲標準差，N為y的長度；④使用GSRC 算法對Riter去噪，；⑤計算Onsager校正項；⑥更新殘差ziter=y-FΩ Xiter+qiter；⑦判斷迭代次數是否達到最大次數，滿足則輸出最終重構值，否則返回步驟②。

1.3 實驗方法

本文使用的實驗數據如圖1（a）—圖1（c）所示，實驗使用3 組數據比較幾種重建算法的重建表現。這3 組數據分別是人的腦部［14］（Brain）、心臟［15］（Heart）及上半身圖［14］（Bust）。其中，Heart 的數據來源于文獻［14］中三維心臟的第十幀數據。采樣模式不同會影響圖像重構質量，本次實驗將選用偽徑向［16］和笛卡爾采樣兩種模式對原始磁共振數據進行欠采樣，圖1（d）和圖1（e）展示了采樣率為20%的偽徑向采樣和30% 的笛卡爾采樣mask。為了驗證算法的有效性和準確性，本文算法均運行在Matalab R2016a 軟件上，主機CPU 的配置為Intel Core i5，內存為8G，操作系統為Windows 10。

對比算法有基于BM3D 去噪的迭代閾值磁共振圖像重構算法［10］（BM3D-IT-MRI）、基于塊的非局部算子PA?NO［12］以及基于BM3D 的近似消息傳遞算法［10］（BM3DAMP-MRI）算法。為了衡量重構效果和算法性能，本實驗計算峰值信噪比（Peak to Signal Ratio，PSNR）和相對L2范數誤差（RelativeL2Norm Error，RLNE）。PSNR 是一種常用的評價圖像重構質量好壞的指標，PSNR 值越高表明圖像重構性能越好。RLNE 用來表示重構圖像與原始圖像的偏差，RLNE 值越小，表明重構圖像越接近原始圖像。除使用PSNR 和RLNE 兩個指標外，將會對重構圖像的細節進行放大分析，觀察不同重構算法保留原始圖像細節能力上的差異。

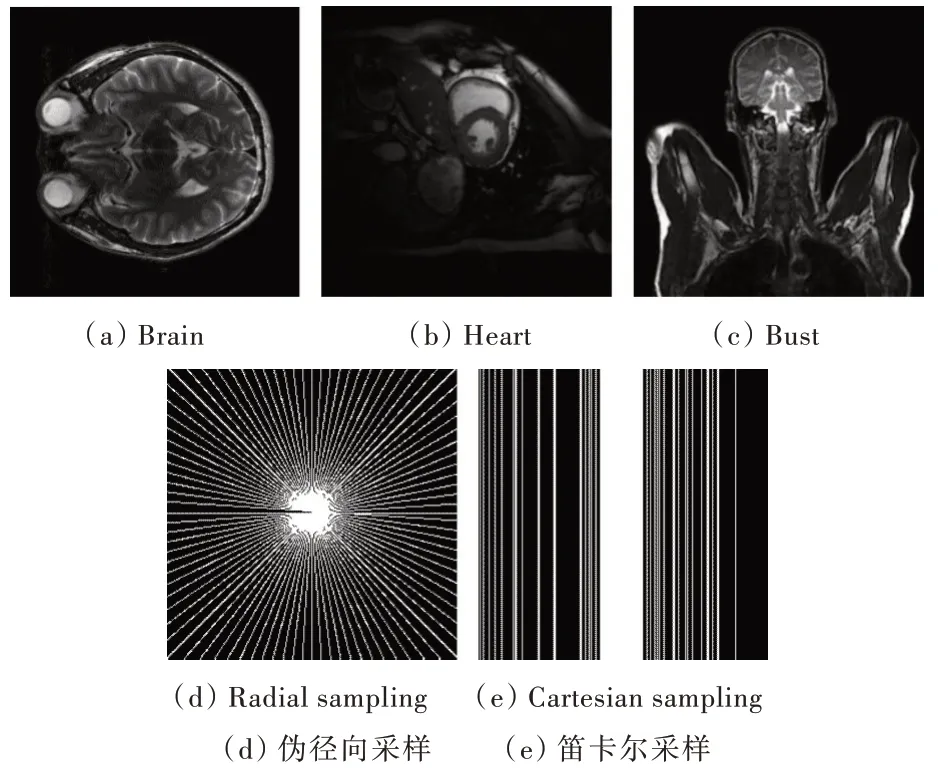
Fig.1 Experimental source data and two sampling masks圖1 實驗源數據以及兩種采樣mask

2 實驗結果與分析

表1、表2 展示了在采樣率為20% 和30% 的條件下，磁共振圖像重構的PSNR 和RLNE 值。其中，加粗數據表示相同條件下得到的最高PSNR 和最低的RLNE 值。根據表1 計算得出，在20% 采樣率下，本文算法重構的PSNR值較BM3D-IT-MRI、PANO 及BM3D-AMP-MRI 算法平均增加3.8dB、1.3dB 和1dB，RLNE 平均降低0.060 7、0.016 5、0.017 7。因此，可以判定本文重構性能高于其它3 種算法。對比發現，相同采樣率下，偽徑向采樣模式下重構圖像的PSNR 均高于笛卡爾采樣模式下的PSNR 值、RLNE值均低于笛卡爾采樣模式下的RLNE 值，可知偽徑向采樣是一種優于笛卡爾采樣的模式。比較表1 和表2 可知，對于同一源數據，相同采樣模式下，20% 欠采樣的圖像重構質量比30% 欠采樣重構的圖像質量差，說明采樣率越高，獲取到源數據的有用信息越多，最終重構質量也越高。

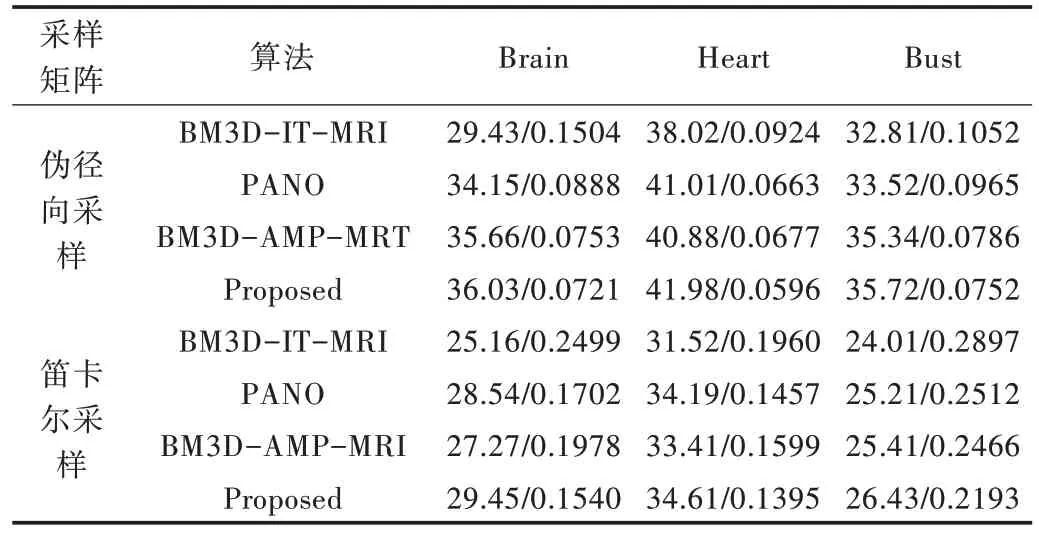
Table 1 The PSNR/RLNE of reconstructed image under 20% under-sampling表1 20% 欠采樣條件下圖像重構的PSNR/RLNE

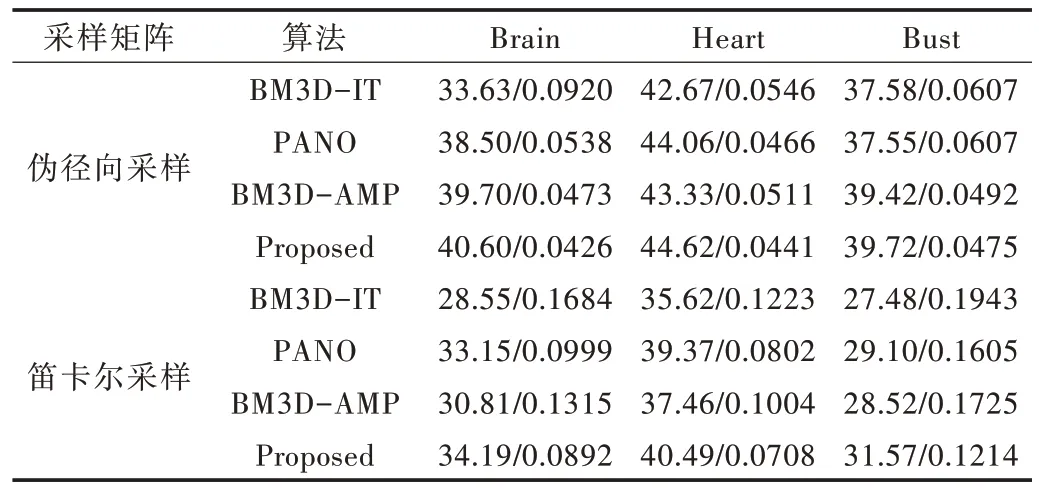
Table 2 The PSNR/RLNE of reconstructed image under 30% under-sampling表2 30% 欠采樣條件下圖像重構的PSNR/RLNE

20% 偽徑向采樣模式下，Bust 圖像的重構細節放大圖及放大10 倍后的重構誤差如圖2 所示（彩圖掃OSID 碼可見），第一行從左到右分別為原圖、BM3D-IT-MRI 重構細節圖、PANO 重構細節圖、BM3D-AMP-MRI 重構細節圖以及本文算法的重構細節圖；第二行從左到右分別為20% 偽徑向采樣mask、BM3D-IT-MRI 重構誤差圖、PANO 重構誤差圖、BM3D-AMP-MRI 重構誤差圖以及本文算法重構誤差圖。圖2 的第一行內容中，較小的紅色框內表示待放大重構區域，較大的紅色框內表示經放大后的待觀察重構區域，對比發現，本文算法對原始細節信息保留得更好，更加接近原始圖像。并且，由圖2 的第二行可以看出，本文算法的重構誤差最小。圖3 展示了30% 笛卡爾采樣模式下，Brain 圖像重構的細節放大圖及放大10 倍后的重構誤差圖（彩圖掃OSID 碼可見），第一行從左到右分別為：原圖、BM3D-IT-MRI 重構細節圖、PANO 重構細節圖、BM3DAMP-MRI 重構細節圖以及本文算法的重構細節圖；第二行從左到右分別為：30% 笛卡爾采樣mask、BM3D-IT 重構誤差圖、PANO 重構誤差圖、BM3D-AMP-MRI 重構誤差圖以及本文算法重構誤差圖。通過對比圖2 和圖3 結果可知，本文提出的重建算法能夠取得令人滿意的結果，重構后的磁共振圖像邊緣較清晰，視覺效果較對比算法佳。

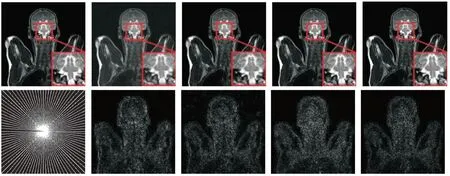
Fig.2 Experimental results（1）圖2 實驗結果展現（一）

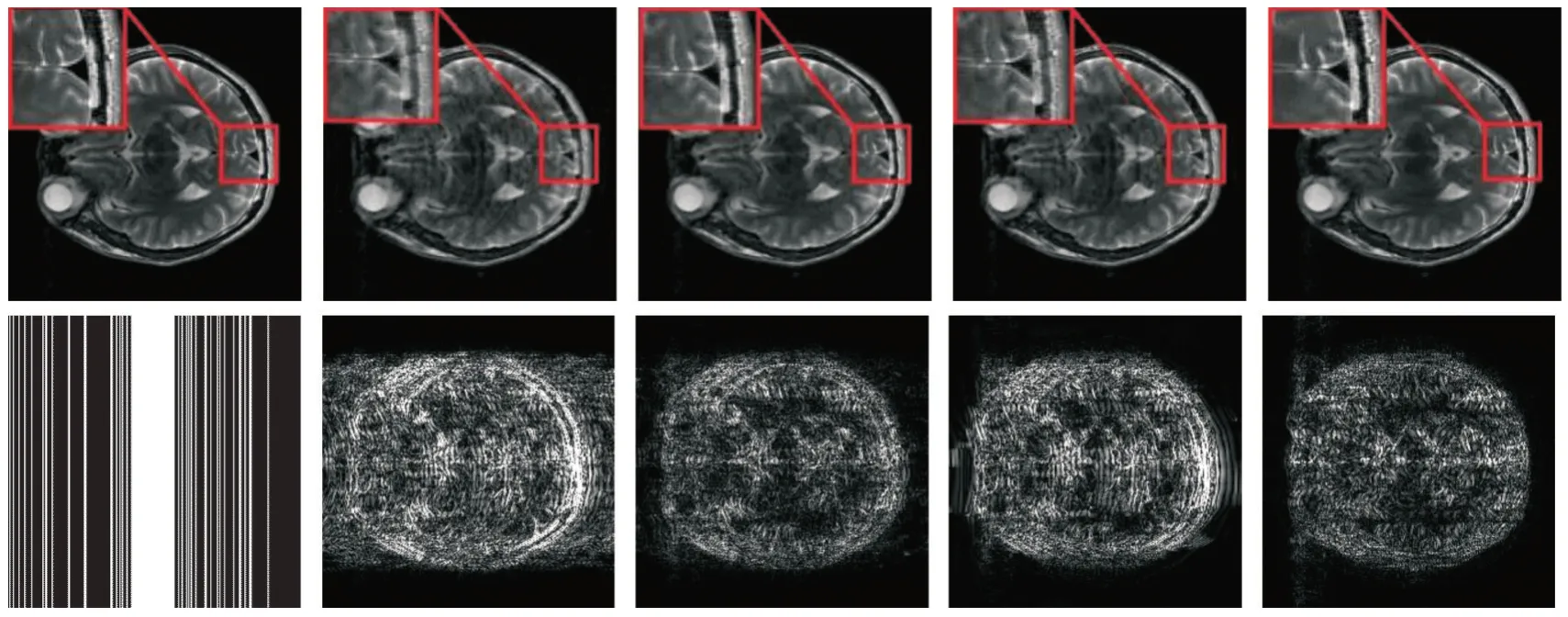
Fig.3 Experimental results（2）圖3 實驗結果展現（二）

采樣因子大小對重構算法會產生影響，采樣因子越大，圖像欠采樣率越低，表明欠采樣數據越低，采集到的原圖像有效信息越少。本文分別研究在采樣因子為2～10 的條件下，圖像重構質量變化情況。圖4（a）和圖4（b）展示了偽徑向采樣下，采樣因子對4 種算法重構質量的影響。觀察可知，當采樣因子增加時，重構的PSNR 值呈下降趨勢，同時RLNE 值呈增長趨勢，說明圖像重構質量在下降。

由圖4（a）和圖4（b）可知，本文算法與BM3D-AMPMRI 算法重構的PSNR 和RLNE 非常接近，兩者重構質量相當。但本文算法的重構性能明顯優于BM3D-IT-MRI 和PANO 算法。圖4（c）和圖4（d）展示了在笛卡爾采樣模式下，采樣因子對圖像重構的影響。同樣可以得出，采樣因子大小與圖像重構質量成反比。但是可以清晰地看出，本文算法重構的PSNR 值和RLNE 值明顯優于其它3 種算法。不同于偽徑向采樣，笛卡爾采樣條件下本文算法的重構性能明顯優于BM3D-AMP-MRI 的重建性能。一方面，表明本文算法在笛卡爾采樣模式下具有更加優異的重建性能；另一方面，說明不同的采樣模式對圖像重構結果有著至關重要的影響。

Fig.4 The PSNR and RLNE of reconstructed Brain image圖4 Brain 圖像重構的PSNR 與RLNE

3 結語

本文提出基于組稀疏殘差去噪的磁共振圖像重構算法，將組稀疏殘差作為去噪近似消息傳遞算法的去噪先驗，實現磁共振圖像重建。在Matlab 仿真平臺上，對比了3種磁共振圖像重建算法，研究不同采樣模式和采樣因子條件下，各算法的重建性能。實驗表明，本文提出的算法具有更高的PSNR 值和更低的RLNE 值，同時保留了原始圖像更多的細節信息，具有一定的應用價值。由于實際應用中，采集到的磁共振更多的是三維K 空間數據，因此，如何將本文算法拓展到三維動態磁共振成像中，是下一步研究的重點。