基于RC等效電路模型的鋰電池SOC估計

（江蘇大學電氣信息工程學院，江蘇鎮江 212000）

0 引言

鋰離子電池已成為新能源汽車的主流動力源之一，為延長電池使用壽命，必須對其進行科學、有效的管理［1］。荷電狀態（State of charge，SOC）能夠表征電池剩余電量，因此準確估算電池的SOC 已成為電動汽車電池管理系統（Bat?tery Management System，BMS）中的一個重要環節。然而，電池SOC 的估算精度依賴于電池電路模型及其相應的估計算法。

電池內部的電化學反應是一個復雜的非線性過程，很難用一個精確的電池模型準確表述電池性能［2］。常用的描述電池性能的方法有：等效電路模型法、電化學模型法、有限元模型法以及CFD 模型法等［3-4］。等效電路模型因具有簡單直觀、概念清晰、便于建模等優點，被廣泛應用于工程實踐中。文獻［5］分析蓄電池的Rint、Thevenin、PNGV、GNL 等電路模型的優缺點，但由于這些模型存在無法描述電池暫態響應，或響應精度不高、模型計算量過大等缺陷，無法適用于電動汽車在線SOC 估計；文獻［6］采用兩組阻容（Resistive-Capacity，RC）并聯網絡，能較好地描述鋰電池的暫態響應。

常用的電池SOC 估計方法有：①開路電壓法［7］。該方法需要將電池靜置一段時間后才能獲取準確的SOC，不能滿足實時估計的需求；②經驗公式及數學模型法［8］。其是在恒流充放電條件下總結出的規律，無法很好地適用于復雜的放電工況；③電化學阻抗頻譜法［9］。需要精密的電化學測量儀器，不能裝配到整車作實時估計；④神經網絡法［10］。需要大量數據進行訓練，估計結果受訓練數據及訓練方式影響較大；⑤安時積分法。將電流與時間的積分作為電池變化電量，把電池初始電量與變化電量差值相對電池總電量的百分比作為SOC 估計值，該方法能夠實現SOC的實時估計，也是目前應用最廣泛的SOC 估算方法。

本文基于雙阻容耦合的等效電路模型，通過HPPC 充放電循環實驗，以及最小二乘辨識方法確定模型中各個參數，結合EKF 算法與安時積分法估算單體鋰電池SOC。相較于傳統Thevenin 等效電路模型，將雙阻容耦合等效電路模型建立的空間狀態方程與安時積分算法相結合，估算的SOC 更高，且在恒流脈沖放電工況下誤差可保持在1% 以內。變流脈沖放電實驗結果表明，本文算法仍能有效修正SOC 估算初始誤差。

1 鋰離子電池等效電路模型

RC 模型是2001 年美國再生能源實驗室（NREL）發布的ADVISOR 軟件中采用的標準鋰電池模型（見圖1），該模型能夠描述電池變流充放電特性，且物理意義清晰，易于在工程中應用。

Fig.1 RC Equivalent circuit model圖1 RC 等效電路模型

圖1 中，電容Cb為電池化學儲能，Cc為電池表面電容，Rt為歐姆電阻，Re、Rc為極化內阻。根據基爾霍夫電壓定律，可建立RC 等效電路模型狀態方程如下：

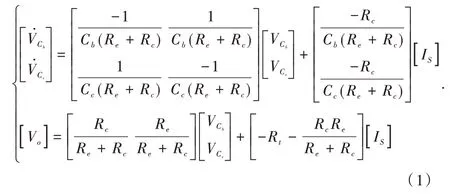
2 RC 電路模型參數計算

RC 電路中各等效元件參數值與SOC 的關系可由混合脈沖功率性能測試實驗HPPC［11］得到，一次脈沖放電測試過程中電壓變化如圖2 所示。

在給定的電池溫度和SOC 條件下，可選用基本物理學實驗值作為未知參數（Cb、Cc、Rt、Re、Rc）的初始值，從而進行數據處理與優化，確定狀態空間方程中的5 個參數值。

2.1 電池容量Cb 計算

電池容量Cb根據實驗過程中電池SOC 值在0%～100% 時的開路電壓與電池容量（A?h）變化率γ計算得出。即：

式中，Q為電池容量（A?h）。

2.2 電池表面電容Cc 計算

表面電容Cc與隨時間變化的電壓V3、V4，放電初始電壓V1（見圖2），以及時間常數τ相關。時間常數τ計算公式如下［11］：

式中，t2、t4分別為放電結束時間與開路電壓穩定時間。

表面電容Cc計算公式如下：

2.3 電阻Rt、Re、Rc 計算

為確定RC 電路模型中的電阻參數值大小，本文采取ADVISOR 的方法計算初始參數值。

模型中歐姆內阻Rt與極化內阻Rc、Re之間關系如式（6）所示。

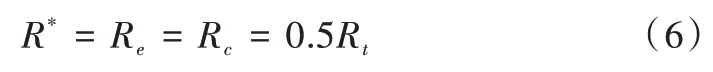
式中：

其中，Rbulk為單步長內電壓變化與電流的比值：

3 基于EKF 的SOC 估算方法

為減小SOC 估算誤差，本文將安時積分算法計算的SOC 值與RC 等效電路模型中的電容電壓作為系統狀態變量，構建狀態方程，并將RC 等效模型中的開路電壓值Vo作為觀測變量，構建觀測方程。通過迭代計算，使任意時刻SOC 的估計值均可通過觀測值修正，從而提高估計精度。

3.1 安時積分法

安時積分法是最常用的SOC 估算方法，但由于存在SOC 初始誤差和電流累計誤差等問題［1］，隨著算法的運行，SOC 估算誤差會逐漸增加。安時積分法計算公式如下：

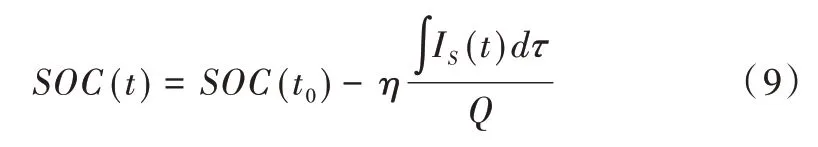
式中，η為庫倫效率，由放電容量與充電容量的比值計算得到；Q為標準放電測試下的靜態容量；IS為充放電電流。

3.2 EKF 算法應用

結合EKF 算法與安時積分算法，SOC 估計步驟如下［12］：

步驟1：建立電池模型狀態方程。

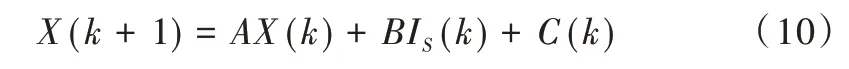
其中：

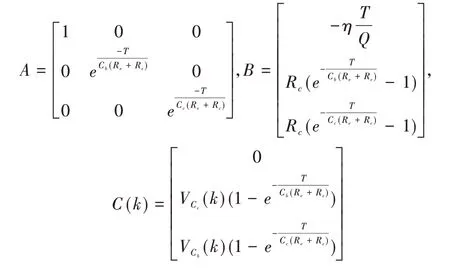
步驟2：建立電池模型觀測方程。選取k時刻電池端電壓Vo(k)為觀測量，可得觀測方程為：

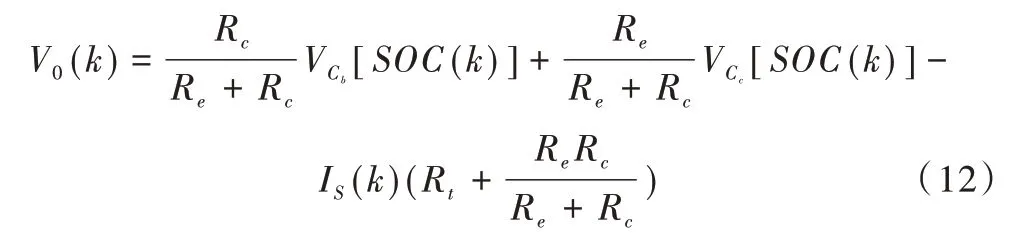
由于模型參數Rt、Re、Rc的取值與SOC 有關，且經過實驗驗證，SOC 對模型參數的影響較小［13］，為減小計算量，該值可忽略不計。此外，由于相對于更容易獲取，代表電池無負載時電池開路電壓，其函數關系可通過放電實驗數據擬合得到。因此，在觀測方程中不再考慮與SOC 的函數關系，可將觀測方程（12）簡化為：

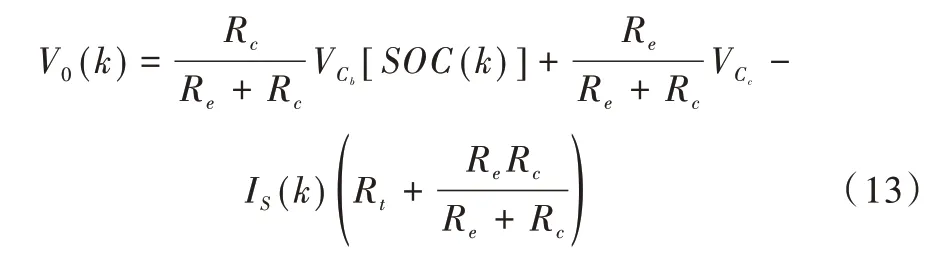
步驟3：對狀態方程和觀測方程進行線性化處理。

由于觀測方程是非線性方程，為了便于EKF 估計，采用泰勒近似，即：

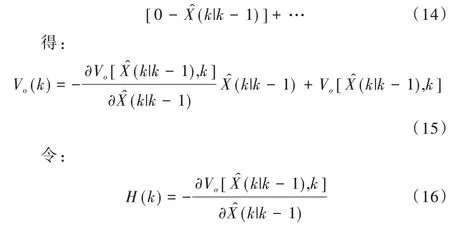
設測量矩陣H為：

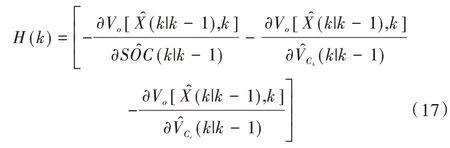
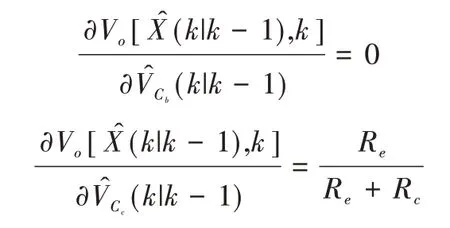
步驟4：參數初始化與循環遞推［14］。

（1）參數初始化：

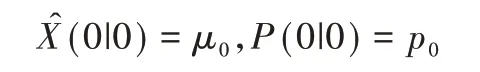
（2）狀態變量更新：

（3）觀測變量更新：

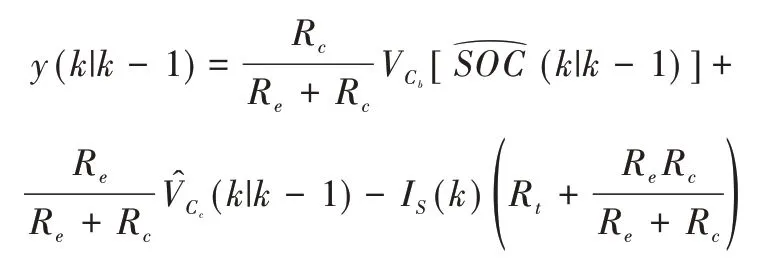
（4）計算誤差協方差矩陣：

（5）計算kalman 增益Kg：

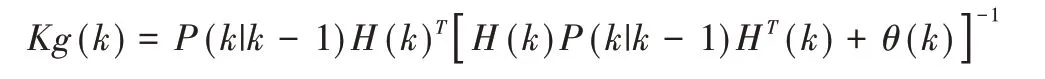
（6）計算狀態變量最優估計值：

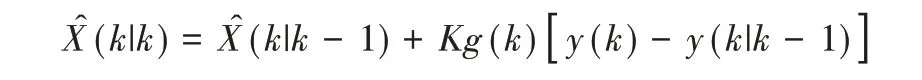
（7）更新誤差協方差矩陣：

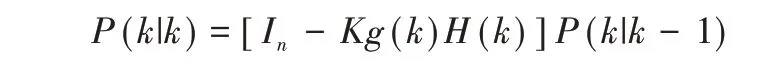
在上述遞推過程中，y(k)=Vo(k)，In為n階單位陣，w(k)、θ(k)分別為零均值且符合高斯分布的系統噪聲和觀測噪聲協方差，μ0為狀態變量初始值，p0為初始誤差協方差。

基于EKF 算法的SOC 估算流程如圖3 所示［6］。

Fig.3 SOC Estimating process圖3 SOC 估算流程

4 實驗驗證

本實驗采用國內某廠家生產的便攜式鋰電池充放電機（見圖4）進行充放電實驗，通過上位機控制充放電電流與充放時間，利用放電實驗確定國內某廠商生產的18650型號的磷酸鐵鋰電池在實驗環境下的標準容量Q與特定放電工況下的庫倫效率η。采用第2 節中計算模型參數的方法并結合最小二乘法［15-20］，計算RC 等效模型中各參數最優值。本文選取恒流脈沖放電與變流脈沖放電實驗驗證該算法對SOC 的估算效果。

Fig.4 Portable lithium battery charging and discharging machine圖4 便攜式鋰電池充放電機

4.1 參數識別

本次參數辨識采用的標準電壓為3.7V，額定容量為2 800mAh 的鋰電池。在不同放電電流下對實驗電池進行放電，獲得電池實際容量如表1 所示。

因大電流放電導致電池端電壓迅速下降至放電截止電壓（設定值2.75V），待靜置后以小電流放電，仍可釋放出剩余電量。將前后兩次放電量總和記為電池可用容量，放電流程如圖5 所示。

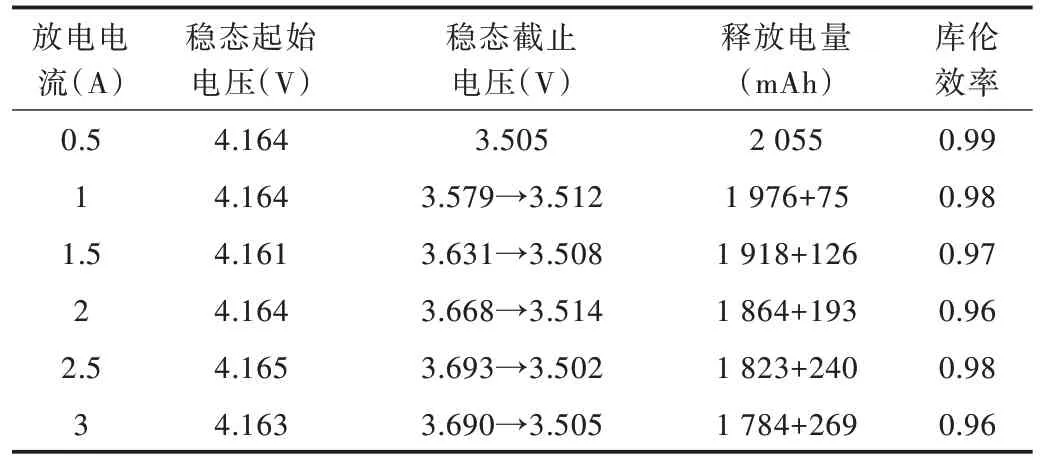
Table 1 Battery capacity and Coulomb efficiency表1 電池容量與庫倫效率

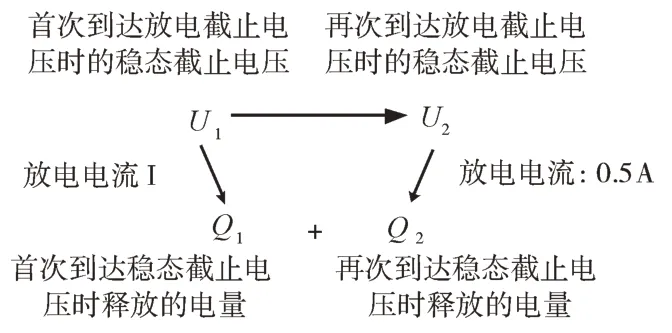
Fig.5 圖5 放電流程

取平均釋放容量為電池可用容量，即Q為2 054mAh；取放電電流區間［0.5 3］內平均庫倫效率為電池庫倫效率，即η為97.3%。

通過控制容量釋放，在不同SOC 值下利用HPPC 脈沖放電實驗獲取電池電壓端的電壓變化曲線，對模型參數進行最小二乘估計，結果如表2 所示。

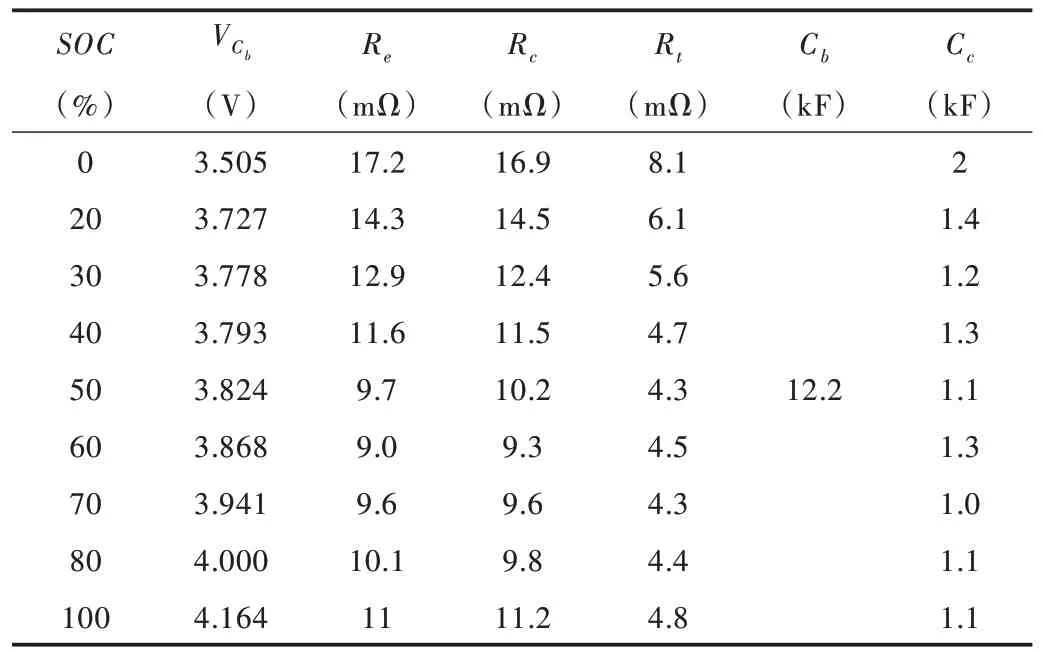
Table 2 Parameter identification results表2 參數辨識結果

對SOC與進行4 次擬合，SOC與的關系如圖6所示。

Fig.6 SOC and the open circuit voltage圖6 SOC 與開路電壓關系

SOC與的函數關系如式（18）所示。

因模型參數Re、Rc、Rt對SOC 估算的影響可忽略不計，為簡化方程，降低計算量，取各參數辨識結果的平均值作為參數最終取值，結果如表3 所示。

Table 3 Resistance parameter value表3 電阻參數取值

結果表明，Re、Rc、Rt3 個參數之間的關系與式（6）基本一致，因此由式（4）、式（5）計算得出表面電容Cc的值如表4 所示。取表面電容平均值1.1kF作為參數Cc的最終值。

Table 4 Surface capacitance value表4 表面電容取值

4.2 恒流脈沖放電實驗

恒流放電脈沖放電實驗中，取恒定放電電流為1A，每次脈沖放電時間為10s，放電結束后靜置10s，如此循環放電。放電電流如圖7 所示。

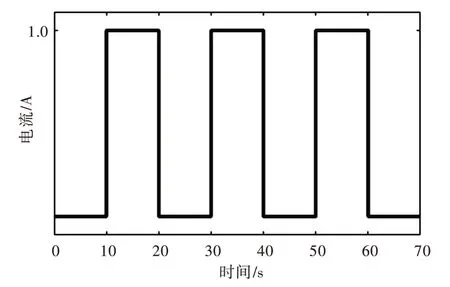
Fig.7 Constant current pulse discharge current圖7 恒流脈沖放電電流

設置采樣周期為10s，共進行1 000 次采樣，SOC 初始值為100%。為體現本文算法對SOC 初始誤差的修正作用，設置濾波初始值分別為100%、82%、56%。恒流脈沖放電結果如圖8 所示。

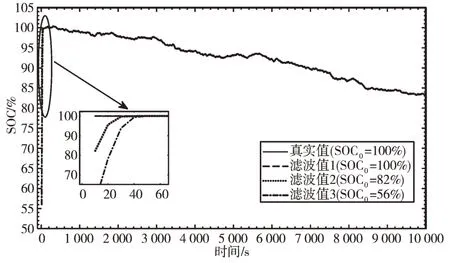
Fig.8 SOC The EKF estimate and true value of SOC圖8 SOC 的EKF 估計值與真實值

EKF 估計結果與真實值相對誤差如圖9 所示。

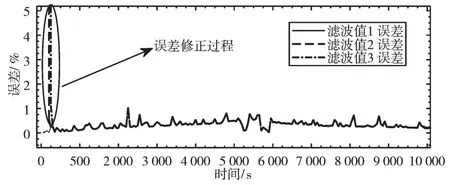
Fig.9 SOC estimation error圖9 SOC 估算誤差

恒流放電實驗結果表明，EKF 算法對SOC 初始誤差能夠進行快速修正，且能將SOC 估算相對誤差維持在1% 以內，具有較高的估算精度。

4.3 變流脈沖放電實驗

變流放電脈沖放電實驗中，取放電電流分別為1A、2A、3A，且每次脈沖放電時間為10s，放電結束后靜置10s，如此循環放電。放電電流如圖10 所示。

Fig.10 Variable current pulse discharge current圖10 變流脈沖放電電流

設置采樣周期為10s，共進行1 000 次采樣，SOC 初始值為100%。同樣設置濾波初始值分別為100%、86%、58%。變流脈沖放電結果如圖11 所示。

Fig.11 The EKF estimate and true value of SOC圖11 SOC 的EKF 估計值與真實值

EKF 估計結果與真實值相對誤差如圖12 所示。

Fig.12 SOC estimation error圖12 SOC 估算誤差

變流放電實驗結果表明，EKF 算法同樣能修正SOC 估算初始誤差，但由于采用較大的放電電流，導致電池溫度迅速增加，致使SOC 估算誤差也逐漸增加。因此，在對模型參數進行辨識的同時，還應考慮溫度的作用。

5 結語

本文建立動力鋰電池的RC 等效電路模型并進行模型參數辨識，同時建立電池狀態方程與觀測方程，采用EKF與安時積分相結合的算法對SOC 進行實時估計，通過實驗驗證得出以下結論：

（1）具有RC 網絡的等效電路模型能夠較好地體現鋰電池在充放電過程中的動態響應，其模型參數的辨識結果較為精準，滿足應用要求。

（2）EKF 與安時積分相結合的算法對SOC 初始誤差具有良好的修正作用，其SOC 穩態調節誤差時間與初始絕對誤差呈正相關。

（3）間接驗證了溫度對模型參數的影響，由溫度引起的模型參數變化是導致SOC 估算誤差逐漸增加的原因。