CST 中四態非厄米系統耦合模理論研究

（上海理工大學 理學院，上海 200093）

0 引言

厄米系統是保守的，不與外界發生能量交換且不具有增益和損耗。與之相反，非厄米系統具有增益或損耗，是開放邊界條件的系統，其物理量通常用非厄米算符描述。非厄米算符的本征值一般是復數［1］，非厄米系統與厄米系統的一個明顯區別是非厄米系統存在奇異點（Exceptional Point，EP）。在奇異點處，非厄米系統本征值和本征態同時發生簡并合并。奇異點附近通常伴隨著能級排斥、交叉、相位突變等異常光學現象，所以在單向無反射傳輸、損耗誘導透明、微型激光器、超靈敏傳感等領域具有十分重要的應用［2-8］。奇異點概念最先由Kato［9］提出，研究人員通常使用兩個耦合的諧振單元構建并研究二態非厄米系統，從立體微波腔、耦合電子電路系統，再到光學腔、原子腔等［10-15］。在此基礎上，Ding 等［16］利用四階哈密頓矩陣分析4 個耦合聲學微腔組成的四態非厄米系統；程時航等［17］利用矩陣本征值研究四態微環耦合系統；Hossein 等［18］利用三階矩陣研究光學微環組成的高階非厄米系統。然而利用耦合模理論研究高階非厄米系統的工作仍然較少。本文在二態系統的耦合模理論基礎上［19-21］，將耦合模理論推廣至四態非厄米系統，從理論上分析四態系統的傳輸系數。在CST 仿真軟件中設計雙開口諧振環，以4 個雙開口諧振環組成四態非厄米系統。利用時域有限差分法模擬此系統的傳輸系數，結果表明仿真與理論分析吻合。

1 模型設計與分析

構建如圖1 所示四態非厄米系統，此系統含有4 個諧振單元：A，B，C，D。其中直接與入射波（光）耦合的“亮態”諧振單元由Port j 入射，j=1.2）、“暗態”諧振單元（不能直接被入射波（光）激勵，而是與諧振單元耦合）為一組，具有相同的諧振頻率ω1，組內耦合系數為K。同理為一組，具有相同的諧振頻率ω2，組內耦合系數也為K。兩組諧振單元之間引入組間耦合系數t'。之間沒有近場耦合。

Fig.1 Four state non Hermitian system model圖1 四態非厄米系統模型

四態非厄米系統四端口相干激勵時，基于耦合模理論的運動方程表示如下：

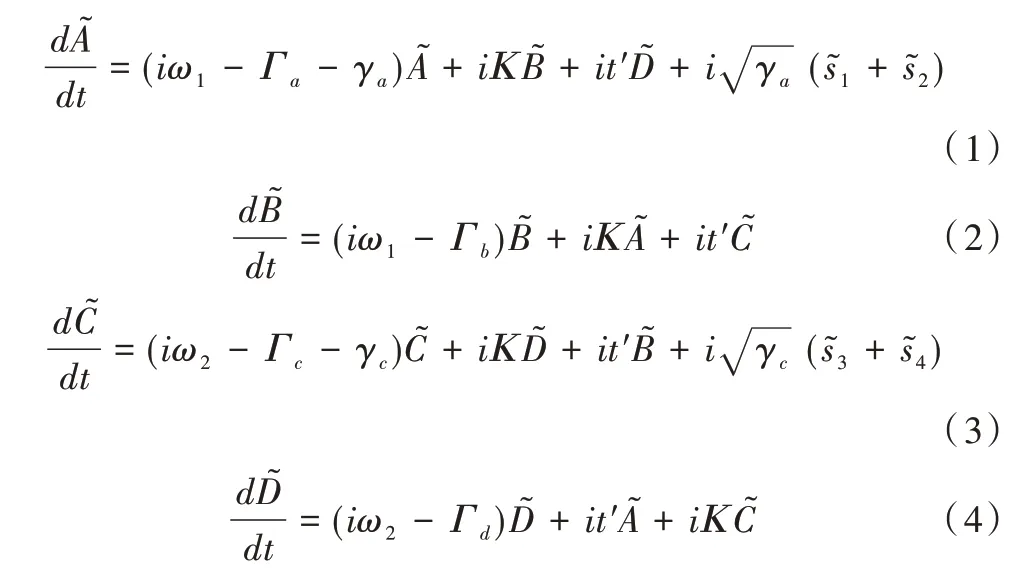
Γa，Γb，Γc，Γd分別是諧振單元A，B，C，D 的耗散損耗，γa，γc分別是“亮態”諧振單元A，C 的散射損耗。其中。式（1）中，第一項表示“亮態”A 在散射損耗γa、耗散損耗Γa下的諧振，ω1為“亮態”原子的中心頻率；第二項表示“亮態”A 和“暗態”B 原子間的組內耦合；第三項表示“亮態”A 和“暗態”D 間的組間耦合；第四項表示“亮態”A 與入射波（光）的耦合。式（3）同理。式（2）中，第一項表示“暗態”原子在耗散損耗Γb下的諧振，ω1為諧振環的本征頻率；第二項表示“暗態”B 與“亮態”A 間的組內耦合；第三項表示“亮態”C和“暗態”B 間的組間耦合。由于“暗態”原子無法與入射波（光）直接耦合，因此沒有第四項，式（4）同理。

當入射波只從Port1 入射時，方程如下：

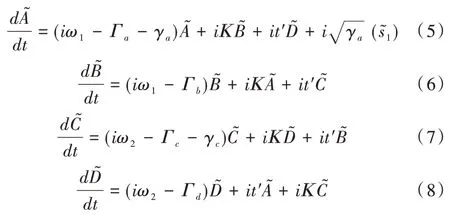
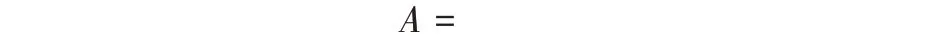
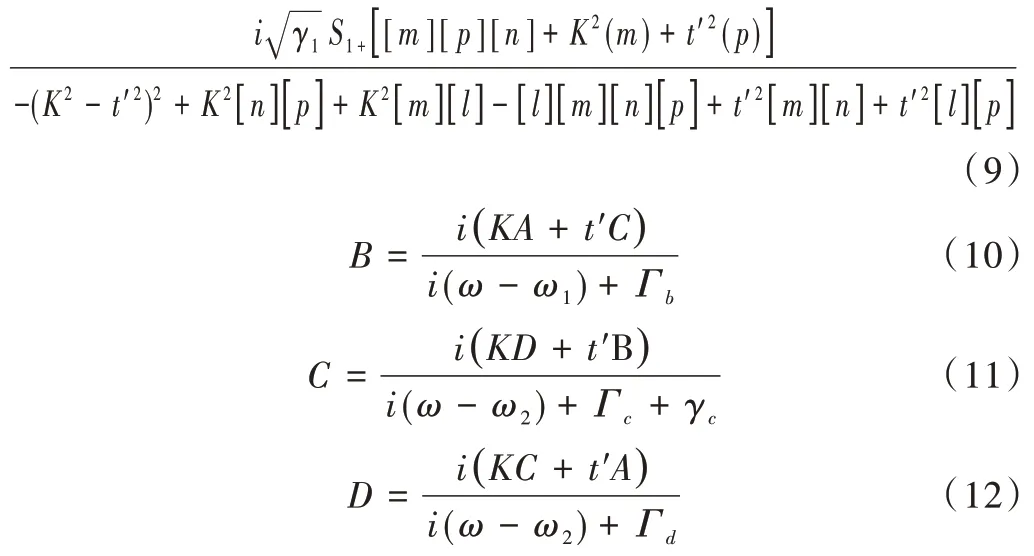
其中

四態非厄米系統的傳輸系數如下：

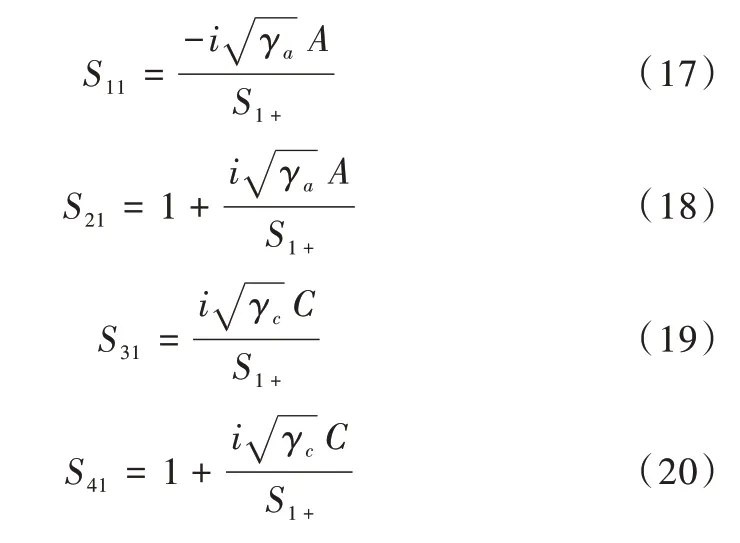
2 仿真實驗及結果

為驗證以上理論分析的正確性，利用時域有限差分法仿真分析四態非厄米系統。圖2 給出四態非厄米系統的仿真結構，在諧振環開口處加載電子元器件如電容、電阻。控制諧振環的共振頻率ω1與耗散損耗Γ、諧振環之間的距離決定組內耦合強度K和組間耦合強度t'。上述參數確定方法如下：通過電磁場仿真軟件CST 得到單個諧振環的本征頻率以及損耗特性；然后加入暗態諧振環構成耦合的二態非厄米系統實驗，研究原子間的耦合強度特性。

圖2 中含有4 個雙開口諧振環和上下兩個微帶線。雙開口諧振環尺寸大小為13.2 mm*7.8 mm，銅線寬0.8 mm，諧振環上端寬度為4.04 mm，兩側設計為45°斜線，可與相鄰諧振環進行耦合。上下微帶線寬度為2.4 mm，諧振環與微帶線距離為0.2 mm。基板材料為聚四氟乙烯，相對介電常數εr=2.2，基板厚度為0.787 mm，雙面覆銅。每個開口諧振環上都加載一個電容與一個電阻。使用CST 仿真可得到單個諧振環上加載不同電容值時的本征頻率ω1，如圖3 所示。環上加載的電容大小決定諧振環本征頻率。在單個諧振環上加載不同電阻時的反射譜如圖4 所示。電阻越大，反射率峰值越低，反射率的半高寬越大，即損耗越大。電阻值與損耗進行線性擬合得到“亮態”諧振環的耗散損耗Γ=0.014 5*R GHz，散射損耗γ=0.013 6 GHz。其中R為開口環加載的電阻大小。

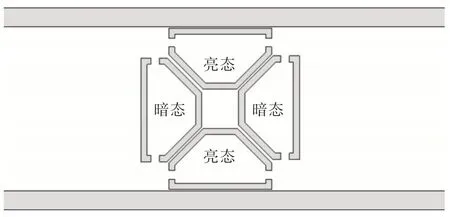
Fig.2 State the Hermitian system structure圖2 四態非厄米系統結構

Fig.3 Different load capacitance in the resonant ring reflection spectrum圖3 在諧振環上加載不同電容的反射譜

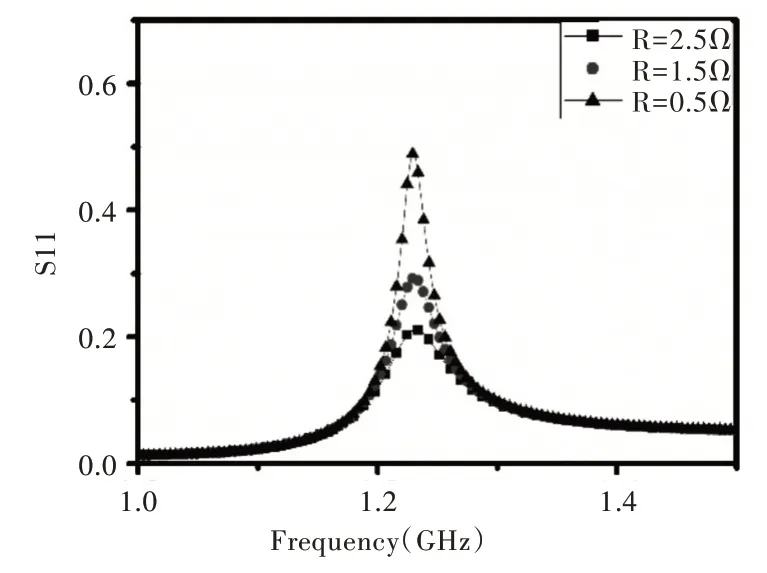
Fig.4 On resonant ring loading the reflection spectrum of different resistance圖4 在諧振環上加載不同電阻的反射譜

在計算耦合強度時需引入“暗態”諧振單元，由兩個開口諧振環組建二態系統。使用CST 仿真軟件計算加載相同電容值1.2 pf 的二態系統反射譜線，結果如圖5 所示。其中耦合強度等于反射譜峰值頻率差的二分之一，隨環間距s 從0.6 mm 減小至0 mm，反射譜線的兩個峰間距增大，即耦合強度增大。

使用CST 電磁仿真軟件，計算加載1.2 pf 電容的開口諧振環四態非厄米系統加載電阻為1 Ω 時的傳輸譜線，如圖6 所示。前述計算可得四態非厄米系統中的各種參數，4 個諧振環都加載1.2 pf 電容時，諧振環本征頻率ω1=1.24 GHz，加載電阻為1 Ω 時，耗散損耗Γ=0.014 5 GHz和散射損耗γ=0.013 6 GHz。四態系統組內間距為0.2 mm，組間間距為0.4 mm 時，組內耦合強度K=0.045 GHz，組間耦合強度t'=0.025 GHz，將各類參數帶入耦合模方程得非厄米系統的S 參數及實部虛部，如圖7 所示。對比CST 仿真數據圖6 和數值模擬圖7（c），結果基本一致。

Fig.5 Binary system under the different spacing of reflection spectrum圖5 二態系統不同間距下的反射譜

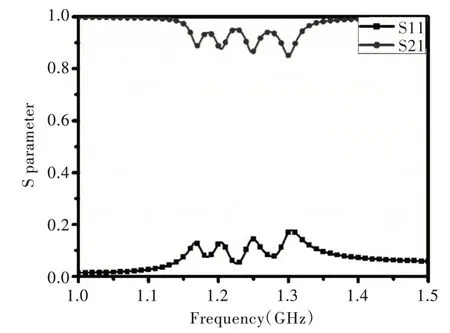
Fig.6 CST simulation of four state system transmission line圖6 CST 仿真的四態系統傳輸譜線

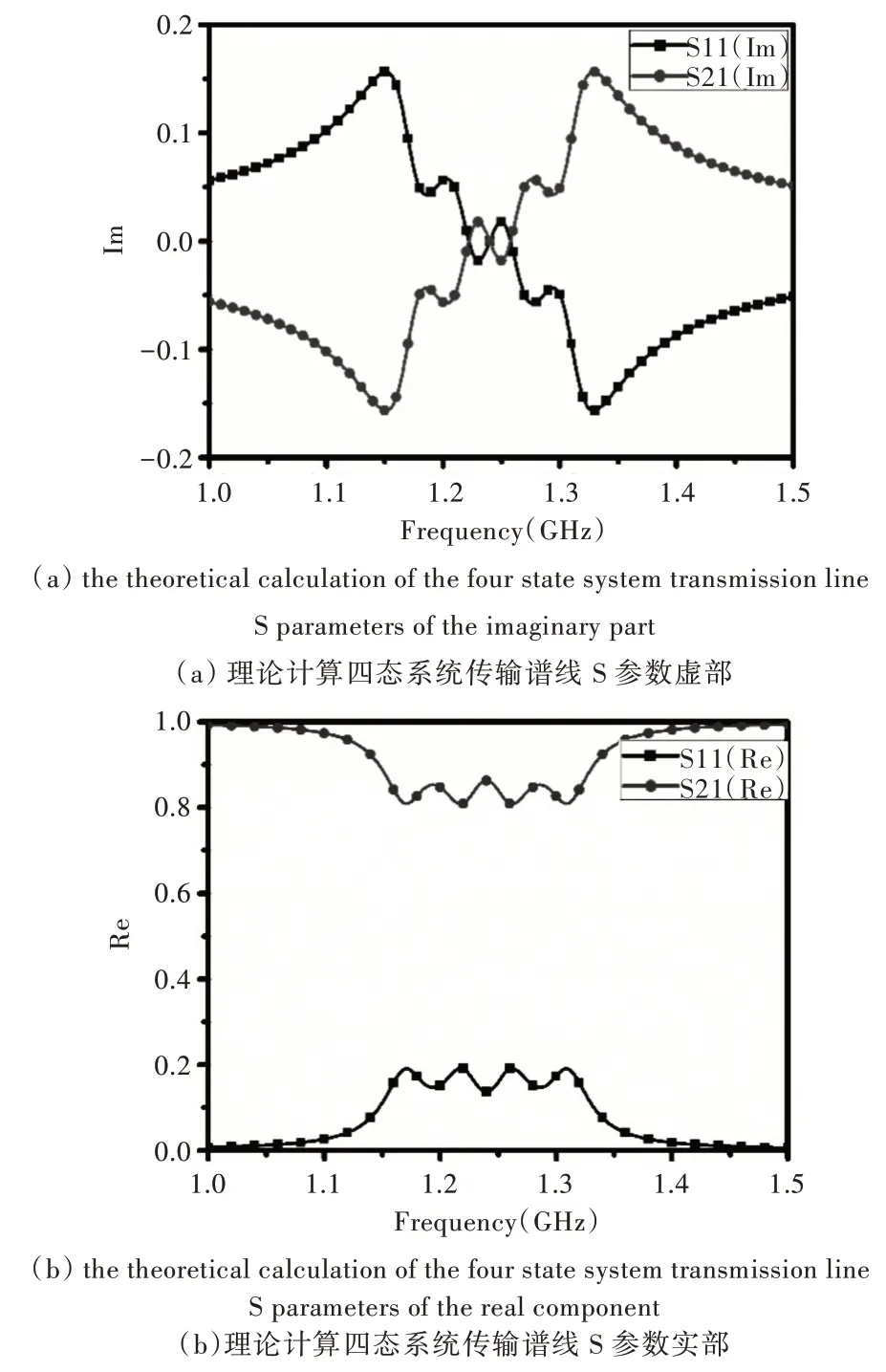
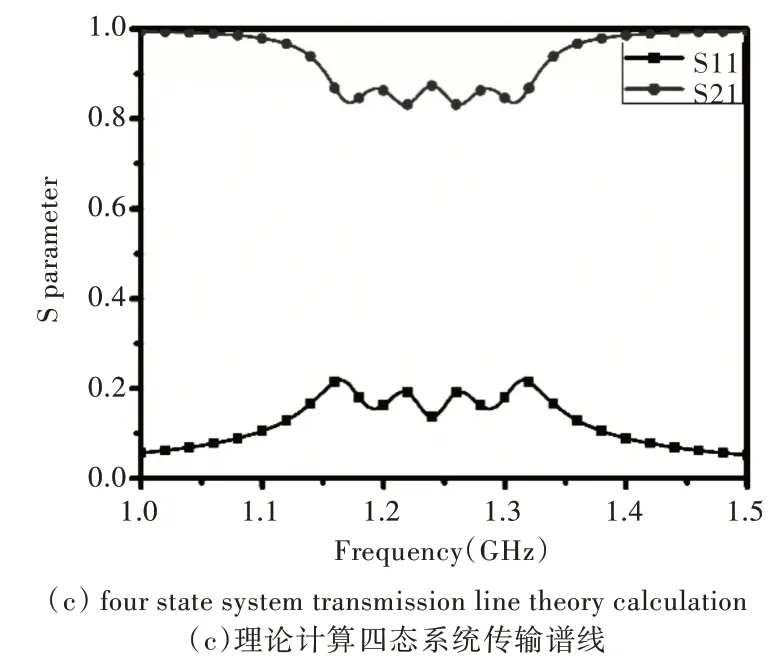
Fig.7 The numerical simulation圖7 數值模擬

3 結語

本文基于CST 仿真軟件設計并仿真了四態非厄米系統，研究了系統中諧振頻率為1.24GHz 的諧振單元損耗與耦合強度，并分析了四態非厄米系統耦合機制，利用耦合模理論計算了系統傳輸系數。仿真結果和數值計算一致，驗證了耦合模理論處理四態非厄米系統問題的可行性。本文的四態耦合模理論可以用于分析光子晶體系統、光纖微環系統等不同頻段的四態非厄米系統。同時在仿真中發現隨著加載電容的變化，諧振環損耗有誤差，后期可通過擬合減少誤差。