基于量測數據的外部電網在線等值實用方法

肖 健，甘 明，劉有志，資 慧，林濟鏗

（1. 廣東電網有限責任公司廣州供電局,廣東省廣州市510620；2. 同濟大學電子與信息工程學院,上海市201804）

0 引言

電網作為一個一體化運行的復雜系統,完備及準確的電網信息是進行系統狀態分析、評估及控制的基礎［1-2］；而分級分區的管理又是中國電網的典型管理模式,各個電力公司分屬于不同的主體,既合作又競爭。相應地,就存在著準確及完備的信息需求與管理權限之間的矛盾：一方面,不同的電力公司為了實現準確的電網分析及控制,需要相鄰網絡的準確及完備的信息,而相鄰網絡又屬于另一電力公司管轄,因信息的保密性或經濟利益等方面的考慮,往往不愿意完全公開其相應完備的準確信息,或只能公開部分信息［3］；另一方面,相鄰電網傳遞來的信息存在與本管轄網絡內的信息采集時刻一致性問題,對于系統分析及控制的有效性會帶來一定的影響［4］,甚至會出現包括潮流計算不收斂［5］等問題,相應也給本管轄電網運行的安全性和穩定性帶來一定的風險。面對該矛盾,準確的外部電網（簡稱外網）等值策略即成為最為有效的應對策略,即在只有部分外網或相鄰網絡的信息條件下,給出外網較為準確的等值網絡,以此完成本網絡準確的分析及控制,這也成為一個備受關注的研究課題。

目前,外網等值方法大致可分為2 類。

1）外網信息已知的拓撲法等值。在外網信息已知的情況下,可以通過包括簡單掛值機法［6］,戴維南［7］、諾 頓 等 值 法［8］,Ward 等 值［9］、REI 等 值［10］及 其改進方法等［11-12］,對外網做出較為準確的等值。該類方法相對比較成熟,在一個狀態下的等值精度很高,但當內部電網（簡稱內網）的結構發生較大變化時,如何保證等值準確性還有待進一步改進。

2）外網信息未知或部分已知的非拓撲法等值。該類方法的基本思路是基于內部系統的數據采集與監 控（supervisory control and data acquisition,SCADA）量測數據,采取各種策略估計出外網等值參數。文獻［13-14］提出了單端口戴維南等值方法,即采用一個電壓源串聯一個阻抗來進行外網等值,通過建立邊界節點處的多時段量測方程來求解等值參數；但該方法只能適用于單端口網絡的等值。文獻［15-16］提出了基于簡化Ward 等值方法,僅考慮邊界節點的等值線路與等值注入功率,并通過多次內網支路開合操作獲得潮流狀態數據,采用最小二乘法估計簡化Ward 等值參數。但該方法較難應用于在線等值,因為在實際運行時往往不允許對內網進行非計劃的頻繁開關操作。文獻［17］提出一種基于實測信息的兩端口靜態等值方法,該方法無須進行內網開斷操作,但僅適用于內外網間僅含2 個邊界節點的網絡。文獻［18］提出一種兩階段的多端口靜態等值方法,首先估計簡化Ward 等值模型參數,進而估計擴展Ward 等值模型參數；因采用分步求解策略,降低了第2 階段各等值參數之間的耦合,在一定程度上提高了等值準確性。但該方法的優化計算方法是無約束的,存在所估計得到的網絡參數有可能為負的問題,從而導致后續的潮流計算收斂困難等問題。

基于如上綜述,本文提出了基于內網量測數據的外網在線等值新方法。該方法有如下特點：①等值網絡包括邊界節點間的耦合支路及外網與每一邊界節點的等值阻抗及電源,可以有效反映外網對內網的影響；②采用基于最大及最小運行方式下的Ward 等值網絡相應等值支路的阻抗值作為在線等值網絡參數范圍約束,使等值網絡支路參數結果位于合理區間；③當時段間的量測數據差別不大時,本文提出基于歷史信息的量測補充獲取策略,以克服不被允許的非計劃線路開斷的策略,相應提升了參數估計的穩定性和可靠性,進而提升了方法的工程實用性。

1 基于量測數據的在線等值網絡及模型

1.1 等值網絡

將整個系統劃分為如圖1 所示的外網、邊界節點和內網［17］。對于外網,基于戴維南等值思想,將其等值為多電源網絡。該等值網絡包括每一邊界節點通過一個支路與等值電源相連,邊界節點之間通過等值支路相連。等值之后的網絡如圖2 所示。

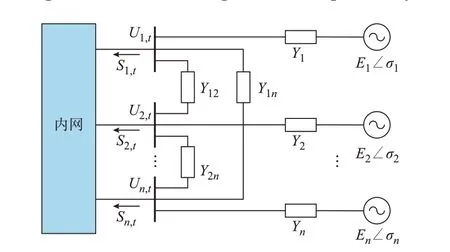
圖1 等值前的互聯網絡Fig.1 Interconnected grid before equivalency

圖2 中：Ui,t(i=1,2,…,n)為t時刻內網邊界節點i的電壓幅值,其中n為邊界節點個數；Si,t=Pi,t+jQi,t為t時刻從邊界節點i注入內網的視在功率,其中Pi,t和Qi,t分別為t時刻邊界節點i流入內網的有功和無功功率,t=1,2,…,m,m為邊界節點量測時段數；Yij=Gij+jBij為邊界節點i和j之間等值線路的互導納,其中Gij和Bij分別為電導和電納值；Yi=Gi+jBi為邊界節點i與對應的等值發電機節點之間的互導納,其中Gi和Bi分別為電導和電納值；Ei和σi分別為等值發電機i的內電勢幅值和相角。

1.2 等值網絡參數求解的優化模型

對于圖2 所示的等值網絡,其邊界節點的功率及節點電壓在等值前后必須一致,即

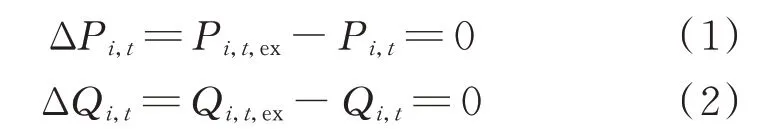
式中：ΔPi,t和ΔQi,t分別為t時刻邊界節點i的有功和無功功率失配量；Pi,t,ex和Qi,t,ex分別為t時刻外網流入邊界節點i的等值有功和無功功率,分別如式（3）、式（4）所示。

式中：n≥2；θij,t=θi,t-θj,t,θi,t和θj,t分別為邊界節點i和j的電壓相角；θie,t=θi,t-σi。

式（3）和式（4）中,待估計變量包括：Ei,σi,Gi,Bi,Gij,Bij(i,j=1,2,…,n),為方便起見記為如下向 量 ：xi=[Ei,σi,Gi,Bi]；yij=[Gij,Bij]；i=1,2,…,n；j=i+1,i+2,…,n；i≠j。

為了實現等值網絡參數的良好估計,本文基于內網的多個時間斷面的SCADA 量測,構建以邊界節點等值網絡計算值與量測值之差（即失配量）的平方和最小為優化目標,以等值支路的參數xi,yij位于一定范圍內為約束條件的優化模型。具體表達式為：

式中：i,j=1,2,…,n；xi,3和xi,4分別表示Gi和Bi,xi,3,max,xi,4,max和xi,3,min,xi,4,min分別表示該互導納的上限 和 下 限；yij,1和yij,2分 別 表 示Gij和Bij,yij,1,max,yij,2,max和yij,1,min,yij,2,min分別表示該互導納的上限和下限。關于互導納的上下限約束將在下文詳細說明。

2 等值網絡模型的求解

2.1 不等式約束條件的確定

式（5）中的不等式約束的目的是使得待求等值網絡的參數處于可行范圍內,否則若初值選擇不合適,就很可能使得等值網絡參數出現負值等不合乎實際的解,也相應使得后續的基于該等值網絡的潮流計算出現不收斂等問題。文獻［19-20］雖給出了等值支路的電阻、電抗大于0,或上下限約束,但大于0 的約束過于寬泛,仍存在阻抗值過小導致潮流計算收斂困難等問題,且并未給出上下限如何確定的具體方法。由于當前的外網運行方式下網絡負載必然處于其最大、最小運行方式之間,因此,本文提出當前運行方式下各等值支路的阻抗值也位于2 種運行方式下相應等值支路的阻抗值之間。

等值支路上下限的具體確定方法如下：對于既定的當前內網所在的完整電力系統,獲取其最大、最小運行方式下的外網拓撲結構及機組出力,結合當前內網,分別對其進行Ward 等值,把相應的等值網絡轉化為圖2 所示的等值網絡,所得到的等值網絡2 組支路參數,即為當前對應等值網絡中相應支路的上下限。

需要指出的是,各個電力公司均要在協同模式下制定年度運行方式,因此,相應外網的最大、最小等典型運行方式是可以得到的。

2.2 基于歷史數據獲取補充量測數據

如式（5）所示的基于內網多時段量測數據的等值網絡參數求解模型,本質上是假定在時間間隔不長的情況下,外網的結構及負荷不發生大的變化或無變化,只有內網結構及負荷發生變化,然后采用邊界量測數據來獲得外部系統的準確等值網絡。雖然外部系統在時間間隔短的情況下確實不會發生明顯的變化,但內部系統也可能不發生明顯的變化,從而使得邊界的量測值在相近的幾個時段差別不大。在這樣的情況下,對于式（5）的求解,因迭代線性方程組的系數矩陣“條件數”會很高,導致迭代的收斂性很差,或不收斂,即使收斂其所計算得到的等值參數也非常不準確。研究表明,不同量測時段之間量測值變化量百分比均值γ＜0.01%時,等值參數估計已呈現出非常不穩定或不收斂的情況［21］。

為克服上述問題,正如引言所指出的,文獻［15-16］采用內網的直接支路開合操作來獲得可用的邊界量測數據,而實際系統并不允許對于內網支路進行非計劃的任意開合。為使方法更具有工程實用性,本文提出了基于歷史信息來獲得有效的量測數據的策略,以避免實際工程中難以實施的對內網支路直接進行非計劃的開合操作。

由于各電力公司均要在協同模式下制定年度運行方式,且電力系統每間隔一定時間會傳輸一次外網量測數據,因此可以獲得外網歷史量測數據,且歷史數據服從多維正態分布。外網量測數據傳輸間隔通常為3～5 min,這一時段內外網結構基本不變。以等值開始前的最后一次外網量測值為當前外網量測基準,若某一歷史時段外網量測數據與之接近,則兩時段間外網結構及負荷接近,邊界節點量測值差異主要源于內網。歷史數據期望-h和方差-C分別為：

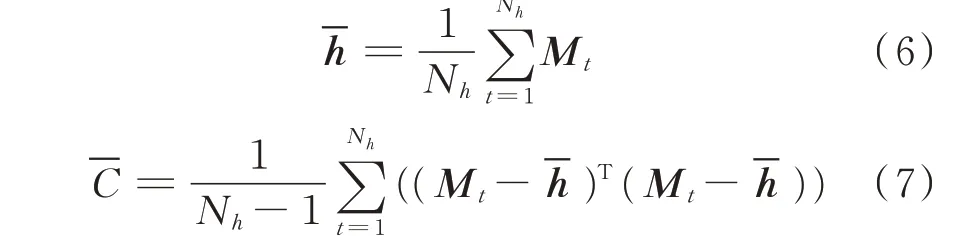
式中：Mt為第t個歷史時段外網量測數據向量；Nh為歷史數據時段總數。

定義歷史數據與當前時段最新外網量測的馬氏距離（Mahalanobis distance,MD）為：

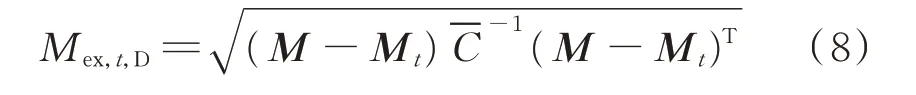
式中：Mex,t,D為第t個歷史時段外網量測與當前時段最新外網量測的馬氏距離；M為當前時段最新外網量測數據向量。

與當前時段最新外網量測接近的歷史時段集合為ψ,滿足

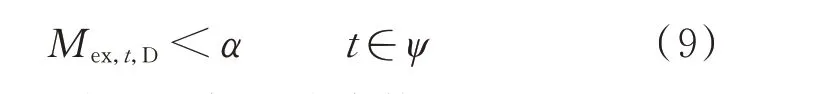
式中：α為馬氏距離的下側四分位數。

進而,在集合ψ內選擇與當前時段內網拓撲結構最接近的歷史時段,即與當前時段內網導納矩陣馬氏距離最小的時段,以該歷史時段邊界節點量測值用于式（5）等值網絡參數估計模型求解,從而有效提高參數估計收斂性。歷史時段內網導納與當前時段內網導納的馬氏距離為：

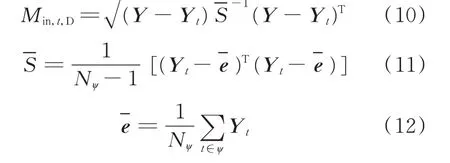
式中：Y為當前時段內網導納矩陣展平后一維向量；Yt為第t個歷史時段內網導納矩陣展平后一維向量；Nψ為集合ψ內的時段總數。

2.3 基于內點法的等值模型求解過程

采用內點法進行在線等值網絡模型求解,該方法已在商用求解器IPOPT 中實現［22］,可直接調用。求解過程如下。

步驟1：確定在線等值網絡參數邊界。根據最大、最小典型運行方式下的全網數據,采用Ward 等值模型,求解典型運行方式下的等值參數,并把Ward 等值網絡轉換成圖2 所示網絡,相應等值支路的2 個運行方式下的支路參數即為對應等值網絡參數估計的上下限約束。

步驟2：確定所需量測時段數。假設邊界節點總數為n,則等值網絡參數總數為（n2+3n）,m個量測時段可獲得量測方程2mn個。為保證等值網絡參數的可估性,需滿足量測方程數大于待估計參數,即

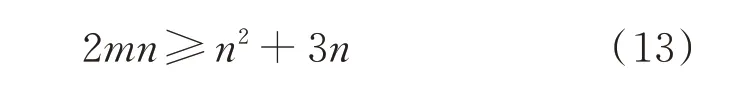
根據式（13）所示原則確定所需量測時段數m。

步驟3：采集初始時段內網量測數據。

步驟4：若已經采集m個時段量測數據,進行步驟6,否則采集下一時段量測數據并與已采集量測數據進行比較。若與任意時段相比,量測值變化量百分比均值γ＜0.01%,則進行步驟5,否則轉步驟7。

步驟5：計算當前時段最新外網量測與歷史數據的馬氏距離,選擇馬氏距離小于下側四分位數的歷史時段,得到集合ψ。

步驟6：計算當前時段內網導納與集合ψ內歷史時段內網導納的馬氏距離,采集馬氏距離最小的歷史時段邊界節點量測值,返回步驟4。

步驟7：初始化在線等值網絡等值參數Ei和σi為1（標幺值）和0,線路參數Gi、Bi、Gij、Bij為其上下限的中間值。

步驟8：按式（5）構建相應的等值網絡參數優化模型,采用內點法進行求解,即可獲得等值網絡的參數xi,yij(i=1,2,…,n；j=i+1,i+2,…,n；i≠j)。

上述求解過程主要分為2 個階段：第1 階段是采集量測數據,并保證各時段量測數據能夠穩定求解在線等值網絡參數；第2 階段是根據多時段量測數據,采用式（5）所示模型估計等值網絡參數。程序流程圖如圖3 所示。

3 算例分析

本文以IEEE 39 和118 節點系統為算例,以驗證本文模型和方法的有效性。以額定負荷下的（1±20%）作為外網最大、最小典型運行方式。所有參數及計算結果均以標幺值形式表示。

3.1 量測數據的構造及比較條件

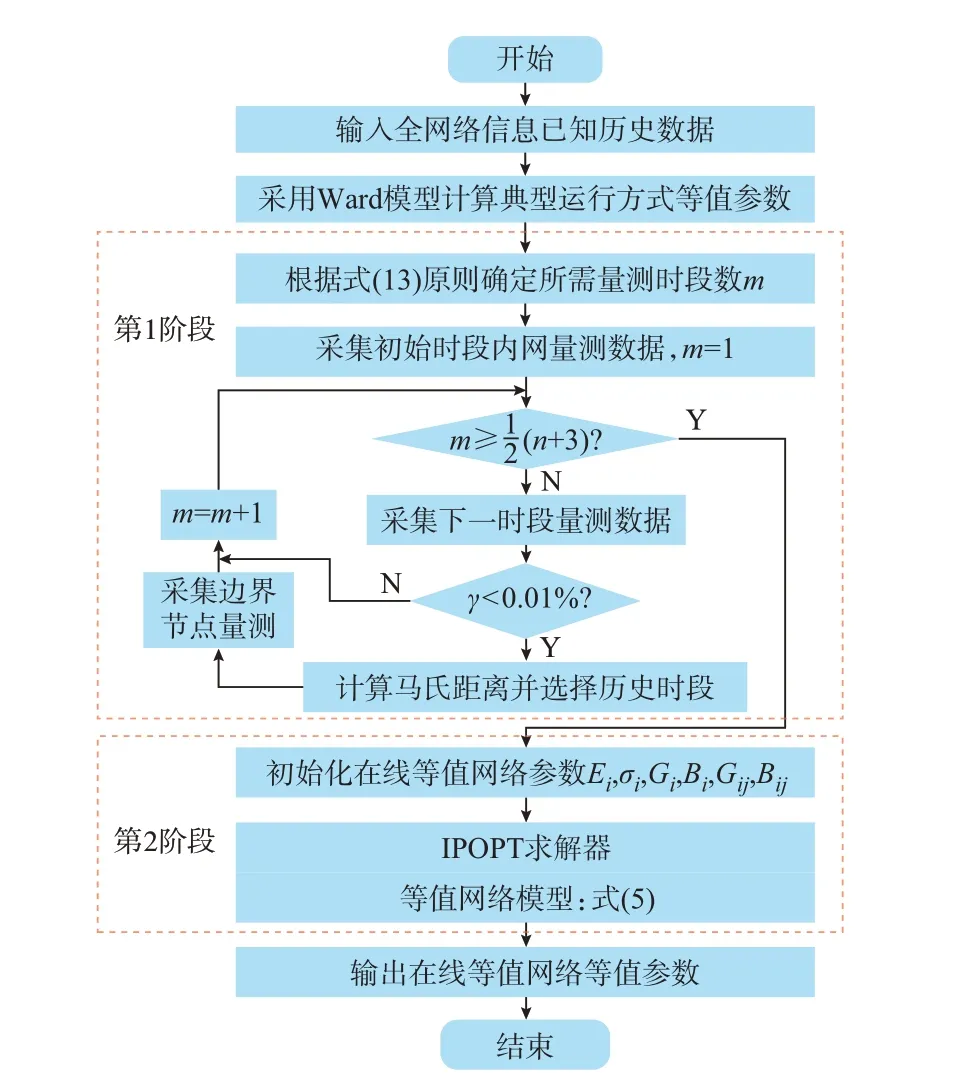
圖3 基于內點法的在線等值網絡等值參數求解流程圖Fig.3 Flow chart of solving equivalent parameters of online equivalent network based on interior point method

假設電網結構不變,各負荷節點功率按典型運行方式下功率的0.01%步長遞增,各發電機有功出力按典型運行方式下功率的0.01%步長遞增,由此可獲得若干個時段的潮流解,用于模擬在線SCADA 量測。

IEEE 39 節點系統中以節點1、3 和17 作為邊界節點,節點2、25～30 和37～39 作為外網節點,其余節點為內網節點,如附錄A 圖A1 所示。3 個邊界節點,根據式（13）原則,需3 個時段的內網量測值,作為等值網絡參數估計的量測數據。IEEE 118 節點系統中以節點15、19、23 和30 作為邊界節點,節點1～14、16～18、20～22、25～29、31、32、113～115、117作為外網節點,其余節點為內網節點。4 個邊界節點,根據式（13）原則,取4 個時段的內網量測值,作為等值網絡參數估計的量測數據。以典型運行方式潮流解為基準狀態,即第1 時段量測數據；基準狀態1 次步長遞增后潮流解作為第2 時段量測數據,依次類推。

通過在負荷節點功率疊加標準差為0.004的30 組高斯白噪聲,來模擬歷史量測數據。IEEE 39 和118 節點系統外網歷史量測數據與當前外網最新時段量測數據的馬氏距離,以及歷史時段內網網絡結構信息與當前內網網絡結構信息之間的馬氏距離分布圖分別如附錄A 圖A2、圖A3 所示。圖中,橫坐標小于四分位數且縱坐標最小的點（即圖中五角星位置）即為外網歷史量測數據與當前最新外網量測數據的馬氏距離小于四分位數且內網歷史網絡結構信息與當前的內網結構信息馬氏距離最小的歷史時段,以該時段邊界節點量測作為補充量測參與等值。

附錄A 表A1 給出了采用本文策略及未采用本文策略進行等值計算的收斂情況對比。可以看出,當系統變化較小時,各時段間量測值變化量小,IEEE 39 和118 節點系統變化量最小值僅為0.001%和0.000 7%,遠小于0.01%,量測變化量均值也分別為0.003%和0.001%,遠小于0.01%,其參數估計時計算不收斂。以附錄A 圖A2、圖A3 中選擇的歷史時段邊界節點量測作為補充量測,各時段間量測值變化量明顯增大,變化量最小值分別達0.017%和0.012%,大于0.01%,平均變化量達到0.021%和0.017%,也明顯大于0.01%,計算結果表明其能有效保證參數估計的收斂性。

3.2 計算結果的對比

在獲得等值網絡參數后,利用等值模型計算內網的潮流分布,并與未等值的全網潮流計算結果進行對比以驗證本文等值模型的精度。由于等值網絡目前大多基于Ward 等值,本文進行Ward 等值對照仿真實驗,以比較驗證本文等值方法的精度。

為了研究量測噪聲對等值結果的影響,在上述基于潮流結果為量測的基礎上分別疊加標準差為σ的高斯白噪聲,電壓幅值、支路功率的量測誤差的標準差均為0.004,以比較量測噪聲對于不同方法計算精度的影響。

采用潮流平均相對誤差和最大誤差2 個等值誤差評價指標,以量度不同方法的等值精度。

潮流平均相對誤差ξave為：

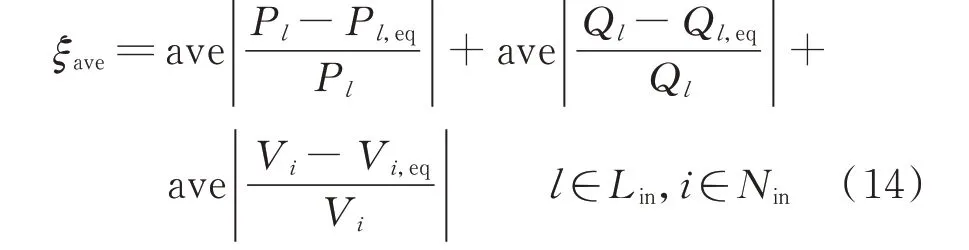
式中：Pl,Pl,eq和Ql,Ql,eq分別為等值前后內網線路l的有功和無功功率值；Vi和Vi,eq分別為等值前后內網節點i的電壓幅值；Lin為內網所有線路集合；Nin為內網所有節點集合；ave 表示對表達式求均值。

潮流最大相對誤差ξmax為：

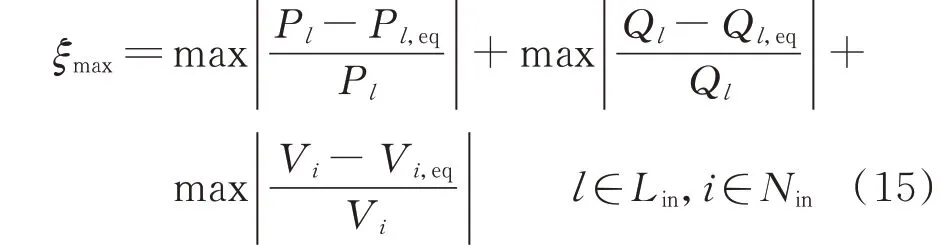
通常情況下,等值網絡并不能精確代表外網,特別是當潮流狀態相對其基本狀態有較大變化時,等值后的網絡潮流誤差較大。為使仿真結果具有代表性,假設在等值過程中電網負荷水平發生了變化。當負荷水平變化為0%時,潮流狀態相對基本狀態保持不變。在線等值采用實時量測數據進行等值,時間跨度不大,通常在5 min 以內。該時間段內,除特殊情況外,負荷水平變化一般不超過1%,因此選擇負荷水平分別變化0%、1%、3%時的潮流誤差來驗證本文等值方法的有效性。

在沒有量測噪聲的情況下,不同負荷水平下的等值模型潮流平均相對誤差和最大誤差分別如附錄A 表A2 和 表A3 所 示。

可以看出,當全網狀態不發生改變時,基于初始狀態全網數據進行Ward 等值所得的模型誤差最小；當負荷水平發生變化時,Ward 模型的誤差遠大于本文等值模型。這是因為Ward 等值是根據初始負荷水平下的潮流狀態進行等值的,其等值結果能夠準確代表電網狀態不發生任何改變時的外網。當電網狀態發生變化如負荷水平增加3%時,基于初始狀態潮流的Ward 等值結果不能準確代表外網,甚至因為等值網絡的誤差,加大了此時內網的潮流誤差,造成內網潮流平均相對誤差和最大誤差2 個指標明顯增大。這說明本文等值模型更適應于潮流狀態變化的實際情況。

附錄A 表A4 和表A5 給出了內網量測具有量測誤差時,Ward 等值模型和在線等值模型的等值誤差。

對比附錄A 表A2、表A4 和表A3、表A5 可以看出,Ward 等值受量測誤差影響更大,本文等值模型雖然在量測誤差的影響下潮流誤差相對于無量測誤差時會有所增大,但電網狀態變化不大時仍能保持較高的精度,負荷水平變化低于1%時潮流平均誤差嚴格控制在1%以內。

當外網拓撲結構發生變化時,存在3 種可能：①該變化發生在內網量測數據采集之前,內網量測數據包含了該變化對電網的影響；②該變化發生在內網量測數據采集時段,內網量測數據部分包含該變化的影響；③該變化發生在內網量測數據采集之后,內網量測數據不包含該變化的影響。

附錄A 表A6 給出了IEEE 39 節點系統開斷25-26 支路和IEEE 118 節點系統切除80 號節點發電機在3 種可能下的在線等值模型誤差。可以看出,拓撲變化發生在內網量測數據采集前時,等值網絡能準確反映外網狀態；拓撲變化發生在內網量測數據采集時,等值網絡能近似反映外網狀態。雖然內網量測數據采集后外網拓撲發生改變,等值誤差較大,但需注意的是,在線等值是實時進行的,每次等值間隔很短,具體間隔時長取決于量測頻率和運營公司計算資源。現有設備資源確定的等值間隔通常已經能夠保證,當外網拓撲變化發生在可能②或可能③時,下一次等值很快開始,此次等值屬于可能①,能夠滿足運營公司對潮流計算精度的需求。

4 結語

本文提出了基于內網量測數據的外網在線等值新方法。該方法基于邊界節點多個時段的SCADA信息,構建外網等值網絡及相應的參數優化辨識模型。該模型以等值網絡邊界節點的計算值與量測值多時段最為接近為目標函數,以相應的等值參數位于其合理區間為約束,使得等值網絡在邊界節點的計算值既最接近于量測值,又使得其參數位于合理區間內。當時段間的量測差別很小時,本文提出了基于歷史信息的量測補充獲取策略,避免非計劃外支路開斷,提升了方法的工程實用性。算例證明了本文等值模型的有效性。因本文方法模型完善、計算穩定可靠,有望在實際工程中得到應用。

本文得到廣東電網有限責任公司廣州供電局科技項目(GZJKJXM20170034)的資助，謹此致謝！

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。