基于矢量裕度法的風電并網對低頻振蕩模式影響分析

張愛軍，李丹丹，張清波，邢華棟，石 鵬

（1. 內蒙古電力（集團）有限責任公司內蒙古電力科學研究院,內蒙古自治區呼和浩特市010020；2. 浙江大學電氣工程學院,浙江省杭州市310027；3. 國網四川省電力公司電力科學研究院,四川省成都市610041）

0 引言

21 世紀以來,全球經濟快速發展使得人類對能源的需求急劇增長。然而,當今世界能源結構中占主要地位的化石能源面臨能源危機和環境污染等問題。與化石能源相比,可再生能源具有資源豐富、分布廣泛、可再生和清潔環保等優點,成為人們廣泛關注的替代能源。中國風能豐富的儲量為風電的大規模發展提供了可能。在眾多類型的風力發電機中,雙饋感應發電機（doubly-fed induction generator,DFIG）由于勵磁變換器容量小、發電機體積小、成本低等優點被廣泛應用于世界范圍內的風電場中［1］。

內蒙古自治區是國內大型能源送出基地,具有天然的風能資源和區位優勢［2］。但是內蒙古電網地處華北主網的末端,這樣大規模的集中并網以及遠距離外送使得低頻振蕩問題更加突出。

在分析電力系統小干擾問題時,一般認為干擾很小,根據李雅普諾夫線性化理論,可以用線性系統理論加以研究。目前,關于風電并網低頻振蕩問題的分析方法,國內外學者已做了大量研究。其中較為典型的是模式分析法和阻尼轉矩法。模式分析法通過計算風電機組并網前后的特征值、特征向量等分析風電機組對系統阻尼比的影響［3］；而阻尼轉矩法是通過阻尼轉矩的概念,計算風電機組對各臺同步機阻尼轉矩的貢獻程度［4］。此外,文獻［5］提出了一種多頻段電力系統穩定器參數整定的方法。文獻［6］利用發電機控制裝置來定位和識別振蕩源。文獻［7］研究了光伏電站的接入對多機電力系統低頻振蕩的影響。文獻［8］對雙饋風電場并網模型進行了數字仿真。文獻［9］提出一種虛擬阻尼指標用于評估換流站控制對柔性直流電網小干擾穩定性的影響。文獻［10］提出了一種描述雙饋感應發電機并網帶來的動態交互對系統機電模式影響的指標。

現有的方法大多需要計算特征值和左右特征向量,且風電并網對電力系統低頻振蕩的影響仍沒有一般性的結論,因此需要尋找新的分析方法。本文基于矢量裕度法,介紹了一種分析風電并網對低頻振蕩模式影響的方法。首先推導得到由風電機組傳遞函數矩陣和多機同步電網傳遞函數矩陣構成的反饋連接模型,然后介紹矢量裕度法的理論基礎,并將該理論應用于風電機組并網的穩定性分析。在矢量裕度法運用于多臺風電機組并網時,利用多機同步電網傳遞函數矩陣在振蕩頻率處“秩一”的性質,獲得和單臺風力機并網相似的“矢量和”的形式,最終可以通過矢量裕度分量圖直觀地看到不同風力機在振蕩模式下對穩定性的貢獻。最后,將矢量裕度法應用于內蒙古電網算例,并把計算結果和特征值法的計算結果進行對比,驗證了該分析方法的有效性。

1 風電并網電力系統的小信號反饋連接模型

如圖1 所示的DFIG 接入多機同步電網的示意圖中,將系統在風力機的機端母線處分為由風電機組系統與n節點多機同步電網系統構成的反饋連接模型。

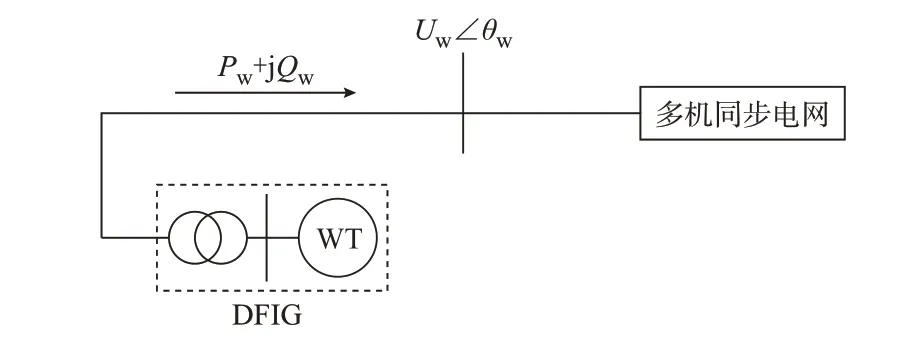
圖1 DFIG 接入的多機同步電網Fig.1 Multi-machine synchronous grid integrated with DFIG

圖1 中,Pw為風電機組的輸出有功功率,Qw為風電機組的輸出無功功率,Uw為風電機組節點電壓幅值,θw為風電機組節點電壓相角。對于雙饋風電機組系統,將機端電壓幅值偏差量ΔUw作為輸入,有功和無功偏差量［ΔPw,ΔQw］T作為輸出,得到雙饋風電機組系統傳遞函數矩陣為［KP（s）,KQ（s）］T。對于多機同步電網系統,將風電饋入電網的有功和無功偏差量［ΔPw,ΔQw］T作為輸入,風電機端母線電壓幅值偏差量ΔUw作為輸出,可以得到多機同步電網傳遞函數矩陣為［GP（s）,GQ（s）］。由此得到風電并網電力系統反饋連接模型如圖2 所示［10-11］。

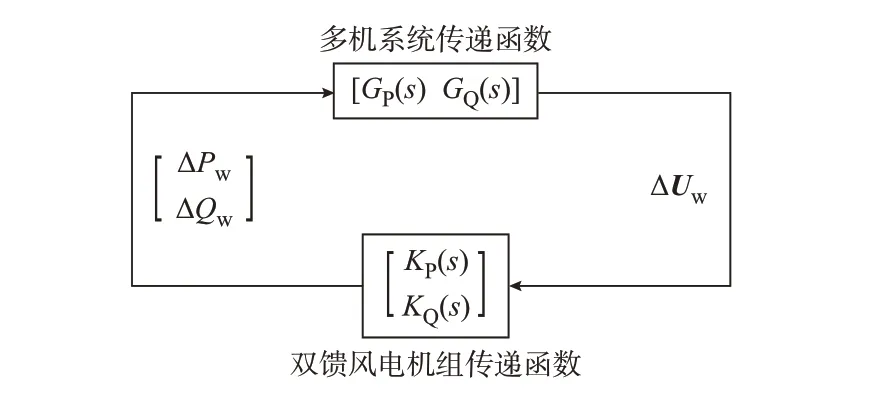
圖2 風電并網電力系統反饋連接模型Fig.2 Feedback connection model of power system integrated with wind power

具體地,將風電機組模型線性化并整理后得到：

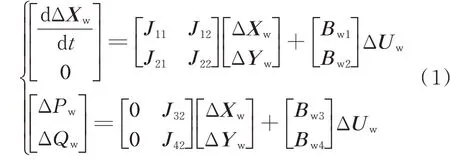
式中：ΔXw為雙饋風電機組系統狀態變量偏差量的向量；ΔYw為雙饋風電機組系統代數變量偏差量的向量；J11,J12,J21,J22,Bw1,Bw2分別為微分代數方程組對ΔXw,ΔYw和ΔUw的偏導系數矩陣；J32,J42,Bw3,Bw4分別為輸出方程對ΔXw,ΔYw和ΔUw的偏導系數矩陣；t表示時間。

引入拉普拉斯變換,對式（1）進行Schur 變換后得到風電機組系統的傳遞函數矩陣［KP（s）,KQ（s）］T的狀態空間描述,如式（2）所示。

式中：I為和Aw相同維度的單位矩陣。

多機同步電網的部分線性化模型為：

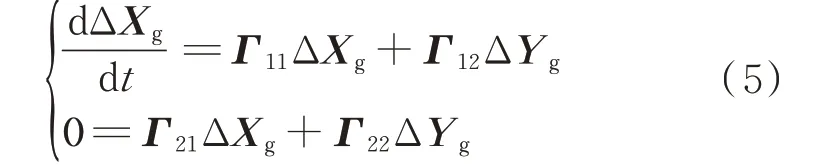
式中：ΔXg=[Δδ,Δω,ΔE'q,ΔEfd]T為多機同步系統狀態變量偏差量的向量,其中Δδ為同步機轉子角的偏差量,Δω為同步機轉子角速度的偏差量,ΔE'q為q軸暫態電勢的偏差量,ΔEfd為勵磁電壓的偏差量；ΔYg=[ΔId,ΔIq,Δθ,ΔU]T為代數變量偏差量的向量,其中ΔId和ΔIq分別為多機同步系統中各臺同步機組定子d軸和q軸繞組電流分量的偏差量,Δθ和ΔU分別為所有節點電壓及相角的偏差量；Γ11,Γ12,Γ21,Γ22分別為微分代數方程組對于ΔXg和ΔYg的偏導系數矩陣。

DFIG 機端母線節點處的系統潮流平衡方程如下：

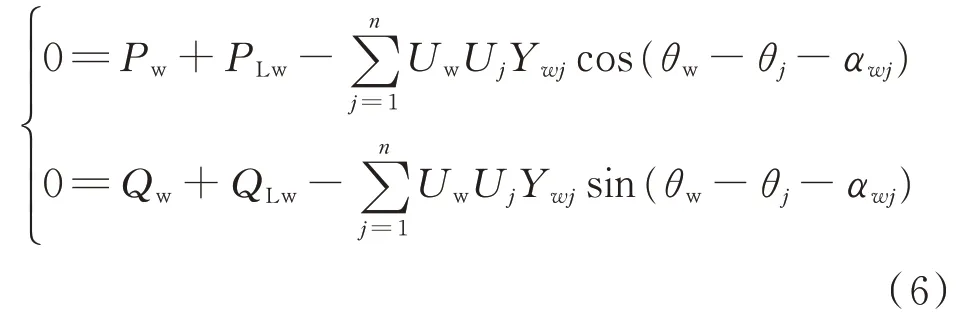
式中：PLw和QLw分別為雙饋風電機組機端母線處恒功率負荷的有功部分和無功部分；θw為風電機組機端母線的電壓相角；θj為網絡中節點j的電壓相角；Uw為風電機組機端母線的電壓幅值；Uj為網絡中節點j的電壓幅值；Ywj為節點w和節點j之間導納的幅值；αwj為節點w和節點j之間導納的相角。

將式（6）線性化可以得到多機同步電網的輸入方程為：

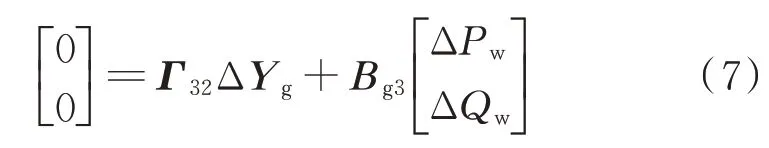
式中：Γ32為式（6）線性化后代數變量的系數矩陣,當系統中同步機組為m臺時,Γ32的維度為2×(2m+2n),此時Bg3=diag（1,1）。

多機同步電網系統的輸出為風電機組機端母線的電壓幅值偏差量ΔUw,而ΔUw是多機同步系統代數變量,因此同步電網的輸出方程為：

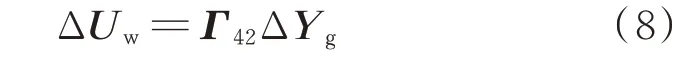
式中：Γ42是維度為1×(2m+2n)的矩陣。

將式（5）、式（7）、式（8）進行聯立并引入拉氏變換后得到：

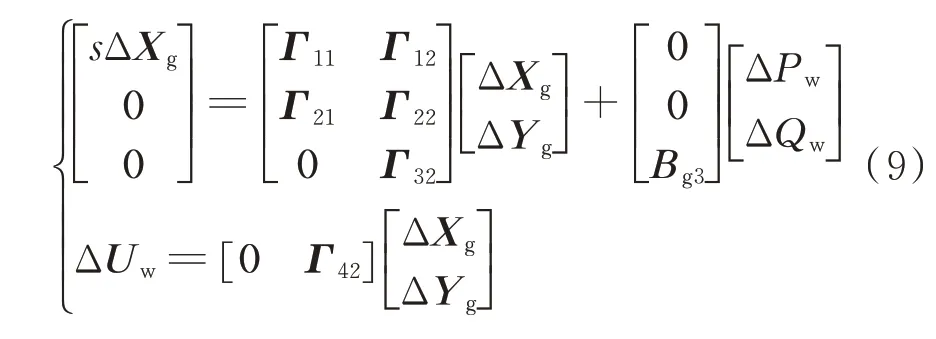
將式（9）進行Schur 變換后可以得到多機同步電網的傳遞函數矩陣［GP（s）,GQ（s）］的狀態空間描述：

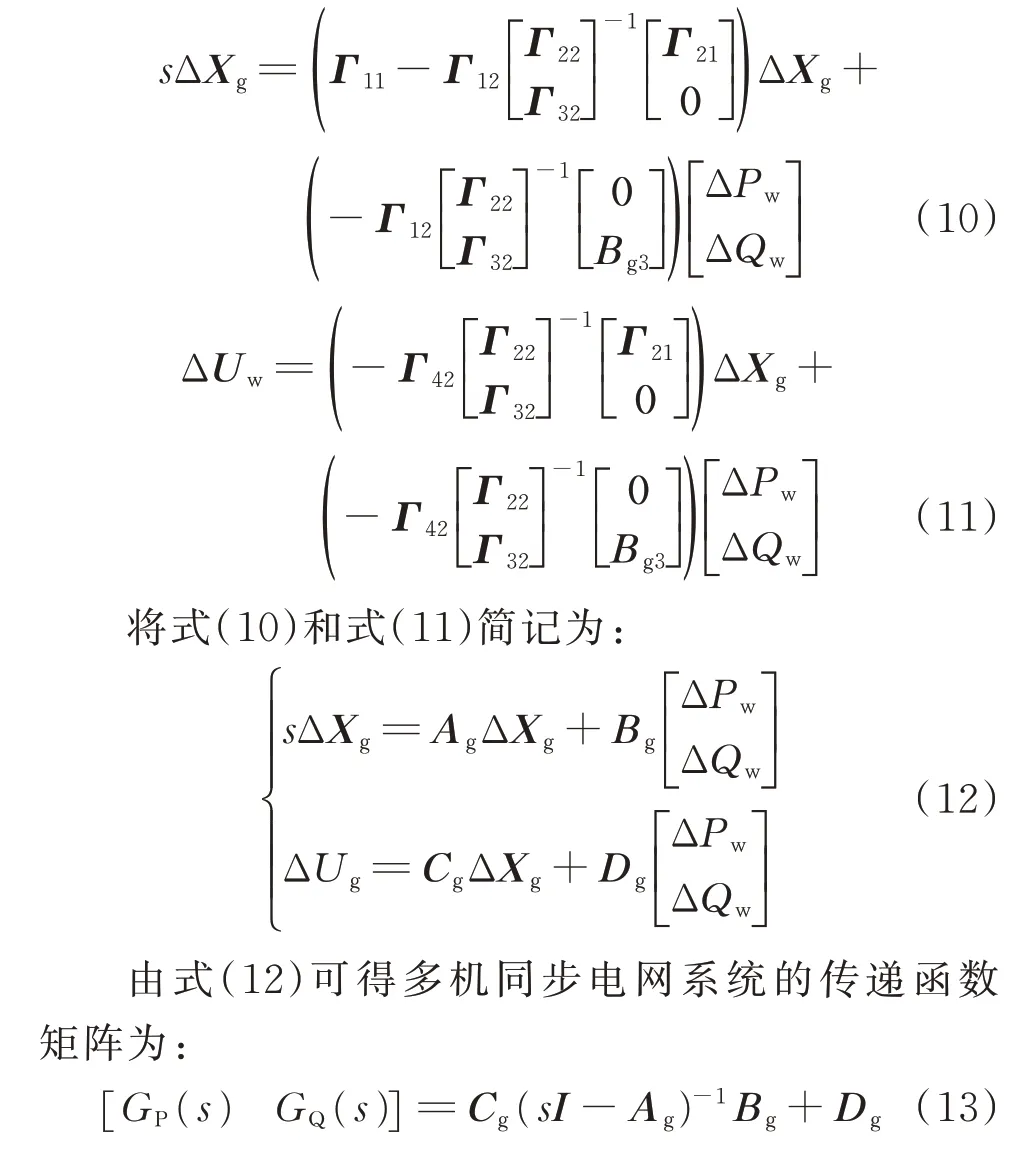
由此推導得到風電并網電力系統的小信號反饋連接模型。關于偏差量的大小,文獻上并沒有明確的共識,經驗認為,偏差信號的大小應該小于額定數量的5%。為了彌補這一小信號模型的不足,文獻往往在提出小干擾穩定控制措施的時候,采用非線性仿真來校核,這種處理辦法已經成為共識。

在具體的實施方法上,可以通過BPA 和DIgSILENT 等專業軟件得到系統雅可比矩陣,再根據需要構造風電機組系統以及多機同步電網系統輸入輸出方程,進而得到類似式（1）和式（9）的形式,然后通過常用的數學工具如MATLAB 等進行Schur 變換就可以得到風電機組系統矩陣Aw,Bw,Cw,Dw以及多機同步電網系統矩陣Ag,Bg,Cg,Dg。

DFIG 在實際運行中的控制方式通常是機端電壓相角定向,并且鎖相環的動態特性在低頻振蕩問題分析中可以忽略［4,10-12］,即認為機端電壓相位變化不會導致風電機組輸出信號的變化,因此風電機組機端電壓相位信號在這里不再考慮。

2 基于矢量裕度法的穩定性分析方法

2.1 矢量裕度法

系統的奈奎斯特曲線L（jω）（或廣義奈奎斯特曲線）距離（-1,0）點的最小距離|VM|決定了系統的穩定裕度［13-14］,θ為向量VM與實軸的夾角,如圖3 所示,定義|VM|為矢量裕度［15］。

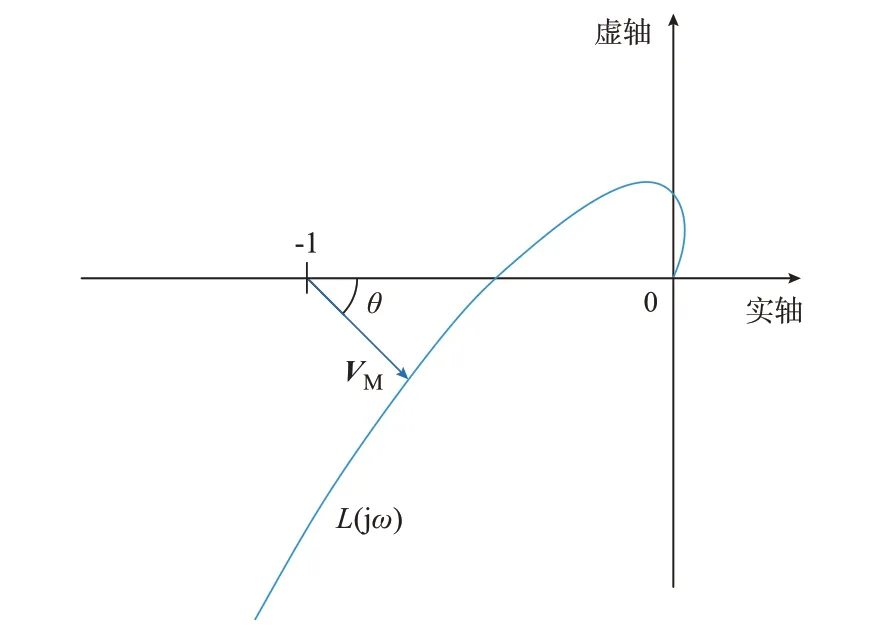
圖3 矢量裕度Fig.3 Vector margin

假設奈奎斯特曲線距離（-1,0）點最近的點對應的掃頻頻率為ω,如果L（jω）可以表示為如下矢量裕度分量相加的數學形式：

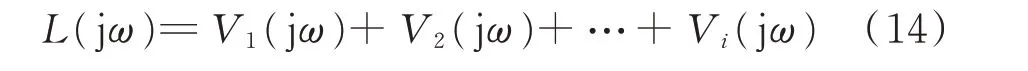
則可以通過觀察式（14）中各個矢量裕度分量Vi（jω）在復平面的位置來判斷各個分量對穩定裕度的影響。如果分量Vi（jω）位于復平面中的相位區間（-π/2-θ,π/2-θ）內,那么Vi（jω）使L（jω）遠離（-1,0）點,穩定裕度增大,因此將(-π/2-θ,π/2-θ)定義為正作用區域；而如果分量Vi（jω）位于復平面中相位區間（π/2-θ,3π/2-θ）內,那么Vi（jω）使L（jω）靠近（-1,0）點,穩定裕度減小,因此將（π/2-θ,3π/2-θ）定義為負作用區域［15］。

2.2 穩定性分析的簡化分析判據

奈奎斯特曲線是ω從0 到正無窮時,開環傳遞函數在復平面上的軌跡。奈奎斯特曲線距離（-1,0）點最近的點對應的頻率在風電機組接入系統后低頻振蕩頻率附近,而通常情況下,風電機組接入前后的低頻振蕩頻率變化不太大。因此,可以將風電機組接入前系統的弱阻尼振蕩模式（λ0=δ0+jω0且ω0?δ0,δ0表示振蕩模式的實部,ω0表示振蕩模式的虛部）對應的振蕩頻率ω0作為距離（-1,0）點最近點的頻率。由此,可以通過觀察L（jω0）的矢量分量的位置判斷各分量對應的機組對低頻振蕩的作用。經驗證明,L（jω0）的矢量分量的計算結果與距離（-1,0）點最近處頻率的L（jω）矢量裕度分量的分析結果相一致。

以上分析主要針對傳統的Hurwitz 穩定性問題,但在電力系統小干擾穩定性分析中常有阻尼比約束條件,此時就從Hurwitz 穩定性問題轉化為D穩定性問題。上述簡化判據同樣可以應用于分析D穩定性問題,如附錄A 所示。此時只需用廣義頻率sg進行計算,即L(sg)。將sg代入式（4）和式（13）中即可得到廣義頻率響應矩陣。后文中將統一以sg進行說明。

除此之外,計算經驗表明θ通常比較小,因此在實際應用中可以忽略。所以在復平面中,正作用區域由(-π/2-θ,π/2-θ)近似為(-π/2,π/2),負作用 區 域 則 由 (π/2-θ,3π/2-θ) 近 似 為(π/2,3π/2)。據此,可以得到簡化后的穩定性分析判據如下：若回路傳遞函數的頻率響應L(sg0)的分量位于區間(-π/2,π/2)內（復平面的一、四象限）,那么該分量使系統穩定裕度增加,故而對系統穩定性起正作用；而若回路傳遞函數的頻率響應L(sg0)的分量位于區間(π/2,3π/2)內（復平面的二、三象限）,那么該分量使系統穩定裕度減小,故而對系統穩定性起負作用。特征值阻尼比變化方向和簡化分析判據的近似一致性的證明在附錄B 中給出,可以發現,矢量分量實部絕對值越大,則對阻尼影響程度越大。因此,可以根據阻尼比的約束條件,靈活選擇對阻尼比影響不同的機組開展穩定控制等防治措施。

2.3 單臺風電機組并網的矢量裕度法分析

由圖2 所示的反饋連接模型可以得到單臺風電機組并網電力系統回路傳遞函數頻率響應為：

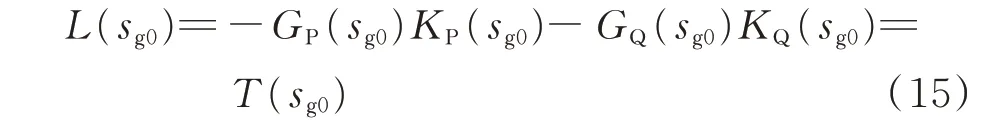
式中：GP(sg0),GQ(sg0)和KP(sg0),KQ(sg0)分別為振蕩頻率為sg0時,多機同步電網的傳遞函數矩陣以及雙饋風電機組系統的傳遞函數矩陣中的元素；T(sg0)為單臺風電機組對穩定性的影響。

由式（15）可知,單臺風電機組并網奈奎斯特曲線在振蕩頻率處具有矢量和的形式,因此可以直接觀察矢量位置對穩定性進行分析。

2.4 多臺風電機組并網的矢量裕度法分析

多臺風電機組同時接入多機同步電網時,其反饋連接模型如圖4 所示是一個多輸入多輸出系統,回路傳遞函數轉變為回差矩陣行列式如式（20）所示。相應地,奈奎斯特曲線轉變為廣義奈奎斯特曲線,即回差矩陣行列式的掃頻曲線。

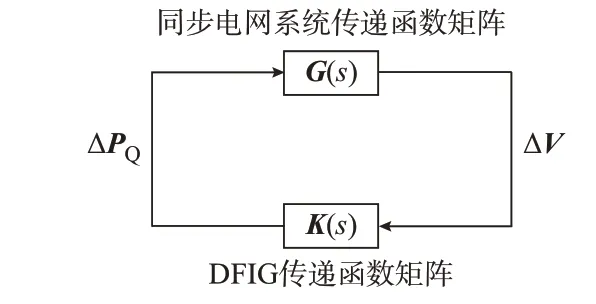
圖4 多臺DFIG 并網反饋連接模型Fig.4 Feedback connection model of multiple gridconnected DFIGs

圖4 中,同步電網系統傳遞函數矩陣G（s）、DFIG 傳遞函數矩陣K（s）、各風電機組有功無功出力偏差ΔPQ以及風電機組節點電壓幅值偏差ΔV的形式和維度分別如下所示：

式（16）和式（17）中各變量為G（s）和K（s）中的元素；式（20）中P（s）為多輸入多輸出系統的回差矩陣行列式,其中M（s）為G（s）和K（s）的乘積。

式（20）中的回差矩陣行列式不具備分量和的函數形式,具體公式見附錄C 式（C1）,但是利用同步電網系統傳遞函數矩陣在低頻振蕩模式附近的sg0處的廣義頻率響應G(sg0)近似“秩一”的性質,再結合Sylvester 不等式［16］能夠證明矩陣M(sg0)的秩近似為1。在此基礎上,利用M(sg0)近似“秩一”的性質和矩陣的對角展開公式［17］簡化det(IM(sg0))得到式（21）。具體的證明推導過程見附錄C。

式中：Ti(sg0)為表示第i臺風電機組在振蕩頻率為sg0時sg0對系統穩定性影響的矢量分量。

由式（21）可知,風電機組之間的相互作用對應的項由于數值較小,可以忽略不計,各臺DFIG 對穩定性的作用分離成為了解析的矢量裕度分量,不同位置的風電機組對阻尼的影響實現解耦,多風電機組并網電力系統反饋連接模型可以簡化為和單臺風電機組并網模型相似的分量和的形式,M(sg0)矩陣的各對角元素代表了多臺風電機組各自對低頻振蕩的影響。因此,可以根據在復平面繪制出的各臺DFIG 對應的矢量裕度分量的相位信息直觀地判斷各臺DFIG 對于電力系統低頻振蕩的影響。

值得說明的是,風電出力隨外界環境會相應變化,當風電出力隨外界環境變化較小時,分析結果不變；當風電出力變化較大時,會引起系統潮流的變化,此時分析結果也會隨之發生變化。

3 仿真驗證

本章基于中國蒙西+華北電網2019 年風電大發運行方式數據,應用矢量裕度法計算在2019 年冬平風電大發運行方式下任選的14 臺出力為49.5 MW,0 Mvar 的DFIG 同時接入時各臺風電機組對中國蒙西-山東區域振蕩模式的影響,并通過特征值計算驗證了矢量裕度法計算結果的有效性。

算例中選定的14 個風電機組節點名稱及地區如表1 所示。

表1 算例選定的DFIG 節點Table 1 Selected DFIG nodes for case study

首先,用恒功率源替代14 臺風電機組,在保證潮流水平不變的情況下,計算得到風電機組接入前系統的區域振蕩模式為λ0=-0.154 4+j2.809 3,阻尼比為5.495%。根據區域振蕩模式的頻率ω0=2.809 3,選擇阻尼比為5.30% 的廣義頻率sg0=-0.053ω0+jω0。對多機同步電網系統的廣義頻率響應矩陣G(sg0)進行奇異值分解后得到奇異值向量為［142.012 799,0.009 904,0.008 872,0.006 598,0.005 255,0.004 967,0.004 878,0.004 778,0.004 550,0.004 425,0.004 317,0.004 037,0.003 917,0.003 719］,因此可知近似地有G(sg0)的置約等于1。最終得到矢量裕度分量圖如圖5 所示。圖5 中,T1至T14分別為表示14 臺DFIG 對蒙西電網穩定性作用的矢量裕度分量。其具體的數值如表2所示。

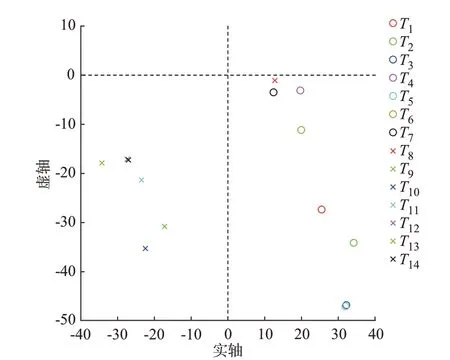
圖5 蒙西電網中14 臺DFIG 作用的矢量裕度分量圖Fig.5 Vector margin component diagram for 14 DFIGs in grid of West Inner Mongolia in China

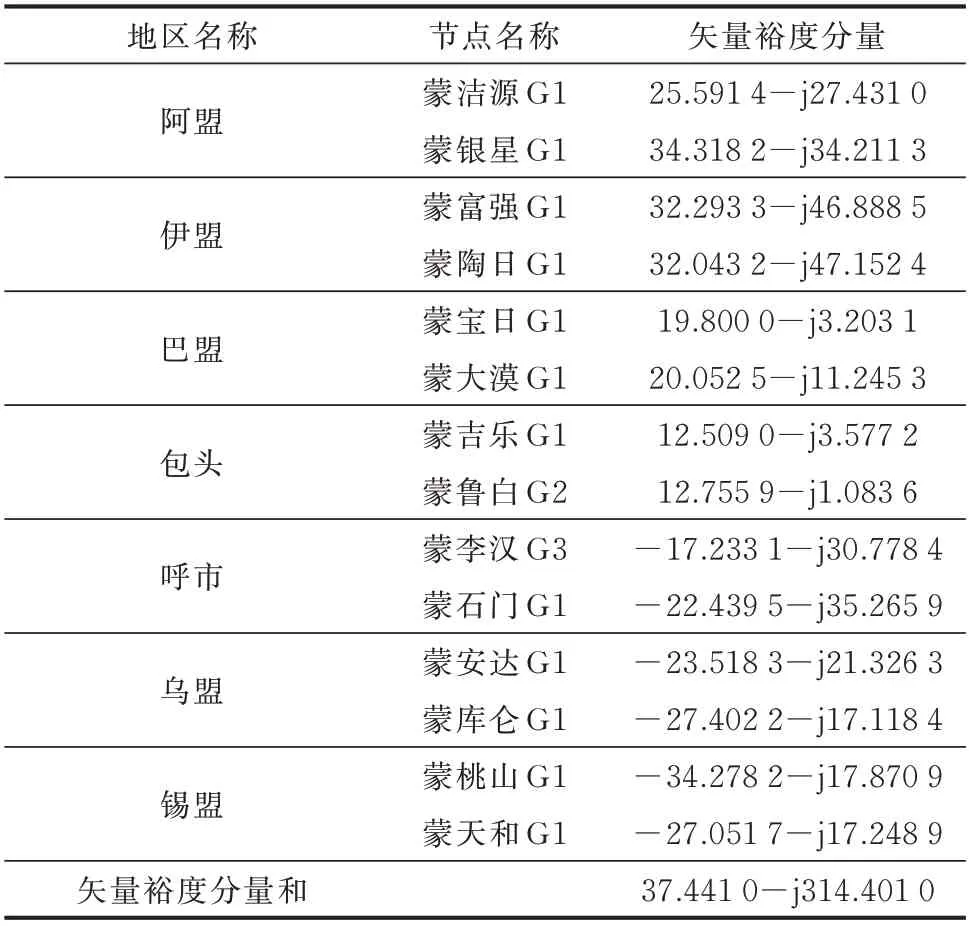
表2 14 臺DFIG 對應的矢量裕度分量Table 2 Vector margin components for 14 DFIGs

由圖5 中各個分量所在的位置可以直觀地看出,T1至T8均位于復平面的右半平面,說明阿盟、伊盟、巴盟以及包頭4 個地區的8 臺DFIG 均對電網穩定性起正作用；而T9至T14均位于復平面的左半平面,說明呼市、烏盟和錫盟地區的6 臺DFIG 對電網穩定性起負作用,且各臺機組對穩定性的作用程度隨著矢量裕度分量到虛軸距離的增大而增大。另外如附錄D 所示,結合蒙西各個地區的地理位置還可以看出,同一地區的DFIG 對系統穩定性的作用較為接近,相鄰地區的DFIG 對系統穩定性的作用較為接近,靠西側地區的風電機組接入對系統穩定性起正作用,靠近東側的則正好相反,且越靠近兩端的風電機組對系統穩定性影響越大。這進一步體現出,在模型和出力均相同時,DFIG 對系統穩定性的影響主要取決于其接入的位置。將T1至T14相加可以發現,這14 臺DFIG 同時接入電網時,矢量裕度和在右半平面,說明14 臺DFIG 同時接入后,雖然部分起正作用,部分起負作用,但是因為起正作用的程度大于起負作用的程度,因此最終是提高了系統的穩定性。

以上結論可以通過特征值計算進行驗證。具體地,將14 臺DFIG 全部接入系統中計算閉環系統區域振蕩模式。再分別將阿盟—烏盟的DFIG 替換為恒功率源計算特征值,以印證各地區DFIG 對系統穩定性的影響。具體的計算結果如表3 所示。

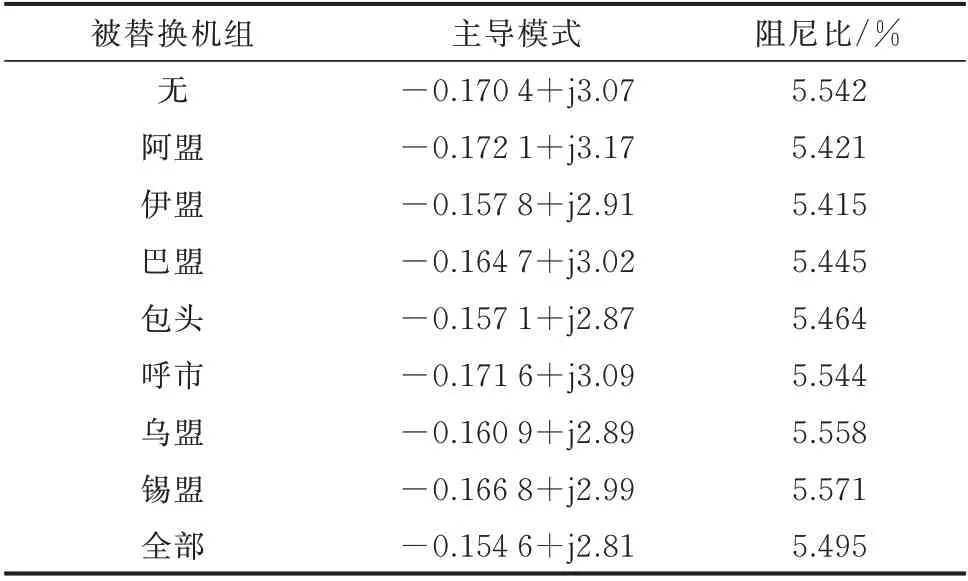
表3 算例特征值結果Table 3 Eigenvalue results of case study

從表3 中可以看出,將阿盟、伊盟、巴盟以及包頭的8 臺DFIG 替換,振蕩模式阻尼較14 臺DFIG 同時接入時小,而替換呼市、錫盟和烏盟的6 臺DFIG,其結果剛好相反。算例結果說明,基于矢量裕度法的風電并網對低頻振蕩模式影響的分析方法具有可行性。

在實際的電力系統當中,可以計算不同的運行方式下所關注的風電機組對于振蕩模式的影響,根據計算結果選擇是否接入風電或者選擇起負作用較大的機組增加相應的穩定控制等防治措施,從而達到靈活調節穩定裕度的目的,也為方式調節提供了參考,對實際電網運行具有指導意義。

4 結語

本文提出了一種基于矢量裕度法的風電并網電力系統低頻振蕩問題的分析方法。該方法可以計算多臺DFIG 同時接入電網時,各自對系統低頻振蕩模式的影響,并通過二維復平面圖示化的方法使得分析結果更加清晰直觀。該方法不需要傳統分析方法中所依賴的特征值、特征向量等的計算,具有處理過程簡單,分析結果直觀的特點。分析結果表明,多機同步電網和風電機組系統頻率響應矩陣的部分元素的相位之和決定了不同風電機組對系統穩定性的影響。蒙西電網算例結果驗證了該方法的有效性,為低頻振蕩的防治提供了技術手段。然而,當系統運行方式改變時,各臺風電機組對系統穩定性的影響如何隨運行方式改變而改變還是一個難題,需要更進一步的研究。

本文受到內蒙古電力集團（有限）責任公司科技項目（發文號：內電科信〔2019〕6 號）資助，特此感謝！

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。