含電動汽車集群調頻的信息能源系統譜特征和穩定性評估

張一媚，董朝宇，董曉紅，肖 遷，張明東，賈宏杰

（1. 智能電網教育部重點實驗室（天津大學）,天津市300072；2. 河北工業大學人工智能與數據科學學院,天津市300130；3. 天津大學智能與計算學部,天津市300072）

0 引言

隨著環境污染加劇和化石資源逐漸枯竭以及間歇性可再生能源的大規模利用,經聚合后形成的電動汽車（electric vehicle,EV）集群,憑借快速的功率輸出與響應特性,成為一種很好的調控資源,可用于平滑可再生能源出力、提供輔助服務等領域［1-5］。利用EV 集群提供調頻服務已成為近期的一個研究熱點。

EV 集群參與調頻時,首先需收集和發送EV 狀態到控制中心,然后根據控制信號,對集群內EV 充放電行為實施控制［6］,這一過程涉及對大量EV 的信息收集和協調控制。毫無疑問,此時的電力系統成為一個典型的信息能源系統,即信息與能源技術深度融合并集成能源網、通信和計算的復雜系統［7-11］,評估其穩定性需要同時考慮能量流和信息流的影響。在對大量分散EV 進行調控時,出于經濟性考慮,應用異構通信手段甚至直接借助公共通信媒介成為必然選擇,由此導致信息傳輸環節的數據擁塞、丟包、延時等情況必然時有發生。在數學模型中可用時滯對其統一加以刻畫［12］。而時滯往往會影響系統動態性能甚至引發失穩［13-16］。頻率小擾動穩定過程既可能是秒級的短期現象［17］,也可能是從幾十秒到幾分鐘的長期現象［18-20］。研究EV 集群參與系統調頻時,需借助時滯穩定性分析方法來科學評估時滯的影響［21-26］。

時滯穩定性分析方法包含時域法和頻域法［16］：時域法通過對Lyapunov 泛函進行放縮得到充分不必要條件,盡管可以通過等效變換［21］、新泛函構造［22-23］及優化判據推導［24］等手段對其加以改進,但依然無法消除保守性；而頻域法的基礎是頻域變換技術和特征值理論,盡管沒有保守性,但時滯引入難以處理的超越項［16］。在文獻［26］中,利用指數延遲項的Pade 有理多項式逼近,避免了直接求解時滯特征方程的困難,但難以應用于時滯較大或規模較大的系統中。文獻［15］采用解算子離散化方案求解系統關鍵特征值,但是存在時滯研究范圍較小的局限性。

為分析時滯對EV 聚合調控效果的影響,本文將基于頻域法,推導一種信息能源系統譜特征和穩定性評估方法。首先,建立EV 集群調頻的系統模型。進一步,將含物理-信息環節的系統譜轉換成無窮小算子的譜,消除超越項；然后,基于用戶準確度與速度需求選擇離散化方案,利用切比雪夫離散化生成有限維近似矩陣,進而利用牛頓迭代校正近似矩陣的特征值,得到系統準確特征值；最后,刻畫系統穩定域,可多角度評估時滯對系統穩定性的影響。提出的方法解決了時域法存在保守性的問題,也消除了頻域法中難以處理的超越項,通過將譜變換、譜離散、牛頓迭代等關鍵技術與用戶需求相結合,可以實現高效準確評估規模或時滯較大系統。

1 系統模型

1.1 EV 集群動態特性

考慮大量EV 集群行為時,一般可用EV 集群來表示。假設系統中存在k個EV 集群,即

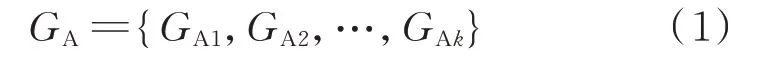
式中：GA為EV 集群構成的集合；GAi為第i個EV 集群；i=1,2,…,k。

對于任意用于頻率調節研究的EV 集群GAi,其中的EV 模型由電池模型和電池充電器模型（包括DC/AC 逆變器）組成。電池充電器控制交流電氣系統和電池之間的電力交換,電池儲存驅動EV 所需的能量。本文采用基于戴維南的模型作為電池的等效電路模型［27-28］。

為簡化分析,忽略了EV 集群中EV 的個體差異。因此,在分析時,假設集群內EV 的荷電狀態（SOC）為常數,認為集群具有等效集群電池系統增益KEVA,i,且集群內EV 的時間常數相同,表示為TEVA,i。可用如下一階慣性環節表示EV 集群的動態特性［29-32］：

式中：GEVA,i和KEVA,i分別為集群GAi的動態特性函數和增益；TEVA,i=Lc/Rc為EV 集群電池系統時間常數,即EV 充電器的時間常數,其中Lc為電池充電器中與電網相連的濾波電抗器,其阻抗通常設計為系統總阻抗的5%,電阻Rc為電抗器電阻及逆變器損耗,取決于電纜尺寸、安裝媒介及導體材料［4,33］。

KEVA,i由頻率調節效果和電池SOC 約束之間的相互限制來決定,以表示EV 輸出功率對頻率偏差的敏感性,其數值主要取決于集群內EV 數量、EV電池的開路電壓、單個EV 采用的控制策略及控制增益最大值［3,28,34］。而控制增益最大值可由EV 入網（V2G）最大功率（或電流）對系統允許頻率偏差的敏感度計算［35］。綜合考慮上述因素,可以對EV調頻等值模型中的參數KEVA,i和TEVA,i進行確定。

需要指出的是,式（2）模型主要用于模擬EV 集群在參與調頻時的總體動態特征,它忽略了EV 個體之間的細微差異,在EV 數量較大時,這一處理誤差較小［36］。

1.2 考慮時滯時的調頻模型

多個EV 集群參與系統調頻的實現原理如圖1所示。當EV 接入電網時,可通過充放電裝置并利用V2G 技術,實現EV 與電網間能量和信息的雙向流動。因EV 單體功率較小,大量分散接入電網后,需引入EV 集成商來負責EV 的充放電管理,以及與上級調度中心的交互。圖1 中的每一個集成商負責監視、收集、分析和計算EV 集群的調控能力,然后上傳至調度中心,同時負責執行調度中心下達的控制指令。

圖1 EV 集群參與調頻的信息能源系統控制框架Fig.1 Framework of frequency regulation for cyber-energy system with EV cluster

信息在EV 和調度中心之間的雙向傳輸過程中必然存在一定時滯。為簡單起見,假設每個EV 集群內所有的EV 擁有相同數據傳輸時滯,則由時滯構成的集合如下：

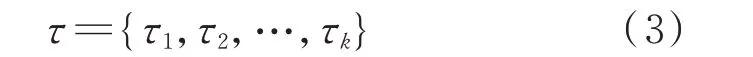
式中：τi為集群GAi的時滯。

本文在研究EV 集群參與系統調頻時,將采用文獻［6］的多區域電力系統模型。任何一個區域w的情況如圖2 所示（假設系統中共包含g個如圖2 所示區域）,它包含一個等效發電單元和多個EV 集群。發電單元包含調速器和再熱式渦輪機,EV 集群考慮了信息傳輸時滯,它們通過參與因子α0,α1,…,αk實現功率分擔。不同區域間通過區域控制誤差（area control error,ACE）實現有機協調［6］。

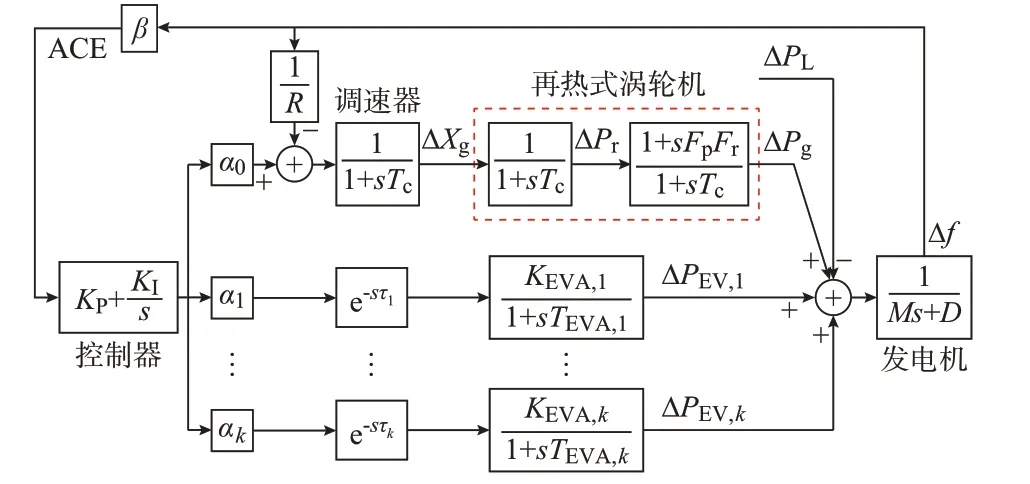
圖2 包括多個EV 集群的電力系統調頻模型Fig.2 Frequency regulation model of power system with multiple EV clusters

單個區域的狀態空間方程為［37-38］：

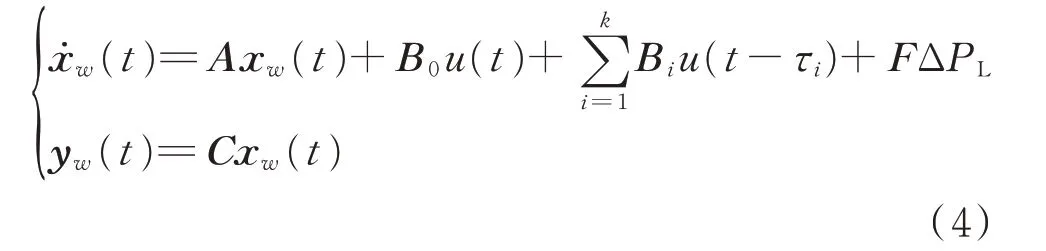
式中：xw,u,yw分別為系統的狀態、控制、輸出變量；A,B0,Bi,F,C分別為狀態矩陣、非時滯控制矩陣、時滯控制矩陣、擾動矩陣、輸出矩陣；ΔPL為負荷偏差。式（4）的詳細推導及各矩陣組成見附錄A。

經簡單變換,式（4）可表述為時滯微分方程：

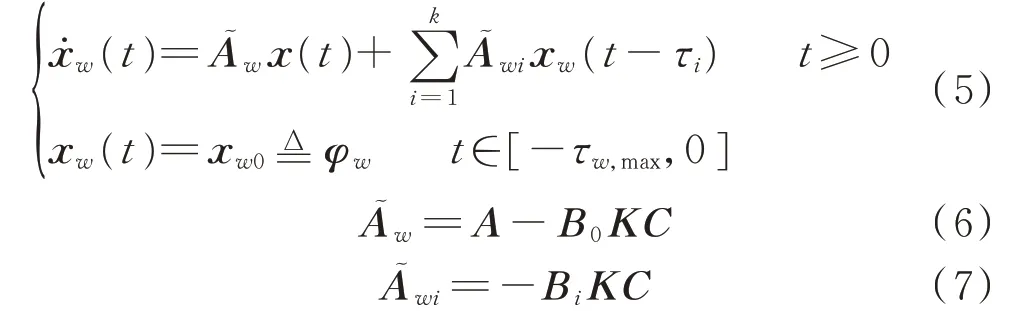
式 中：φw( =xw0)為 區 域w的 初 始 狀 態；τw,max=max {τi},其中i=1,2,…,k；K=［KP,KI］,其中KP和KI分別為區域w中比例-積分（PI）控制器的比例增益和積分增益。

需要指出的是,當系統存在g（g＞1）個區域時,每一個區域內的系統方程均可通過上述過程推導。最后,再將各區域方程進一步整合,得到整個系統的動態方程［6］,即

其中

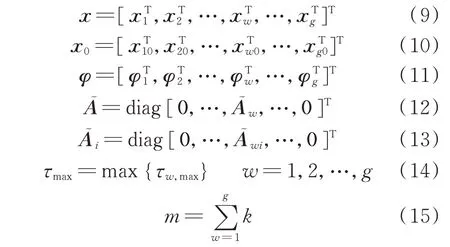
式中：x為系統的狀態；φ為系統的初始狀態；x0為系統初始狀態。

進而可以得到系統的特征方程為：

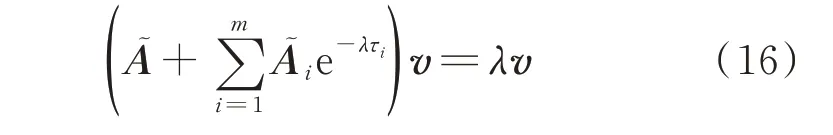
式中：λ為特征值；υ為對應特征向量。

2 基于譜特征提取的穩定域求解方法

由式（8）和式（16）可知,系統的漸進穩定性將由φ、系數矩陣A?和A?i（i=1,2,…,m）以及信息環節時滯τ1,τ2,…,τm唯一決定。理論上,上述參數給定后,時滯系統穩定運行區域（穩定域）可唯一確定,而穩定域可用于多角度評估系統穩定性。本章將推導一種穩定域求解方法,其中間過程的一些結果還有助于分析系統關鍵特征值信息。其主要步驟如下。

1）譜變換：利用無窮小算子,將反映信息能源系統模型動態的時滯微分方程映射為常微分方程,從而消除難以處理的超越項。

2）切比雪夫離散化：對譜變換得到的無窮小算子進行切比雪夫離散化,得到近似離散化矩陣,將無窮維特征值問題轉化為有限維特征值問題。

3）牛頓迭代校正：計算離散化矩陣的特征值及特征向量,將其作為牛頓法初值進行迭代校正,得到系統準確特征值。

4）穩定域求解：基于用戶需求,快速推導出信息能源系統的臨界特征值,進而通過搜索法求解系統穩定域,多角度評估系統穩定性。

2.1 譜變換

對于式（8）系統,令X：=C([-τmax,0],Cn)為由將區間[-τmax,0]映射到n維復數向量空間Cn的連續函數構成的巴拿赫空間。因為式（8）在［0,∞）內連續,假設初始狀態φ存在于巴拿赫空間上,系統x（t）軌跡將在時域內連續且唯一,因此可將式（8）重新表述為巴拿赫空間X上的抽象常微分方程［39］：

式中：H：D(Hφ)?X→X是由式（18）定義的無窮小算子。

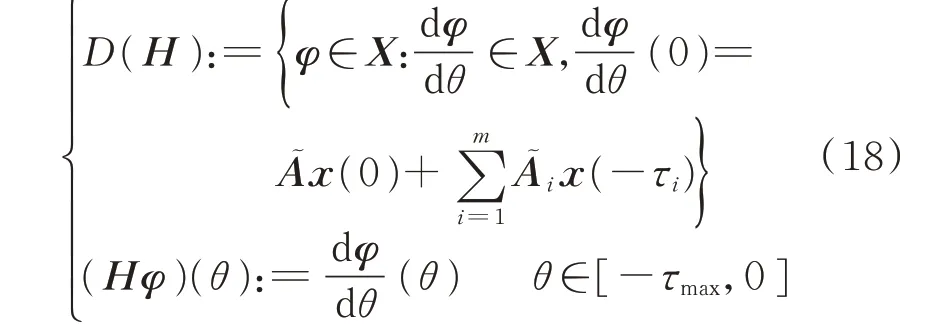
利用上式將t處系統狀態映射到t+θ處,根據譜映射原理,原系統特征值將等于H的特征值［40］。

2.2 切比雪夫離散化

譜變換后得到的式（17）仍為無窮維系統,為簡化求解,利用切比雪夫多項式插值近似初始函數,從而構造離散矩陣來逼近H。

首先,給定正整數N,考慮由N+1 個在區間[-τmax,0]內的離散點組成的網格ΩN：

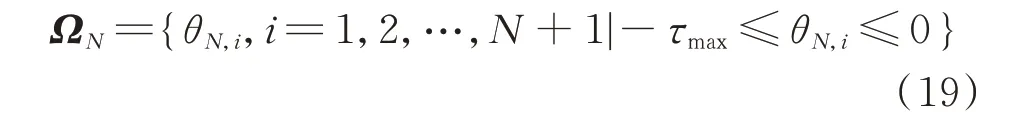
離散化矩陣HN的詳細推導及表達形式如附錄B 所示。

經上述處理后,無限維的H被簡化成有限維的HN。進而可直接求解系統的一組臨界特征值,而不必求解其全部（無窮多）特征值。

2.3 牛頓迭代

在計算得到系統臨界特征值的近似結果λ?后（即HN最右側特征值）,將其和對應Krylov 向量的前n個元素v?,一起作為式（16）的初值{λ?,v?},然后利用牛頓法迭代校正,以得到準確值。

首先,將特征方程式（16）寫成如下格式：

式中：In為n階單位矩陣。

在迭代過程中v需要有一些標準化處理,以保證解的唯一性,迭代過程基于式（23）或式（24）。

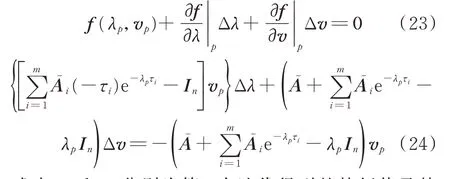
式中：λp和vp分別為第p次迭代得到的特征值及特征向量。

式（24）可寫為如下形式：

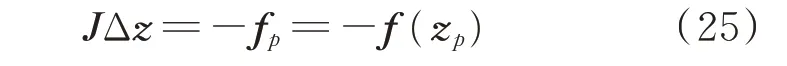
式中：fp為第p次迭代的函數值f；Δz包括Δv的所有元素,其中Δv中的單位元素被替換為Δλ；J為雅可比矩陣。

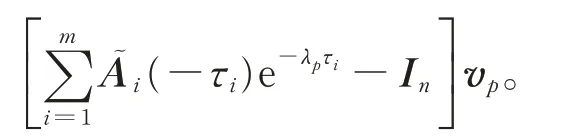
將式（25）轉換為迭代公式,求得第p+1 次的迭代結果為：

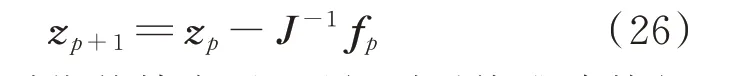
經迭代達到收斂精度后,可得到系統準確特征值和特征向量{λ,v}。

2.4 系統穩定域求解

根據牛頓迭代得到的準確特征值,可以評估系統穩定性,進而可根據用戶需求刻畫穩定域。

通常用戶需求體現在2 個方面：①穩定域準確度；②計算時間。基于此可以對離散化參數N進行選擇,以尋求計算準確度與速度指標的平衡。

利用選擇的特征值計算方法對某一參數下的系統特征值進行求解,進而可以使用成熟的特征值分析方法,對系統穩定性進行分析。

基于此,設置一定的搜索步長,沿時滯增大方向前進,在時滯空間中搜索系統的負實部臨界特征值,直至到達研究區域邊界。可以在不同的控制器參數設置下,對系統的穩定域進行刻畫。

本文提出的譜特征和穩定性評估方法流程如附錄C 圖C1 所示：包括系統初始化和參數輸入、建模、譜變換、切比雪夫離散化、牛頓校正、輸出特征值。而后續進行穩定域刻畫則是在時滯空間中對負實部臨界特征值進行搜索,搜索過程對上述算法進行重復以求解各搜索點特征值。

3 算例分析

以含單個EV 集群調頻的信息能源系統為例,具體參數列在文獻［25］中。基于提出的譜特征提取法對引入通信環節時滯后系統的穩定性進行綜合評估,并將其與以不考慮通信環節時滯的系統為初始狀態的牛頓迭代法及線性矩陣不等式（LMI）方法進行對比算例分析。

為了進一步驗證所提出方法,研究EV 時滯與電力系統調度網絡時滯的區別,在3.3 節設置考慮發電單元引入時滯的信息能源系統,對其穩定域進行刻畫。

3.1 單時滯含EV 調頻的信息能源系統算例

對含單EV 集群的調頻信息能源系統進行分析,其中控制器增益KP設置為0.2,KI設置為0.2,時滯τ設置為100 s,其余系統參數如文獻［25］所示。對此典型算例,利用本文提出方法對系統穩定性進行分析,實現過程如下。

步驟1：系統初始化和參數輸入。以設置N=30 為例,即離散化矩陣維數（N+1）n=186；設置牛頓校正收斂精度為10-6,最大迭代次數為100。

步驟2：建模。基于1.2 節方法對系統進行建模,推導得到系統非時滯參數矩陣和時滯參數矩陣。

步驟3：譜變換。為了避免直接求解含超越項的時滯微分方程,利用無窮小算子將其轉化為抽象常微分方程。這樣,時滯系統的譜轉化為無窮小算子H的譜,進而可以通過計算H的特征值（σ(H)）來獲得原系統的特征值。

步驟4：切比雪夫離散化。基于切比雪夫多項式對H進行離散,得到有限維離散矩陣HN。進而可以計算HN的特征值（σ(HN)）,對H的特征值進行近似求解,如附錄D 圖D1（a）所示。

步驟5：牛頓迭代。由于離散化步驟是近似逼近,因此需要進行校正。以HN的n（n=6）維臨界特征 值 及 特 征 向 量{λ?,v?}為 初 值,應 用 牛 頓 法 求 解式（16）。第p次迭代的J和函數值fp可以由式（24）計算。

步驟6：輸出特征值并進行穩定性分析。得到準確特征值后,可以有效使用特征值分析方法分析當前參數下系統穩定性。在此參數下,臨界特征值實部為0.002 1＞0,意味著系統為負阻尼狀態,會發生增幅振蕩失穩。

步驟7：穩定域求解。基于上述分析過程,可以對研究范圍內其他搜索點進行特征值計算與穩定性分析。設置時滯搜索步長為0.1 s,控制器比例增益步長為0.002,以刻畫在不同的控制器參數下系統的穩定域,如圖3 中紅色區域所示。

3.2 對比算例分析

3.2.1 與以不考慮通信環節時滯的系統為初始狀態的牛頓迭代法比較

為了驗證所提方法的有效性,同時定量分析譜離散化對結果的影響及必要性,設置以不考慮通信環節時滯的系統為初始狀態的牛頓迭代法進行對比分析。

同時,為對離散化維數設置對所提方法影響進行分析,設置不同離散化維數進行對比。

基于上述方法,分別對系統進行穩定性評估,得到了指定系統參數下能獲取準確特征值允許的時滯研究范圍（在本文研究范圍內,采用所提出方法N=200 后再增大離散化維數,特征值結果不變,如附錄E 表E1 所示,因此將該方法得到的特征值,作為驗證方法精確性的基準）。

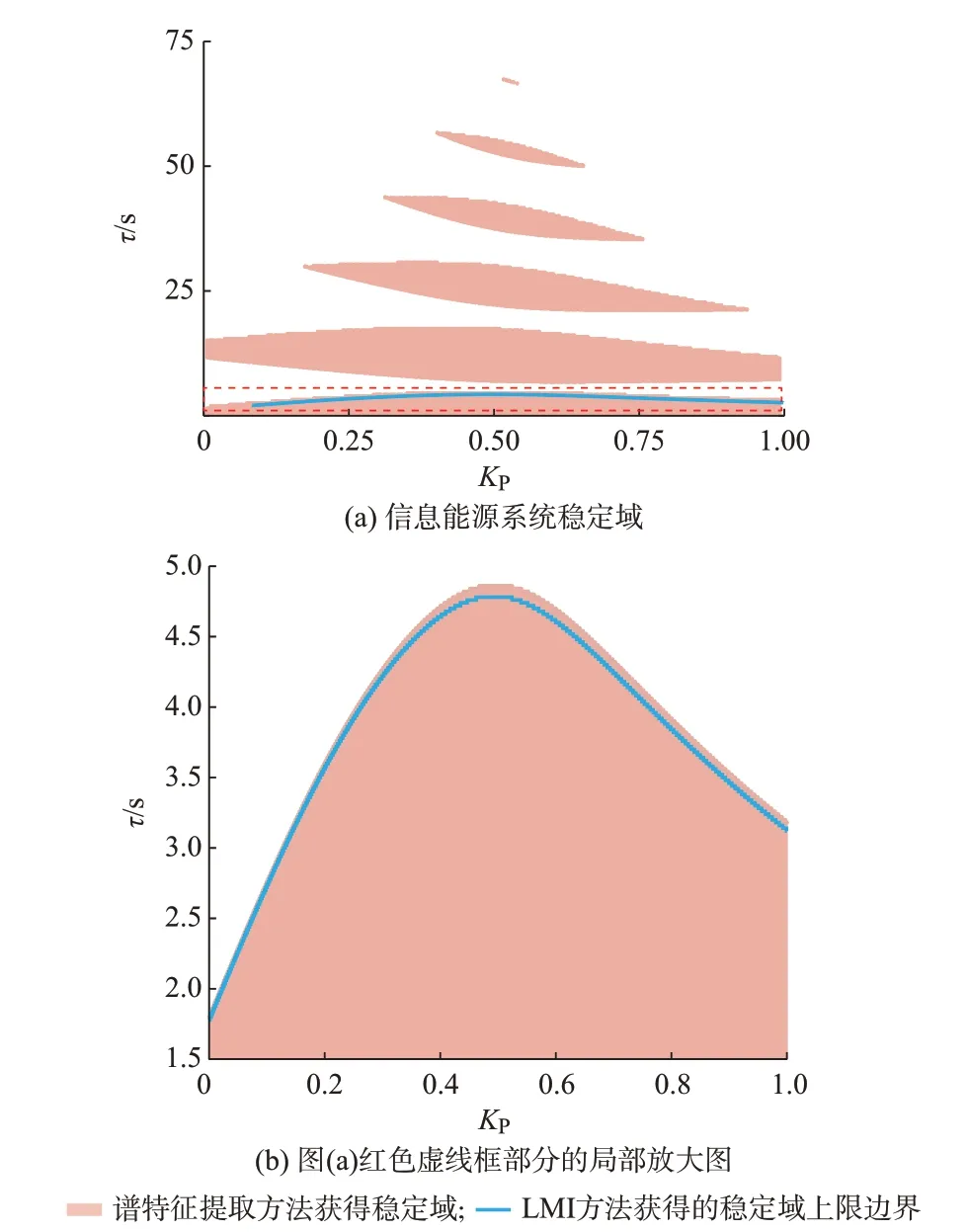
圖3 本文方法與文獻[25]方法結果比較Fig.3 Comparison between the proposed method and that in reference [25]

首先采用以不考慮通信環節時滯的系統為初始狀態的牛頓迭代法,驗證直接進行牛頓迭代的結果,對無時滯的系統(KP=0.2,KI=0.2)求取特征值,將其作為牛頓法初值,經過迭代得到最終值,結果顯示：當時滯τ≤0.5 s 時,可以準確計算系統全部特征值；當0.5 s ＜τ≤36 s 時,不能準確計算全部特征值但仍可準確捕捉臨界（最右側）特征值；而當τ＞36 s時,全部特征值計算不準確。

隨后基于譜特征方法,即對牛頓法初值進行預處理,在相同控制器參數設置下,改變N（N=10,N=20,N=30）,研究全部特征值準確、臨界特征值準確、全部特征值不準確這3 種準確度標準對應的時滯范圍,如附錄E 圖E1 所示。

總結上述結果,可以得出如下結論。

1）牛頓法實現準確校正的條件是迭代初值接近準確值：由譜離散化獲得的初值影響牛頓校正結果,進而影響穩定性分析準確性。

2）時滯較小時,不考慮時滯的系統特征值與時滯系統近似,即牛頓迭代初值在成功校正范圍內,經校正可以獲得準確的全部特征值。

3）隨時滯增大,計算特征值不再全部準確,只有臨界特征值準確,時滯繼續增大,迭代后全部特征值均存在誤差。

4）所提出方法會顯著增大對信息網絡的時滯分析范圍。

5）隨離散化矩陣維數增大,特征值計算準確度提高,時滯分析范圍增大,但計算時間增加,如附錄E 表E2 所 示。

根據附錄E 圖E1 所示各方法的適用范圍,針對不同的時滯研究范圍和特征值提取要求,選擇不同的離散化方案。

對于全部特征值準確計算的目標,由附錄E 圖E1 中藍色折線可以看出：①當τ≤0.5 s 時,選擇不考慮通信環節時滯系統為初始狀態的牛頓迭代法；②當時滯范圍擴大到0.5～30 s 時,采用N=10 的譜特征方法；③繼續增大研究時滯范圍,相應采用的N也變大。而當特征值提取要求降低時,如進行穩定性分析時,只需保證臨界特征值計算準確,如附錄E圖E1 中紅色折線所示。

基于此,可以針對用戶需求（時滯研究范圍和特征值提取要求（全部/臨界特征值準確））對方法進行選擇。

隨后在不同離散化維數設置下,對系統穩定域進行求解。首先改變離散化矩陣維數,在N=10,N=20,N≥30 的 設 置 下,在N=10 和N=20 離 散化方案下刻畫3.1 節算例中穩定域,如附錄E 圖E2和圖E3 所示。

在N≥30 方案下,獲得的穩定域與3.1 節一致,如圖3 中紅色區域所示。經驗證該結果與仿真（MATLAB,Simulink）一致,如附錄E 圖E4 所示。

結合附錄E 圖E2、圖E3 和圖3 分析可知,在N較小時,隨時滯增大,會出現穩定域刻畫不準確的現象。但是在N≥30 參數設置下,均可以獲得準確穩定域,且計算效率較高。

附錄E 表E2 給出了不同離散化維數設置下的穩定域求解方法的迭代次數和計算時間等信息。通過對比分析可知：隨離散化維數增大,譜離散所得特征值準確性提高,導致牛頓校正迭代次數變小。但由于矩陣維數變大,單次特征值計算時間增加,刻畫穩定域效率下降,但時滯分析范圍顯著上升。

對附錄E 圖E2、圖E3 和圖3 呈現的規律進一步細化,以N=2 為步長,研究穩定域計算準確度（判斷準確區域與總區域點數之比）與N的對應關系,結果顯示：N增大到24 后,已經可以實現準確刻畫穩定域,隨后增大N,準確度不會再提升但計算效率下降。基于此,可依據用戶需求,選擇離散化方案,以尋求計算準確度與計算速度之間的平衡。

總結上述結果,可得出如下結論。

1）本文提出方法,與以不考慮通信環節時滯的系統為初始狀態進行牛頓迭代相比,會顯著增大對信息網絡的時滯分析范圍,實現在時滯較大時,仍能準確高效捕捉系統特征值。

2）采用譜特征提取法評估系統穩定性時,隨離散化維數增大,時滯分析范圍增大,穩定域準確度提高但速度下降。在N=30 內可以獲取準確穩定域且實現較高效率。

3.2.2 與LMI 方法的比較

一般來說,利用李雅普諾夫定理引入保守性。一些研究不斷對時域法進行優化試圖減少判據保守性。參考文獻［25］基于Lyaponuv 理論和LMI 方法,利用基于Writinger 的改進積分不等式提出了時滯穩定性準則。其判據被公認為保守性很小。為此,將本文方法與其對比,并基于2 種方法分別對3.1 節算例中的系統穩定域進行刻畫。結果如圖3所示。從圖中可以看出,該算法仍存在不可避免的保守性,求得的穩定裕度小于系統實際穩定邊界值,并且不能計算出第1 個穩定域之后隨時滯增大再次出現的穩定域。而本文提出方法解決了傳統LMI方法保守性的問題,可以準確刻畫系統全部穩定域。

3.3 考慮EV 時滯與電力系統調度網絡時滯的雙時滯系統算例

為進一步驗證本文所提方法,并研究EV 時滯與系統調度網絡時滯的區別。本節構建考慮EV 時滯與系統調度網絡時滯的信息能源系統,綜合考慮發電單元與EV 引入時滯,考慮時滯后發電單元模型如圖4 所示,整個系統動態及狀態空間方程如附錄F 所示。

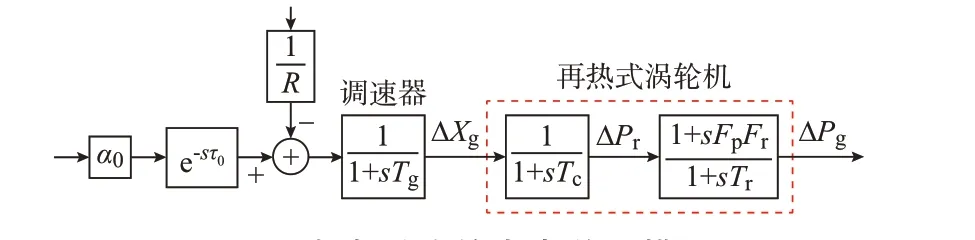
圖4 考慮時滯的發電單元模型Fig.4 Power generation unit model considering delays

采用本文提出方法,在KP=0.2 和KI=0.2 的參數設置下,首先固定發電單元時滯不變（τ0=5 s）,研究不同離散化維數下特征值準確度與EV 時滯的對應關系、結果如附錄G 表G1 所示。隨后固定EV時滯（τ1=5 s）,特征值準確度與發電單元時滯的關系如附錄G 表G2 所示。

對比2 個表格,可以觀察到固定τ0時該方法對τ1的時滯分析范圍比固定τ1時對τ0的分析范圍更大,附錄G 圖G1 解釋了該結果：固定τ0時,隨著τ1增大,臨界特征值會逐漸收斂于固定值不再變化,因而在較小的離散化維數下可以獲得更大的時滯分析范圍。而固定τ1增大τ0,臨界特征值不會收斂,因而時滯分析范圍相對較小。

隨后采用提出方法（N=30）,在τ0∈[0,100]s,τ1∈[0,100]s 的研究范圍內,求解系統穩定域,如圖5 所示。

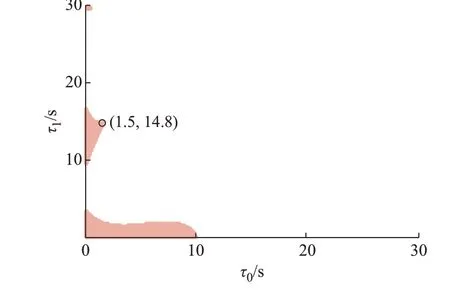
圖5 信息能源系統穩定域Fig.5 Stability region of cyber-energy system

1）EV 時滯的穩定域呈現3 個區間（τ0=0 s,τ1=30 s 處存在一個小區間）,而對于發電單元時滯,則存在一個確定的穩定裕度,當時滯小于裕度系統穩定,超過裕度系統失穩。

2）EV 時滯比發電單元時滯對系統穩定域影響大,如圖5 所示。當τ0在[0,10]s 范圍內取值時,系統存在穩定域（在τ0∈[0,10]s 范圍畫豎線,均有穩定域與直線相交）；當τ1∈[4,10]s 時,無論τ0取值為多少,系統均不穩定。

以N=2 為步長,研究穩定域計算準確度與N的關系,結果繪制于附錄G 圖G2。在N增大到14后,可以實現準確刻畫穩定域。

進一步,對EV 與發電單元對系統穩定性產生不同影響的原因進行探究,結果如附錄H 所示。

4 結語

本文提出了一種含EV 集群調頻的信息能源系統譜特征和穩定性評估方法。利用譜變換、譜離散、牛頓迭代等關鍵技術,計算得到系統特征值,對信息能源系統進行穩定性綜合評估。

1）含EV 集群調頻的信息能源系統的穩定性分析結果表明,該方法能夠較準確且高效地求解信息能源系統特征值。

2）基于譜特征提取方法分析穩定性時,準確求解特征值的時滯范圍與離散化維數有關,當N在30以內,可以獲得全部準確穩定域；再增加系統維數,計算效率下降。

3）基于用戶需求,可以對穩定性評估方法進行選擇,以尋求計算準確度與速度間的平衡。

4）綜合考慮EV 時滯與電力系統調度網絡時滯的算例結果揭示了EV 時滯與調度網絡時滯對系統穩定域影響的區別：前者的穩定域呈現若干個區間,而后者則是存在一個確定的穩定裕度。同時,EV時滯對系統穩定域的影響更大。

本文提出方法存在當時滯很大時為了保證準確性使得離散化維數增大從而導致計算效率下降的局限性。今后的工作中將進一步對系統進行降維以實現更高的計算效率。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。