灰色馬爾科夫模型在建筑事故預測中的應用

周琳琳 陳 強 周銀波

(1.河南省中衢建筑設計有限公司，河南 鄭州 450000； 2.鄭州局集團有限公司鄭州工務機械段，河南 鄭州 450052； 3.河南工程學院資源與安全工程學院，河南 鄭州 451191)

1 研究背景

近年來，我國基礎設施建設穩步發展，建筑業行業資金和人員投入也大大增加，但是我國建筑技術和管理水平仍然處在發展階段[1]。相關數據表明，自2007年至2016年10年之間，我國建筑事故發生率和死亡率分別下降27.71%，28.66%[2]。事故發生次數整體呈下降趨勢，但引發建筑事故的因素卻無法避免。為了科學提高政府等部門對建筑施工的監察力度，需要對建筑事故發生次數進行預測，保障經濟健康穩定發展。目前針對事故的預測方法較多，例如回歸分析法、神經網絡預測法、灰色預測模型、馬爾科夫預測模型等，其中灰色預測模型和馬爾科夫預測模型應用較多[3,4]。由于灰色預測模型應用簡便，但是預測結果波動性較大，存在很大局限性，為了提高預測精度可采用馬爾科夫模型對灰色預測結果進行修正。潘麗等[3]采用灰色馬爾科夫模型對上海鐵路客運量進行了預測，該方法可有效降低灰色模型的誤差。柳子暉等[4]將該方法應用到瀝青磨耗層性能預測上，對比了3種養護技術的差異。周倩倩等[5]在歷年江蘇冷鏈物流數據的基礎上，對后續幾年的需求量進行了預測，為江蘇物流行業提供了數據參考。灰色預測法和馬爾科夫模型廣泛應用于隨機事件的預測，建筑事故的發生受到外界因素影響較大，存在較大的波動性。單一灰色理論在該類型數據預測中誤差較大，很難達到預期精度，而馬爾科夫模型則能較好的描述隨機變化對象的動態趨勢，可以彌補灰色理論的不足。灰色馬爾科夫預測模型可在實際數據的基礎上，對未來狀態的發展進行科學預測可在不同的領域進行應用。本文以河北省建筑事故發生統計數據為基礎，采用灰色馬爾科夫預測模型對事故發生的次數進行預測，為建筑施工管理提供參考。

2 模型建立

2.1 灰色模型

灰色預測模型GM(1，1)模型是一種動態預測方法，可通過累加或累減對統計數據進行處理。它的構建以原始數據序列為基礎，建立過程如下：

原始序列：

X(0)=[x0(1)x0(2) …x0(n)]

(1)

累加序列：

X(1)=[x1(1)x1(2) …x1(n)]

(2)

建立具有增長趨勢序列X(1)的一階微分方程：

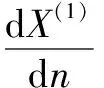
(3)

求解得到GM(1，1)模型：

(4)

(5)

式子中a,b可采用最小二乘法計算得到：

(6)

其中,

(7)

2.2 馬爾科夫模型

基于隨機過程理論，由馬爾科夫年提出并發展而成的一種常用的預測方法，它將時間設置為隨機變量，以當前狀態為基礎，通過狀態轉移矩陣來對事物發展的下一狀態進行預測。通過對灰色預測GM(1，1)模型中的數據進行狀態劃分，假設事物發展具有n個狀態，即E1，E2,…,En，建立轉移概率矩陣Pn，概述事物由狀態Ei隨機轉移到狀態Ej的轉移概率。樣本量較少時可采用一步轉換矩陣。

(8)

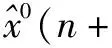
(9)

其中，N1，N2均為狀態區間的邊界值，當狀態處于高估時取正，低估時取負。

3 預測方法在建筑事故中的應用

3.1 灰色預測模型結果

河北省建筑行業2009年—2015年事故發生統計結果見表1，數據均來自于相關事故通報[6]。

表1 河北省2009年—2015年歷年建筑事故發生次數

選取2009年—2015年數據組成原始數列X(0)=[21 14 22 7 9 6 9]，根據GM(1，1)模型建立過程可得到：

X(1)=[21 35 57 64 73 79 88]

(10)

根據式(6)，式(7)和式(10)求得a=0.19，b=22.57，代入式(4)得到GM(1,1)模型：

(11)

根據灰色預測模型方程，可得到灰色預測結果如表2所示。

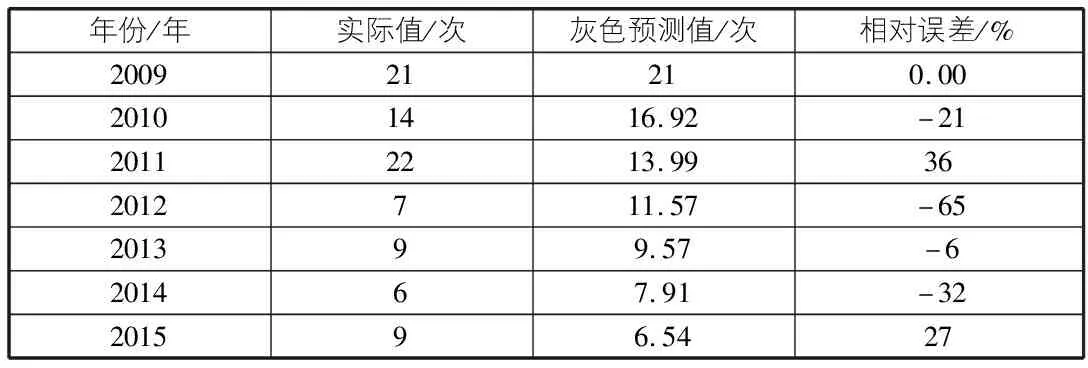
表2 河北省建筑事故發生次數灰色預測結果

3.2 馬爾科夫模型修正預測值

表2中相對誤差結果顯示，灰色預測值與實際值之間的誤差范圍為(-0.65，0.36)，由于樣本數較少，可將各年事故發生狀態劃分為三種：E1(-0.65，-0.31),E2(-0.31，0.03),E3(0.03，0.36)，得到2006年—2015年各年所處狀態，見表3。

表3 2006年—2015年各年所處狀態

根據表3結果，可得到一步狀態轉移矩陣：

(12)

根據一步轉移狀態矩陣，對灰色預測值采用馬爾科夫修正，得到結果如表4所示。

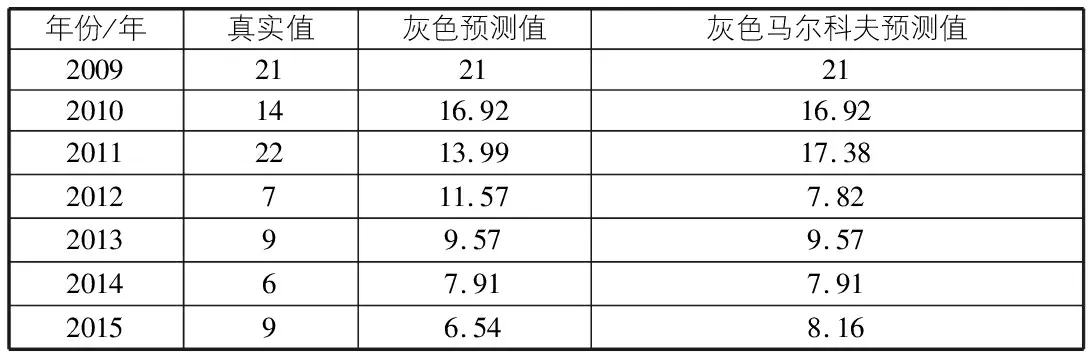
表4 模型預測結果對比

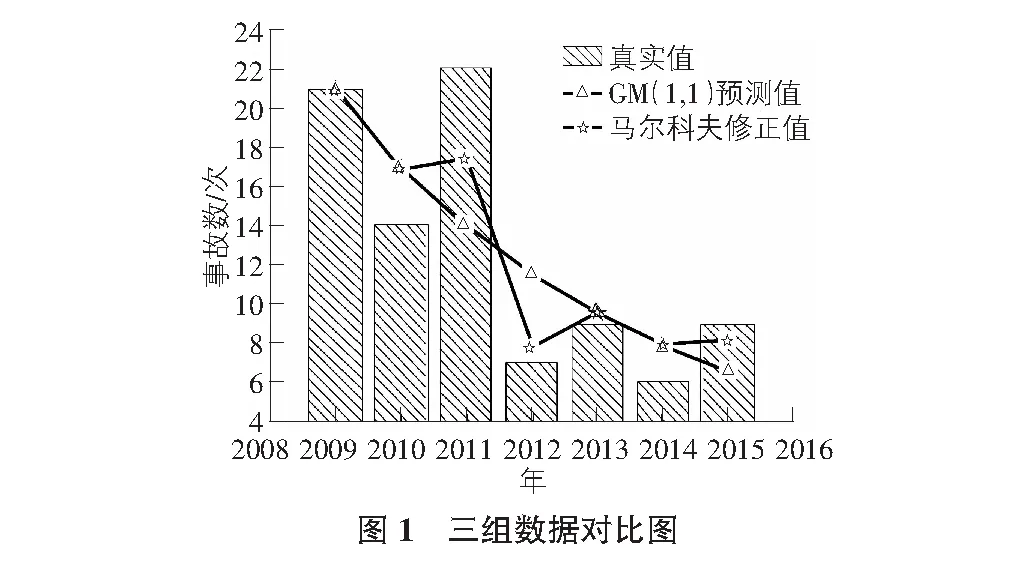
3.3 真實值、灰色預測值與馬爾科夫修正值對比結果

圖1對比了真實值、灰色預測值和灰色馬爾科夫預測值三組數據，灰色預測結果大致呈冪函數下降趨勢，與個別真實值之間誤差較大，表2結果顯示最大誤差可達0.65。由于灰色預測模型的局限性無法對數據發展的波動性進行預測，通過采用馬爾科夫模型對灰色預測模型結果進行修正可發現，在部分誤差較大的數據點，修正后的灰色馬爾科夫結果更加接近真實值。因此，采用灰色馬爾科夫預測模型可結合兩種模型優點，提高預測精度。

3.4 灰色馬爾科夫預測模型對事故次數發展的預測結果

灰色馬爾科夫模型在預測精度上優于灰色預測模型，在上述數據的計算基礎上對2016年—2022年事故發生次數進行了進一步預測。表3顯示，2015年為狀態E3，根據一步轉移矩陣公式得到2016年所處狀態為E1，灰色預測結果為5.41，灰色馬爾科夫模型預測結果為3.66。2016年事故發生次數真實值為4，可見灰色馬爾科夫具有較高的預測精度。同理可得2017年—2027年河北省建筑事故發生次數的預測結果見表5。結果顯示，建筑事故發生次數穩步下降，由于事故發生影響因素較多，真實情況將有所波動。通過對事故預測有利于相關部門進行參考，以便采取更加有利的措施預防事故。

表5 灰色馬爾科夫對2017年—2022年建筑事故發生次數的預測結果

4 結語

1)建筑事故次數可采用灰色預測法進行初步預測，但是其誤差較大，最大可達0.65，不能準確反映事故發生的發展趨勢，需要提高其預測精度。

2)灰色馬爾科夫模型具有更高的預測精度，預測結果能夠有效的反映實際狀況，河北省建筑事故次數預測結果顯示，隨著時間延長事故次數逐漸下降，該模型可有效反映該省的事故次數的發展趨勢，可對建筑業事故發生、死亡人數等相關數據預測，為監管部門提供數據基礎。