處理立體幾何客觀題的４種思維方式

◇ 山東 劉 英

立體幾何是考查學生空間想象能力及推理論證能力的主要題型,通常與立體幾何有關的客觀題,都是小題,但解題方法靈活,解題中除了要熟練掌握空間點、線、面之間的關系及平面幾何圖形的有關性質外,還要掌握一些特殊的解題思維,如折疊、展開、分割、補形等．

1 折疊

例1(2020年全國卷Ⅰ)如圖1所示,在三棱錐P-ABC的平面展開圖中,AC＝AB⊥AD,∠CAE＝ 30°,則cos∠FCB＝__________．

解析知條件得PA,AB⊥AC,∠CAP＝30°,故求cos∠FCB,即求cos∠PCB．

將平面圖形折疊成三棱錐(如圖2所示),由已

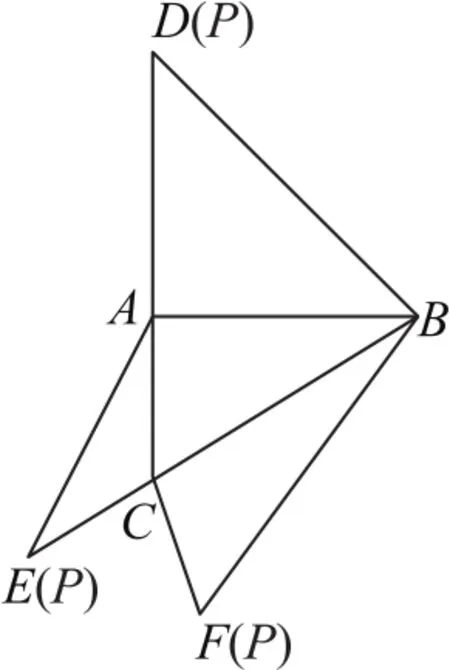
圖1

在△PAC中,AC＝1,,由余弦定理得PC2＝3＋1－,所以PC＝1．

圖2

在Rt△ABC中,AB＝,則BC＝2．同理在Rt△PAB中,有PB＝．所以在△PBC中,由余弦定理得cos∠PCB＝

解析

本題給出了三棱錐的平面展開圖,可按要求將其折疊成空間幾何體,再結合已知條件求解．應用此類思維方式解題時要注意平面展開圖與立體圖形中點、線、面的對應關系．

2 展開

例2如圖3所示,P是圓錐的頂點,O是底面的圓心,AB為直徑,點C是圓O上異于A,B的點,且PO＝OB＝1,,點E在線段PB上,則CE＋OE的最小值為________．

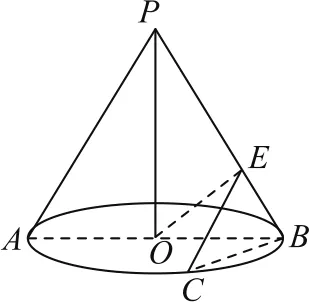
圖3

解析

在△POB中,PO＝所以．連接PC,同理可得．所以在△PBC中,PB＝

在三棱錐P-ABC中,將側面PCB繞PB旋轉至平面PBC′的位置,使其與平面PAB共面,如圖4所示．當點O,E,C′共線時,CE＋OE的值最小．

圖4

在△OC′P中,由余弦定理得

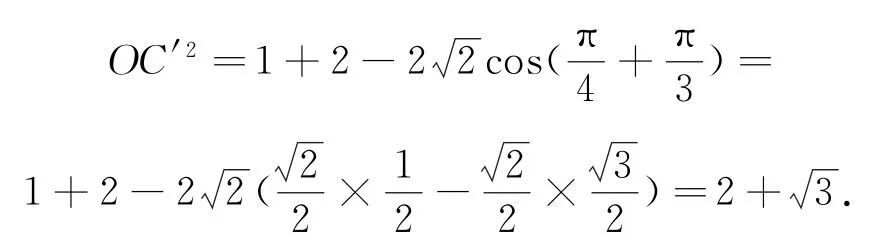
點評

空間問題平面化是解答立體幾何問題的重要思維方式,特別是在處理空間幾何體表面上動點到兩定點間距離之和最小時,將空間中的面展開,則可將問題轉化為平面內動點到兩定點距離之和最小問題．

3 分割

例3如圖5所示,在棱長為1的正方體ABCD-A1B1C1D1中,E是棱CC1上的一個動點,平面BED1交棱AA1于點F,則四棱錐B1-BED1F的體積為( )．

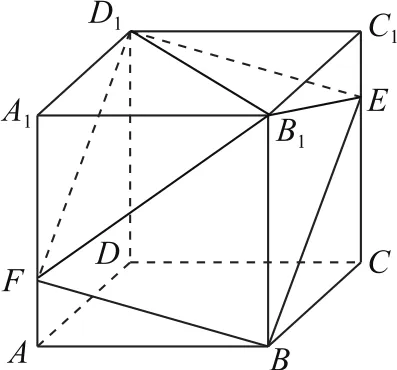
圖5

解析

如圖6所示,連接BD1,則可將四棱錐B1-BED1F分割成兩個三棱錐D1-BFB1,D1-BB1E．設h1為D1到平面BFB1的距離,h2為D1到平面BB1E的距離,則

所以四棱錐B1-BED1F的體積為．故選B．

點評

本題若直接求四棱錐B1-BED1F的體積,其底面積和高都不易求得,通過分割法將不規則幾何體轉化為規則幾何體,計算方便,從而快速求得結論．

圖6

4 補形

例4如圖7所示,在三棱錐P-ABC中,PA⊥,PA和BC的公垂線ED交PA于點E,交BC于點D,ED＝3,則三棱錐P-ABC的體積為( )．

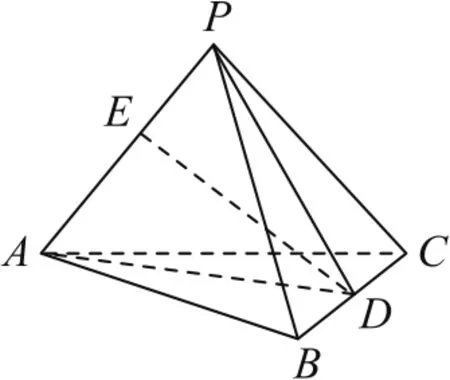
圖7

解析

如圖8所示,以△ABC為底面,PA為側棱,將三棱錐P-ABC補為三棱柱PB1C1-ABC,連接EB,EC．因為PA⊥BC,PA⊥DE,所以PA⊥平面BEC,所以

圖8

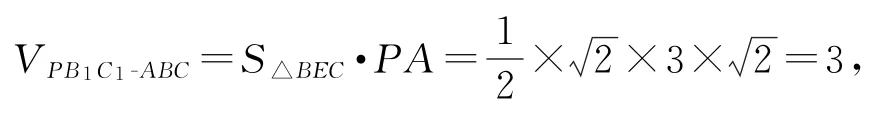
點評

通過補形法,將不規則的幾何體構造為特殊的幾何體(特殊的幾何體一般指長方體、正方體、三棱柱等),從而將其中隱含的幾何關系直觀地體現出來,即化隱為顯,進而準確找到解題的切入點．

綜上所述,折疊、展開、分割、補形是處理空間幾何問題的重要思維方式,教學中教師要培養學生觀察、想象、轉化能力,靈活應用各種思維,進而提高學生綜合問題的求解能力．