巧借周期性,妙解數列題
◇ 山東 劉 麗
數列是一種特殊的函數,所以一些數列問題中也存在著包括周期性在內的和函數基本性質相關的問題.有些數列問題,表面上看似與周期性無關,實際上隱含著周期性,若不加以分析,很難找到求解策略,而一旦找到數列中的周期性,問題往往便迎刃而解了.本文結合實例論述巧借周期性,妙解數列題.
1 求解和式遞推數列中的項
例1在數列{an}中,a1=1,a2=3,對所有自然數n都有an+2=|an+1|-an,則a2019的值為_______.
解析
由題意和遞推關系式an+2=|an+1|-an,結合a1=1,a2=3,易求得a3=2,a4=-1,a5=-1,a6=2,a7=3,a8=1,a9=-2,a10=1,a11=3,a12=2,…,于是歸納可知數列{an}具有周期性,其周期為9,所以a2019=a224×9+3=a3=2.
點評
利用條件中的和式遞推關系式加以歸納處理,這是破解此類和式遞推數列周期性問題的技巧.根據數列的和式遞推關系式進行逐個推導,求解難度比較大,計算比較煩瑣,有時還無從下手.而通過遞推關系式分析后結合相應的規律歸納其周期性,一般中見特殊,可使問題快速獲解.
2 求解分式遞推數列中的項
例2已知數列{an}滿足a1=1,a2=2,且對任何自然數n都有,則a2019的值為_________.
解析
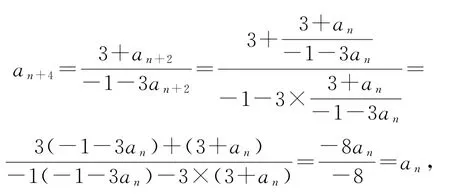
故數列{an}是以4為周期的數列,結合a1=1,a2=2,可得,所以
點評
利用條件中的分式遞推關系式加以迭代處理,這是破解此類分式遞推數列周期性的技巧.在采用迭代法時要注意的是如何確定迭代的分式解析式.
3 求解遞推數列的前n項和
例3已知數列{an}滿足a1=a2=1,a3=2,且對任何自然數n都有anan+1an+2≠1,又anan+1an+2·an+3=an+an+1+an+2+an+3,記Sn為數列{an}的前n項和,則S2019=________.
解析
由于anan+1an+2an+3=an+an+1+an+2+an+3,則有a1a2a3a4=a1+a2+a3+a4,結合a1=a2=1,a3=2,解得a4=4,則a1+a2+a3+a4=1+1+2+4=8.
又由anan+1an+2an+3=an+an+1+an+2+an+3,得an+1an+2an+3an+4=an+1+an+2+an+3+an+4,以上兩式對應相減,可得an+1an+2an+3(an-an+4)=an-an+4,整理得(an+1an+2an+3-1)(an-an+4)=0,而對任何自然數n都有anan+1an+2≠1,所以anan+4=0,即an+4=an,故數列{an}是以4為周期的數列,那么S2019=(a1+a2+a3+a4)×505-a2020=8×505-4=4036.
點評
利用遞推公式一項一項地往后推導,再加以求和,解答過程比較繁雜且計算量明顯較大.通過分析數列的遞推公式,確定周期規律,充分利用函數與方程的性質與思想,結合周期性來解決較為簡捷.
4 求解創新定義下數列的前n項和
例4在數列{an}中,如果對于任意n∈N*,都有anan+1an+2=k(k為不為零的常數),那么這個數列稱為“等積數列”,其中常數k稱為這個數列的公積.已知數列{an}是一個“等積數列”,且滿足a1=1,a2=2,公積為8,則數列{an}前2021項和S2021的值為________.
解析根據創新定義可知anan+1an+2=k,則有an+1an+2an+3=k,兩式對應作商,得1,即an+3=an,故數列{an}是以3為周期的數列,結合a1=1,a2=2,k=8,可得a3=4,所以S2021=a1+a2+a3+…+a2021=(a1+a2+a3)×673+a1+a2=7×673+1+2=4714.
點評
本題求解的關鍵是抓住“等積數列”的創新定義,對兩個數列關系式作商并整理得到an+3=an,進而確定數列的周期.求解此類創新定義問題,要正確理解并掌握條件中所敘述的創新定義的實質,將其轉化為相關的數列關系式,進而加以轉化與應用.
5 求解數列的前n項積
例5已知數列{an}滿足a1=3,且滿足an+1=,則數列{an}前2021項的積a1·a2·a3·…·a2021的值為________.
解析
令an=tanxn,則有
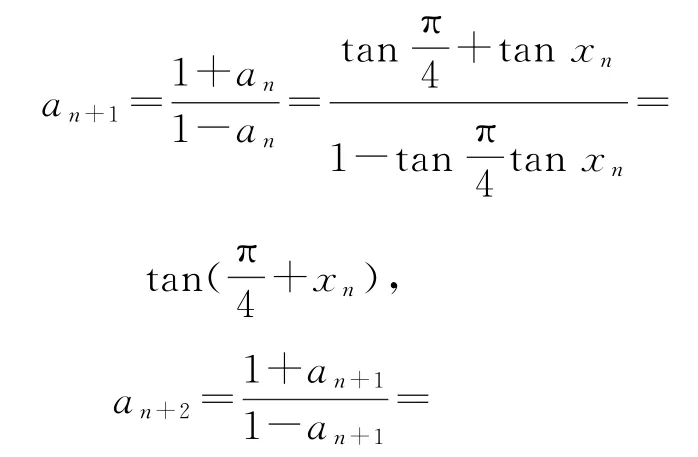
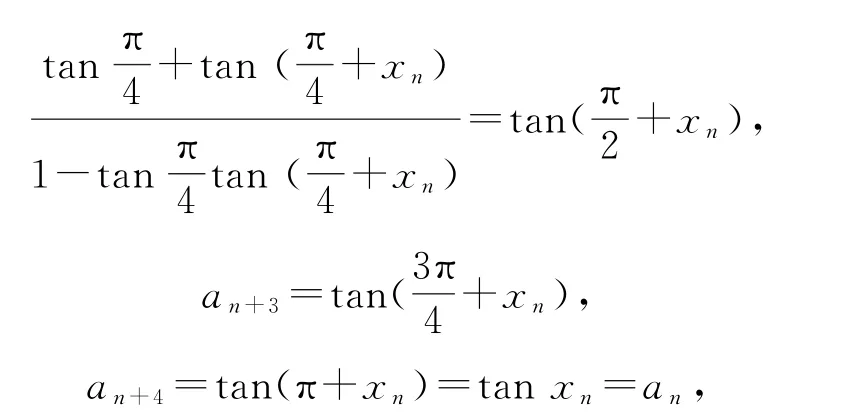
故數列{an}是以4為周期的數列,而結合遞推關系可得,則a·a·a·123a4=1,所以數列{an}前2021項的積a1·a2·a3·…·a2021=a2021=a1=3.
點評
根據數列的遞推關系式,聯想到三角函數的正切公式,結合三角函數的相關知識來確定數列的周期問題,在此基礎上確定數列的前n項積.
在破解涉及周期性的數列問題時,利用歸納法、迭代法、加減相消法、三角函數法、創新定義法等來巧妙轉化,進而確定數列的周期性,為破解數列中的項、前n項和或積等問題提供條件.破解此類問題的關鍵是從題目條件中挖掘相應的條件,找到撬動數列周期的支點,從而采用切實可行的方法加以剖析.

