區(qū)分快慢變子系統(tǒng)的柔性機械臂控制方法

孫紹林

（貴州大學(xué)繼續(xù)教育學(xué)院，貴州 貴陽 550025）

1 引言

相比于傳統(tǒng)剛性機械臂，柔性機械臂因材質(zhì)輕、高精度、高速度、低能耗等優(yōu)勢而應(yīng)用廣泛，但是柔性機械臂的長時間振動會影響系統(tǒng)定位精度，同時降低系統(tǒng)使用壽命，因此抑制甚至消除柔性機械臂振動意義重大。

柔性機械臂常用的控制方法包括PID 控制、模糊控制、最優(yōu)控制、反演控制、變結(jié)構(gòu)控制、魯棒控制、能量法等。文獻[1]使用改進PID 控制器抑制柔性機械臂末端振動，取得了一定效果；文獻[2]使用遺傳算法優(yōu)化模糊控制，抑振效果明顯優(yōu)于傳統(tǒng)模糊控制；文獻[3]使用反演控制法控制焊接機器人，取得了滿意效果；文獻[4]用變結(jié)構(gòu)控制與Haar 小波結(jié)合對工業(yè)機械臂位置進行控制，控制精度較高；文獻[5]提出了改進和聲搜索-遺傳算法的魯棒控制器，與其他魯棒控制器相比，在超調(diào)量、調(diào)節(jié)時間上具有優(yōu)勢；文獻[6]分別使用PID 法和能量法對末端振動進行控制，實驗驗證了能量法的準確性、可行性。當(dāng)前對柔性機械臂跟蹤精度、振動抑制要求越來越高，單一控制方法已難以滿足要求。

使用奇異攝動法將柔性機械臂系統(tǒng)分解為快慢變兩個子系統(tǒng)，使用反演滑模變結(jié)構(gòu)設(shè)計慢變子系統(tǒng)控制器，使用模糊控制設(shè)計快變子系統(tǒng)控制器，而后將快慢變控制律組合得到最終控制律。

經(jīng)仿真驗證，與傳統(tǒng)PID 控制相比，組合控制在轉(zhuǎn)角誤差、穩(wěn)定時間、末端振動量、轉(zhuǎn)角速度等多個方面優(yōu)勢明顯。

2 柔性機械臂動力學(xué)建模

由于柔性機械臂粗長比極小，故機械臂梁模型選用Euler-Be-rnoulli 梁。柔性機械臂彈性變形描述準確性影響動力學(xué)模型準確性，鑒于假設(shè)模態(tài)法計算量小、效率高等優(yōu)點，使用假設(shè)模態(tài)法描述柔性機械臂的彈性形變。

2.1 柔性機械臂彈性變形

單桿柔性機械臂示意圖，如圖1 所示。圖中OX0Y0 為慣性坐標系，OX1Y1 為切線坐標系，機械臂一端連接驅(qū)動電機，另一端連接質(zhì)量塊m，u 為控制力矩，Jh為電機轉(zhuǎn)動慣量，E 為彈性模量，I 為橫截面對中性軸慣量矩，L 為機械臂長度，A 為橫截面積，ρ 為材料密度，θ（t）為剛性轉(zhuǎn)角，w（x，t）為點 P（橫坐標為 x）在 t 時刻的橫向彈性變形。

圖1 單桿柔性機械臂模型Fig.1 Single Arm Flexible Manipulator Model

由假設(shè)模態(tài)法可知，機械臂橫向彈性變形量w（x，t）為：

式中：n—模態(tài)數(shù)；Wi（x）—柔性機械臂固有振型函數(shù)；qi（t）—模態(tài)坐標。參考文獻[7-8]，系統(tǒng)彈性形變主要集中在前2 階模態(tài)，故n=2。

2.2 柔性機械臂能量分析

柔性機械臂動能T 由兩部分組成，分別為機械臂動能T1和質(zhì)量塊動能T2。機械臂自身動能T1為：

質(zhì)量塊動能T2為：

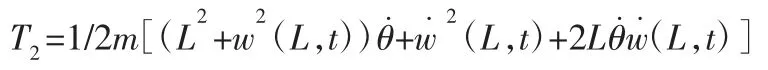
則柔性機械臂總動能T=T1+T2。

柔性機械臂運動方式為在水平面內(nèi)做旋轉(zhuǎn)運動，因此計算勢能時不考慮重力勢能，只考慮彈性勢能，為：

2.3 柔性機械臂動力學(xué)模型

使用拉格朗日方程建立柔性機械臂動力學(xué)方程，拉格朗日方程描述為：

式中：L=T-U—拉格朗日函數(shù)；Q—廣義力；z—廣義坐標變量。將機械臂系統(tǒng)動能和勢能代入式（2），解得動力學(xué)方程為：

式中：M—慣性矩陣；G—哥氏力和離心力矩的交叉耦合矩陣；K—剛度矩陣；u—機械臂控制力矩，p=［θ，q1，…，qn］T，F(xiàn)=［1，0，…，0］T。

3 系統(tǒng)組合控制原理

3.1 快慢變子系統(tǒng)分解方法

上節(jié)中提到，模態(tài)數(shù)n=2 較為合適，那么單桿柔性機械臂系統(tǒng)動力學(xué)方程可表達為：

由于慣性矩陣M 為正定矩陣，則其逆矩陣必然存在，記為H，則：

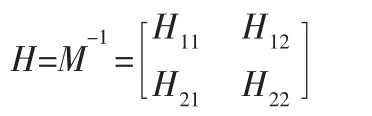
對式（4）左乘矩陣H，可得：

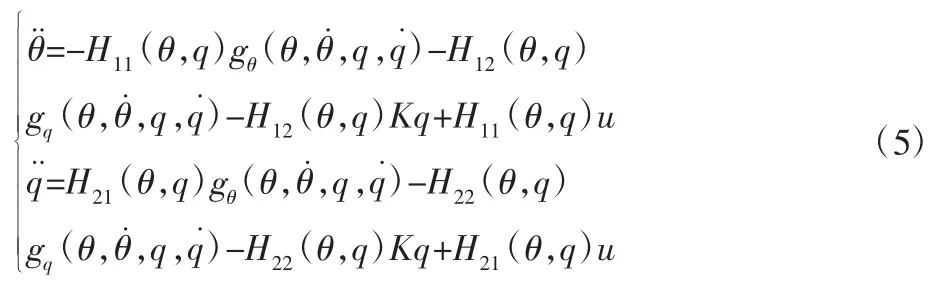
小參數(shù)μ 的存在使奇異攝動方程在快變量中顯示邊界層現(xiàn)象。將系統(tǒng)模型進行奇異分解[9]，可以將快變子系統(tǒng)與慢變子系統(tǒng)分開。

令μ=0，由奇異攝動模型可以推導(dǎo)出慢變子系統(tǒng)動力學(xué)方程為：

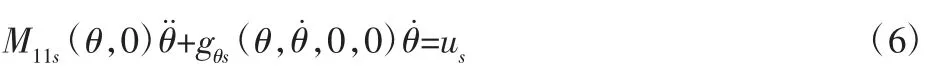
其中下標s 表示此量為慢變量。

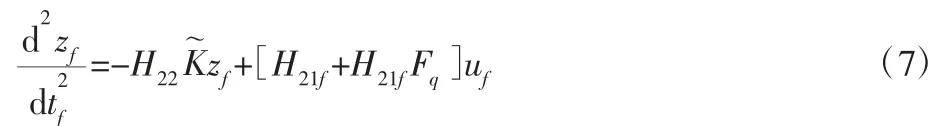
其中下標f 表示此量為快變量，用于描述柔性機械臂的彈性振動過程。

3.2 快慢變子系統(tǒng)組合控制原理

慢變子系統(tǒng)描述機械臂的剛性轉(zhuǎn)動過程，快變子系統(tǒng)描述柔性機械臂的彈性振動過程。慢變子系統(tǒng)具有較強的非線性和參數(shù)不確定性，滑模變結(jié)構(gòu)控制對參數(shù)變化或θ 擾動不敏感，具有很強的魯棒性，但是存在抖振問題；反演控制能夠很好解決滑模變結(jié)構(gòu)抖振問題，因此將反演控制與滑模變結(jié)構(gòu)控制相結(jié)合，提出了慢變子系統(tǒng)的反演滑模變結(jié)構(gòu)控制。

快變子系統(tǒng)是非線性時變系統(tǒng)，難以實現(xiàn)較為精確的控制。模糊控制不需要精確數(shù)學(xué)模型，具有較強容錯能力，特別適用于非線性、強耦合、時變、滯后系統(tǒng)，因此選擇模糊控制用于快變子系統(tǒng)控制。則柔性機械臂組合控制原理，如圖2 所示。

圖2 柔性機械臂組合控制原理Fig.2 Composite Control Principle of Flexible Manipulator

4 快慢變子系統(tǒng)組合控制器設(shè)計

4.1 慢變子系統(tǒng)控制器

使用反演滑模變結(jié)構(gòu)控制法設(shè)計慢變子系統(tǒng)控制器。為簡化表達，將快變量下標 f 和慢變量下標 s 省略。記 x1=θ，x2=θ˙，那么式（6）可改寫為：

記機械臂期望剛性轉(zhuǎn)角為xd，要求xd具有二階導(dǎo)數(shù)，則誤差為定義虛擬控制量為，式中 c1>0

定義第一個Lyapunov 函數(shù)為V1=1/2e21，則：

定義切換函數(shù)σ=k1e1+e2，式中k1>0，將虛擬控制量代入切換函數(shù)，得：

易知式中 k1+c1>0，當(dāng)滑模面 σ=0，則異號，則≤0，因此進行下一步設(shè)計。

定義第二個Lyapunov 函數(shù)為V2=V1+1/2σ2，則：

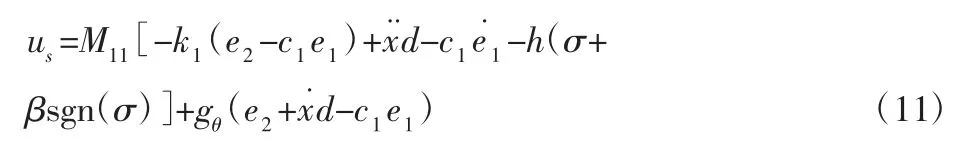
式中：h、β—常數(shù)，且 h>0、β>0；sgn（）—符號函數(shù)。

4.2 快變子系統(tǒng)控制器

考慮到快變子系統(tǒng)模型不準確，而模糊控制能夠彌補模型不準確的影響[10-11]，所以設(shè)計了抑制振動的模糊控制器。

記機械臂末端振動誤差值為e、誤差變化率為ec，則模糊控制器輸入量為e、ec，輸出量為uf。

（1）精確量的模糊化。對于模糊控制，等級劃分越細致則控制精度越高，但是計算量也會大大增加。模糊論域采用八段式，即將輸入量和輸出量變換到｛NB，NM，NS，NZ，PZ，PS，PM，PB｝，分別代表負大、負中、負小、負零、正零、正小、正中、正大。確定振動誤差范圍 e∈［-0.15，0.15］，單位為 rad，振動誤差變化率范圍 ec∈［-0.05，0.08］，單位為 rad/s；控制力矩 uf∈［-10，10］，單位為 Nm。將三個變量映射到模糊域［-6，6］中，易知量化因子為kc=40，kec=92.3，比例因子ku=1.67。輸入量和輸出量的三角形隸屬度函數(shù)圖，如圖3 所示。

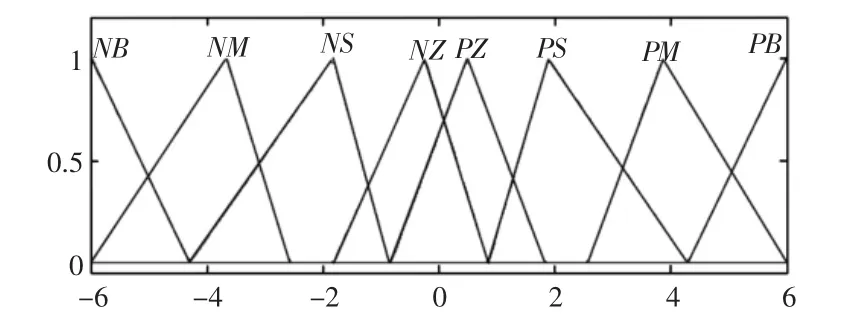
圖3 三角形隸屬度函數(shù)圖Fig.3 Triangle Membership Function

（2）制定模糊規(guī)則。模糊控制器的輸入量有兩個，輸出量有一個，每個量分為8 個等級，則需要制定64 條模糊規(guī)則。控制量的確定以減小振動為目標，即當(dāng)振動誤差較大時，以快速消除誤差為主；當(dāng)振動誤差較小時，以控制系統(tǒng)超調(diào)量為主。根據(jù)這一原則，制定模糊規(guī)則，如表1 所示。

表1 模糊控制規(guī)則Tab.1 Fuzzy Control Rule

（3）去模糊化。目前常用的去模糊化方法有重心法、最大值法、加權(quán)平均法。重心法精度最高，但是計算最復(fù)雜；最大值法相對簡單，但是誤差較大；加權(quán)平均法兼顧兩種方法優(yōu)點，因此選用加權(quán)平均法進行去模糊化，方法為：

式中：z0—去模糊化后的值；zi—模糊值；μ（cz）i—zi的隸屬度。則快變量的控制量為=ku·z0。

5 仿真驗證及分析

ADAMS 用于機械系統(tǒng)運動學(xué)和動力學(xué)仿真，但是難以設(shè)計復(fù)雜控制器，而MATLAB 擁有足夠的控制工具箱，故設(shè)計了ADAMS 與MATLAB 聯(lián)合仿真的方法，聯(lián)合仿真原理，如圖4 所示。兩軟件之間每0.05s 進行一次數(shù)據(jù)交換。

圖4 聯(lián)合仿真原理Fig.4 Unite Simulation Principle

機械臂參數(shù)為：機械臂長度L=1200mm，截面寬度為4mm，面高度為60mm，彈性模量 E=2×1011N/m，材料密度 ρ=7.8×106kg/m3，末端質(zhì)量塊m=1kg。

使用階躍響應(yīng)驗證組合控制對柔性機械臂的控制效果。柔性機械臂在水平面內(nèi)轉(zhuǎn)動，起始角度設(shè)為0，目標角度值設(shè)置為30°，仿真時間為 20s。

分別使用傳統(tǒng)PID 控制器與組合控制器控制柔性機械臂，PID 控制技術(shù)已經(jīng)成熟，在此不再贅述，使用極點配置法求解PID參數(shù)，分別為 KP＝100，Ti＝2，Td＝10。組合控制中慢變子系統(tǒng)控制器參數(shù)為h=0.5，k1=0.3，c1=1.2。PID 控制器與組合控制器作用下的轉(zhuǎn)動角，如圖5 所示。

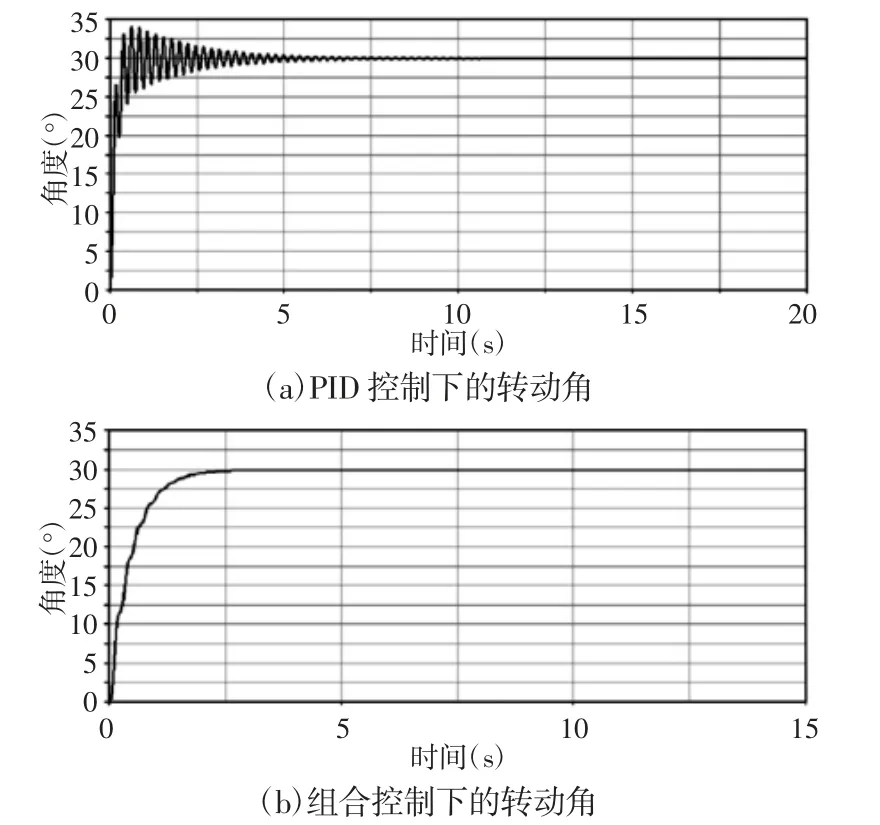
圖5 兩種控制器控制下的轉(zhuǎn)動角Fig.5 Rotating Angle under the Two Controllers

兩控制器控制下的轉(zhuǎn)動角速度，如圖6 所示。

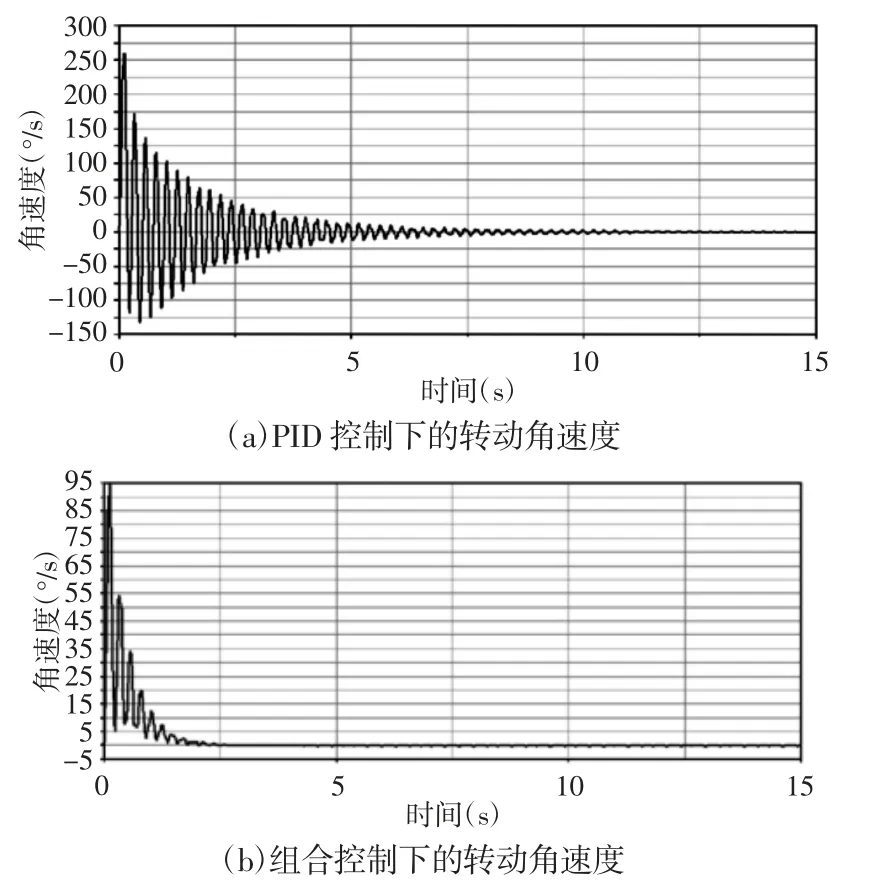
圖6 兩種控制器控制下的轉(zhuǎn)動角速度Fig.6 Rotating Angle Speed under the Two Controllers

兩控制器控制下的末端振動，如圖7 所示。

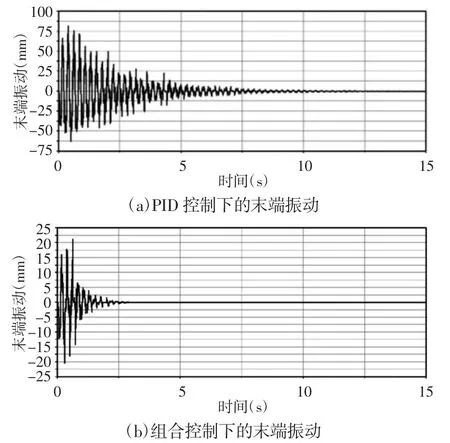
圖7 兩種控制器控制下的末端振動Fig.7 End Position Vibration Under the Two Controllers

兩控制器控制下的控制力矩，如圖8 所示。

圖8 兩種控制器控制下的控制力矩Fig.8 Control Moment Under the Two Controllers

為了更加精確地比較PID 控制器與組合控制器對柔性機械臂的控制效果，統(tǒng)計兩控制器的性能參數(shù)，如表2 所示。

表2 兩控制器控制效果對比Tab.2 Control Effect of the Two Controllers

從圖5～圖8 和表2 可以看出，與傳統(tǒng)PID 控制器相比，在組合控制下，柔性機械臂振動明顯減小，穩(wěn)定時間明顯變短，加速度最大值遠遠減小，末端振動幅值遠遠減小，力矩值遠遠減小，在節(jié)省能量同時，維護了系統(tǒng)穩(wěn)定，可以極大地保護系統(tǒng)。

組合控制器在柔性機械臂控制中性能遠遠優(yōu)于PID 控制，這是因為組合控制器針對快慢變子系統(tǒng)各自的特性，有針對性地分別設(shè)計了控制器，在減小柔性機械臂振動的同時，提高了控制精度。

6 結(jié)論

經(jīng)過分析和仿真驗證，可以得出以下結(jié)論：（1）奇異攝動法可以有效地將機械臂系統(tǒng)分解為快變子系統(tǒng)和慢變子系統(tǒng)，其中慢變子系統(tǒng)描述旋轉(zhuǎn)過程，快變子系統(tǒng)描述振動過程；（2）反演滑模變結(jié)構(gòu)可以精確控制機械臂慢變子系統(tǒng)的旋轉(zhuǎn)過程，模糊控制器可以有效抑制機械臂快變子系統(tǒng)的振動過程；（3）與傳統(tǒng)PID控制器相比，在組合控制器的控制下，柔性機械臂轉(zhuǎn)動角誤差下降了99%，穩(wěn)定時間減少了75%，最大末端振動量減少了74.1%，充分證明了組合控制器在柔性機械臂控制中的有效性。