邊坡工程中巖土錨桿設計若干問題探討

劉興遠，劉洋

（重慶市建筑科學研究院有限公司，重慶 400016）

0 引言

山區城市工程建設受地形、道路及用地紅線的限制，產生大量高、大、險的邊坡治理工程，特別是由外傾軟弱結構面控制邊坡穩定性的邊坡治理工程（含滑坡治理）大量增加，巖土錨桿[1-6]特別是預應力錨桿在邊坡工程中得到了廣泛應用。現行國家標準《建筑邊坡工程技術規范》（GB 50330—2013）中建筑邊坡主要有三種支護結構（或其組合支護結構），分別為重力式擋墻（重力式擋墻、衡重式擋墻、懸臂式混凝土擋墻、扶壁式混凝土擋墻等）、錨桿[4]（錨桿為錨桿和預應力錨索的總稱）擋墻及樁板擋墻。巖土錨桿作為重要的支護結構構件可與混凝土擋墻或抗滑樁組合，形成錨桿擋墻和錨拉樁支護結構，且該標準單列一章專門論述錨桿設計。針對巖土錨固中的錨桿，國家頒布了現行國家標準《巖土錨桿與噴射混凝土支護工程技術規范》（GB 50086—2015），該標準對預應力錨桿和非預應力錨桿的設計及應用給出了相應規定。然而，巖土錨桿在實際工程應用中仍存在若干問題值得商榷，特別是各類預應力錨桿在使用中存在諸多技術和應用問題。為此，本文以錨桿變形協調為基礎，探討錨桿和荷載分散型錨桿在設計及應用中應注意的問題，其計算和分析結果可供相關工程技術人員學習、參考。

1 巖土錨桿設計基本理論

巖土錨桿是指安裝在巖土層中，將拉力傳至穩定巖土層中的受拉構件及其體系（圖1）。巖土錨桿一般由三部分組成：錨固段、自由段和鎖定段（錨具或錨固端）。錨固段在土層中的錨桿稱為土層錨桿，錨固段在巖層中的錨桿稱為巖石錨桿。根據對錨桿桿筋是否施加預應力，錨桿又分為預應力錨桿和非預應力錨桿，《巖土錨桿與噴射混凝土支護工程技術規范》[2]（GB 50086—2015）標準將低預應力錨桿（受拉承載力低于200kN的預應力錨桿）也劃歸為非預應力錨桿。

圖1 錨桿基本構成簡圖

巖土錨桿錨固段由三部分組成：錨固段中穩定的巖土體、與巖土體和桿筋相連的錨固體（一般為水泥砂漿）、錨桿桿筋。巖土錨桿錨固段長度宜根據巖土體特性控制在8～12m以內，巖石錨固段長度控制在8m以內，土層錨固段長度控制在12m以內。桿筋一般采用鋼筋和鋼絞線，也可采用其他金屬材料或碳纖維桿材。當前錨桿桿筋通常采用鋼筋和鋼絞線。根據錨桿受力形式的差別，錨桿可分為拉力型錨桿和壓力型錨桿；根據錨桿錨固段錨桿受力特點，又可分為普通型錨桿和荷載分散型錨桿；根據錨桿桿筋是否可以重復使用，又可分為可回收錨桿和不可回收錨桿。

巖土錨桿承載力設計主要包括三個方面的計算：①錨桿桿筋用量計算，即桿筋配筋量計算；②錨桿錨固體與巖土層間的錨固長度計算；③錨桿桿筋與錨固體間的錨固長度計算。最終取3個計算值中的最小值作為巖土錨桿承載力的設計值。

巖土錨桿設計值計算選擇不同的國家現行技術標準，其計算公式基本相同，但不同國家現行技術標準的安全系數、巖土參數等參數取值有所差異，致使計算結果存在較大差別。如《建筑邊坡工程技術規范》（GB 50330—2013）與《巖土錨桿與噴射混凝土支護工程技術規范》（GB 50086—2015）計算錨桿鋼筋用量，其結果就有所差別。

算例1：某邊坡工程為永久性邊坡，邊坡安全等級為一級，錨桿軸向拉力標準值為40kN，錨桿錨孔直徑為80mm，鋼筋為HRB400，fy=360N/mm2，砂漿強度等級為 M30，錨固段巖體為極軟巖，錨桿傾角20度，試設計錨桿鋼筋配置。

現分別按 《建筑邊坡工程技術規范》（GB 50330—2013）和《巖土錨桿與噴射混凝土支護工程技術規范》（GB 50086—2015）的規定進行計算，2個標準的計算結果對比見表1。由表1計算結果獲知：按GB 50330—2013的設計規定，錨桿配置為：錨桿錨孔直徑80mm，配1根直徑為20mm的HRB400螺紋鋼筋，巖體錨固段長度3m（構造要求），砂漿強度等級M30。按GB 50086—2015的設計規定，錨桿配置為：錨桿錨孔直徑80mm，配1根直徑為16mm的HRB400螺紋鋼筋，錨固段長度3m（構造要求），砂漿強度等級M30。

表1 錨桿設計結果對比

先按上述實際桿筋配置，再按GB50330—2013的規定核算上述兩種錨桿理論承載力設計值，計算參數取值不變，計算結果對比見表2。

表2 兩種錨桿理論承載力計算結果對比（kN）

從該算例可見，按《巖土錨桿與噴射混凝土支護工程技術規范》（GB 50086—2015）設計的錨桿鋼筋用量比按《建筑邊坡工程技術規范》（GB 50330—2013）設計的錨桿鋼筋用量要少。

2 錨桿受力過程分析

現有錨桿是以強度理論作為出發點進行設計的，且假設錨桿是等強度同時發揮作用的，即現有設計暫未考慮錨桿變形協調引起的問題，也就是說未考慮錨桿變形協調問題。為了考察邊坡工程變形引起的錨桿承載力變化的實際情況，圖2給出了某巖質邊坡采用錨桿支護，邊坡工程變形引起的錨桿應力計算問題。為計算方便，圖2中A點設為第一排錨頭位置，且為邊坡變形監測點位置，D點為坡底，B點為錨桿錨固端起點。

已知參數為：邊坡理論破裂角θ，錨桿與水平線夾角α，A點處坡高Hi，則圖2中A、B、C、D點的坐標如下：

C 點坐標：（0，Hi）；

D點坐標：（Hi/tan（θ），0）；

A 點坐標：（Hi/tan（θ），Hi）；

B 點坐標 ：（tan（α）Hi/[tan2（θ） +tan （θ）tan（α）]，Hi{1-tan（α）/[tan（θ）+tan（α）]}）。

圖2 邊坡工程變形引起的錨桿應力計算示意圖

假設A點發生水平位移和豎向沉降，分別計為：δx，δy， 且假設巖體錨固段起始點 （圖2中B點）為不動點，錨桿變形后，A 點變為 A’點，A’點坐標為（x1+δx，y1+δy）。

AB 段的長度為：LAB=（（X1-X2）2+（y1-y2）2）1/2，

A’B 段的長度為：LA’B=（（X1+δx-X2）2+（y1+δy-y2）2）1/2，

錨桿應變、應力增量分別為：Δε=（LA’B-LAB）/LAB，Δσ=EΔε。

算例2（錨桿變形后鋼筋應力計算）邊坡工程相關參數如下：邊坡理論破裂角θ=43°，錨桿與水平線夾角α=20°，A點處坡高Hi=16m， 錨桿為 RHB400 鋼筋，fy=360N/mm2，E=2.0×105N/mm2，鋼絞線，fptk=1860N/mm2，fpy=1320N/mm2，鋼絞線預應力初始值為 σ控=520N/mm2，E=1.95×105N/mm2。 分析計算圖 2 所示錨桿變形后，錨桿應力增量及錨桿達到設計強度時錨桿變形量（注：計算中假設錨桿抗力由錨桿配筋強度控制，后面所有算例均有此假設）。

C 點 坐 標 ： （0，16）；D 點 坐 標 ： （17.158，0）；A 點 坐 標 ：（17.158，16）；B 點坐標：（4.817，11.508）。

假設A點水平位移和豎向沉降分別為：δx=10mm，δy=10mm，則錨桿變形后，A 點變為 A’點，A’點坐標為（17.168 ，15.990）。

AB 段 的 長 度 為 ：LAB=13.133m；A’B 段 的 長 度 為 ：LA’B=13.139m。

下面分別按鋼筋和鋼絞線兩種情況，考察A點變形引起的應變、應力增量問題。

（1）AB為鋼筋錨桿的計算

在上述變形條件下，錨桿鋼筋應變、應力增量分別為：Δε=4.56×10-4，Δσ=91.1N/mm2。

假設錨桿變形，鋼筋達到其強度設計值，此時鋼筋應變為：ε=fy/E=360/2.0×105=1.8×10-3。

當錨桿達到此應變時，A’B段的長度為：LA’B=13.157m。

為計算方便起見，假設A點水平位移和豎向沉降分別為：δx，δy=0mm，此時，求出 δx為：

求得δx=25.2mm。即當A點變形后，在沉降為零時發生25.2mm的水平位移，錨桿應力將達到錨桿鋼筋強度設計值。

（2）AB為鋼絞線錨桿的計算

在上述變形條件下，鋼絞線應變、應力增量分別為：Δε=4.56×10-4，Δσ=88.92N/mm2。

假設錨桿變形，鋼絞線達到其強度設計值，此時的錨索應變為：ε=（fpy-σ控）/E=（1320-520）/1.95×105=4.1×10-3。

當錨索達到此應變時，A’B段的長度為：LA’B=13.187m。

為計算方便，假設A點水平位移和豎向沉降分別為：δx，δy=0mm

此時，按公式（3）求得δx=57.3mm。即當A點變形后，在沉降為零時發生57.3mm的水平位移時，鋼絞線應力將達到鋼絞線強度設計值。

同理，按上述分析方法，可計算不同位置錨桿達到其設計強度時，錨頭水平位移。圖2所示為不同參數條件下，各標高點錨桿錨頭最大水平變位（此時假設沉降為零），計算數據如表3—表5所示（注：表3—表8，錨桿參數為：錨桿與水平線夾角α=20°，錨桿最高點坡高Hi=16m，RHB400鋼筋，fy=360N/mm2，鋼絞線筋為fptk=1860N/mm2，fpy=1320N/mm2，預應力初始 σ控=520N/mm2）。

表3 巖質邊坡不同高度鋼材達到設計強度時錨桿錨頭水平位移計算數據（θ=60°）

表4 巖質邊坡不同高度鋼材達到設計強度時錨桿錨頭水平位移計算數據（θ=43°）

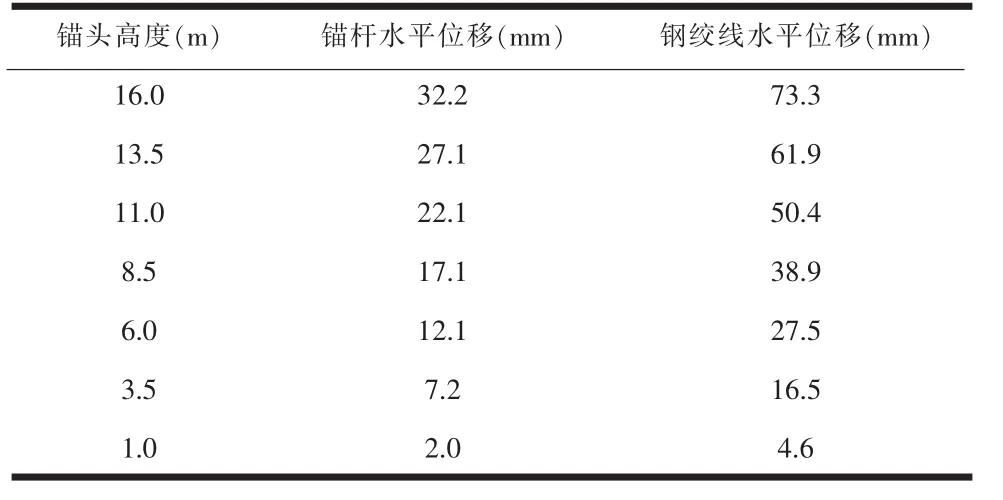
表5 巖質邊坡不同高度鋼材達到設計強度時錨桿錨頭水平位移計算數據（θ=33°）

同理，假設錨桿自由沉降變形（無水平位移），錨桿桿筋達到其設計值時的沉降變形計算結果見表6—表8。

通過表3—表5計算數據獲知：在假設巖質邊坡理論破裂面為直線時，若楔形體沿坡底（參見圖2中的D點）向外側整體傾覆（即邊坡楔形體沿D點整體向外旋轉）破壞時，錨桿可以同時達到其強度設計值，各層錨桿均可同時發揮其設計強度，故設計時坡腳應采取強錨固（或稱鎖底）措施。設計時為控制此邊坡破壞模式為整體傾覆破壞，可采取兩種方法，一是在坡腳增加錨桿（常用做法），二是在坡腳設置嵌巖地梁護腳，加強坡腳的整體性。

表6 巖質邊坡不同高度鋼材達到設計強度時錨桿錨頭垂直位移計算數據（θ=60°）

表7 巖質邊坡不同高度鋼材達到設計強度時錨桿錨頭垂直位移計算數據（θ=43°）

表8 巖質邊坡不同高度鋼材達到設計強度時錨桿錨頭垂直位移計算數據（θ=33°）

通過表6—表8計算數據獲知：在假設巖質邊坡理論破裂面為直線的條件下，若邊坡不同深度有沉降變形引起錨桿破壞時，坡頂沉降變形最大，而坡腳沉降最小。由此提示工程技術人員，上部變形監測點易觀測，但坡腳較小的沉降變形也易引發支護結構破壞，且邊坡坡腳沉降變形較小時往往被工程技術人員忽略。

按上述分析思路，同理可分析土質邊坡錨桿變形規律，限于篇幅，本文不再累述，相關工程應用及計算筆者將另文發表。

3 荷載分散型錨桿受力過程探討

《建筑邊坡工程技術規范》[1]（GB 50330—2013）無荷載分散型錨桿設計的具體規定（第8.4.1條第4款只有定性表述），而《巖土錨桿與噴射混凝土支護工程技術規范》（GB50086—2015）有荷載分散型錨桿的設計規定，荷載分散型錨桿配筋量的計算方法與普通錨桿配筋量計算方法一致。建筑邊坡工程支護設計時，設計單位一般按 《巖土錨桿與噴射混凝土支護工程技術規范》（GB50086—2015）的規定設計荷載分散型錨桿，且按其規定進行檢驗。然而，荷載分散型錨索在受力全過程中，不同階段其錨索的應力是不同的，鋼絞線變形并不協調，此點未引起設計者注意，可能產生配筋不足等問題[5-6]。下面以算例加以說明。

算例3（各單元鋼絞線應力計算）：以四單元壓力型荷載分散型預應力錨索（P錨）為例，分析不同單元鋼絞線應力變化過程。設計參數：四個單元鋼絞線自由段長度分別為：L1=20m，L2=26m，L3=32m，L4=38m，錨固段長度均為 6m。鋼絞線參 數 為 ：fptk=1860N/mm2，fpy=1320N/mm2， fpy’ =390N/mm2，E=1.95×105N/mm2，1×7 Φs15.2（為計算方便，假設每個單元均為1 束鋼絞線， 設計一般為 3～5 束），As=140mm2，σ控=500N/mm2，張拉控制應力 σ控=500N/mm2。

四個單元預拉力相等，Ni=As× σ控=140×500=70.0kN，i=1，2，3，4。

張拉時，四個單元的伸長量計算如下：

故：△L1=σ控×L1/E=500×26×103/（1.95×105）=66.7mm；

△L2=σ控×L2/E=500×32×103/（1.95×105）=82.1mm；

△L3=σ控×L3/E=500×38×103/（1.95×105）=97.4mm；

△L4=σ控×L4/E=500×44×103/（1.95×105）=112.8mm；

△L4-△L1=46.1mm；△L3-△L1=30.7mm；△L2-△L1=15.4mm。

施工時為調整四個單元的變形，其施工方法應符合文獻[2]附錄C（荷載分散型錨桿的張拉鎖定方法）或文獻[3]附錄A（補償荷載整體張拉方法）的規定。

錨具向外伸長變形時，單元1（自由段長度最短的鋼絞線）鋼絞線應力達到設計值時，錨具處向外伸長值計算如下：

△L1y=fpy×L1/E=1320×26×103/（1.95×105）=176.0mm， △L1y-△L1=176.0-66.7=109.3mm。

四個單元在一個錨具中錨固，暫不考慮其他應變不協調（如夾片類別等）問題。假設支護結構在錨具端整體向外變形，使單元1達到鋼絞線強度設計值。此時，單元2、單元3及單元4的應力值計算如下：

σ2=（500+1.95 ×105×109.3/（32 ×103）） =1166.0N/mm2（σ2/fy=88.3%）；

σ3=（500+1.95×105×109.3/（38×103）） =1060.9N/mm2（σ3/fy=80.4%）；

σ4=（500+1.95 ×105×109.3/（44 ×103）） =984.4N/mm2（σ4/fy=74.6%）；

σ1-σ2=154.0N/mm2；σ1-σ3=259.1N/mm2；σ1-σ4=335.6N/mm2。

四個錨索拉力分別為：

N1=As×σ1=140×1320=184.8kN （N1/N極=25.0%）；

N2=As×σ2=140×1166.0=163.2kN （N2/N極=22.1%，與理論值差異為-2.9%，）；

N3=As×σ3=140×1060.9=148.5kN （N3/N極=20.1%，與理論值差異為-4.9%，）；

N4=As×σ4=140×984.4=137.8kN （N4/N極=18.6%，與理論值差異為-6.4%，）

N=∑Ni=184.8+163.2+148.5+137.8=634.3kN；

N理論=∑Ni=184.8+184.8+184.8+184.8=739.2kN；

N/N理論=634.3/739.2=85.8%（只發揮了鋼絞線承載力理論值的 85.8%）。

從變形協調條件考慮，該算例鋼絞線達到設計強度時，實際承載力只發揮了理論值的85.8%（同理算得，三單元壓力分散型錨桿（其他參數不變）時，實際承載力只發揮了理論值的89.5%）。

按上述分析方法分析荷載分散型錨桿的受力全過程獲知：荷載分散型錨桿各單元鋼絞線存在應力分布不均勻現象，在破壞狀態下，單元1鋼絞線首先破壞，緊跟著其他單元隨即破壞。國家現行技術標準規定的荷載分散型錨桿配筋設計方法存在瑕疵（桿筋強度控制錨桿承載力模式），需調整相應的設計方法。調整各單元鋼絞線應力不均勻分布的方式有以下三種或三種方式的組合：①控制單元數量，荷載分散型錨桿單元數不宜超過3個；②調整各單元鋼絞線配置數量，各單元按不等量配置鋼絞線，自由段最短的單元配置數量最多，且依次減少；③調整各單元預張拉應力控制值，自由段最長的鋼絞線預應力控制值最大。

4 結語

近年來，巖土錨桿在重慶市工程建設中得到了廣泛應用，特別是由于現存土地資源的稀缺，在工程建設活動中荷載分散型巖土錨桿得到了進一步的應用。然而，在巖土錨桿應用中仍存在大量的工程實際問題和設計理論問題有待解決。本文分析指出：巖土錨桿工程設計時應首先約定所選國家現行技術標準，不宜多個技術標準同時選用，且注意不同的國家現行標準對設計要求的差異；錨桿設計應考慮變形協調問題，對以楔形體形式破壞的巖質邊坡應加強坡腳的鎖定設計，合理控制其破壞模式，不應出現剪切滑動破壞；現行國家技術標準規定的荷載分散型錨桿設計方法使各單元錨桿桿筋存在較為嚴重的應力分布不均勻現象，應引起高度重視，作者給出了調整應力分布不均勻現象的方法，可供相關工程技術人員參考。