關帝山華北落葉松林分直徑分布規律研究

秦 舟，張夢弢

(山西農業大學 林學院，山西 太谷 030801)

直徑結構作為最基本的林分結構，直接影響著林木相關因子的變化[1]。同時，為林分直徑未來生長狀態預測提供了理論依據。在林分中，直徑大小的表達形式是徑階，其大小分布在林分結構、森林調查和研制林分材種出材量表中至關重要[2-3]。所以，直徑分布模型研究對制定森林管理計劃有著很重要的意義。

林分直徑結構模型是國內外林學家關注和研究的焦點，很多學者都在研究直徑分布模型，有許多不同的理論概率密度方程都被用來描述森林的直徑分布，主要包括Weibull分布、負指數分布、正態分布、β分布、Johnson's SB函數分布、τ分布等，他們利用這些模型來預測未來林分發展狀況[3-9]。龔直文等[10]運用負指數函數在長白山對楊樺次生林(Populusdavidiana-Betulaplatyphyllasecondary forests)分析直徑分布模型。周新年等[11]運用負指數分布模型對天然林林分直徑分布進行預測，構建了具有時間序列的直徑分布預測模型，為林分生長動態的研究奠定了基礎。周國模等[12]利用Weibull分布3參數與林分特征因子間的相關關系，導出了一個改進的二元分布模型，很好地測度了浙江省毛竹(Phyllostachysheterocycla)林胸徑和年齡分布規律；夏曉波等[13]使用Weibull分布函數研究日本落葉松(Larixkaempferi)時，編制了直徑分布預估概率表；杜志等[14]以長白山地區6塊云冷杉(Piceajezoensis-Abiesnephrolepis)林樣地調查數據為基礎，采用限定混合Weibull模型方法，對直徑分布進行了模擬，發現限定混合模型是一種較好的具有高靈活性和高精度的林分直徑模擬方法；張夢弢等[15]運用3種不同的直徑結構分布模型對云冷杉混交林進行擬合發現，在3種分布模型中，負指數分布擬合近似倒J形曲線時效果較好，限定混合Weibull模型在擬合不規則直徑分布時效果較好；石振威等[16]采用Weibull分布模型擬合針櫟混交林，發現Weibull分布函數和更適于擬合針櫟全林分和櫟類(Quercusacutissima)林分的直徑分布規律。

華北落葉松(Larixgmeliniivar.principis-rupprechtii)作為華北地區的主要樹種之一，具有重要的地位，近年來以華北落葉松為對象的研究層出不窮，如溫永斌等[17]以山西太岳山華北落葉松、油松(Pinustabuliformis)林分為對象，運用相關模型對該地區森林生態系統的碳水循環相互作用進行深入研究；李慧婷[18]以青海華北落葉松為對象，對其直徑分布和樹干材積模型進行擬合，表明β分布及Richards模型分別在擬合直徑分布和樹干材積方面效果較好；僅有的直徑分布研究如周澤宇等[19]以線性混合效應模型擬合華北落葉松直徑分布結果表明，塞罕壩華北落葉松人工林直徑分布最優模型為Weibull分布。但是上述研究對于不同狀態下林分直徑結構不同分布狀態擬合相對較少。本研究以龐泉溝自然保護區華北落葉松林分為對象，通過對林分直徑結構進行擬合，了解此時林分直徑分布狀態，為今后林分直徑分布的調查提供捷徑，較全面地了解林分生長動態，為林分撫育間伐技術的確定和實施，以及林分結構的調整提供一定的技術支持和理論依據。

1 材料與方法

1.1 研究區概況

研究地選擇在關帝山龐泉溝自然保護區，位于山西省交城縣西北部和方山縣東北部交界處，地處呂梁山脈的中部，111°22′-111°33′E，37°45′-37°55′N，海拔1 800～2 830 m，保護區南北長15 km，東西寬14.5 km，總面積10 443.5 hm2，森林覆蓋率達85%[20]。保護區地處暖溫帶大陸性季風氣候區，年平均氣溫4.3℃，極端最高氣溫32℃，極端最低氣溫-26.1℃，7月平均溫度18℃，1月平均溫度-12.4℃。大部分地區≥10℃的積溫1 800℃～2 950℃。無霜期100～125 d。年平均降水量822.6 mm。龐泉溝自然保護區是山西森林面積及森林蓄積量最大的自然保護區，層次復雜、結構完整、樹種豐富。植被具有明顯的垂直帶譜，海拔1 800 m以下主要以溫性灌叢、落葉闊葉林、溫性針葉林和溫性針闊葉混交林為主；1 800 m以上區域主要以寒溫性針葉林和亞高山灌叢草甸為主[21]。主要樹種有油松、蒙古櫟(Quercusmongolica)、山楊、白樺、華北落葉松、側柏(Platycladusorientalis)、云杉(Piceaasperata)等。

1.2 樣地概況

2017年在龐泉溝自然保護區內的八道溝和臥牛坪地區，在實地踏查的前提下，選擇林相較好、具有代表性的地塊布設9塊0.09 hm2(30 m×30 m)的樣地，對樣地中立木進行每木檢尺，實測胸徑、樹高、冠幅、坐標等基本調查因子，并對每株立木進行樹種鑒定(表1)。由于選取樣地面積較小，樣地上林木株數少，研究采用每4 cm徑階為1個徑階進行劃分，并將所得數據統計進表。由表1可知，選取的9塊樣地之間林木株數差距很大，林木最多的5號樣地達到了90株，而最少的3號樣地僅有37株。平均胸徑最小的是7號樣地，為21.6 cm，最大的是4號樣地，為30.1 cm，各樣地之間差距較大。大部分樣地直徑分布范圍不大，變動系數>0.45的樣地僅有3號、8號和9號樣地。

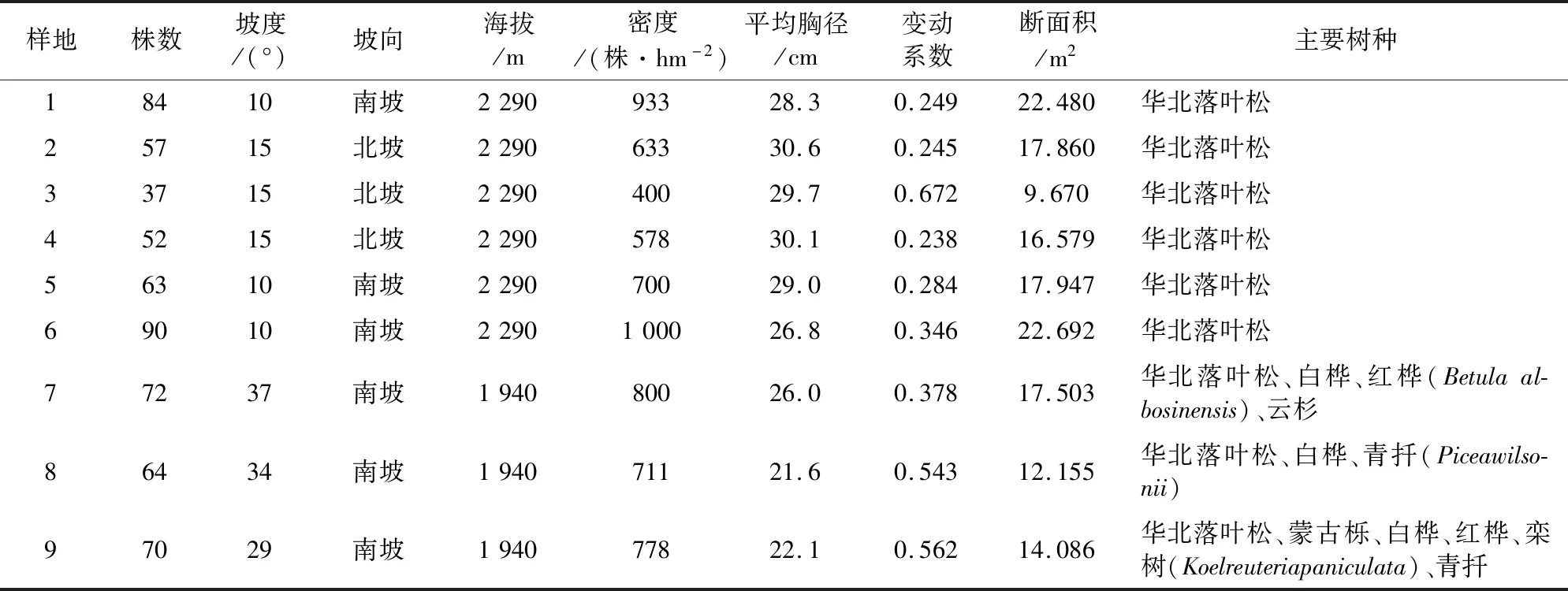
表1 關帝山華北落葉松林分概況Table 1 General situations of L.gmelinii var.principis-rupprechtii forest in Guandi Mountain

1.2 研究方法

1.2.1 Weibull分布 Weibull分布具有求解方法多樣、求解簡單的優點，無論是在同齡林還是異齡林或者其他類型的林分結構研究中均取得了很好的擬合效果[22-23]。

Weibull分布計算公式：

(1)

式中,a為位置參數，也就是直徑分布最小徑階下限值；b為尺度參數、c是形狀參數、e為自然對數的底，x為對應的徑階直徑，f(x)為對應各徑階的株數百分比[24]。

1.2.2 負指數分布 未受干擾的天然異齡林趨于一個可用指數方程表達的直徑分布[10]。負指數分布計算公式為：

f(x)=ae-bxx≥0,b>1

(2)

式中:x為胸徑;a、b表示直徑分布特征的常數,其中,b表示林木株數在連續的徑階中減小的速率,a為林分相對密度[10]。

1.2.3 限定混合Weibull分布 限定混合模型的公式為[13]：

(3)

式中,可看作k個三參數Weibull模型組成的，由于本研究僅考慮2～3組分的限定混合情況，其擬合情況分別表現為雙峰和三峰，因此原式分別可表達為

雙峰Weibull模型：

f(x)=ρ1f1(x)+ρ2f2(x),ρ1+ρ2=1

(4)

三峰Weibull模型：

f(x)=ρ1f1(x)+ρ2f2(x)+ρ3f3(x),ρ1+ρ2+ρ3=1

(5)

式中,ρi表示第i個組分所占比例，0≤ρi≤1且；∑ρi=1;fi(x)表示第i個概率密度函數，每個概率函數都有不同的平均值、方差。用ai、bi、ci(i≤3)來分別表示位置、尺度和形狀參數，并通過R語言的mixdist包完成參數的計算[15]。

1.2.4 檢驗方法 使用偏差(Rias)和均方根誤差(Rmse)檢驗3種模型的擬合效果，并進行卡方檢驗測量模型的擬合度。

(6)

(7)

(8)

式中，Ni為該徑階實測值； 為該徑階模型擬合值；m為徑階數；χ2的自由度為(m-k-1)，其中k為參數值。

2 結果與分析

2.1 直徑分布擬合

表2樣地3中3參數模型形狀參數c=5.780，模型擬合曲線呈現右偏分布除此之外均為正偏山狀。在限定混合Weibull模型中，只有6號樣地為3部分組成，其余均由2個組分組成，而且由于6號樣地第3個組分的形狀參數c3值為12.993，使得分布曲線向左偏移。其余2組分的混合分布模型中，第1組分直徑分布為正偏山狀，在第2組分中形狀參數c2值只有5號和8號樣地是正偏山狀分布，其余均為左偏態分布。

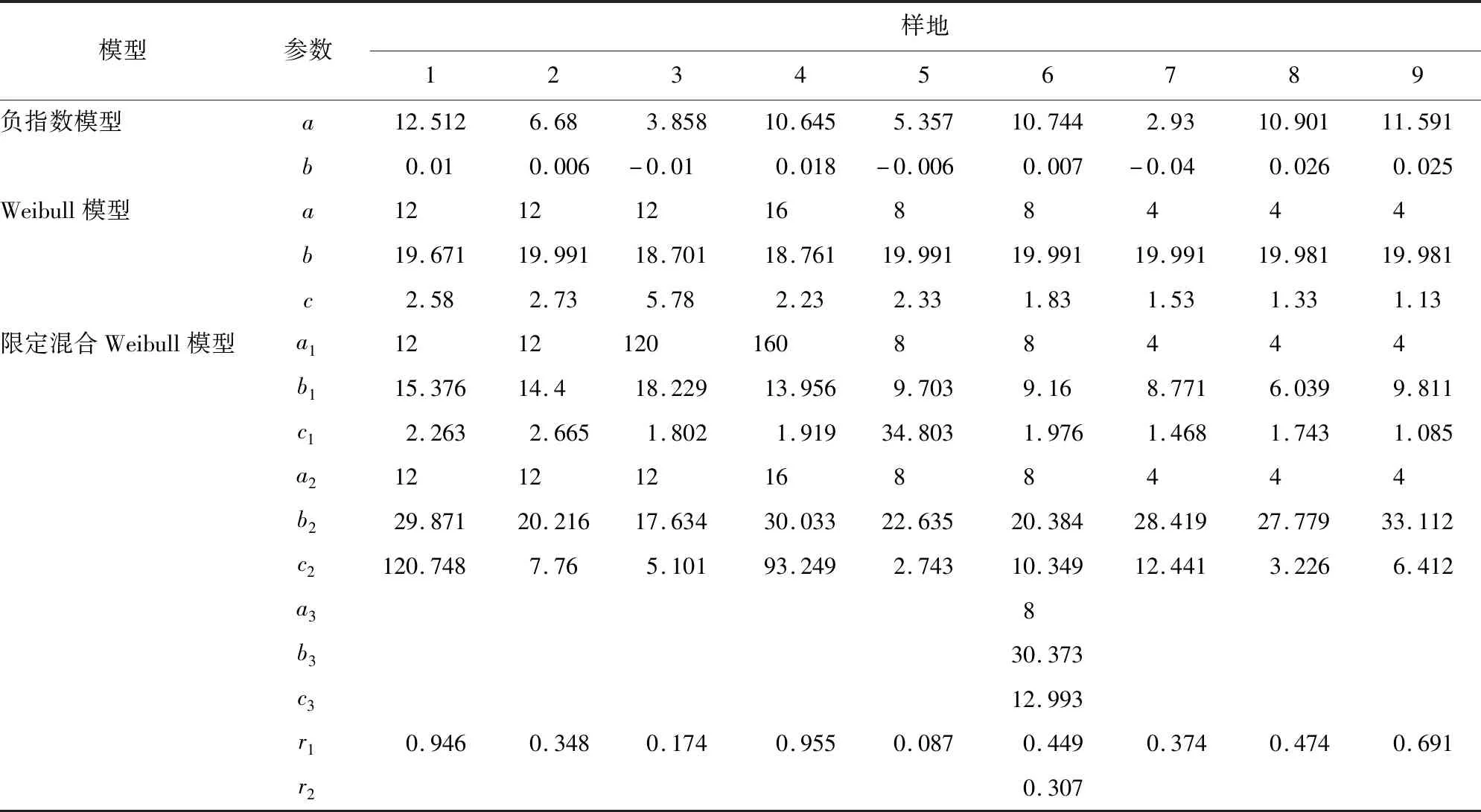
表2 關帝山華北落葉松林3種直徑分布模型的參數Table 2 Parameters of three diameter distribution models of L.gmelinii var.principis-rupprechtii forest in Guandi Mountain

圖1為各樣地直徑分布直方圖和3種分布函數的擬合曲線，1號、2號和4號樣地符合正態分布，3參數Weibull模型擬合效果較好；3號樣地呈現明顯的單峰曲線，峰值在30 cm處，3參數和限定混合模型擬合精度較好；5號樣地也呈現出近似雙峰分布的曲線，峰值為18 cm和26 cm；7號樣地為近似雙峰分布曲線，峰值分別為14 cm和34 cm；對于5號樣地和7號樣地，限定混合模型擬合效果優于其他模型；6號樣地呈現類似3峰分布曲線的，也同樣是限定混合Weibull分布模型擬合效果好；8號樣地和9號樣地在圖中顯示近似反J型曲線，負指數模型呈現的效果更好。

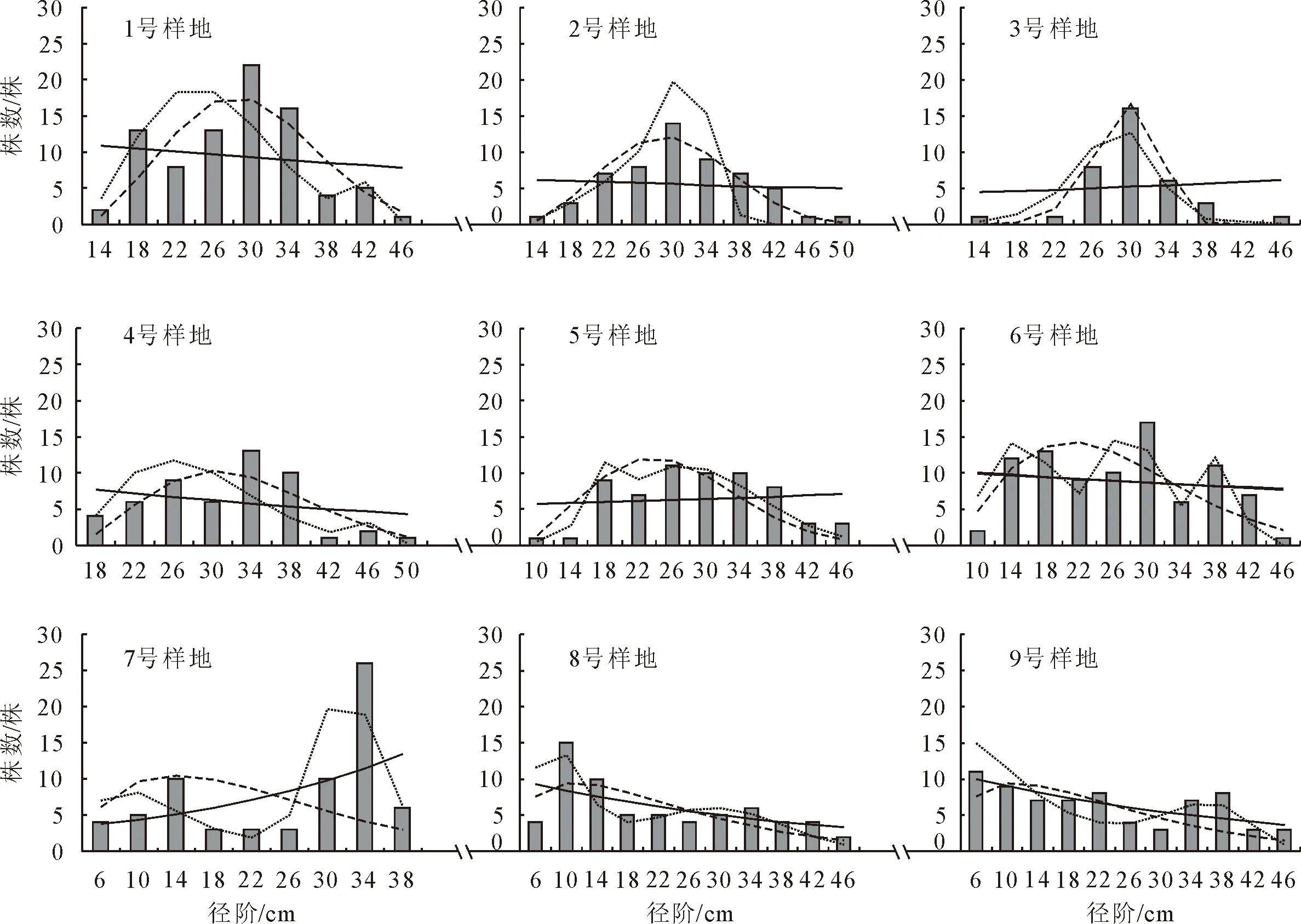
圖1 關帝山華北落葉松林9塊樣地3種直徑分布模型的擬合效果Fig.1 Fitting effect of three diameter distribution models for 9 sample plots of L.gmelinii var.principis-rupprechtii in Guandi Mountain

2.1 擬合檢驗

表3利用均方根誤差(rmse)、平均偏差(bias)和χ2值以及P值對所得樣地數據進行檢驗。同一樣地上，不同直徑分布模型的平均偏差和χ2越小且P值越大的話，則該直徑分布模型擬合效果越準確。例如2號樣地上3參數模型擬合效果最好，因為該模型的P值最大且平均偏差和χ2最小，同理1號和4號樣地也均是3參數模型為最優擬合效果。而8、9號樣地呈現較明顯的反J型曲線，平均偏差與χ2值也反映負指數分布模型的擬合精度更高。3號樣地上負指數模型與限定混合模型P值相差不大，但后者的平均偏差和χ2值比前者小，故3號樣地上限定混合模型精度較高。其余樣地上限定混合Weibull模型的P值遠大于其他模型，所以擬合精度高于其他模型。

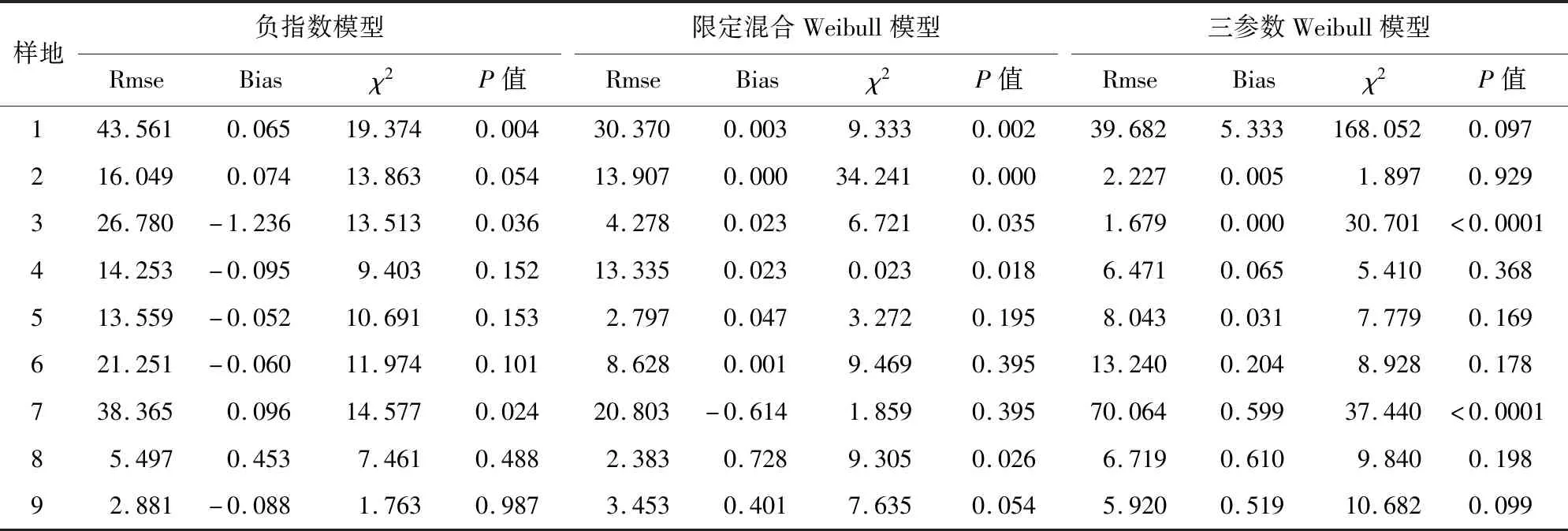
表3 關帝山華北落葉松林3種直徑分布模型的檢驗結果Table 3 Test results of three diameter distribution models of L.gmelinii var.principis-rupprechtii in Guandi Mountain

圖2較為直觀地反映出1號樣地中各模型的殘差在初始和中間徑級波動劇烈，呈現出交替波動的現象，并且隨著徑級的增大，3種模型殘差的波動幅度逐漸降低。2號和3號樣地的3參數Weibull模型在樣地上所有徑級內的殘差波動都較小。4號樣地3種模型在前幾個徑級內殘差波動不大，在后幾個徑級內殘差先增后減。6號樣地內限定混合模型殘差除第1個徑級外,整體波動不大，而7號樣地上3種模型則隨著徑級的增大,殘差波動幅度也越來越大。5號樣地3種直徑分布模型殘差波動比較穩定,整體上變化幅度不大。9號樣地全徑級上3種直徑分布模型殘差值均較低,而8號樣地除前幾個徑級外,3種模型殘差值也跟9號樣地情況類似。

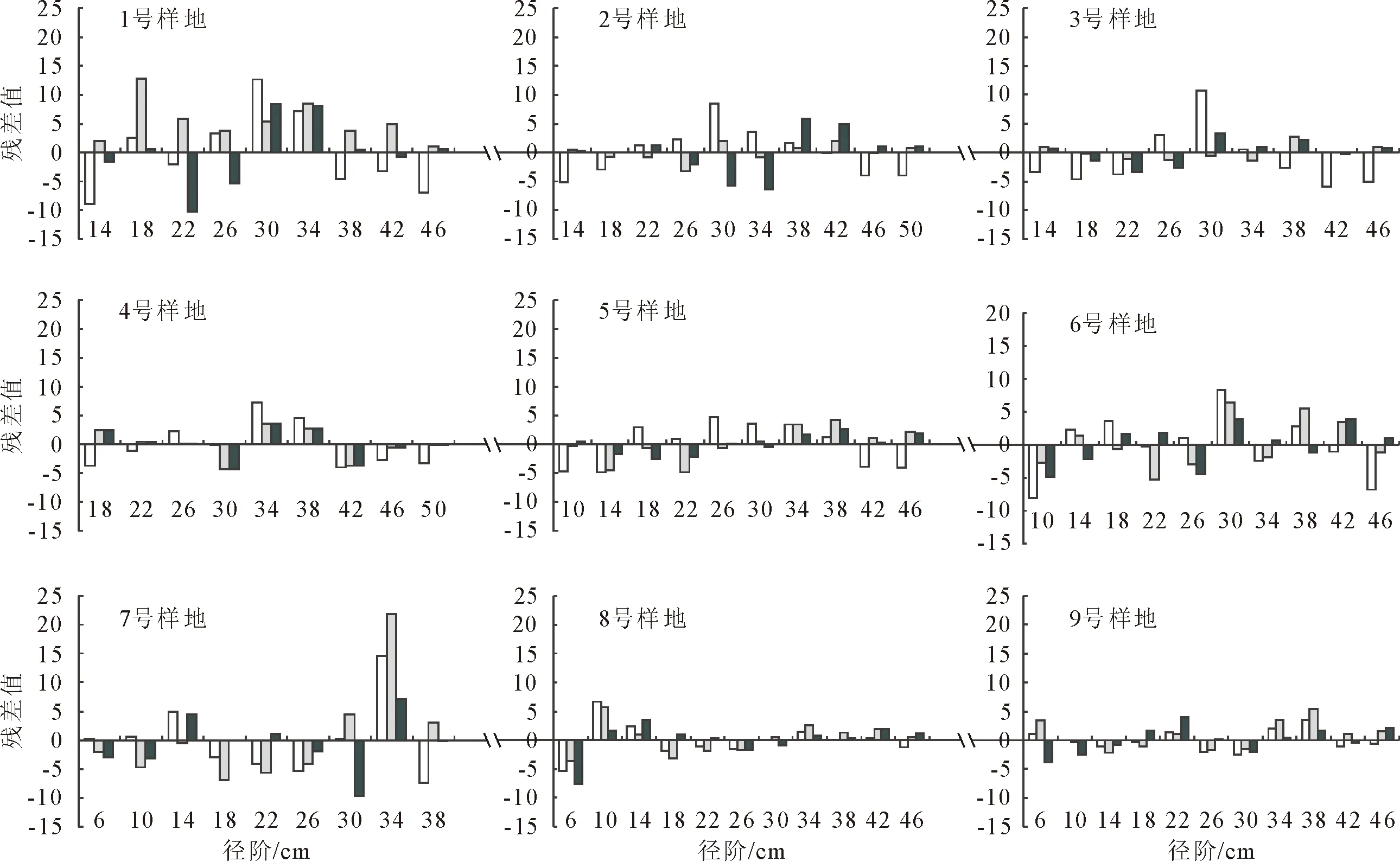
圖2 關帝山華北落葉松林9塊樣地3種直徑分布模型擬合結果的殘差值Fig.2 Residuals of fitting results of three diameter distribution models for 9 sample plots of L.gmelinii var.principis-rupprechtii in Guandi Mountain

3 結論與討論

在森林經營中，直徑分布擬合模型要求高精度和高靈活性，合理運用不同的模型以及非參數方法不可或缺。本研究采用3種模型進行模擬比較，在不同樣地內各模型的擬合效果各不相同。研究分析發現3種不同直徑分布模型分別有其各自的最適用環境。若林地上林木株數隨徑級的增大而逐漸減少，呈現反J型分布時，負指數直徑分布模型能夠更好的擬合林木在各徑級上的分布情況，該模型可為幼齡林的撫育采伐提供合理的依據。Weibull直徑分布模型對于明顯單峰山狀分布的人工林分，預測結果更準確可靠。而對于呈現不規則多峰山狀的林分,限定混合模型的擬合效果更好。在反J型分布曲線的樣地上負指數模型擬合效果更好，單峰分布的情況更適用Weibull模型和限定混合模型，而限定混合Weibull模型在擬合雙峰及多峰型直徑分布林分時的精度更高。1～6號樣地為華北落葉松純林，其中1號、2號和4號樣地呈現出正態分布，試驗表明該林分直徑結構相對單一，為同齡純林；3號、5號和6號樣地呈不對稱單峰或多峰曲線，為次生異齡林；7～9號樣地為混交林，7號樣地為近似雙峰曲線，8號和9號樣地呈現反J型曲線，直徑結構相對復雜，這與異齡混交林的規律相一致，這種狀態下該林分能夠維持天然更新，且大徑階林木保持一定數量，表明該生態系統穩定性較好[25]。

由于選擇樣地面積較小，因此在劃分林分徑級時采用生產上常用的4 cm劃分法。在測量過程中，由于小徑階的林木過少，造成模型擬合中各樣地起測徑階不同，造成了模型的擬合精度與評價有一些影響。小徑階林木過少可能是因為人為的頻繁干擾所致。因此，我們在減少對林木破壞的同時，要保護林下天然更新，或者進行人工林下補植等，保證天然林的健康更新機制[15]。

本試驗通過對3種直徑分布模型的擬合發現，純林林分樣地的峰值多出現在30 cm左右徑階處，混交林的峰值則多出現在小徑階，應采用不同措施對該林分進行適度調整。若林分為幼齡林或中齡林，采用封育措施；若林分為成熟林，則選擇進行適度擇伐；若大徑階林木過多時，對該徑階的林木進行適度采伐。

利用直徑分布模型分析林分結構，可為林分經營提供依據和措施，從而提高林分結構的多樣性[26]。本次研究收集關帝山華北落葉松純林和混交林地的數據，運用3種模型對該地林分進行擬合，結果表明該地林分相對合理，但也需要進行一定的調整，從而改善該地林分的經濟和生態效益。下一步研究重點是通過及時復測及收集信息，得到樣地林分直徑的平均狀態，以期更好地提高該地區華北落葉松的直徑結構擬合精度。根據不同調查期內數據變化，分析該地區林分結構動態變化。同時，利用該樣地林分的直徑結構模型，規劃和調整該地區現有林的結構，加快森林群落結構的恢復速度，促進該地區林分健康發展。