毛竹林竹鞭生長特征和空間結構的探地雷達無損探測*

熊雨露 周宇峰 李平衡 童 亮 周國模 施擁軍 杜華強

(浙江農林大學省部共建亞熱帶森林培育國家重點實驗室 浙江省森林生態系統碳循環與固碳減排重點實驗室 浙江農林大學環境與資源學院 杭州 311300)

毛竹(Phyllostachysedulis)林地下竹鞭系統是由同一母竹發出的、各年齡竹鞭相互聯結的組合(蔡偉國， 1986)。地下竹鞭系統在毛竹林生態系統中扮演著重要角色，它可在毛竹生長發育過程中獲取水分和營養，也是支撐和固定立竹的重要器官； 竹鞭在毛竹林高效固碳過程中具有重要貢獻，研究表明竹鞭系統的碳存儲量約占毛竹林總碳量的40%(周國模， 2006)； 更為重要和特殊的是，竹鞭把竹林中各單株竹子連接起來，使竹子個體之間(老竹與新竹、老竹與老竹)發生著極復雜的物質和能量交換，從而實現毛竹林“爆發式生長”等高效固碳特性。深入研究毛竹林竹鞭空間結構及動態變化，是詮釋毛竹林高效固碳機理過程的關鍵。

由于毛竹林竹鞭深入地下，觀測不便，很難精確調查，導致自然條件下的竹鞭研究無論在廣度和深度上均落后于地上部分(王燕等， 2008; 周本智等， 2004)。傳統的竹鞭探測方法(挖根法、土壤剖面法等)雖能提供合理且精確的信息，但費時費力，還會破壞土壤環境和毛竹竹鞭，從而無法長期和重復性觀測研究(周本智等， 2004)。近年來，國內外科學家發展了一系列無損根系探測方法，其中探地雷達(ground penetrating radar，GPR)是一種快速且可重復觀測的地球物理技術，它利用電磁波在媒質電磁特性不連續處產生的反射和散射實現淺層成像、定位，進而實現對地表下目標的探測(Raz-Yaseefetal., 2014)。由于特有優勢，GPR應用于根系探測的潛力巨大。目前主要應用于樹木根系的根徑大小和根系生物量估算等方面(Bassuketal., 2011; Butnoretal., 2012; 崔喜紅等， 2011)。把GPR應用于毛竹林竹鞭結構的探測至今未見報道，為此，本研究基于GPR探測毛竹林竹鞭生長特征和空間結構，以期為毛竹林地下竹鞭研究提供新思路。

1 研究區概況

研究區位于浙江省杭州市臨安區浙江農林大學平山實驗基地(118°51′E，29°56′N)，該區屬季風性氣候，溫暖濕潤，光照充足，雨量充沛，四季分明。年均降水量1 613.9 mm，年均氣溫16.4 ℃，年均日照時間1 847.3 h，全年無霜期237天。樣地內土壤屬黃壤土，土層較厚，土壤濕潤和疏松透氣較好，石礫含量約10.90%。

2 研究方法

2.1 樣地設置

選取3塊無人為干擾的5 m×5 m毛竹林樣地，樣地毛竹密度4 800株·hm-2，平均胸徑9.21 cm，林下伴生有稀疏草本和灌木。

2.2 雷達探測與數據采集

圖1 樣地測線布設情況(左上)、竹鞭挖掘情況(左下)和測線與毛竹位置示意(右)Fig.1 Layout of surveying lines in sample plot (left-upper),the excavation of bamboo rhizomes in sample plot (left lower),and the measurement lines and P. edulis positions (right)

2.3 竹鞭實地挖掘與測定

對經探地雷達掃描后的毛竹林樣地，先進行每木檢尺，記錄胸徑和年齡因子，然后挖掘樣地內竹鞭，在不破壞竹鞭的基礎上沿竹鞭兩側挖掘，并清除竹鞭附近的泥土，使鞭體能裸露出。隨后使用全站儀，記錄各條竹鞭的三維坐標信息。3塊樣地分別有完整竹鞭23、26和21條，根據竹鞭年齡識別特征，將完整的幼、壯、老齡竹鞭現場編號后帶回實驗室進一步處理。

2.4 竹鞭樣本處理與測定

將竹鞭樣品上附著的土壤及石塊等雜質去除并置于實驗臺上，使用皮尺測量鞭長； 之后沿竹鞭每隔10 cm進行標記，用游標卡尺于標記處的上下左右方向分別測量3次，控制誤差在1 mm以內，取測量結果均值為該部位直徑，取測量結果的總體均值作為該樣品直徑(Cuietal., 2013)。將竹鞭樣品沿標記處分割成小段，以方便使用分析天平進行鮮質量測定。將全部樣品測定鮮質量后放入烘箱，先105 ℃殺青30 min，之后80 ℃烘干至恒質量，測得干質量。

2.5 雷達數據預處理與竹鞭信號提取

原始雷達圖像很難提供足夠的要探測目標地物的幾何信息，在獲取雷達數據剖面時，原始回波信號中不僅包含有目標信號，還包括收發天線之間的直接耦合波和地面反射波以及其他干擾信號等，所以雷達接收到的回波實際是一種弱信噪比、波形畸變的信號，這些都給雷達剖面的解譯帶來困難。因此，在進行解譯之前，必須對原始雷達采集數據進行雜波處理和調整。預處理的目的是去除或盡可能地降低干擾信號成分，提高數據的信噪比，并對接收回波進行波形修正，具體需要進行初至時間拾取、系統溫漂誤差校正、背景雜波去除、信號增強和偏移歸位處理5步預處理，在GprMax軟件中完成，具體處理方法和步驟參考該軟件的用戶手冊。圖2為本試驗數據的5個預處理過程，其中字母a～e分別是經過了去直流漂移、靜校正、抽取平均道、巴特沃斯帶通濾波和滑動平均這5步處理后的竹鞭雷達數據圖。根據樣地內所有掃描的雷達測線中提取的竹鞭信號所在位置與土層深度，得到樣地內竹鞭的垂直與水平分布。

圖2 探地雷達數據預處理過程Fig.2 Preprocessing of ground penetrating radar data

2.6 基于雙曲線模型的竹鞭直徑估計

按Ristic等(2009)提出的雙曲線模型方法來估算竹鞭直徑。根據探地雷達電磁波的傳播原理，當地下目標為圓柱體時，會有如圖3所示的回波雙曲線模型。其中圓柱體目標物跟天線以及電磁波的傳播距離滿足勾股定理：

(ri+R)2=(xi-x0)+(r0+R)2。

(1)

式中：R為目標物的半徑(cm)；xi為天線的初始位置(cm)；x0為天線經過時間t移動到目標物正上方的位置(cm)；ri為初始時天線和目標物之間的距離(cm)；r0為經過時間t天線和目標物之間的距離(cm)。由于電磁波從發射到接收走了往返兩趟距離，所以ri=vti/2，r0=vt0/2,ti為天線位于xi時探測目標物電磁波的傳播時間(s),t0為天線位于x0時探測目標物電磁波傳播時間(s)。公式 (1) 可以通過R、v、x0和t0這4個參數的關系式來表示，將其展開并整理如下：

(2)

根據公式(2)可知，雙曲線模型擬合需估計x0、t0、v和R這4個參數，這就把直徑估算轉化為雙曲線擬合問題。雙曲線擬合所需的數據(x,t)由雷達掃描得到，可利用雷達配套的reflexw軟件來拾取； GprMax正演得到的數據需要通過Matlab編寫程序進行拾取，具體方法如下： 在得到模型二維剖面圖像后，使用ginput函數設置需要拾取的采樣點個數，然后在雙曲線上選取需要的坐標數據，數據類型為(xi，ti)。由于橫坐標數據太小，所以需進行放大，將橫坐標單位由m轉化為cm。

4個待擬合參數中的x0和t0是雙曲線的頂點，較易確定。研究目標是準確估計直徑R，而波速v是未知數，錯誤的v取值容易導致錯誤的R擬合值。因此需先限定波速v的合理取值區間，從而得到精度較高的R估計值。根據試驗結果及Ristic等(2009)文獻中的結論，波速的最小值和最大值相差較小，例如直徑10～80 mm物體的波速為5.53×107～6.68×107m·s-1。因此限定波速v的范圍為[5.53×107, 6.68×107]； 然后進行雙曲線模型擬合，擬合確定直徑R。

2.7 竹鞭生物量擬合模型

竹鞭生物量即竹鞭的干質量(WD)。如將竹鞭的某段假設為圓柱體，那么當假設竹鞭直徑為D、長度為L、密度為δ時，竹鞭生物量可簡單表示為WD=1/4πD2Lδ，但實際情況并非如此，竹鞭形狀不規則及竹鞭節間生長濃密細根都會影響生物量估算精度。因此需合理選擇竹鞭生物量模型。

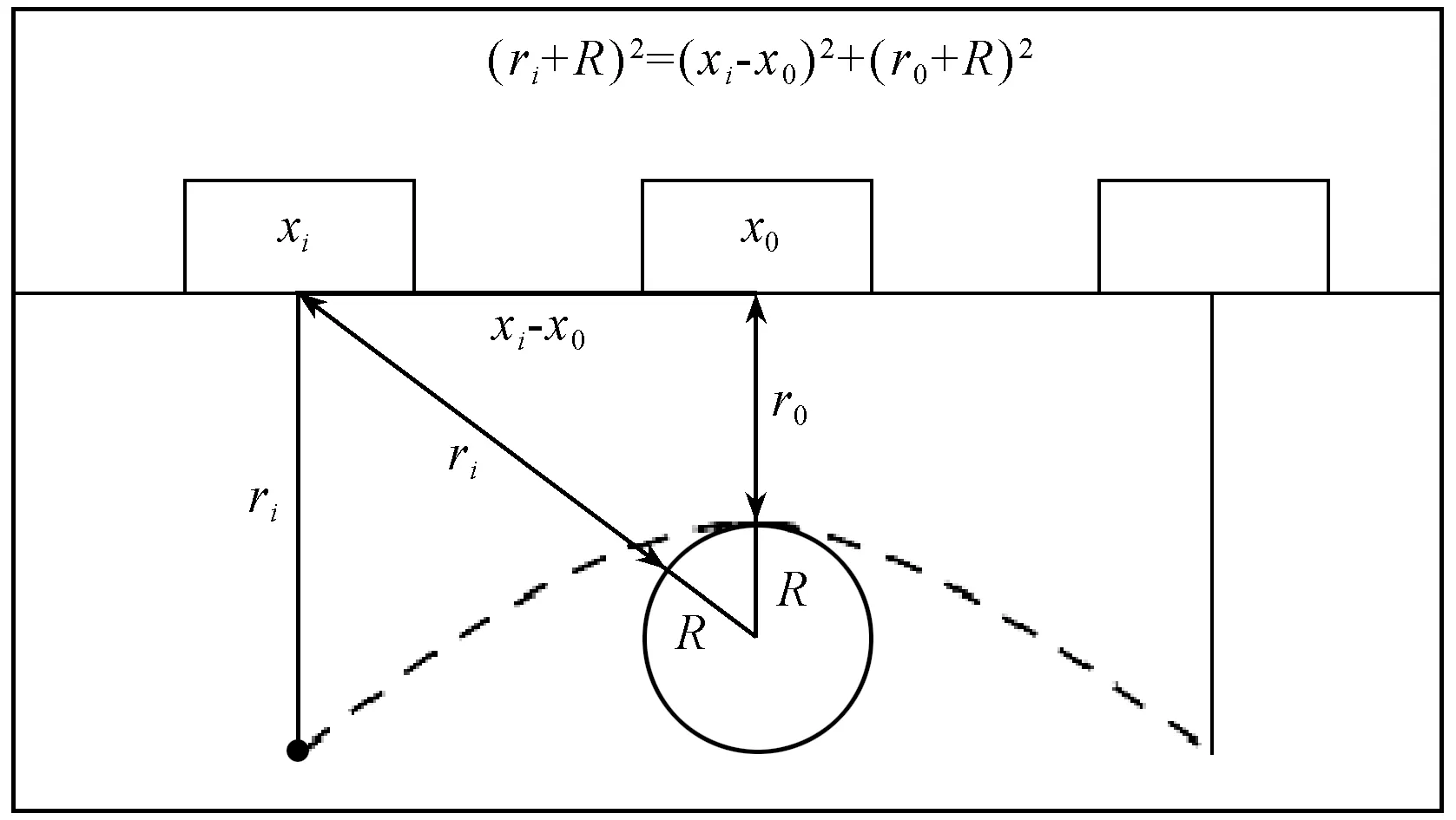
圖3 雙曲線模型原理Fig.3 Principle of hyperbolic model

各樹種和毛竹的生物量模型種類有很多，概括起來有3類(胥輝， 1998; 曾偉生， 2011)： 冪函數模型、多項式模型和指數函數模型。借鑒立木生物量模型變量的選擇，結合探地雷達容易獲取的竹鞭信息，本研究構建竹鞭生物量模型時，采用的變量包括鞭長L、鞭徑D及DL和D2L，并使用冪函數模型、多項式模型和指數函數模型：

BR=aDb；

(3)

BR=a(DL)b；

(4)

BR=a(D2L)b；

(5)

BR=a+bD+cD2；

(6)

BR=a+bDL+c(DL)2；

(7)

BR=a+bD2L+c(D2L)2；

(8)

BR=aebD；

(9)

BR=aebD2；

(10)

BR=aebDL；

(11)

BR=aebD2L。

(12)

式中： BR為竹鞭生物量；a,b,c為參數。

2.8 模型檢驗

為驗證竹鞭直徑模型的估計精度，隨機選取10條竹鞭的雷達數據，利用雙曲線模型估計其直徑，并通過這10條竹鞭的實測直徑值，計算模型估計直徑的相對誤差來檢驗直徑模型的估計精度。

為驗證竹鞭長度和空間位置(平面位置與深度)的探測精度，隨機選取10條竹鞭，提取雷達數據計算每條竹鞭的長度，每條竹鞭等距離分為10段，選取每段中點的空間位置(X，Y，Z)用于檢驗所探測竹鞭空間位置的精度。長度和空間位置精度評價采用估計值與實測值的相對誤差這一指標。

對于竹鞭生物量擬合模型，隨機選取18條竹鞭作為建模樣本，另外選5條竹鞭作為模型檢驗樣本。模型建立精度與模型檢驗精度評價都采用確定系數(R2)和均方根誤差(RMSE)這2個指標。

3 結果與分析

3.1 竹鞭直徑估計

使用基于雙曲線模型估算的10條竹鞭直徑結果見表1。總體而言，竹鞭直徑估算值和實測值較接近，誤差范圍為-14.45%～20.66%，估算效果很好(圖4)，說明該直徑模型估算有效。

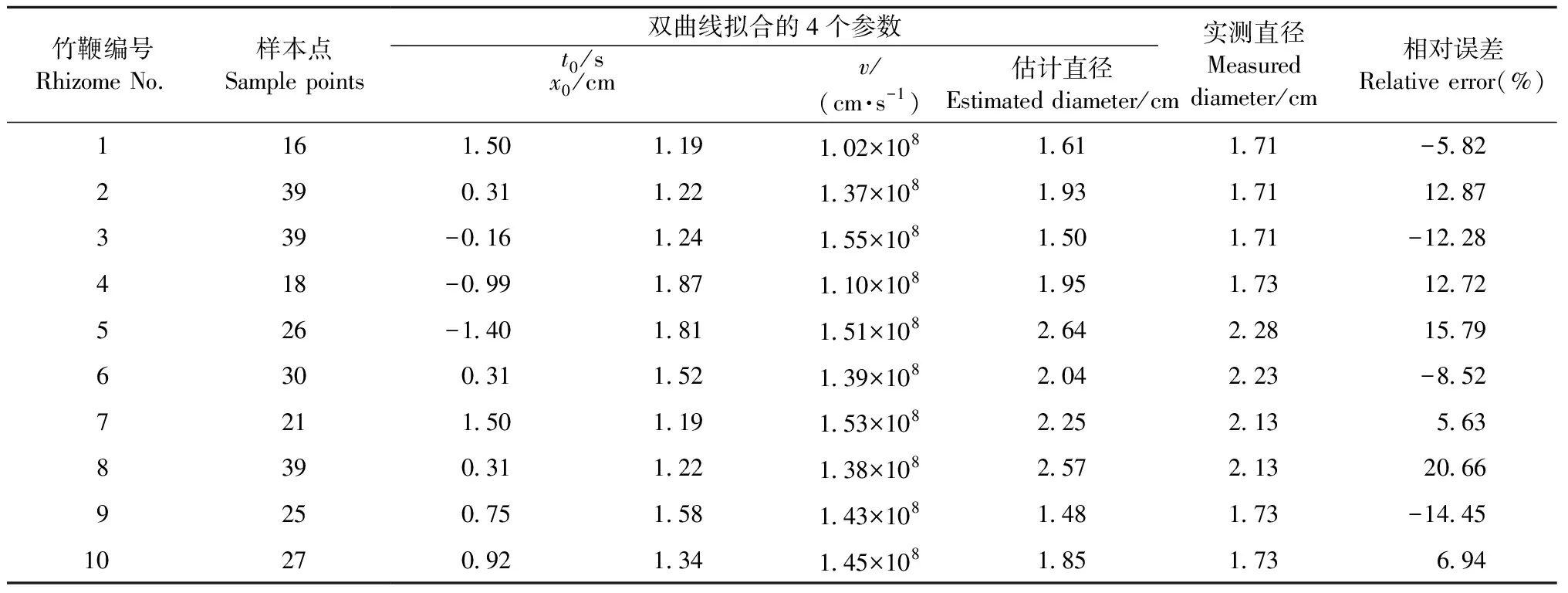
表1 基于雙曲線模型的竹鞭直徑估計結果Tab.1 Estimation of bamboo rhizomes diameter based on hyperbolic model

3.2 竹鞭空間結構特征

根據雷達掃描數據提取竹鞭空間位置信息，并估算其直徑和生物量，再按垂直分布和水平分布來分析其空間結構特征。下面以樣地I (有23條竹鞭) 為例來分析竹鞭的垂直與水平分布特征，另外2塊樣地的結果類似，不再重復。

3.2.1 垂直分布特征 表2為樣地I內所有竹鞭在4個土層的分布情況統計表。竹鞭數量的土層分布為： 0～5 cm(裸露)土層5條、5～20 cm土層9條、20～40 cm土層7條、>40 cm土層2條，說明竹鞭集中分布于0～40 cm土層，占竹鞭條數總量的91%，竹鞭的鞭長和生物量分別占總量的95%和93%。竹鞭直徑分布范圍為1.88～3.21 cm，4個土層的平均直徑分別是2.02、2.01、2.36和2.42 cm，變化不大，但竹鞭直徑在下層土壤(20～40 cm和>40 cm)明顯大于上層土壤(0～5和5～20 cm)。樣地內的總鞭長和生物量分別為135.2 m和2.5 kg，折合為54 080 m·hm-2和1 001.17 kg·hm-2，即竹鞭總長度與地上竹稈總長度(竹稈平均高×株數)相當，但由于竹鞭直徑(平均2.15 cm)遠小于竹稈胸徑(平均9.2 cm)，使竹鞭總生物量要遠低于竹稈。

3.2.2 水平分布特征 根據雷達掃描數據提取樣地內竹鞭的空間位置信息，在忽略竹鞭的土層深度分布以后，得到竹鞭的水平分布(圖5)。圖5表明竹鞭在地下走勢較曲折，空間分布相對均勻。同一竹鞭的直徑差異不顯著(P>0.5)，但不同竹鞭差異顯著(P<0.01)。不同竹鞭的長度也差異較大，由于樣地大小限制，有些竹鞭延伸到樣地外，導致部分竹鞭不完整。同時，結合地上立竹位置可清楚看出哪些立竹屬于同一竹鞭系統。從圖中還可看出，不能依據立竹之間距離來判斷是否為同一竹鞭相連，因為有些立竹空間位置很近卻不屬于同一竹鞭，有些立竹空間位置較遠卻由同一竹鞭相連。

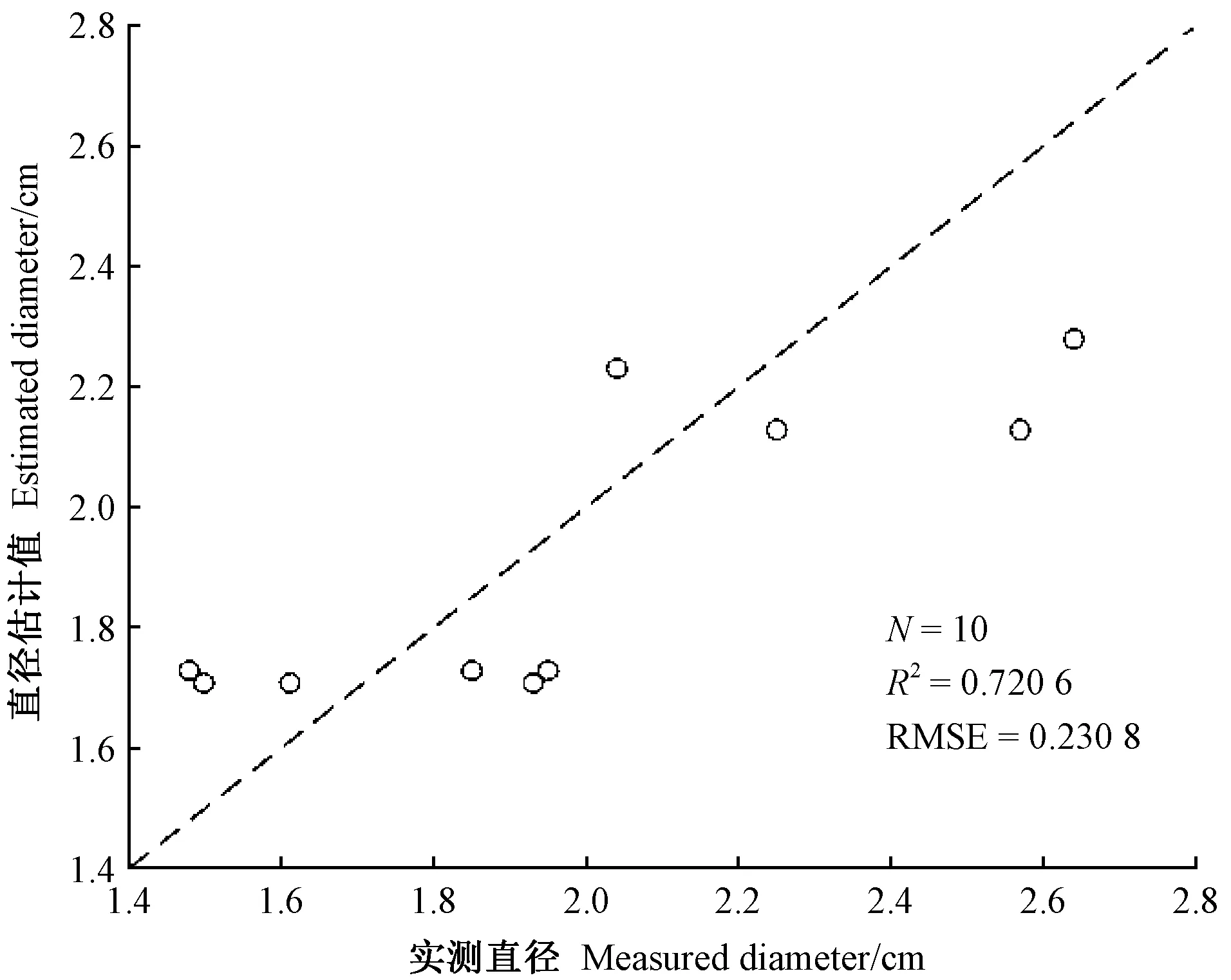
圖4 實測直徑與估計直徑的對比 Fig.4 Comparison of measured diameter with estimated diameter

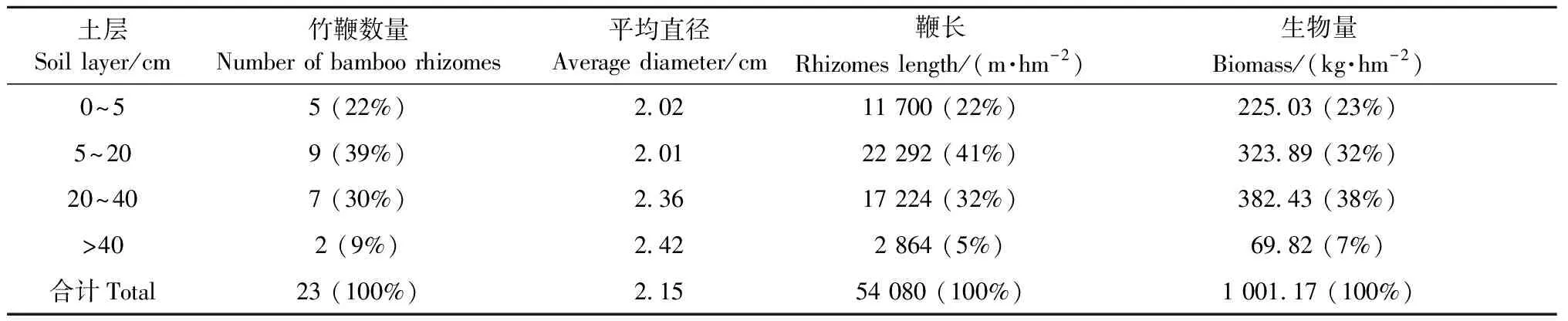
表2 竹鞭在不同土層中的分布特征Tab.2 Characteristics of bamboo rhizomes in different soil layers

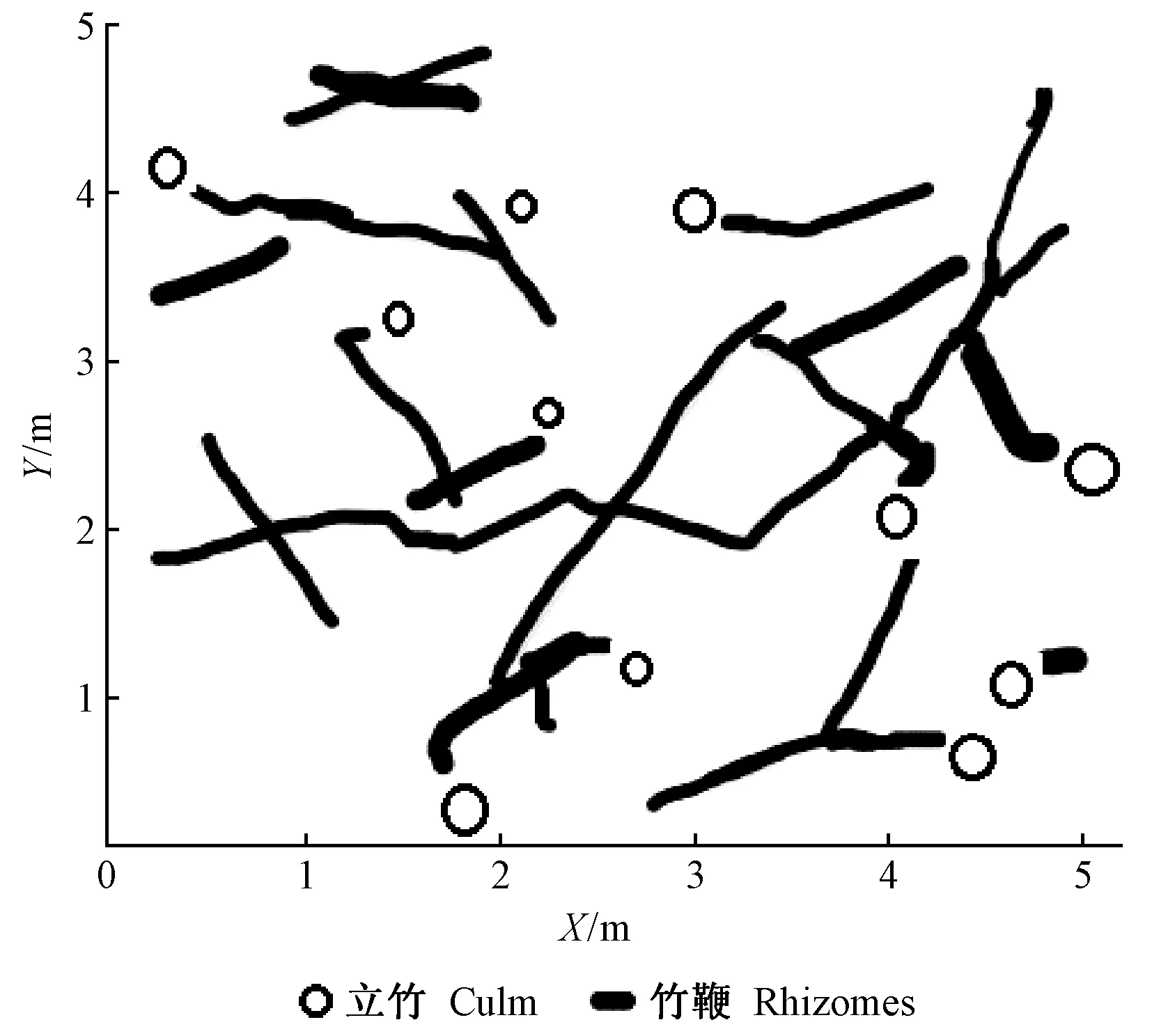
圖5 樣地竹鞭水平分布Fig.5 Horizontal distribution of plot bamboo rhizomes

3.2.3 竹鞭長度與空間位置探測精度的檢驗 表3為樣地內10條竹鞭的長度與空間位置探測精度的檢驗結果。探地雷達探測竹鞭長度的相對誤差為0.53%～8.51%，空間位置X、Y、Z方向上的相對誤差分別為0.13%～6.65%、1.23%～6.55%和2.42%～7.41%。竹鞭長度和空間位置的探測精度遠大于竹鞭直徑的估計精度，這是因為竹鞭長度一般達到1 m以上，誤差相對較小； 空間位置也較好確定，誤差較少； 而直徑只有2～3 cm，誤差相對較大。對竹鞭直徑的估計精度是探地雷達應用的重要方面，也是造成竹鞭生物量估算精度誤差的主要原因。

3.3 竹鞭生物量估計

3.3.1 竹鞭生物量模型的構建與檢驗 10個竹鞭生物量模型的擬合結果見表4。從模型的建立精度來看，10個模型的R2范圍為0.61～0.95，RMSE范圍為18.3～51.6 g。多項式模型和指數模型明顯好于冪函數模型； 以DL和D2L為變量的模型顯著好于以D或D2為變量的模型； 所有模型中以DL為變量的多項式模型和以D2L為變量的指數模型擬合效果最好，R2為0.93～0.95，RMSE為18.3～22.4 g。

從模型的檢驗精度來看，10個模型的R2為0.55～0.83，RMSE為17.3～48.0 g。同樣也是多項式模型和指數模型好于冪函數模型，但以D2L為變量的模型顯著好于以D、D2和DL為變量的模型。

綜合模型建立精度與模型檢驗精度的結果，認為以D2L為變量的指數模型(BR=65.17e0.002D2L)最佳。

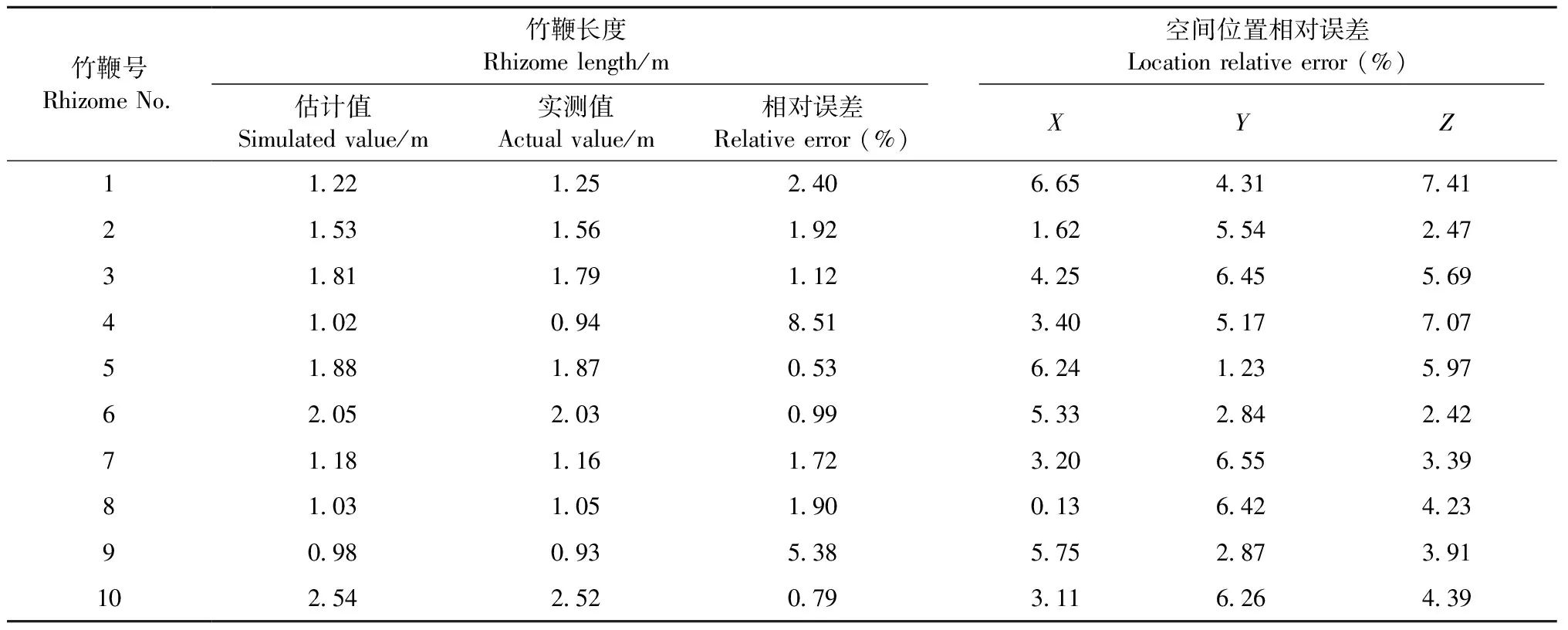
表3 竹鞭長度與空間位置探測精度檢驗結果Tab.3 Detection accuracy test results of bamboo rhizomes length and spatial position

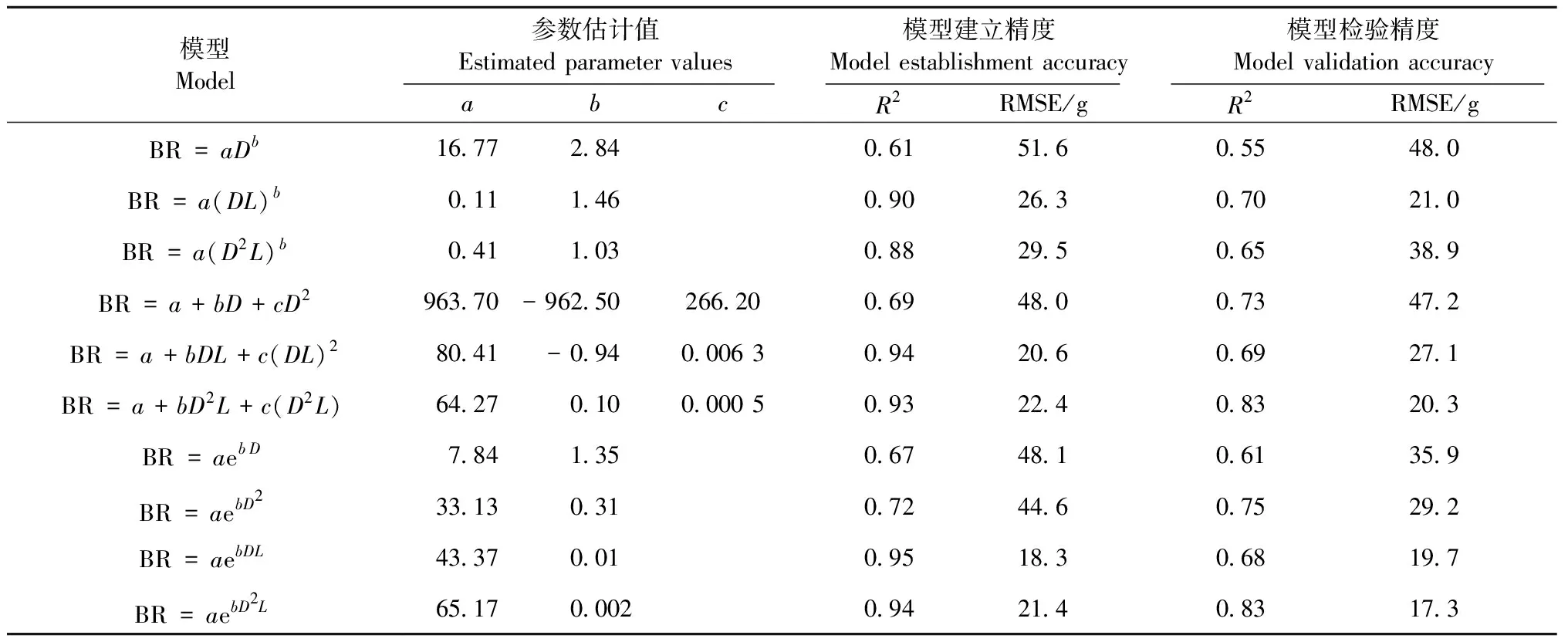
表4 竹鞭生物量模型參數擬合結果Tab.4 Fitting results of model parameters of bamboo rhizomes biomass

3.3.2 基于探地雷達數據的生物量模型精度檢驗 表5為基于10條竹鞭的實測與估計直徑及用最佳模型BR=65.17e0.002D2L計算的竹鞭生物量和實測生物量對比結果，表明用實測直徑計算的生物量與實測生物量相比，RMSE為7.87～33.23 g，用估計直徑計算生物量與實測生物量相比，RMSE為0.02～41.08 g，由此可見，基于估計直徑和實測直徑的生物量計算結果相差不大，二者沒有顯著差異。因此該生物量模型適用于探地雷達估計竹鞭直徑作為輸入數據，誤差不會顯著增加。

4 討論

自20世紀60年代起我國就對毛竹林竹鞭展開研究，主要涉及竹鞭的數量(廖光廬， 1988; 鄭郁善等， 1998)、空間分布(高培軍等， 2003； 胡超宗等， 1994)、生長動態(吳萌等， 1984; 周本智， 2006)和生物量(陳輝等， 1998； 李振基等， 1993)等方面。研究時間集中在20世紀80—90年代到2000年初，近幾年鮮有毛竹林竹鞭研究。這主要是由于試驗手段限制，以及研究熱點大多關注于地上生產力及其碳匯潛力而忽略了地下部分。過去竹鞭研究主要是通過挖掘法調查竹鞭，費時費力且有破壞性，而且無法重復觀測竹鞭動態發展過程，造成研究無法深入和遠落后于地上研究； 由于竹鞭與地上立竹是相連的整體，這也阻礙了對竹林生態系統整體高效固碳機理過程的探索。

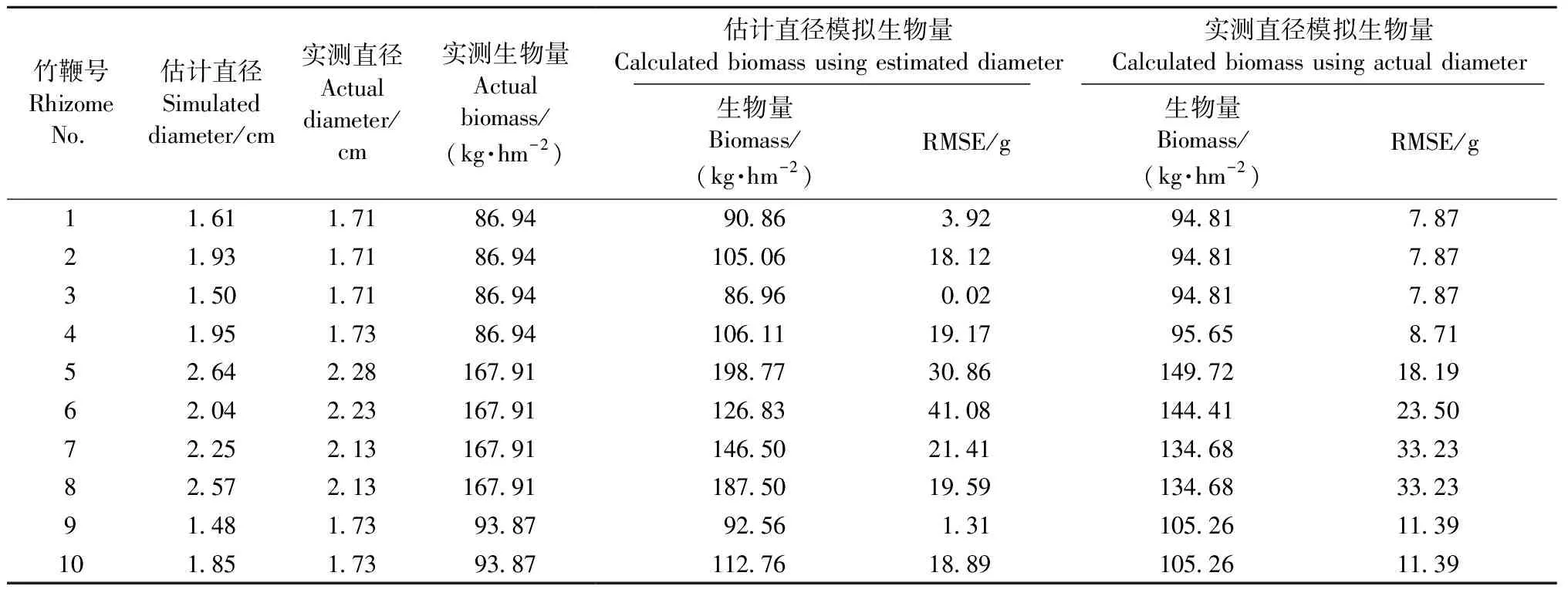
表5 竹鞭生物量模擬結果Tab.5 Simulated results of bamboo rhizomes biomass

GPR技術應用于探測植物根系的研究始于1999年(Hruskaetal., 1999)，經過20年發展，目前可用于樹木根系制圖、根徑大小及根系生物量的估算 (Butnoretal., 2012; Hiranoetal., 2009; 崔喜紅等， 2009)。但由于一般樹木根系分布土層深入地下幾米甚至十幾米，且以細根為主，給GPR探測帶來了困難，造成探測精度有限(Cuietal., 2011)。樹木根系的分布土層較深，生長方向朝下，剖面重疊度高，粗細不一等給GPR探測根系結構帶來了困難，但毛竹林的竹鞭均分布在淺層土壤(大部分在0～40 cm土層)、大多是水平方向生長、竹鞭直徑相對均一且較大(一般2～4 cm)，且毛竹林為單一樹種，地表灌草層相對較少，因此毛竹竹鞭是GPR探測的理想對象，比其他樹種根系探測要容易的多。因此，本研究發展一種基于GPR的毛竹林地下竹鞭空間結構無損探測方法，可有助于解除地下竹鞭觀測的困難。

本研究表明，毛竹林的地下竹鞭較易探測，雷達信號強烈，竹鞭位置信息方便提取，從而可分析竹鞭的垂直和水平分布特征。同時可利用雙曲線模型估計竹鞭直徑，并進一步估計竹鞭生物量，效果都較好。因此，利用GPR探測毛竹竹鞭空間結構及生物量是可行的。

基于本研究發展的毛竹林竹鞭GPR探測方法以及竹鞭直徑與生物量模型，下一步還需要在各種野外條件下開展大量研究和應用，來檢驗和完善該方法與模型。比如不同經營歷史、經營類型、經營強度毛竹林分的應用精度是否有差異，不同土壤類型、土壤質地、土壤水分條件對該應用是否有影響，等等。另外，毛竹林地下部分除了有較易利用探地雷達探測的竹鞭，還有大量較難精確探測的細根，下一步還需通過挖掘試驗分析竹鞭和細根的空間分布關系以及二者生物量的比例關系，然后通過竹鞭生物量及其空間分布來估計細根生物量及其空間分布，并在此基礎上，進一步探討不同經營歷史、經營類型、經營強度等對竹鞭空間結構及動態變化的影響，以及地下竹鞭與地上立竹的相互關系及其動態規律等。

5 結論

本研究發展了一種毛竹林地下竹鞭空間結構的GPR無損探測方法，可利用GPR探測地下竹鞭的位置信息，得到竹鞭垂直和水平方向的空間結構； 同時建立了估計竹鞭直徑、長度、生物量的模型，擬合效果較好。但還需通過大量不同野外條件的研究和應用來完善提出的方法和模型，提高其可靠性以及精度。