具無界中立系數的三階非線性微分方程解的振動性和漸近性

曾云輝，汪志紅*，汪安寧，羅李平，俞元洪

（1.衡陽師范學院數學與統計學院，湖南衡陽421008；2.中國科學院數學與系統科學研究院，北京100190）

0 引 言

考慮具無界中立系數的三階非線性微分方程

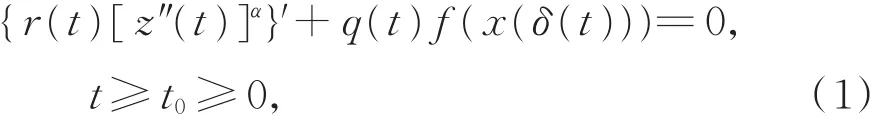
其中，z(t)=x(t)+p(t)x(τ(t))，f(x)∈C(R，R)，

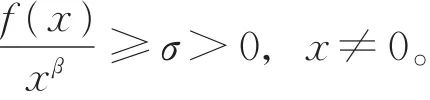
下文總假設下列條件成立：

(H1)α和β是 2個正奇數之比，

(H2)r(t) ∈C1(I，R+)，r"(t) ≥ 0，q(t) ∈C1(I，R+)，p(t)∈C(I，[1，∞ ))且p(t)不恒等于 1；

(H3) τ(t)，δ(t)∈C(I，(0，∞ ))，τ(t)≤t，δ(t)≤t，τ(t)在 I上 是 嚴 格 遞 增 的 函 數 ，且

考慮以下2種情況：

和

式（1）的解指函數 x(t)∈ C1[Tx，∞ )，Tx≥t0使得r(t)[z″(t)]α∈C1[Tx，∞ )且在 [Tx，∞ )上滿足 式（1） 。 本 文 僅 考 慮 式 （1） 中 滿 足sup{|x(t)|：t≥T}＞0對一切T≥Tx成立的解。如果式（1）在[Tx，∞)上有任意大于零的點，則稱其是振動的，否則，稱其是非振動的。

中立型方程解的振動性和漸近性問題具有重要的理論和實踐意義，例如，中立型微分方程可應用于核物理中原子核內部的電動勢及高速計算機無損傳輸電路的網絡設計等。對式（1）的振動性和漸近性研究越來越受關注［3-17］，以下為特例和更一般形式的方程：

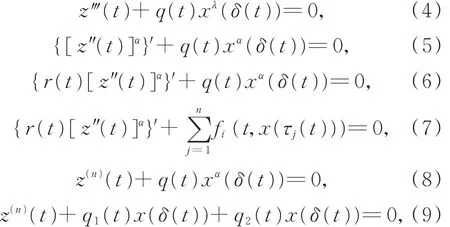
其中，λ，α＞ 0，n≥ 3，且n為正奇數。

近年來，文獻［3-9，12，14-17］用不同方法研究了三階中立型微分方程的振動性，得到了一些很好的結果，但其中大部分是式（1）的特例或與-1＜p0≤ p(t)≤ 0，0≤ p(t)≤ p0＜ 1 或 0≤ p(t)≤ p0＜∞的情況有關，而在p(t)＞1時關于三階中立型微分方程的振動結果尚不多見。例如，文獻［11-13］分別研究了式（8）、式（9）和式（6）的振動性，給出了一些振動結果，而這些結果是在條件τ?δ=δ?τ或τ?δ=δ?τ和 τ?σ=σ?τ下得到的，限制性較強，條件不易滿足。最近，文獻［14-15］取消了限制條件τ?δ=δ?τ，分別給出了式（4）和式（5）在正則條件下解的振動準則，但均未考慮非正則的情況，因此，研究式（1）在條件τ?δ≠δ?τ和非正則條件下的振動性問題是有意義的。

注 意 到 當 r(t)=1，α=β＞0，f(x(δ(t)))=xα(δ(t))時，式（1）變為式（5）。當 r(t)=1，α=1，β = λ，f(x(δ(t)))=xλ(δ(t))時，式（1）變為式（4）。因此，式（1）更具一般性，研究式（1）很有意義。

受文獻［14］的啟發，在條件τ?δ≠δ?τ和α≠β下，對式（1）展開研究，分別建立在正則條件

和非正則條件

下，式（1）的解x(t)或振動或漸近收斂于零的若干新的振動準則，所得結果推廣、改進和統一了最近文獻中若干熟知的結果。

如果沒有特別說明，均假設下文中出現的函數不等式最終成立，即對一切充分大的t成立。

1 主要結果

為書寫方便，引入記號：

其中，τ-1是 τ的反函數，m(t)和a(t)是本文設定的函數。

引理1 設(H1)～(H3)成立，x(t)是式（1）的正解，則當t≥t1，t1充分大時，z(t)具有下列3種性質：

(I)z(t)＞ 0，z"(t)＞ 0，z″(t)＞ 0，z?(t)≤ 0，{r(t)[z″(t)]α}"≤ 0；

(II)z(t)＞ 0，z"(t)＜ 0，z″(t)＞ 0，z?(t)≤ 0，{r(t)[z″(t)]α}"≤ 0；

(III)z(t)＞ 0，z"(t)＞ 0，z″(t)＜ 0，{r(t)[z″(t)]α}"≤ 0。

特別地，當式（10）成立時，z(t)滿足性質（I）和（II）。

證明 引理1的證明類似于文獻［17］中引理1的證明。此證略。

引理2 設(H1)～(H3)及p*(t)＞0成立，x(t)是方程（1）的正解，且z(t)滿足性質（II）。若

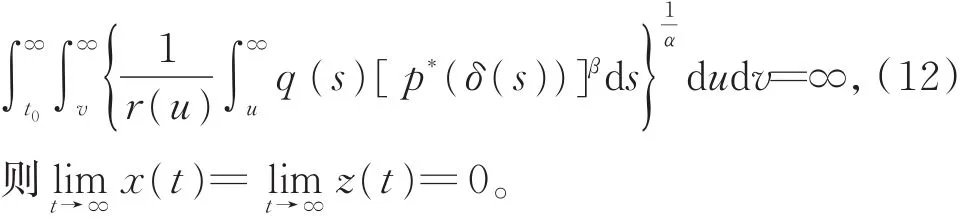
證明 設x(t)是方程（1）的最終正解，且z(t)滿足性質（II），即存在 t1∈[t0，∞)，當 t∈[t1，∞)時，有 x(t)＞ 0，x(τ(t))＞ 0，x(δ(t))＞0。 由 z(t)的定義，有

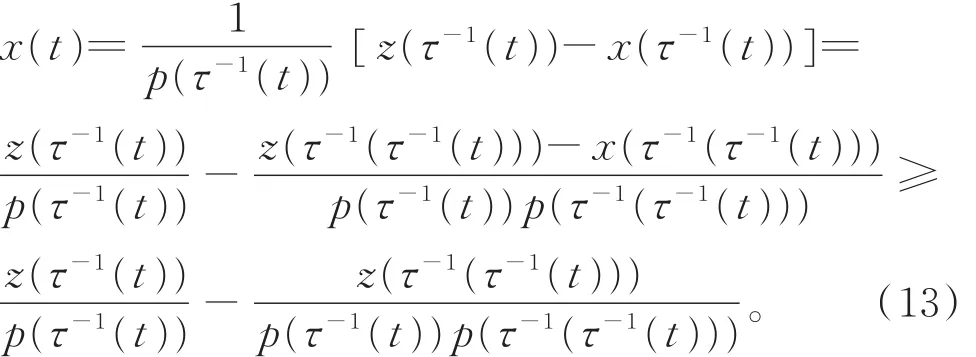
由于z(t)為減函數且τ(t)≤t，所以有

將式（14）代入式（13），有

從而有

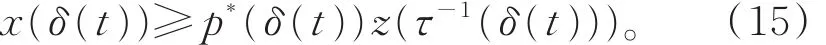
由式（1）和式（15），有

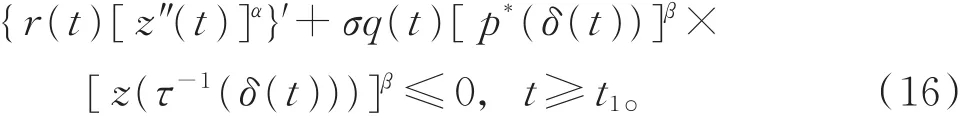
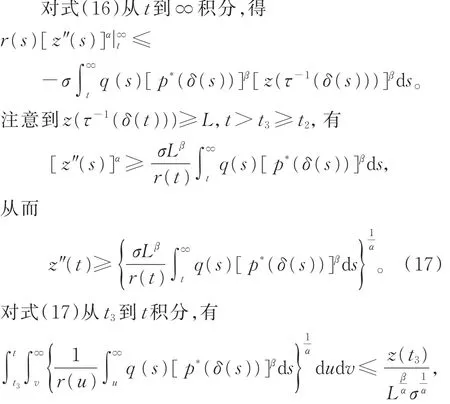
與 式（12）矛 盾 ，因 此 L=0。 又 由 于 0＜x(t)≤z(t)，因此

引理2得證。

引理3［2］設A＞ 0，B＞ 0，X ≥ 0，則

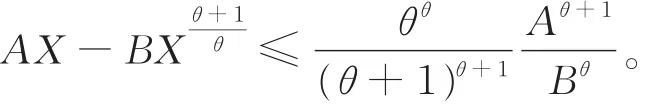
引理 4［1］設 f(t)∈ Cn([t0，∞ )，R+)，若 f(n)(t)對一切充分大的t最終定號，且存在t1≥t0，使得f(n-1)(t)f(n)(t)≤0對一切 t≥t1成立。如果則對任意 λ∈(0，1)，存在 tλ∈[t1，∞ )，使得在[tλ，∞ )上，有

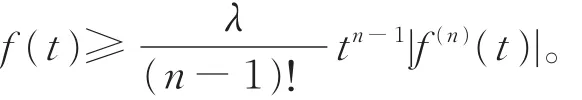
引 理 5［3］設 函 數 y(t)滿 足 y(i)(t)＞ 0，i=0，1，…，k，且 y(k+1)(t)≤ 0，則有

引理6 設(H1)～(H3)和p*(t)＞0成立，x(t)是方程（1）的最終正解，且z(t)滿足性質（I），若存在函數 m(t)∈ C1(I，R+)，滿足

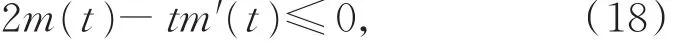
則z(t)滿足

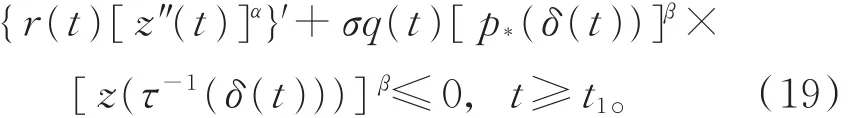
證明 設x(t)是方程（1）的最終正解，即存在充 分 大 的 t1，使 得 當 t≥ t1≥ t0時 ，有 x(t)＞ 0，x(τ(t))＞0，x(δ(t))＞0。 則式（18）和 τ-1(δ(t))＞t1成立（當x(t)最終為負時，可類似證明）。由引理2的證明，得到式（13）。又因為z(t)滿足性質（I），由引理5可得

故

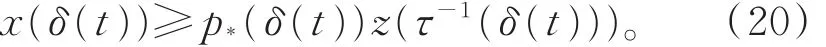
由式（1）和式（20），可得式（19）。

引理6得證。

引理6" 設(H1)～(H3)和Q(t)＞0成立，x(t)是式（1）的最終正解，且z(t)滿足性質（III），若存在函數 a(t)∈ C1(I，R+)，滿足

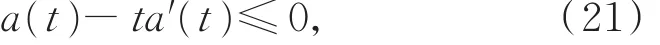
則z(t)滿足

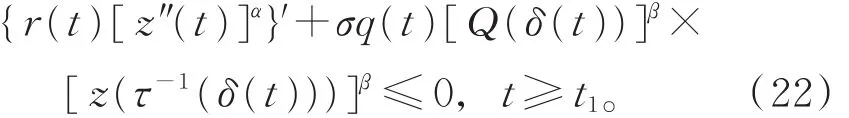
證明 與引理6的證明類似。此證略。

下面介紹本文的主要結果。

定理1 設(H1)～(H3)和式（12）成立。若式（10）和

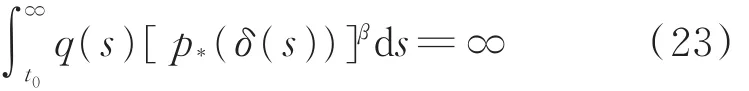
均成立，則式（1）的解x(t)都是振動的，或當t→∞時，x(t)→ 0。

證明 設式（1）存在非振動解x(t)。不失一般性，設 x(t)最終為正，由引理 1和式（10），z(t)只可能滿足性質（I）和（II）。若z(t)滿足性質（I），則由引理6，得式（19）成立，對式（19）從t1到t積分，有

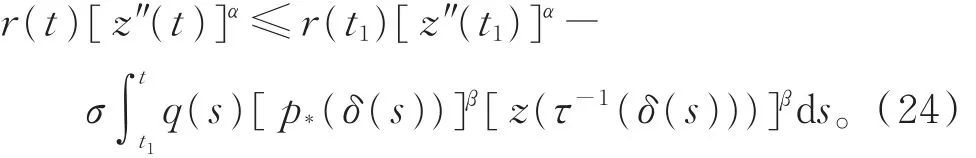
因 z(t)＞ 0，z"(t)＞ 0，故存在常數 M ＞ 0，使得當z(t)≥ M 時，有

進一步考慮，如果式（10）和式（23）其中之一不滿足，將如何彌補？為此，首先考慮式（23）不成立的情況。

定理 2 設(H1)～(H3)、式（2）和式（12）成立。若式（10）成立且存在函數 m(t)∈C1(I，R+)，則滿足式（18）。對于充分大的 t，有 p*(t)＞ 0和 p*(t)＞ 0。如果存在函數 η(t)∈C1(I，R+)、常數 λ∈(0，1)和L0＞ 0，滿足

則式（1）的解x(t)都是振動的，或者當t→∞時，x(t)→ 0。

證明 設式（1）存在非振動解x(t)。不失一般性，設 x(t)最終為正，即存在t1∈[t0，∞ )，當 t≥ t1時，使得 x(t)＞ 0，x(τ(t))＞ 0，x(δ(t))＞ 0， p*(t)＞ 0，p*(t)＞0，τ-1(δ(t))＞t0及式（18）成立（當 x(t)最終為負時，可類似證明）。因式（10）成立，故z(t)只可能滿足性質(I)和(II)。首先，設z(t)滿足性質(I)，由引理 5，可得

m(t)∈C1(I，R+)滿足式（18）。對于充分大的 t，滿足 p*(t)＞0 和 p*(t)＞0，如 果 存 在 函 數η(t)∈C1(I，R+)、常 數 λ∈(0，1)、L0＞ 0 和 m0＞ 0，滿足

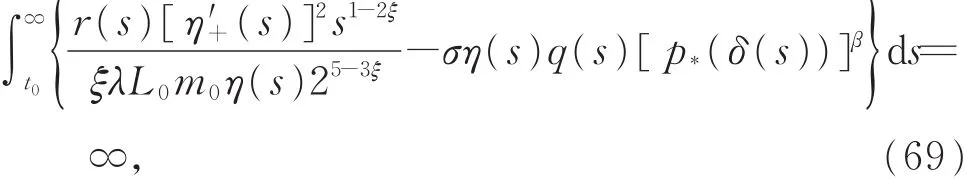
則式（1）的解x(t)都是振動的，或當t→∞時，x(t)→ 0。

證明 設x(t)是方程（1）的非振動解。不失一般性，設 x(t)最終為正，故存在 t1∈[t0，∞ )，當 t＞ t1時，使得 x(t)＞0，x(τ(t))＞0，x(δ(t))＞ 0，p*(t)＞0，p*(t)＞ 0，τ-1(δ(t))＞ t0及 式（18）成 立 。 因 式（10）成立，故 z(t)只可能滿足性質 (I)和(II)。首先，設 z(t)滿足性質(I)，注意到式（3）和(H3)，類似于定理6的證明，可得式（67）。

同定理2，定義函數w(t)，由式（19）、式（27）～式（29）和式（67），可得

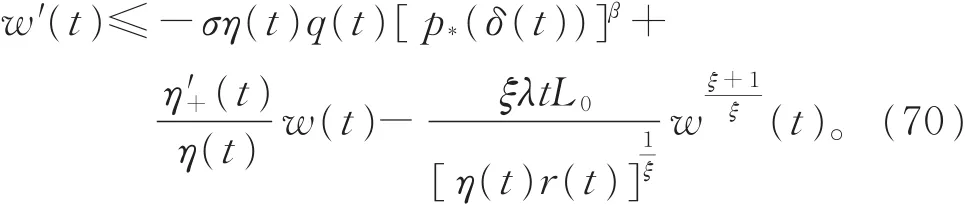
后續證明與定理3的證明類似，此證略。

3 例 子

例1 考慮具有無界中立系數的三階非線性微分方程

故式（25）成立。因此，由定理2知，式（71）的解x(t)都是振動的或者漸近收斂于零。由于α≠β，因此文獻［3-16］及其引文中的振動結果均不適用于式（71）。