巴拿赫空間中演化過程非一致指數二分性的Datko-Pazy型定理

岳田 ，宋曉秋

（1.湖北汽車工業學院理學院，湖北十堰442002；2.汽車動力傳動與電子控制湖北省重點實驗室(湖北汽車工業學院)，湖北十堰442002；3.中國礦業大學數學學院，江蘇徐州221116）

近年來，關于微分系統定性理論的研究取得了突破性進展，尤其是在指數漸近性方面，大量公開問題的解決，推進了相關理論的拓展和完善［1-13］。1930 年，PERRON［1］在有限維空間中利用輸入-輸出方法（又稱Perron方法或測試函數方法）建立了齊次微分方程x˙(t)=A(t)x(t)解的指數漸近性（指數二分性）與對應的非齊次微分方程x˙(t)=A(t)x(t)+f(t)之間的關系。隨后，MASSERA等［2］在此基礎上，將結果擴展到無限維空間，并首次研究相應微分系統的非一致指數漸近性。2010年，BARREIRA 等［3］通 過 定 義 合 適 的 范 數（又 稱Lyapunov范數），討論了演化過程非一致指數穩定性與容許性之間的關系。此后，基于Lyapunov范數獲取非一致指數漸近性（指數穩定性、指數膨脹性、指數二分性、指數三分性）成為一種重要的技術手段，文獻［4］基于具有非一致指數增長的演化族（演化過程），研究了非一致指數二分性與函數空間對(Lp(X)，Lq(X))的容許性之間的關系，獲得了刻畫非一致指數二分性的Perron型結論；文獻［5］給出了非一致指數增長的半流上的強連續上閉鏈的非一致指數二分性存在的容許條件。值得一提的是，文獻［6］基于 Lyapunov 范數將 DATKO［7-8］和 PAZY［9］的相關經典結論擴展到非一致指數增長的演化過程，得到了非一致指數穩定性與非一致指數二分性的Datko-Pazy型定理的連續形式。

定理1［6］設Φ為非一致指數增長的演化過程，且滿足 Φ(t，t0)P(t0)=P(t)Φ (t，t0)，t≥ t0≥ 0，則 Φ呈非一致指數二分性，當且僅當存在常數p，K，m＞0，使得

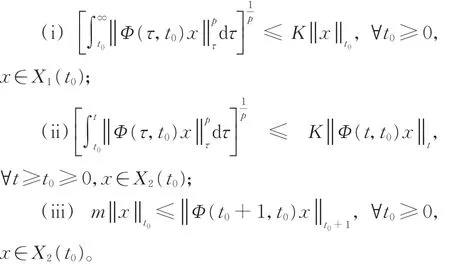
由定理1知，非一致指數二分性意味著Φ在子空間X1(t0)上呈非一致指數穩定性，在補子空間X2(t0)上呈非一致指數膨脹性，即條件（i）刻畫了Φ的非一致指數穩定性；而對Φ的非一致指數膨脹性的刻畫需要同時滿足條件（ii）和（iii）。

受文獻［6］的啟發，基于Lyapunov范數建立了Banach空間中刻畫演化過程非一致指數二分性的其他連續與離散形式的Datko-Pazy型定理，所得結果推廣并完善了指數穩定性與指數二分性理論中部分 已 有 結 果（如 DATKO［7-8］、PAZY［9］、PREDA等［4，6］等）。需要說明的是，本文簡化了定理 1中關于刻畫非一致指數膨脹性的條件，結論更為簡潔。

1 預備知識

設X是Banach空間，Θ是度量空間，將空間X上的范數及作用其上的有界線性算子的全體B(X)的范數記作||·||。記I為恒等算子，[a]表示不超過實數a的最大整數，M(R+，X)表示所有從R+到X的Lebesgue可測函數構成的集合。

定義1［6］如果滿足：

（i）Φ (t，t)=I， ?t≥ 0；

（ii）Φ(t，s)Φ(s，t0)= Φ (t，t0)，?t≥ s≥ t0≥ 0；

（iii）Δ × X ?(t，s，x)? Φ(t，s)x ∈ X連續；

（iv）?ω∈R 及 M：R+? (0，∞)使 得 對 ?t≥t0≥ 0，x∈ X，有

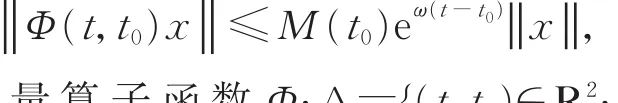
則 稱雙變 量 算 子 函 數 Φ：Δ={(t，t0)∈R：t≥ t0≥0}→ B(X)，(t，t0)? Φ(t，t0)為非一致指數增長的演化過程。

注 1［6］則稱 Φ為一致指數增長的演化過程。

記

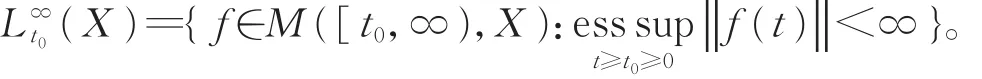
為與文獻［6］保持一致，令

假定X1(t0)是閉的且容許一個閉補子空間X2(t0)，P(t0)為 X1(t0)上的投影算子，即 Im P(t0)=X1(t0)，同時令Q(t0)=I-P(t0)。

注 2［6］對 ?t≥ t0≥ 0，有

（i）P(t)Φ (t，t0)P(t0)= Φ (t，t0)P(t0)；

（ii）若 x∈ X2(t0)，x ≠ 0，則 Φ(t，t0)x≠ 0。

設Φ為非一致指數增長的演化過程，記

定義2［6］設Φ為非一致指數增長的演化過程，若 存 在 常 數 N1，N2，v＞ 0，使 得 對 ?t≥ t0≥ 0，x∈X，有

則Φ呈非一致指數二分性。

注 4［6］在定義 2中，若Q(t0)=0，則 Φ呈非一致指數穩定性；若P(t0)=0，則Φ呈非一致指數膨脹性。

引理 1［10］設 f，g：R+→ R+，其中 g為連續函數且 g(t)＞ 0(?t＞ 0)。若滿足：

（i）f(t)≥ g(t-t0)f(t0)，?t≥ t0≥ 0；

（ii）存在λ＞ 0滿足g(λ)＞ 1，

則存在常數 N，v＞ 0，使得對 ?t≥ t0≥ 0，有 f(t)≥Nev(t-t0)f(t0)。

2 主要結論

定理2 設Φ為非一致指數增長的演化過程，且滿足 Φ(t，t0)P(t0)=P(t)Φ (t，t0)，t≥ t0≥ 0，則 Φ呈非一致指數二分性當且僅當存在常數p，K＞0，使得

證明 必要性。由定義2立即可得。

充分性。由定理1的證明（詳見文獻［6］第578頁）可知，條件（i）意味著定義 2（i）成立，因此，僅需借助條件（ii）來證明定義 2（ii）。

設t≥t0≥0，x∈X，且Q(t0)x≠0，

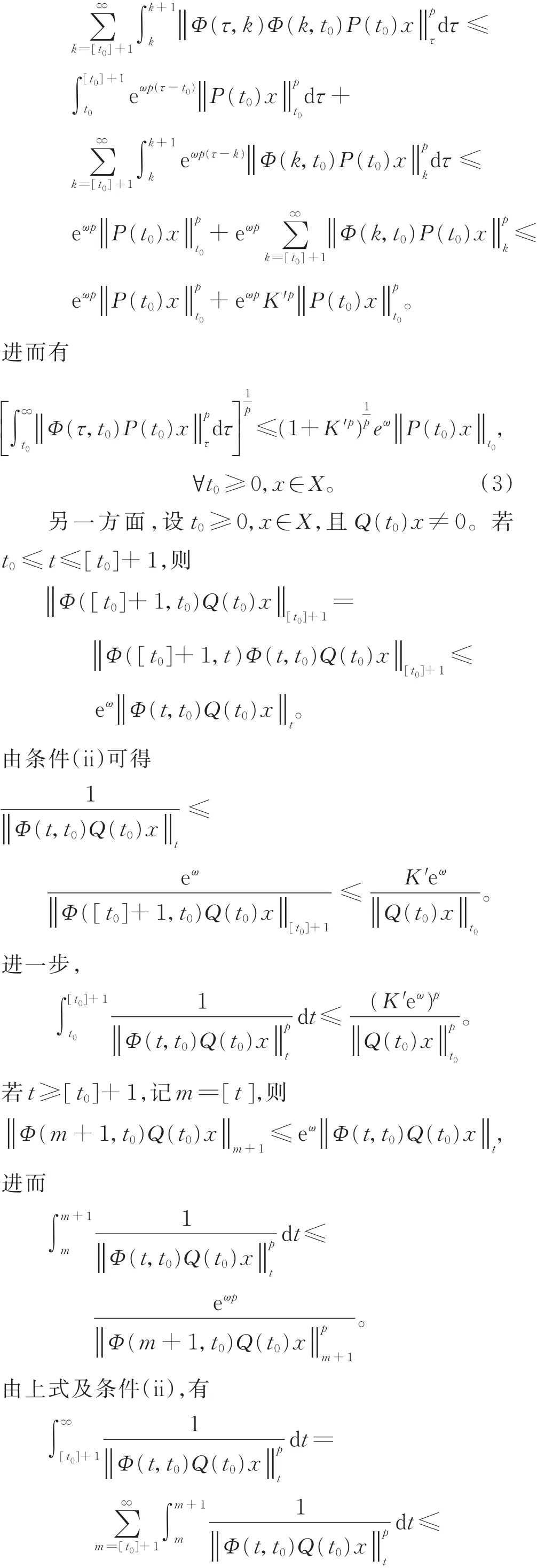
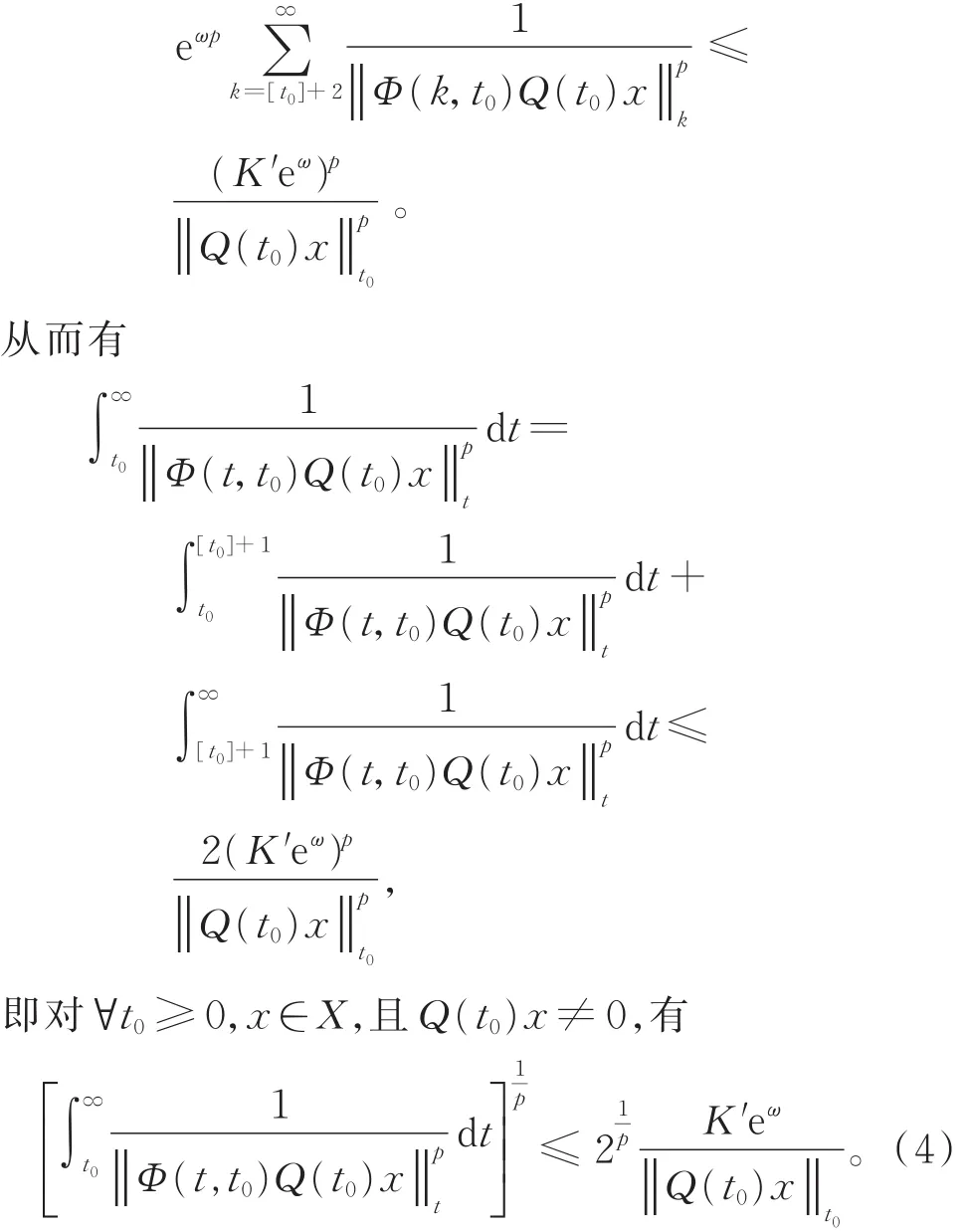
由式（3）和式（4），結合定理2可得結論成立。

定理3得證。

注5［6］設Φ為非一致指數增長的演化過程，定理2與定理3分別給出了刻畫其非一致指數二分性存在的連續與離散形式。在這2個定理中，若Q(t)=0，則可得到Φ滿足非一致指數穩定性的充要條件，即文獻［6］中的定理 3.1；若P(t)=0，則可得到Φ滿足非一致指數膨脹性的充要條件。故得到的刻畫其非一致指數膨脹性條件較文獻［6］更簡潔。

文獻［6-7］分別給出了演化過程Φ的非一致指數穩定性和C0半群的一致指數穩定性與Lyapunov算子方程之間的關系，本文利用Lyapunov算子方程刻畫了Φ的非一致指數膨脹性。

推論1 若Φ為非一致指數增長的演化過程，則Φ呈非一致指數膨脹性，當且僅當存在W：R+×X → R+以及常數p，K"＞ 0，使得

若演化過程Φ呈非一致指數膨脹性，則由定義2可得條件（i）成立。

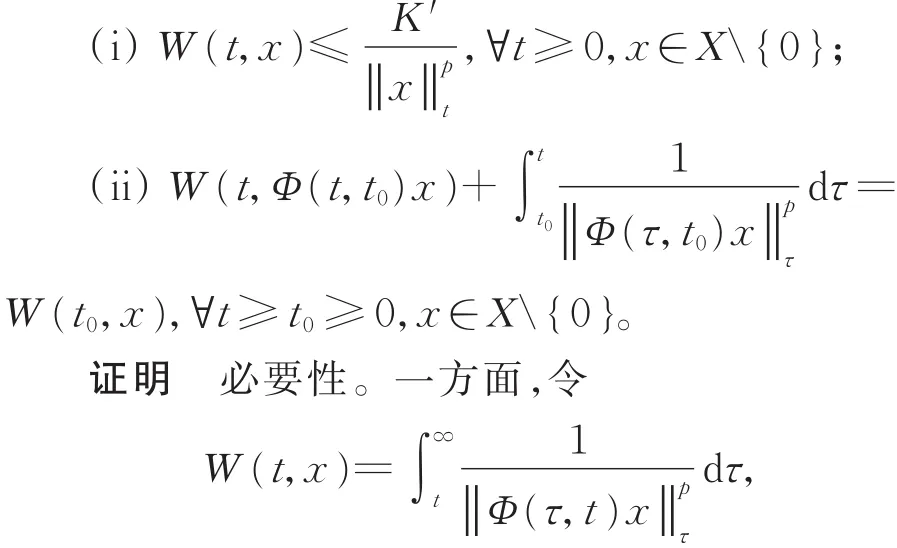
另一方面，

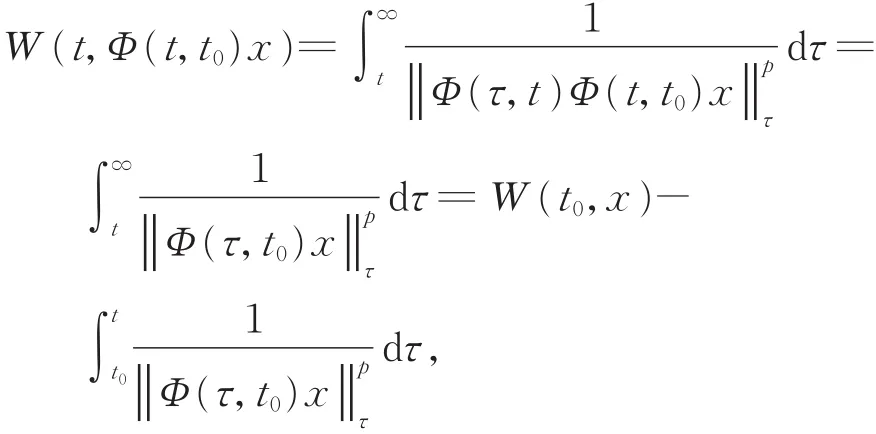
故條件（ii）亦成立。

充分性。由已知條件知，對 ?t≥t0≥0，x∈ X{0}，有

從而有

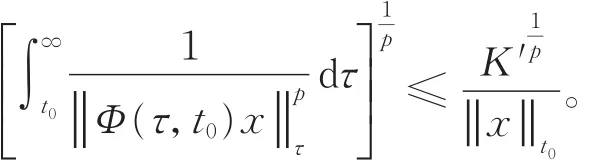
由定理2可得，Φ呈非一致指數膨脹性。

最后，給出定理1的離散形式。

定理4 若Φ為非一致指數增長的演化過程，且滿足 Φ(t，t0)P(t0)=P(t)Φ (t，t0)，t≥ t0≥ 0，則 Φ呈非一致指數二分性當且僅當存在常數p，K"＞0，使得

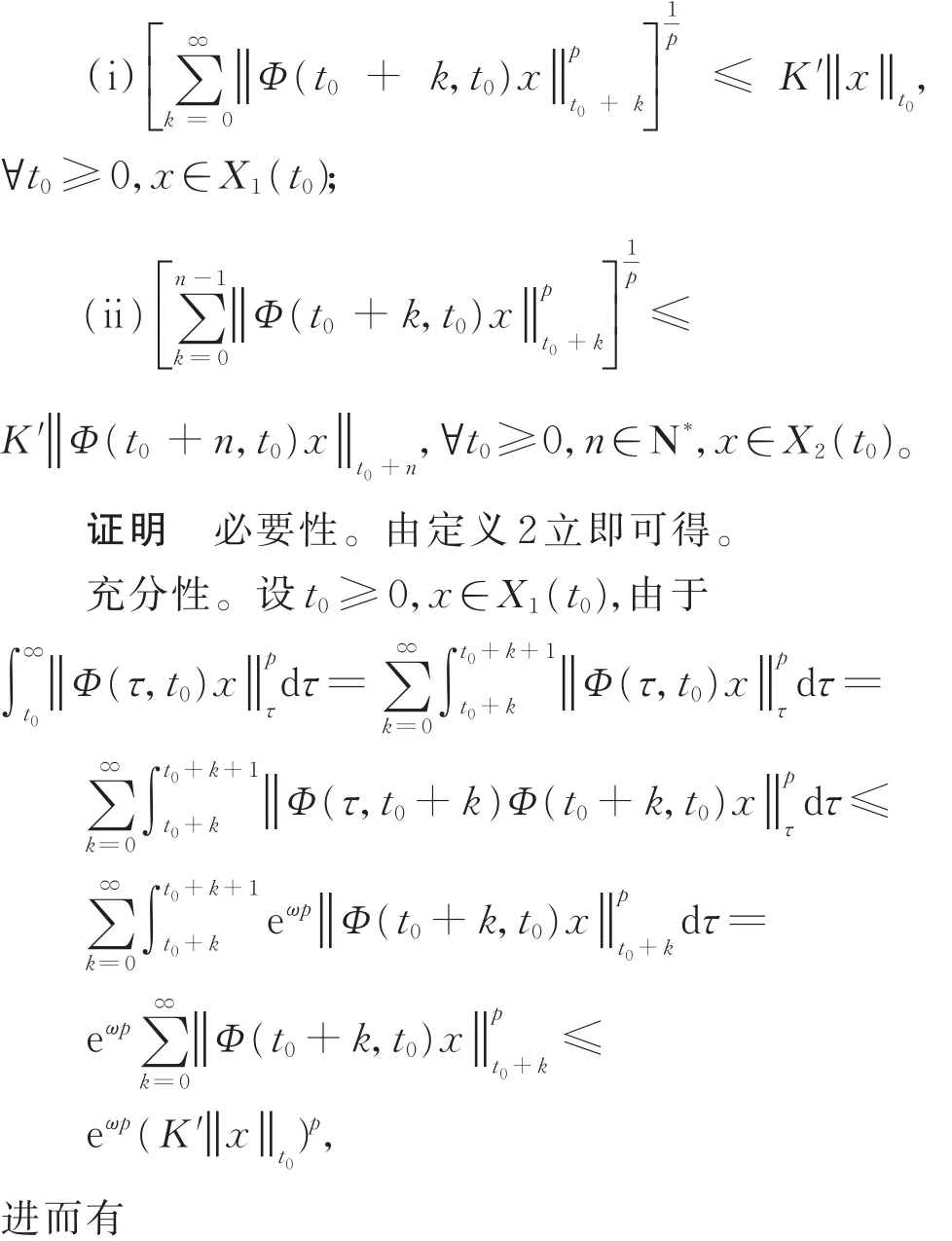
由式（5）～式（7），取 K=K"e2ω，m=1 K"，可得定理 1中的條件（i）～（iii）成立，故 Φ呈非一致指數二分性。