基于最小二乘參數辨識的電纜早期電弧故障測距

張璇，周正雄，朱鵬

(1. 國網湖南省電力有限公司張家界供電分公司，湖南張家界427000；2. 長沙理工大學電氣與信息工程學院，湖南長沙410114)

0 引言

地下電纜因為其短距離傳輸的經濟性[1]和惡劣環境下的輸電可靠性在城市電網中得到了廣泛應用[2-4]。但是在長期運行后, 電纜主體和附件的絕緣電阻會逐漸緩慢降低[5-6], 絕緣的逐步惡化導致電纜從 “安全” 運行狀態進入到 “帶病” 運行狀態[7]。在此期間電纜接頭及其附件容易發生局部放電現象, 頻繁的局部放電后期逐漸演變成為間歇性的電弧接地故障。從故障波形上看, 此類故障往往發生在電壓峰值處, 持續四分之一周期至四個周期內不等。它可能在一段時間內多次發生, 也可能很長一段時間不發生, 直至絕緣擊穿, 形成永久性故障[8]。

目前對于這種介于絕緣劣化和永久性擊穿之間的間歇性電弧故障研究較少, 國內外提出的測距方法按照理論基礎可分為兩大類: 阻抗法[10-12]和行波法[9]。文獻 [12] 利用故障過渡電阻為純電阻性質, 以故障電壓、電流及線路分布參數模型計算沿線各點的電壓與電流實現故障點定位, 但忽略了感抗。文獻 [13] 考慮了電纜金屬護層結構建立雙層阻抗電纜電路模型, 以參數辨識迭代法實現故障點測距, 但增加了模型復雜度, 未充分考慮線路耦合。文獻 [14] 針對架空線、電纜多段混合線路, 提出一種利用分段補償原理的改進雙端行波測距新方法。文獻 [15] 將零序電壓、電流暫態分量的衰減時間常數和頻率結合拉氏變換和雙曲函數線路模型, 提出一種基于特征根的電纜單端測距方法, 但該算法收斂性差, 測距精度易受外界影響。

針對上述測距方案的不足, 本文通過電纜不同早期故障形式下的狀態網絡, 結合故障數據采樣值, 建立了零模等效電路時域測距方程。對微分方程中的高階求導問題, 采用正弦逼近擬合零模信號, 從而克服差分近似代替造成的誤差大的缺陷。將過渡電阻、故障距離作為模型的未知參數, 代入到測距方程中進行最小二乘參數辨識, 選取合適的數據窗口計算過渡電阻。通過不斷移動數據窗口,得到過渡電阻的暫態估計值, 從而解得電纜早期故障距離。

1 電纜早期電弧故障特性

1.1 單芯交聯聚乙烯電纜結構

XLPE (交聯聚乙烯) 交流電纜主要有兩種結構, 即應用于35 kV 及以上電壓等級的單芯電纜和35 kV 以下電壓等級的三芯電纜。本文中選用的電纜模型如圖1、圖2 所示, 其中圖1 為單芯XLPE高壓電纜實物圖, 圖2 為單芯XLPE 高壓電纜剖面示意圖。

圖1 單芯XLPE 交流電纜實物圖

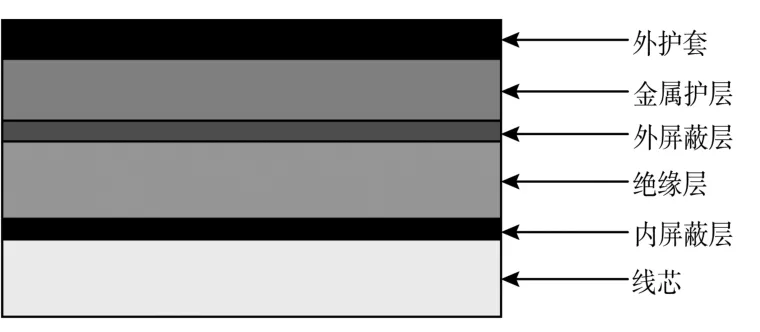
圖2 單芯XLPE 交流電纜剖面示意圖

單芯XLPE 交流電纜由線芯、內屏蔽層、絕緣層、外屏蔽層、金屬護層和外護套組成[16], 其主要結構參數見表1。

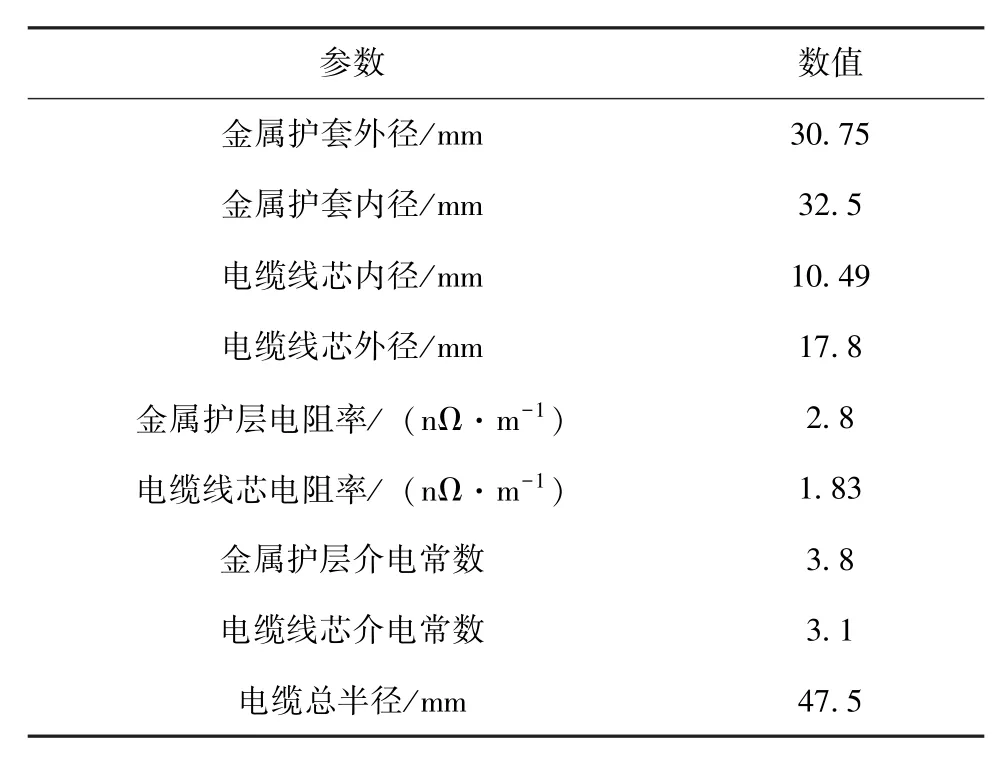
表1 電纜主要結構參數

1.2 電纜早期故障等效電路

電纜運行期間, 電纜護層某處絕緣缺陷點會發生頻繁的局部放電, 加快了絕緣老化。當缺陷點處含有水汽或者其他介質時, 會與地面產生高壓電弧現象并且散發的能量瞬間蒸發水汽使得電弧消失。當發生早期故障時, 電纜故障段的等效電路如圖3所示。

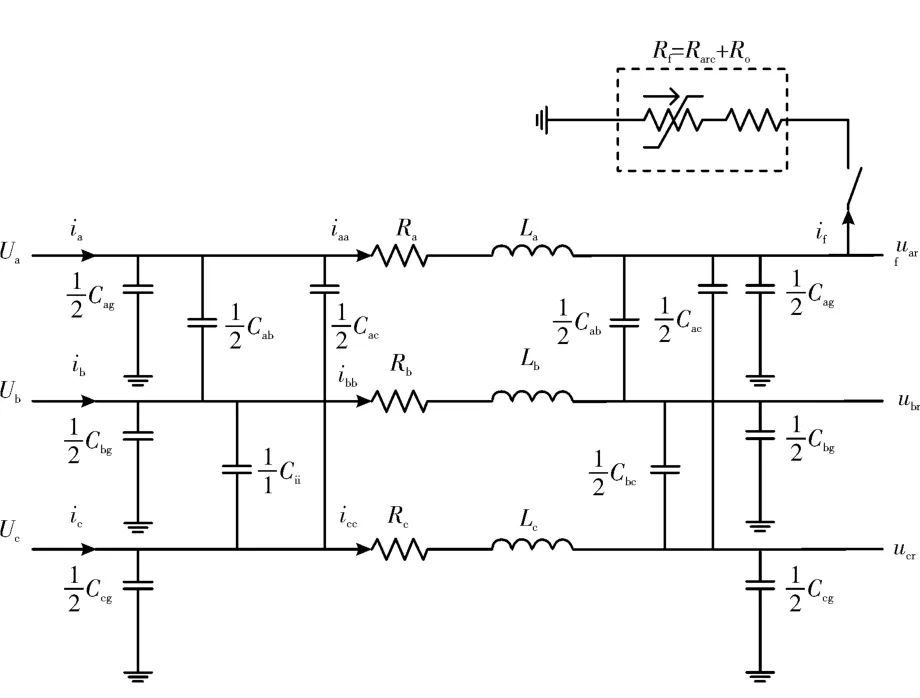
圖3 電纜單相早期故障等效電路

分析知A 相輸入電壓為:

式中,Ua為輸入端 A 相電壓；iaa、ibb和icc分別為各相電流；Ra和La分別為A 相單位長度電阻與電感；Lab和Lac分別為A 相與其他相之間單位互感；Rf和if分別為早期故障電阻和故障電流, 其中Rf近似于時變電弧電阻與固定電阻的疊加；x為故障點距離。

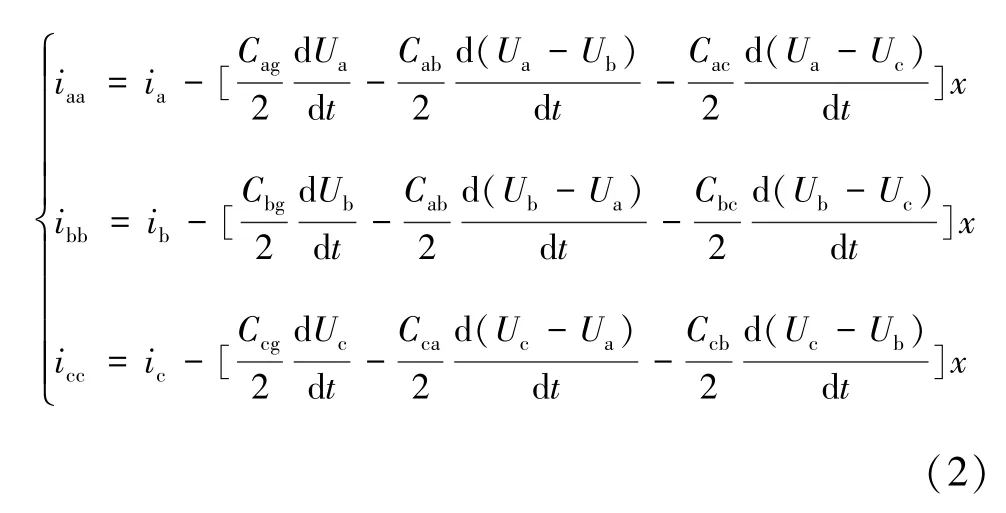
式中,Cag、Cbg和Ccg為單位長度對地電容；Cab、Cac和Cbc為單位長度相間電容。

故障電流if等于剩余電流:

1.3 電纜早期故障電弧模型

本文采用動態Cassie-Mayr 組合電弧模型模擬時變電弧電阻, 此模塊在PSCAD 上仿真的電弧電壓和電弧電阻結果如圖4 所示。可以看出電弧電阻在電流零休期間較大, 燃弧期間阻值近似為零, 能夠滿足時變特性。

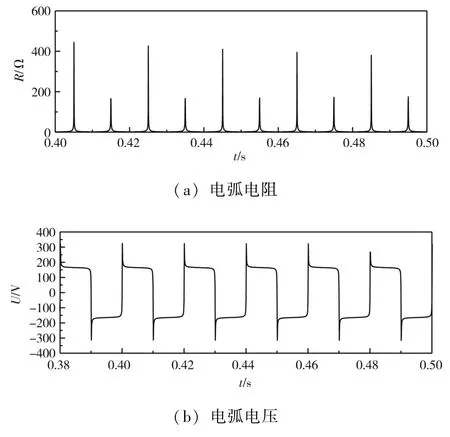
圖4 Cassie-Mayr 電弧模型特性

電纜早期故障根據暫態持續時長分為半周波和多周波早期故障, PSCAD 中電纜早期故障仿真結果如圖5 所示。可以看出在相同的條件下電纜半周波早期故障一般持續1/2 個周期, 而電纜多周波早期故障可持續1～3 個周期。

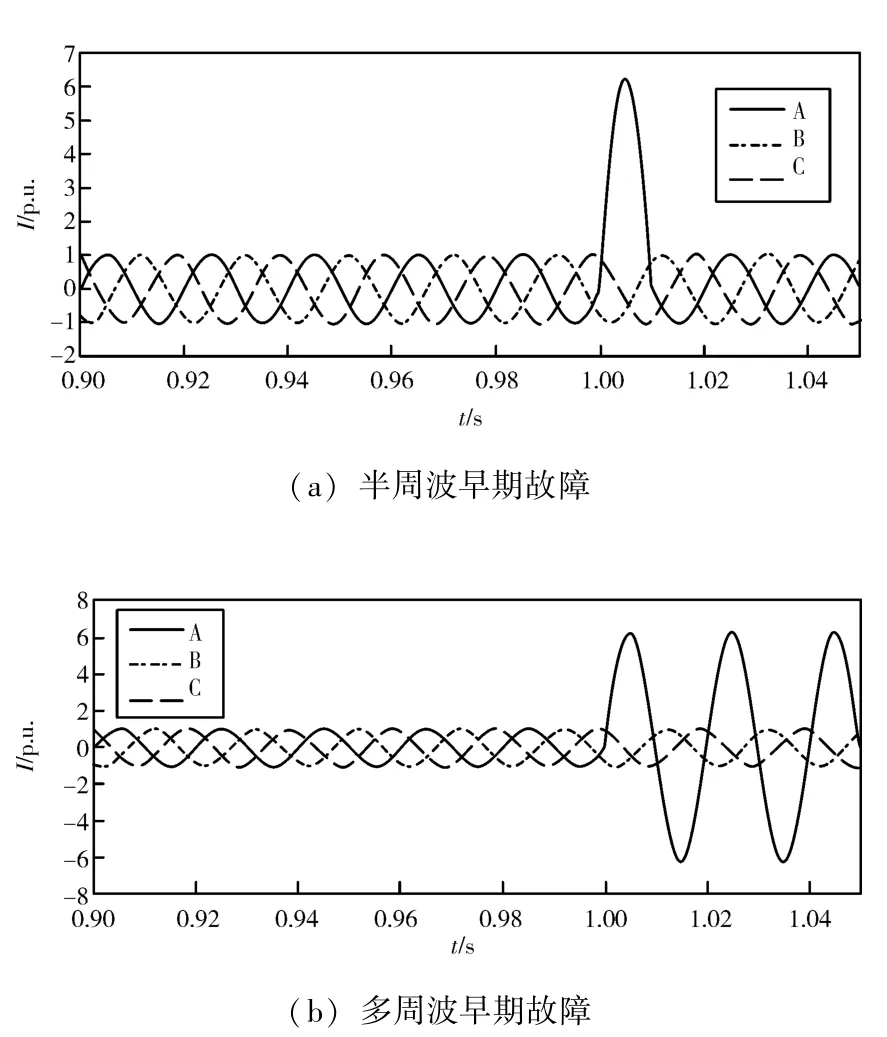
圖5 電纜半周波和多周波故障仿真結果

2 測距原理

2.1 故障狀態零模等效電路

故障A 相電壓的時域微分方程為:

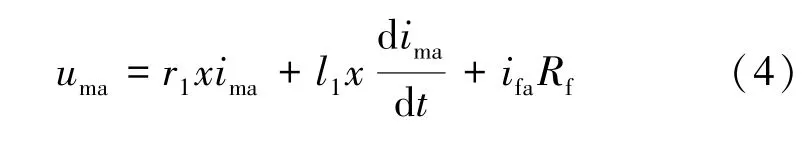
式中,r1、l1分別為線路單位長度一模電阻、一模電感,Rf為故障點至大地的過渡電阻。上式對流過線路電阻和電感的電流乘以零序補償系數后, 得故障電壓和故障電流:

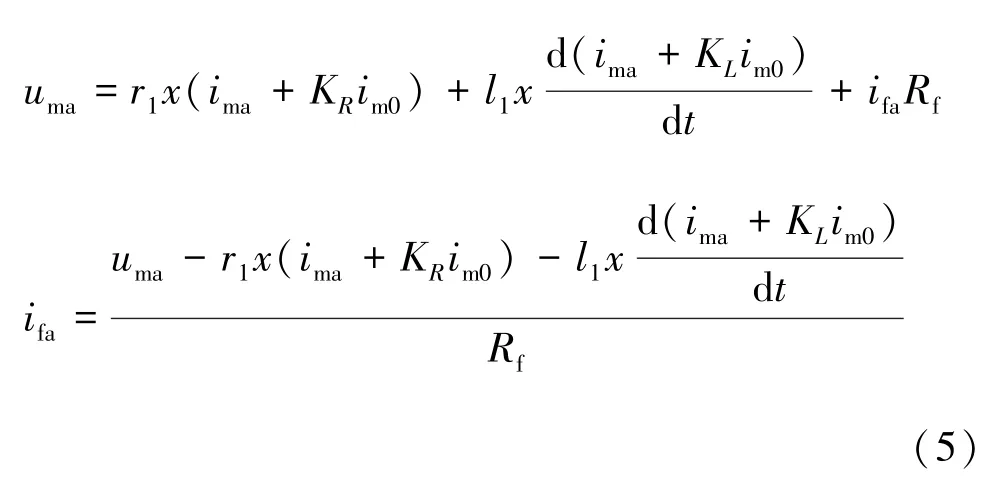
式中,KR、KL分別為電阻及電感分量的零序補償系數,im0為零模電流, 計算式見式 (6):

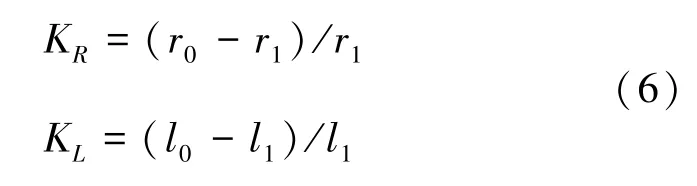
式中,r0、l0分別為線路單位長度零模電阻和零模電感。配電網故障狀態下的零模等效電路如圖6所示。

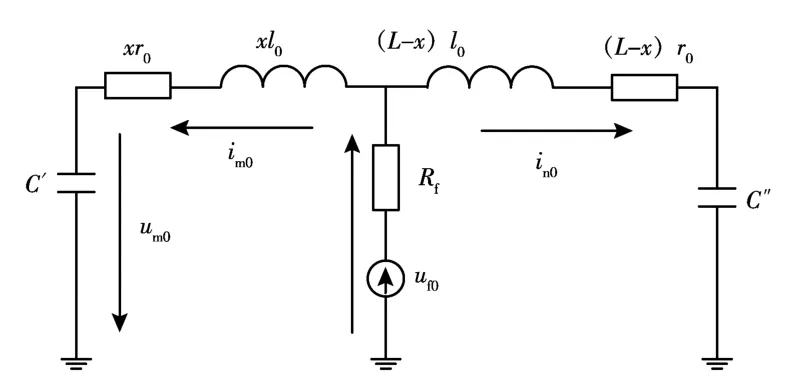
圖6 配電網故障零模等效電路

由故障點兩端的零模電壓相等可得到故障距離的微分方程為:

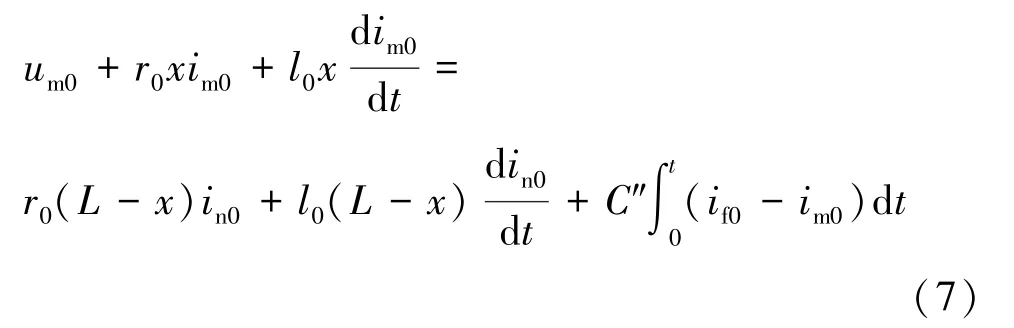
對上式求導得:

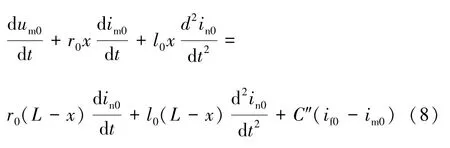
其中, 由相模變換可得故障點零模電流為:

可得測距方程矩陣:

其中, [A0,1,2,3,4,5,6] 為系數矩陣, 可由監測的電纜暫態三相電壓、電流求得。

2.2 正弦逼近法計算高階導

對于系數矩陣中的零模電壓、零模電流的高階求導, 為了減少差分等效帶來的誤差, 選擇利用正弦函數逼近擬合原零模采樣波形得到擬合的多項正弦函數表達式, 再求導得到精確的二階導、三階導系數。

以m 端的零模電流信號為例, 根據級數原理,零模電流信號的函數表達式可以用不同幅值和不同相位的各次正弦波疊加表示:

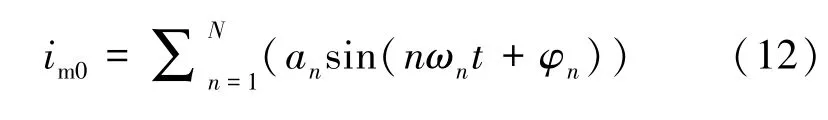
式中,an為幅值,ωn為角速度,φn為初相位。

通過不斷的修正每項正弦函數的幅值與相位,使擬合函數f(t) 與實際值誤差最小。

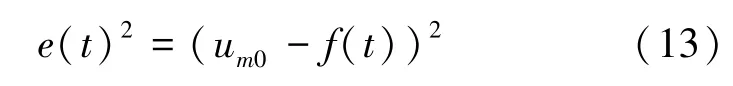
最后, 通過f(t) 的表達式計算從而得到系數矩陣[]。

2.3 芯―護層故障 (c-s)

當電纜導芯與金屬護層之間的絕緣因老化而破壞時, 兩者之間的過渡電阻會增加一個金屬護層的過渡電阻分量, 此時早期故障零模等效電路如圖7 所示。

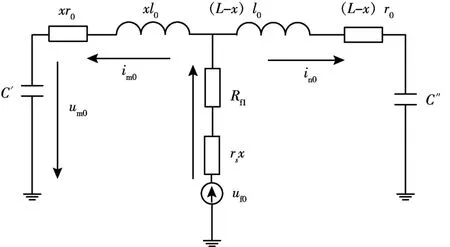
圖7 c-s 早期故障零模等效電路

式中,rs為電纜金屬護層單位長度電阻值。

此時電纜早期故障測距方程式 (10) 變為:

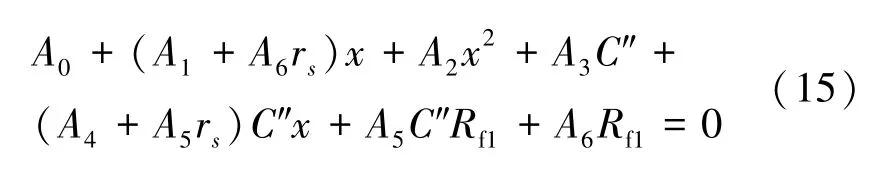
2.4 芯—護層接地故障 (c-s-g)

當電纜在芯—護層故障的基礎上, 發生局部外護套破損時, 電纜的鎧裝層直接接地或間接接地(經小阻抗) 時的早期故障零模等效電路如圖8所示。

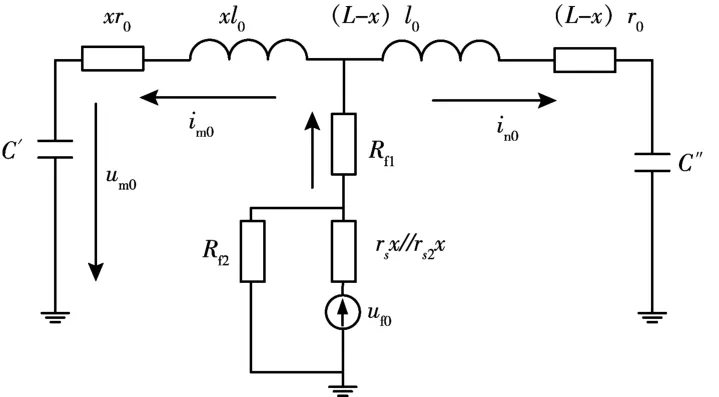
圖8 c-s-g 早期故障零模等效電路

此時的過渡等效電阻為:

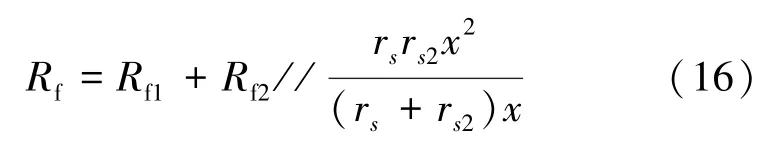
式中,rs2為外鎧裝層單位長度電阻。

此時電纜早期故障測距方程式 (10) 變為:

3 測距流程

正常運行狀態下, 電纜纜芯與銅屏蔽層之間的主絕緣和鋼帶鎧裝層與大地之間的外護套絕緣狀態良好, 理論上故障電阻Rf1和Rf2為無窮大。當電纜發生芯―護層故障后, 電纜主絕緣被破壞,Rf1降為某一定值,Rf2/Rf1比值較大。當電纜發生芯―護層接地故障后, 電纜兩處絕緣均被破壞,Rf1和Rf2同時降低, 且兩者均與電弧長度有關, 因此Rf2/Rf1比值較小。可利用這一特征區分電纜早期 (cs) 自恢復故障與 (c-s-g) 自恢復故障。

對于公式 (15) 和公式 (17), 系數矩陣[A0,A1,A2,A3,A4,A5,A6] 由式 (11) 求得,其中高階導部分用正弦逼近法消除差分誤差。當線路兩端的監測裝置或者其他錄波裝置發現監測波形中出現電壓峰值下降, 并持續時間在四分之一周波到兩個周波左右, 期間電壓接近恒定值等特征時,即可啟動自恢復故障檢測流程, 整體步驟如下:

步驟一: 選取合適的數據窗口, 記錄故障后的母線電壓、線路電流, 即uma(k)、umb(k)、umc(k)、ima(k)、imb(k)、imc(k) , 利用相模變換得到零模電壓、零模電流計算值序列um0(k)、im0(k)。

步驟二: 設置初始值, 包括故障距離初始值、過渡電阻初始值和對地電容初始值等。

步驟三: 將初始值代入到芯―護層故障測距方程式 (15) 進行最小二乘參數辨識, 得到故障電阻Rf1和Rf2, 根據兩者比值Rf2/Rf1辨別早期自恢復故障類型。

步驟四: 再將步驟二中初始值代入到已識別出的故障類型相對應的故障測距方程中, 進行最小二乘參數識別, 求解方程組未知常數之一的過渡電阻。

步驟五: 不斷地移動數據窗口, 重復步驟四,計算線路過渡電阻。如果隨著數據窗口的移動所得到的過渡電阻估計值穩定在一個數值范圍, 給出此時對應的故障距離估計值 。基于最小二乘參數辨識的電纜早期電弧故障測距整體流程如圖9 所示。

圖9 測距流程圖

4 仿真驗證

在PSCAD/EMTDC 中建立10 kV 系統三相單芯電纜供電模型, 模型參考文獻 [7]。其中電纜主要結構參數見表1, 電纜長度L設為10 km, 設定距離首端6 km 處發生半周波自恢復故障 (c-sg)。以10 kHz 的采樣頻率監測三相電壓、三相電流值, 并以10 個采樣點為一個數據窗, 通過測距方程得到的過渡電阻辨識參數和故障距離估計曲線如圖10 所示。

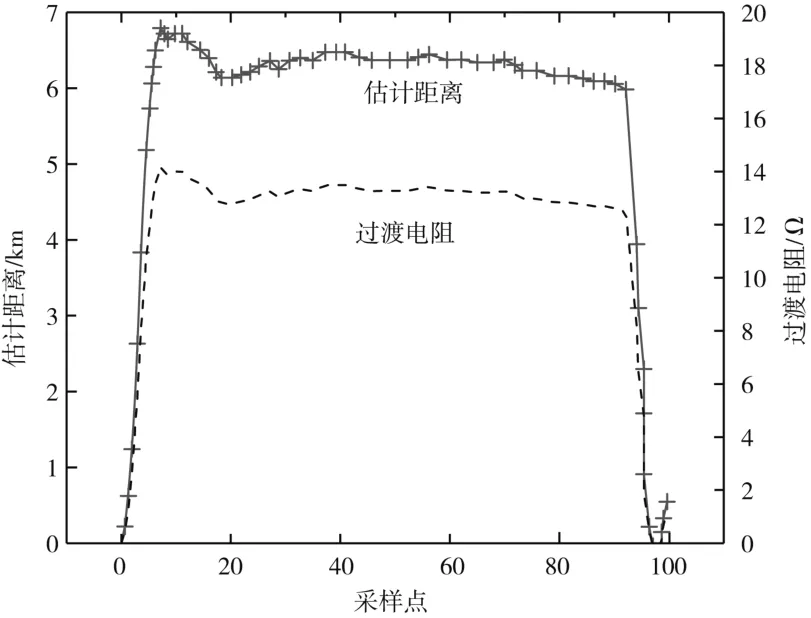
圖10 半周波故障的參數估計曲線

在不斷地移動數據窗口過程中, 故障狀態時的過渡電阻慢慢趨于一個恒定值, 并在小范圍內波動。將過渡電阻代入測距方程求解出故障距離, 其距離估計曲線如圖10 所示。在約20 個采樣點處估計距離達到6.2 km, 而后在±0.3 km 內波動, 過渡電阻在12.2 ～13.1 Ω 波動。定義故障距離估計值與真實值的相對誤差來評價算法的準確性:

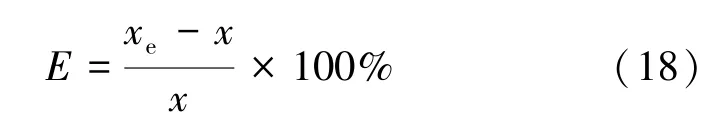
改變采樣頻率, 減少一個數據窗口的采樣點數量, 分別取每個數據窗口采集 5、10、15、20 個數據點, 算法的相對誤差曲線如圖11 所示。

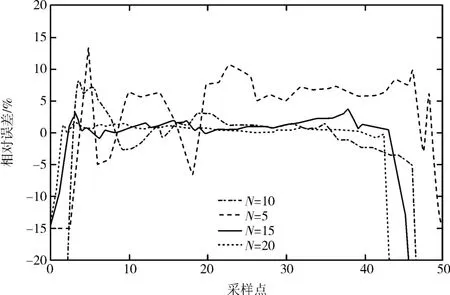
圖11 不同采樣點的相對誤差曲線

圖11 可以看出, 一個數據窗口內的采樣數量N越高, 算法的精確性與穩定性越好。在N＝10 時可以將相對誤差控制在±5%內, 在N＝20 時可以將相對誤差控制在±3%, 同時考慮到算法收斂時長應盡量較短, 在后續仿真實驗中可取N值為15。在其他條件不變的情況下, 設置不同的故障距離,觀察芯―護層接地故障下的電纜半周波、多周波早期故障下的故障點距離估計結果和相對誤差, 統計見表2。

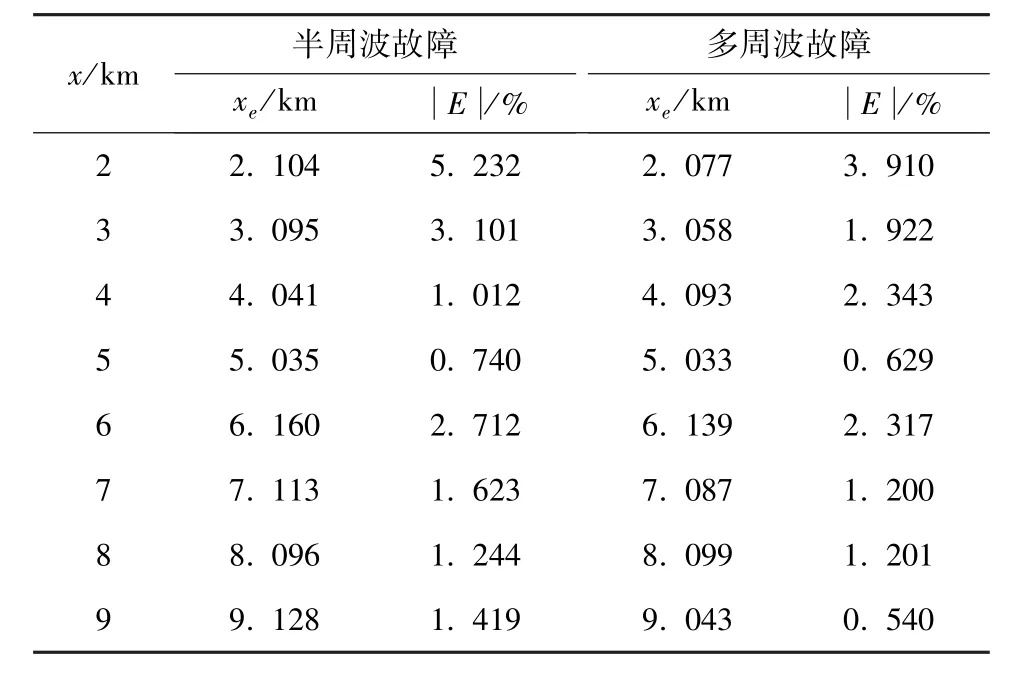
表2 芯―護層接地故障測距結果

改變電纜早期故障形式, 當電纜發生導芯―護層自恢復短路故障時, 在導芯和護層之間會產生電弧電壓, 線路參數和采樣頻率保持不變, 故障距離估計平均相對誤差由平穩數據窗下的估計值計算得到, 其結果見表3。

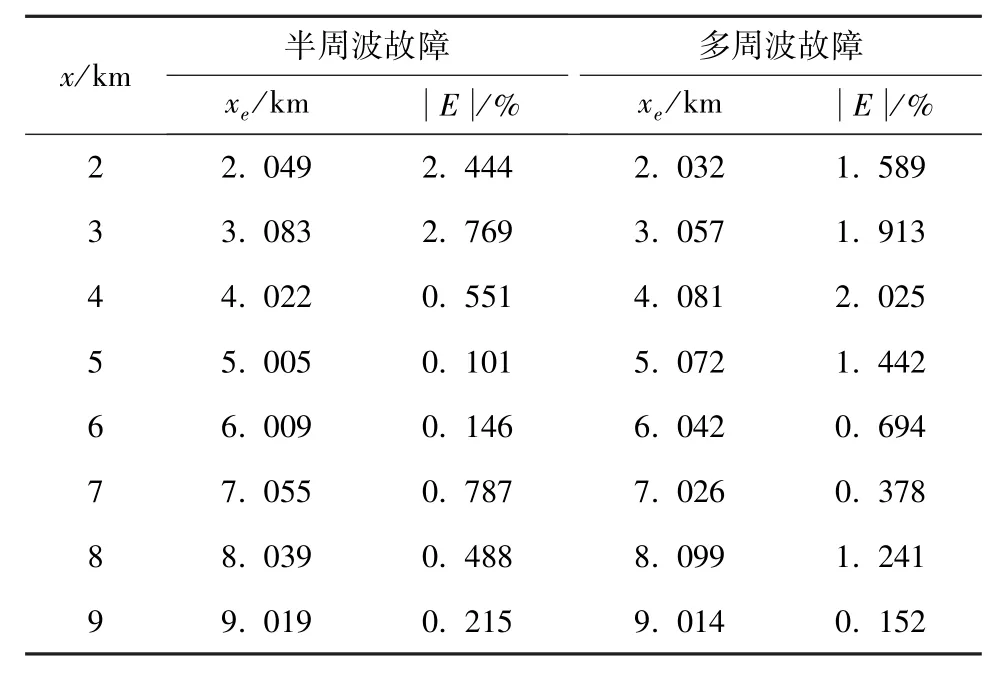
表3 芯―護層故障測距結果

從表2 和表3 可以看出, 無論是芯―護層接地故障還是芯―護層故障, 在其他條件不變時, 多周波早期故障因為暫態信號波形相較于半周波早期故障持續時間更長、更穩定, 易于監測設備提取信號至測距算法計算故障距離, 故多周波故障下的測距結果更好。隨著故障距離地不斷增加, 沿線傳播的暫態信號衰減嚴重, 此時兩種早期故障的識別率均會有不同程度的降低。

5 結論

針對現有地下電纜早期瞬時故障測距方法的不足, 本文考慮了電纜金屬鎧裝層與銅屏蔽層并建立不同故障狀態下的早期故障電路模型, 在參數辨識過程中以正弦逼近函數的精確求導來減小微分誤差并通過移動合適的數據窗返回故障點估計距離。通過PSCAD/EMTDC 仿真驗證了測距方法的可行性和有效性, 主要結論如下:

1) 所提測距方法在芯―護層接地故障和芯―護層故障兩種故障類型下, 不論半周波還是多周波故障形式下均具有良好的測距精度, 故障估計距離的相對誤差能夠控制在±3%內。

2) 當故障距離增大時, 由于暫態信號的衰減, 測距算法的表現有所下降, 但總體上多周波早期故障的測距結果優于半周波早期故障。

3) 對于復雜線路結構和多種形式噪聲干擾下的算法測距表現, 還需要進一步在現場實例數據中進行研究。