基于圖像熵的探地雷達Kirchhoff 偏移成像算法

林志強，王 磊，樊斌斌

（國防科技大學信息通信學院，武漢 430010）

0 引言

探地雷達（Ground Penetrating Radar，GPR）是利用寬頻帶高頻率電磁波脈沖的反射來探測地下介質結構和特性的一種地球物理探測設備［1-2］。探地雷達誕生于20 世紀初，隨著其技術的逐漸成熟，其應用領域逐步擴大，主要包括：考古探測、石油及礦產勘探、河流沉積物探測、堤壩和橋梁探傷以及地雷等爆炸物探測等。與其他物探技術相比，探地雷達的主要優點包括：分辨率高、探測快速、對目標的電磁特性敏感等［3］。

近年來，隨著探地雷達技術的深入發展，人們對其分辨率也提出了更高的要求，尤其是在軍事上要求探地雷達可以進行精確的目標識別，使得人們不得不在算法層面上尋求突破。合成孔徑成像是一類能夠有效改善探地雷達方位分辨率的方法，目前，常用的探地雷達合成孔徑成像算法有BP 成像算法［4］、頻率波數域F-K 偏移成像算法［5］、FDM 逆時偏移成像算法［6］、Kirchhoff 偏移成像算法［7］等。其中，BP 算法的算法復雜度最低，但成像精度略有欠缺；F-K 偏移算法具有精度高、穩定性好、運算速度快等優點，但難以適應變速介質；FDM 逆時偏移算法受地表陡傾結構的影響較小，但算法復雜度較高，運算速度較慢；Kirchhoff 偏移算法計算效率高，偏移歸位準確，但成像效果對波速變化比較敏感。

本文主要對傳統Kirchhoff 偏移算法進行了改進。通過引入圖像熵的概念，動態估計可使Kirchhoff偏移成像效果最好的波速參數，從而解決傳統Kirchhoff 偏移算法對波速變化敏感這一問題，為探地雷達快速、精確的成像提供一種新的方法支撐。

1 理論基礎

1.1 Kirchhoff 偏移成像理論

探地雷達Kirchhoff 偏移成像是一種基于電磁場波動方程積分解的成像算法［2］。在介質均勻的條件下，探地雷達發射電磁波的電場分量E（x，y，z，t）滿足標量波動方程：

式（3）說明P 點在t 時刻的波場值是由前一時刻t-r/v 地面上的場源激發的，這符合電磁波“向前”傳播的規律（惠更斯—菲涅爾原理），而探地雷達記錄的數據是地下目標反射至地面的波場函數值，探地雷達偏移成像的目的是利用記錄的數據反演出目標在地下的真實位置，這要依靠波“倒退”的規律。事實證明，波“倒退”也符合惠更斯-菲涅爾原理，也可以用Kirchhoff 偏移積分來描述，只是需要將時間“逆轉”，于是有：

1.2 圖像熵的基本概念

其中，“=”成立的條件是存在i∈{1，2，…，m}，j∈{1，2，…，n}，使得xij2=C 成立，此時圖像熵Q（X）取得最小值1。

通過上述分析可知，當圖像矩陣X 的能量取值越分散時，圖像熵Q（X）越大，反之，當圖像矩陣X的能量取值越集中時，圖像熵Q（X）越小。

2 改進的Kirchhoff 偏移成像流程

探地雷達采集的數據主要有A-scan 和B-scan兩種。A-scan 數據是探地雷達對某一探測位置進行掃描并錄取的一維單道數據，B-scan 數據是探地雷達沿某一測線方向掃描并錄取的二維數據。直觀上看，對探地雷達記錄的B-scan 數據進行Kirchhoff偏移成像的效果是把目標分散到各A-scan 數據中的能量進行匯集，從而提高目標的分辨率和信噪比。而這種目標聚焦，能量匯集的效果是與Kirchhoff偏移成像算法的波速參數密切相關的，波速參數與真實波速越接近，目標聚焦效果越好，反之，波速參數越偏離真實波速，目標聚焦效果越差。所以選取圖像熵來衡量Kirchhoff 偏移成像效果是比較合適的，同時可以通過不斷調節波速參數，來使Kirchhoff偏移成像效果達到最佳，并據此估計真實波速。

假設經過雜波抑制處理后的探地雷達B-scan數據圖像為D0，經過速度參數為v 的Kirchhoff 偏移成像處理結果為D（v），則本文所提基于圖像熵的探地雷達Kirchhoff 偏移成像算法的具體實施步驟如下：

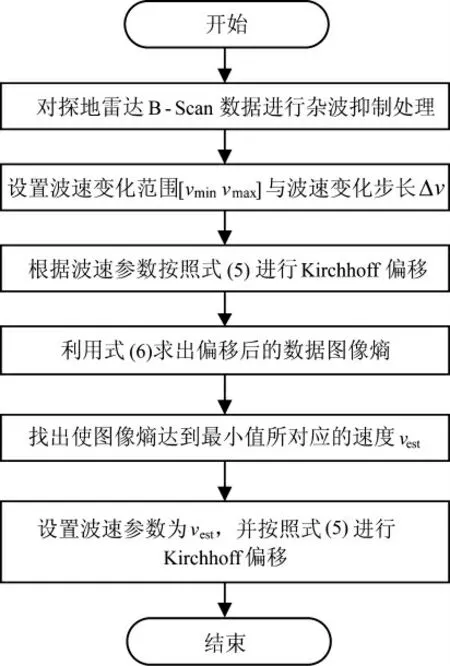
圖1 算法流程圖

3 仿真驗證

GPRMax 是一種利用有限差分時域（FDTD）方法模擬探地雷達數據的常用軟件。利用GPRMax 軟件產生仿真數據，仿真條件設置為：目標為直徑1 cm 的塑料小球，其相對介電常數為2.5，埋藏在水平位置2 m 地下10 cm 處，地表略微不平整，地下介質為干沙，其相對介電常數為6。脈沖探地雷達發射信號的波形為Ricker 子波，工作頻率設置為1 GHz。B-scan 數據的空間采樣間隔為0.5 cm，掃描道數為400，A-scan 數據采樣點數2 544，時窗6 ns。GPRMax軟件仿真的模型圖如下頁圖2 所示。對雜波抑制后的探地雷達B-Scan 數據成像如圖3 所示，可以看出目標回波在B-Scan 圖像中呈雙曲線形狀。

設置算法的波速參數變化范圍為：最大速度20 cm/ns，最小速度10 cm/ns，速度變化步長為0.1 cm/ns。根據算法求出每一個波速參數所對應的圖像熵，并繪制圖像熵隨波速參數的變化曲線，如圖4 所示。

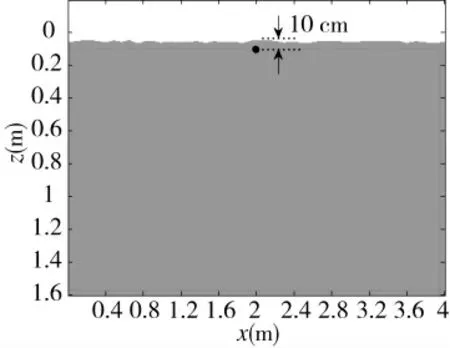
圖2 GPRMax 軟件仿真的模型圖

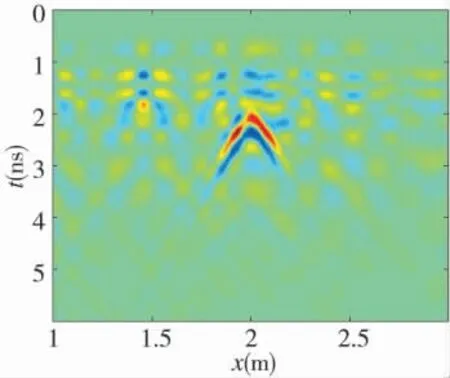
圖3 B-Scan 數據D0 成像

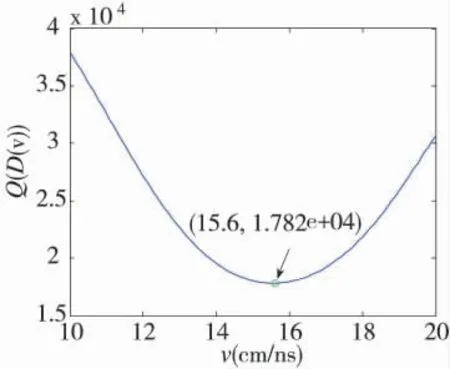
圖4 圖像熵變化曲線

根據圖像熵的變化曲線可知，當v=15.6 cm/ns時，圖像熵取最小值，也就是說根據本文所提算法估計的波速為15.6 cm/ns，依據此波速參數進行Kirchhoff 偏移成像得到的成像結果如圖5 所示。

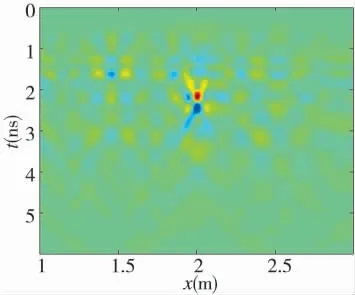
圖5 基于圖像熵的Kirchhoff 偏移成像結果

對比圖3 和圖5 可知，本文所提算法很好地使目標分散的能量匯聚到目標所在的真實位置，提高了目標的分辨率和信噪比，同時根據算法也較準確地估計了電磁波在地下傳播的速度。

本文仿真條件是均勻介質，在這樣的情況下，采用圖像熵的波速估計算法，能夠準確地估計出目標所埋藏位置處的波速，進而可以達到很好的成像效果。但在實際探地雷達應用過程中，地下介質可能是非均勻的，不同深度的介質其介電常數不同，這使得波速隨著深度略有變化。在這樣的情況下，如果原始的B-scan 數據經過雜波抑制處理后仍殘留有大量的雜波，甚至雜波的能量大于目標信號的能量，就會導致本文所提算法的成像效果下滑。這是因為圖像熵估計的是整個B-scan 數據進行Kirchhoff 偏移成像能量最集中時的波速，當雜波能量大于信號能量時，所估計出來的波速是雜波能量最集中時的波速，而雜波所在位置處的波速在非均勻介質情況下一般不等于目標所在位置處的波速。因此，為了使得本文所提算法在非均勻介質情況下也能夠得到不錯的成像效果，需要對B-scan 數據進行有效的雜波抑制，使得目標信號的能量大于或者遠大于雜波能量。

4 結論

本文首先研究了探地雷達Kirchhoff 偏移成像理論，分析了圖像熵性質和作用，然后基于此提出了一種利用圖像熵估計探地雷達波速參數，并進行Kirchhoff 偏移成像的算法，接著采用GprMax 軟件仿真的數據對算法進行了驗證，實驗結果表明，本文所提算法可以較準確地估計出地下電磁波的傳播速度，同時Kirchhoff 偏移成像也達到了很好的效果，最后，從理論上分析了在非均勻介質情況下，算法的成像效果與適用條件。