高壓共軌柴油機循環噴油量預測模型仿真研究

費紅姿， 屈超， 魏云鵬， 李瑞良

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

燃油系統的高壓共軌技術憑借更高的燃油噴射壓力、更快的響應速度以及更加靈活的燃油噴射策略為發動機滿足技術需求、實現綠色船用動力提供了有力支撐[1-2]。然而目前的高壓共軌系統對于噴油量控制的精確程度并不能滿足日益提高的技術需求。為此學者們提出了不同的解決方法，但是基于缸壓模型的燃油控制方法需要面對預測精度和傳感器等問題，而基于燃油系統壓力的噴油控制方案更具可行性。目前急需建立基于燃油系統壓力的噴油量精確控制實時預測模型[3]。

A.E.Catania 等[4]在研究中發現，壓力波動在沿噴油器、高壓油管向共軌傳播期間會受到燃油系統內機、電、液耦合的影響，使得能夠反映燃油噴射過程的波形產生變化；Schmid等[5]和Y.Shinohara等[6]直接在噴油器內部安裝了體積流量傳感器和壓力傳感器來監測噴油情況。直接在噴油器內部，尤其是盛油槽部位安裝傳感器可以最大限度的避免燃油系統對壓力波形的影響，較為直接地反映噴油情況；Catania等[7]通過燃油系統的結構參數計算燃油系統主頻，以分析噴油器入口處的壓力波動，但是沒有研究燃油系統不同位置的壓力波動及壓力波傳遞時的演化情況；Boudy等[8]和Han等[9]研究了不同的燃油物理性質對共軌內壓力波傳遞和單次噴射噴油量的影響，但也同樣沒有對壓力波傳遞時的演化特性進行研究；蘇海峰等[10]通過實驗測量共軌和噴油器入口的壓力，總結了壓力波對連續噴射的燃油噴射量波動的影響規律；白云等[11]通過建立高壓共軌噴油器功率鍵合圖數值模擬進行模擬實驗進而建立了循環噴油量波動回歸模型。

上述研究表明，壓力波動與實時噴油量信息密切相關，現有仿真模型雖然精度高，但計算速度慢，實時性差，無法實現發動機運行時在線實時輸出噴油量計算結果，無法用于實時控制。因而需要建立以軌壓變化為判斷依據實時計算噴油量的數學模型，用于系統的實時控制。本文通過建立高壓共軌柴油機的AMESim仿真模型，模擬不同工況下的噴油過程，研究了噴油量預測模型構建和模型參數辨識方法，在此基礎上對預測模型進行了優化，從而可以根據軌壓的變化實時預測噴油量。

1 高壓共軌系統仿真模型建立

高壓共軌系統由高壓油泵、共軌管、高壓油管、噴油器組成。本文針對某型高壓共軌系統建立了AMESim仿真模型，其基本技術參數如表1所示。圖1分別為高壓油泵、噴油器和共軌管的仿真模型。

表1 高壓共軌系統基本技術參數Table 1 Basic technical parameters of simulation model

為了驗證AMESim仿真模型的準確性，在軌壓為40、100、160 MPa時，噴油脈寬為0.18～2.48 ms的工況下，將實驗數據與仿真數據進行對比分析，如圖2所示。

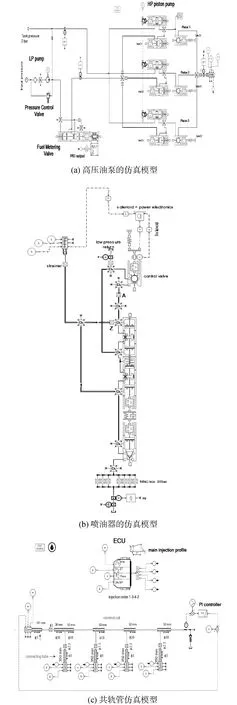
圖1 AMESim仿真模型Fig.1 AMESim simulation model

圖2 不同工況下實驗與仿真數據對比Fig.2 Data comparison of simulation and experiment at different work condition

從圖2中可以看出，3個軌壓下的仿真曲線與實驗值曲線總體變化趨勢一致。在160、100 MPa軌壓下，實驗與仿真數據誤差較小；40 MPa軌壓下，在1～2.25 ms有一定的偏差，最大偏差為9%。高壓共軌仿真模型與實際系統吻合度高，可以應用該模型進行研究。

2 基于瞬時軌壓的噴油量預測模型

2.1 噴油量與軌壓之間的關系

共軌管的燃油壓力波動反映噴油量信息，圖3為在軌壓為60 MPa，脈寬為1.8 ms時，柴油機的4個噴油器4次噴油下的壓力和噴油率波形。圖中可以看出，首先燃油在高壓油泵凸輪軸作用下被柱塞壓縮進入共軌管，引起共軌管軌壓上升，當柱塞達到上止點(即供油終點)時，停止供油；此時軌壓停止升高，在內部泄漏和脈動作用下，維持一定軌壓波動；然后ECU控制噴油器中的針閥開啟，在一定噴油脈寬作用下，將高壓燃油由噴油器噴入氣缸，引起軌壓快速下降，直至電磁閥關閉，針閥回位，噴油結束；軌壓停止下降，在內部泄漏和脈動作用下，維持一定軌壓波動，如此循環往復運行。

圖3 柴油機一個工作循環的壓力波動和噴油率Fig.3 Instantaneous pressure signal and injection rate in one working cycle of diesel engine

從圖3可以看出，在噴油時間內(虛線內)，軌壓快速下降，因此如何應用軌壓變化信息準確反映噴油量信息是本文研究的主要內容。

2.2 噴油量預測模型建立

為了建立軌壓波動與噴油量之間的關系，首先給出共軌管的燃油連續運動方程：

(1)

式中：Qpump為高壓油泵供進入共軌管的燃油體積流量；Qinj為噴油器的噴油率；Qleakinj為噴油器的燃油泄漏量。E為體積彈性模量；V為共軌管控制容積；p為共軌管內的瞬時壓力。

其中噴油器的燃油泄漏量Qleakinj可表示為：

Qleak=(0.1+Cleak)Qinj

(2)

式中：Cleak為系數項，可由實驗獲得。

在噴油過程中，供油量Qpump可以認為是零，并將式(2)代入式(1)可得：

(3)

式中：共軌管控制容積V可以表示為:

V=VCRP+VHPP1+VHPP2+VHPC+VCRC=

V′+VCRC

(4)

式中：VCRP為共軌管容積；VHPP1為高壓油泵與共軌管連接的高壓油管總容積；VHPP2為噴油器與共軌管連接的高壓油管總容積；VHPC為噴油器與高壓油管連接的高壓連接器總容積；VCRC為共軌控制容積補償量。VCRP、VHPP1、VHPP2和VHPC可以根據實際系統結構得到。

由于燃油在高壓下會造成共軌管及高壓油管形變，因此VCRC與壓力有關[12]：

VCRC=C1+C2P

(5)

式中：C1和C2為系數；P為共軌管的平均壓力。

通常情況下，根據燃油彈性模量的經驗公式，E與P相關，可由下式確定[13]：

E=1.2×104(1+0.001P)

(6)

將式(4)～(6)代入式(3)，得到：

(7)

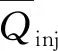
(8)

則燃油系統單次噴油量Vinj為：

(9)

式中：Δp≈-dp表示瞬時軌壓變化，在此定義為軌壓降。

式(9)為瞬時軌壓與噴油量之間的數學關系，亦即根據軌壓的變化，利用此模型可以實時預測高壓共軌系統的噴油量。在模型中，有兩個待定的參數C1、C2。本文基于AMESim仿真模型，在不同的工況下，對高壓共軌系統進行了仿真研究，辨識模型待定參數，從而得到不同工況下基于瞬時壓力的噴油量預測模型。

2.3 波形特征參數的處理

軌壓降Δp是預測模型中的關鍵參數，它的數值直接影響預測模型的準確度。圖4為1#噴油器噴射過程的軌壓波形在一個噴油周期內，可以將壓力變化過程定義為壓升段、波峰段、壓降段和波谷段。軌壓降Δp代表在壓降段軌壓的變化。由于壓力高頻波動，影響軌壓降Δp的取值。為此，將該波形進行小波去噪，得到平滑的反應壓力變化的波形曲線。將小波分解后壓力曲線的波峰段較為平滑的部分與波谷段的差值記為Δp。

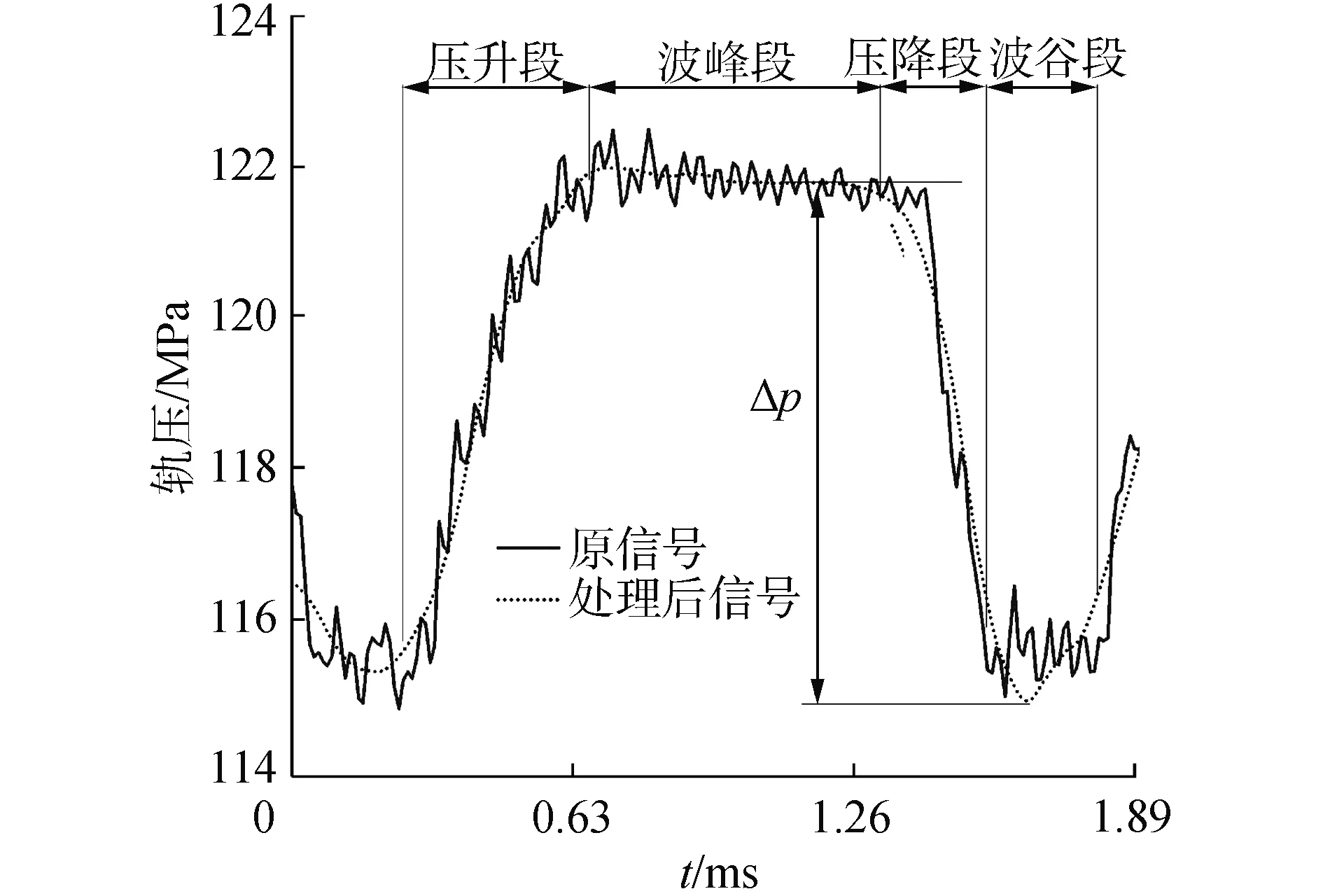
圖4 1#噴油器噴射過程的壓力波動Fig.4 Instantaneous pressure signal in 1# injector

2.4 模型特征參數辨識

圖5為在0.8 ms噴射脈寬下，不同軌壓下的軌壓降與噴油量對比。從仿真數據可以看出，在同一噴射脈寬下，噴油量與軌壓降變化規律一致性較好，因此，根據預測模型式(9)，本文建立了不同脈寬下的預測模型。

圖5 不同軌壓下的軌壓降與噴油量對比Fig.5 Pressure decline and injection volume with different the pressure of fuel

以噴油脈寬為0.8 ms的情況為例。固定噴油脈寬為0.8 ms，設定軌壓從40 MPa變化到140 MPa，對高壓共軌系統進行仿真，得到不同軌壓下對應的噴油量Vinj，同時計算對應的軌壓降Δp，如表2所示。根據實驗數據，得到CleakInj為0.035。將上述數據代入預測模型式(9)中，辨識出一系列待定系數C1和C2，然后求平均值，得到該脈寬下的預測模型。

表2 0.8 ms脈寬下仿真參數

噴油脈寬為0.8 ms時的預測模型為：

(10)

圖6為根據預測模型得到的噴油量預測值與仿真數據的對比曲線，可以看出，預測模型的預測值和仿真值變化基本一致。

圖6 噴油量預測值與仿真數據對比Fig.6 Comparison of predictive injection volume and simulation data

通過模擬仿真得到不同脈寬下的Vinj、Δp。按照上述方法，辨識出不同噴油脈寬下C1、C2值，從而得到基于軌壓波動的不同脈寬下噴油量的預測模型，如圖7所示。

從圖7中可以看出，基于本文提出的預測模型可以較準確的預測出不同脈寬下的噴油量，在0.6、0.8、1.0和1.2 ms小脈寬下，預測值準確度較高，噴油脈寬大于1.4 ms時預測值與仿真值趨勢一致，有一定誤差。

3 預測模型誤差分析與優化

3.1 預測模型誤差分析

圖8所示為預測模型誤差隨脈寬、軌壓變化的曲線。在噴油脈寬為0.6，0.8，1.0，1.2，1.4，1.6，1.8，2.0 ms時，預測模型的均方根誤差分別為0.63，0.81，3.22，0.72，4.44，8.53，5.12，6.75 mg。在小脈寬下預測模型的誤差值相對較小，當噴油脈寬超過1.4 ms時，均方根誤差較大。但是在大脈寬下噴油量也相對增加，因此，定義預測模型精度為準確度Ф：

(11)

式中:Vm為模型的噴油量預測值；Vt為噴油量仿真值。

在上述噴油脈寬下，計算預測模型的平均準確度，分別為87.65%、93.64%、88.93%、98.18%、90.58%、80.98%、92.20%、91.35%，如圖9所示。預測模型的平均準確度較高，但是個別預測值的準確度并不夠高，例如在軌壓為40 MPa時，噴油脈寬為1.0 ms的預測值準確度為76.11%。

3.2 預測模型的優化

從圖9各工況點的預測值與仿真值對比曲線中，可以看到低軌壓與高軌壓呈現出不同的變化規律，導致了預測值在部分工況點出現較大的偏差，這種現象在脈寬1.0、1.4、1.8和2.0 ms時更為明顯。為了進一步提高預測模型的精度，采用分段優化的方法，即將預測模型參數分成2段，低壓段40 MPa到90 MPa，超過90 MPa為高壓段。

對噴油脈寬為2.0 ms時的預測模型進行了分段優化，結果如圖10所示。從圖中可以看出，優化后低壓部分的預測模型誤差明顯減小，優化后預測模型的均方根誤差由6.75 mg降低到3.63 mg；平均準確度由91.35%提高到96.33%。利用同樣的方法對其他工況下的預測模型進行優化。

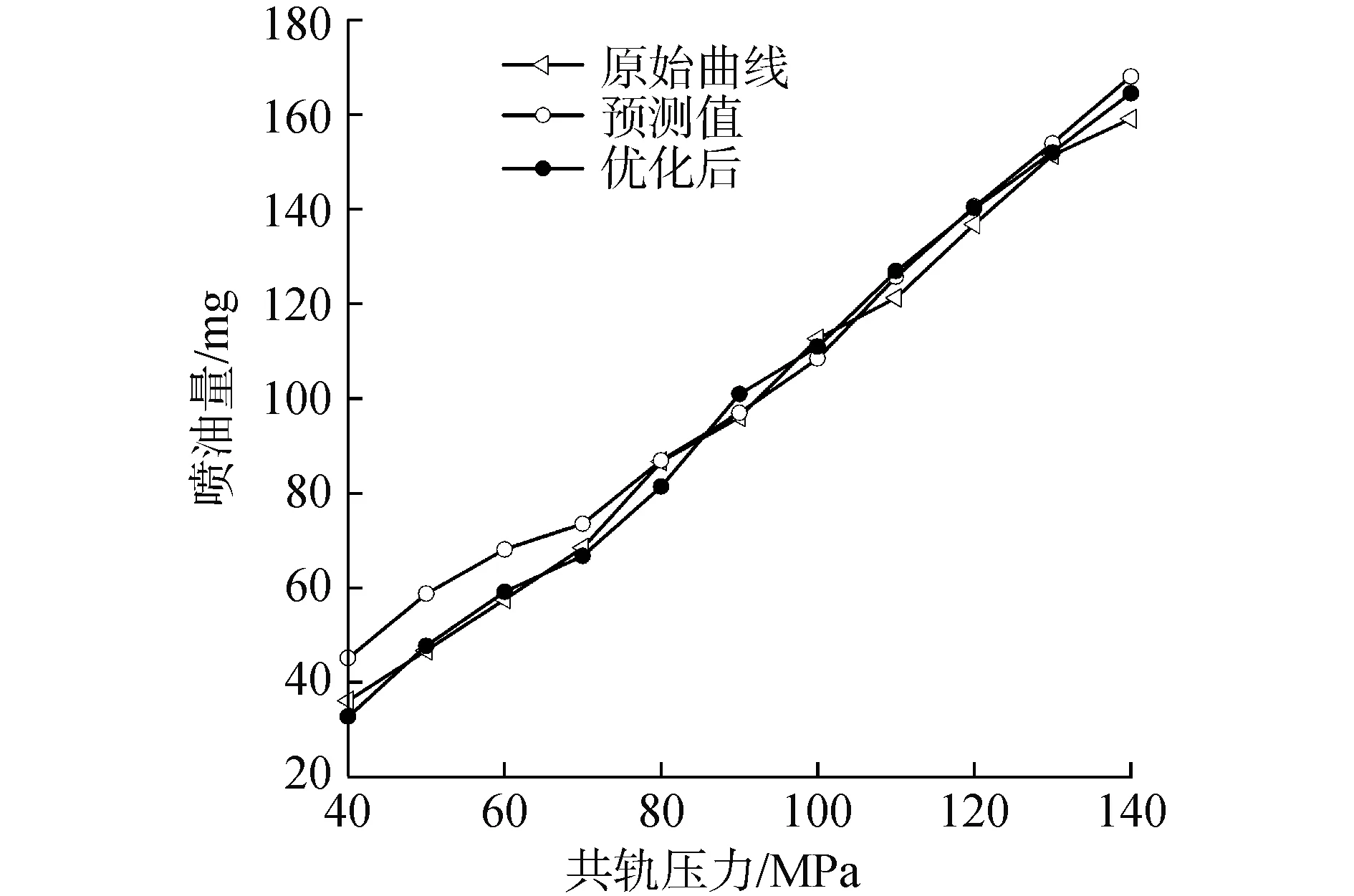
圖10 優化前后的對比曲線Fig.10 Comparison curves before and after optimization

4 結論

1)通過分析瞬時燃油壓力與噴油率之間的變化關系，提出了基于燃油壓力波動動態規律建立噴油量預測模型的方法。基于共軌管的燃油連續運動方程，通過簡化影響噴油量的共軌管控制容積表達式，得到了在噴油時間內，循環噴油量預測線性數學模型。

2)應用高壓共軌系統仿真模型，模擬不同工況點下的噴射過程，根據同一噴油脈寬下軌壓的變化對預測模型參數進行了辨識，得到了一系列不同噴油脈寬下的噴油量預測模型，該模型可以根據共軌壓力的瞬態變化預測不同噴油脈寬下的噴油量。

3)對預測模型進行誤差分析，在8個噴油脈寬下的模型預測準確度在80%以上，平均準確度為90.43%，最小誤差值僅為0.007 mg。為了進一步提高預測模型的精度，采用分段優化的方法，將預測模型參數分成低壓段和高壓段，優化后低壓部分的預測模型誤差明顯減小，優化后，預測模型的均方根誤差由6.75 mg降低到3.63 mg；平均準確度由91.35%提高到96.33%。