基于幾何參數標定的串聯機器人精度提升

趙藝兵, 溫秀蘭, 喬貴方, 呂仲艷, 宋愛國, 康傳帥

(1.南京工程學院 工業中心 創新創業學院, 江蘇 南京 211167； 2.南京工程學院 自動化學院,江蘇 南京 211167； 3.東南大學 儀器科學與工程學院,江蘇 南京 210096)

1 引 言

我國于2017年啟動實施“智能機器人”重點專項計劃[1],指出工業機器人應用于高端制造領域時,其絕對定位精度應優于 0.05 mm,姿態角應優于0.1°。目前,盡管工業機器人的重復定位精度較高,能滿足示教編程的需求,但絕對定位精度還較低,難以滿足機器人在精密加工、精密檢測、精準醫療等高精尖制造業的迫切需求。通過對機器人實測標定可以有效提高機器人末端定位精度。標定通常分為以下3級：一級標定也稱為關節級標定,主要是對驅動器和關節傳感器機構的運動學進行標定,其目的是確定關節位移傳感器產生的信號和關節實際位移之間關系；二級標定也稱為機器人幾何參數標定,即確定機器人的幾何參數模型與機器人關節角之間關系；三級標定也稱為非幾何參數標定,非幾何參數誤差主要包括關節柔度、摩擦、間隙及連桿變形等。大量研究結果表明：影響機器人作業精度的主要誤差源于幾何參數誤差,占到總誤差的80%～90%,通過對機器人幾何參數標定能夠在不改變硬件結構或控制器前提下通過校正軟件快速實現機器人絕對定位精度提升[2～4]。

機器人幾何參數標定包括建模、測量、辨識及補償4個過程。機器人建模是標定的基礎,目前最常用的幾何參數模型是基于齊次變換矩陣的DH模型,該模型首先在機器人的每個連桿上建立一坐標系,利用相鄰連桿間變換矩陣計算得到末端執行器的位置和姿態。因該模型連桿坐標系原點位于關節軸線與關節軸線公法線的交點,當兩軸線平行或垂直時軸線的微小變化會導致機器人幾何參數變化很大甚至到無窮,不滿足機器人標定時要求模型具有連續性要求,模型存在奇異性,影響標定結果的準確性。為了解決該問題,Hayati S A提出了改進的DH模型(MDH模型)[5],當相鄰關節軸線平行時增加一個旋轉參數,彌補了DH模型的不足；但當相鄰兩軸線垂直或接近垂直時,該模型仍具有奇異性,影響機器人標定的準確性[6]。為滿足標定模型具有完備性與連續性要求,文獻[7]在DH法建立的桿件坐標系上研究了6參數串聯機器人的誤差模型。文獻[8, 9]研究了通過建立指數積模型對串聯機器人幾何參數進行標定,取得較好效果。辨識是從測量數據中獲取機器人實際模型參數信息的過程,辨識結果的準確性直接影響其定位精度。傳統的辨識方法有最小二乘法、Levenberg-Marquardt算法、卡爾曼濾波法等。近些年智能計算得到長足發展,先后出現遺傳算法、免疫進化計算、微分進化、螞蟻算法、粒子群算法等,已有學者嘗試將智能計算應用于對機器人幾何參數標定取得了較好效果[10～14]。文獻 [10]建立了6自由度機器人的MDH模型,通過計算種群的適應值按照賭輪法選擇個體,根據事先設定的概率進行交叉和變異操作,通過仿真驗證算法的有效性。文獻[11]將粒子群優化算法用于對神經網絡初始權值和閾值優化,實現機器人綜合精度補償,用來提高飛機自動化裝配精度。文獻[12]采用擴展卡爾曼濾波對機器人幾何參數辨識,采用人工神經網絡對連桿變形、關節柔性、齒輪間隙等無模型的非幾何參數誤差進行補償來提高PUMA和HH800機器人精度。文獻[13]研究了基于量子粒子群優化算法的機器人幾何參數標定方法,選用五軸并聯機床的平面約束機構為試驗對象驗證了算法的有效性。文獻[14]采用深度神經網絡辨識機器人非線性殘余誤差,通過現場優化機器人焊接軌跡實驗來驗證算法的有效性。

針對機器人相鄰兩軸線垂直及接近垂直時,常用DH模型、MDH模型存在奇異性,本文研究建立了串聯機器人的零參考模型,該模型其零位可以任意選取,基于位置相似性原理,通過遞歸方程計算獲得末端位姿封閉形式的解,非常適用于關節臂依次相連的串聯機器人。根據該模型標定機器人幾何參數誤差特點,提出了基于改進遺傳算法實現機器人幾何參數標定,以提高機器人定位精度。

2 機器人幾何參數標定的數學模型

2.1 零參考模型

建立串聯機器人的零參考模型(zero reference model,ZRM)如圖1所示。Oxyz為機器人基坐標系,ηi為機器人方向矢量,ρi+1為連接矢量,i=1,2,…,n,n為機器人關節數目。機器人零位時的方向矢量和連接矢量表示為η0i和ρ0i+1,即為機器人的名義幾何參數,可從機器人手冊中獲得。

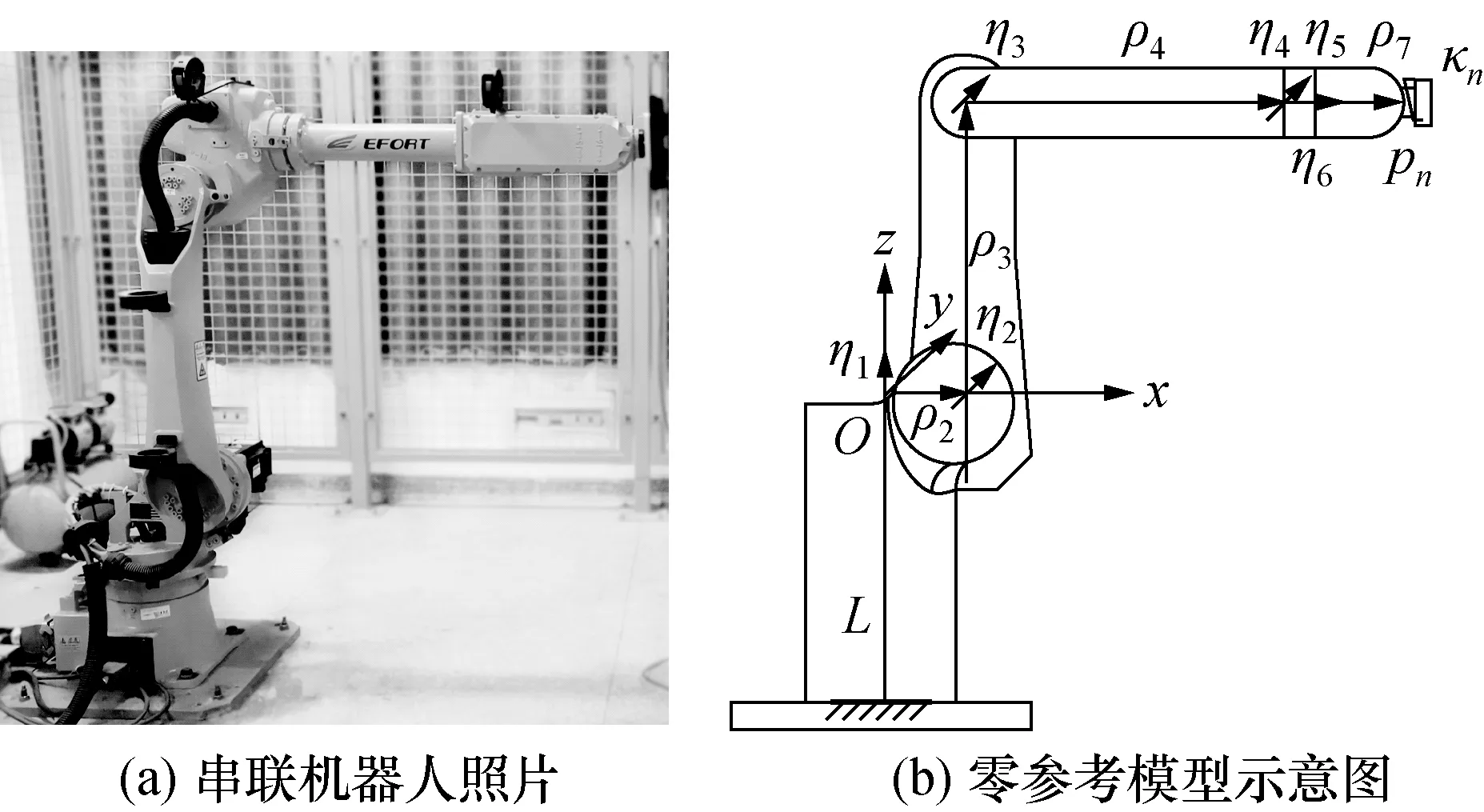
圖1 零參考模型Fig.1 Zero reference model

任意位置時的ηi,ρi+1與η0i,ρ0i+1具有如下關系:

ηi=κiη0i,ρi+1=κiρ0i+1

(1)

式中：κi為串聯機器人的旋轉矩陣[15],可表示為

(2)

其中，矩陣R(qi,η0i)表示關節角qi繞軸線η0i旋轉,計算公式為：

R(qi,η0i)=

其中,Vi=1-cos(qi),Si=sin(qi),η0ix,η0iy,η0iz分別表示η0i在x,y,z方向的分量。

2.2 標定模型

具有n個旋轉關節的串聯機器人其末端姿態和位置可由旋轉矩陣κn和平移矩陣Pn表示為[16]：

(3)

(4)

由式(3)和式(4)可見,κn和Pn是關節角qi及機器人幾何參數η0i和ρ0i+1的函數,當機器人零位狀態的方向分量沿x,y,z軸有微小誤差δη0ix,δη0iy,δη0iz時,引起R(qi,η0i)的誤差為δR(qi,η0i)：

δR(qi,η0i)=κxiδη0ix+κyiδη0iy+κziδη0iz

(5)

誤差δR(qi,η0i)將引起機器人末端姿態旋轉矩陣κn產生誤差δκn,可表示為:

(6)

由幾何參數誤差δη0i、δρ0i+1引起的機器人末端位置變化為

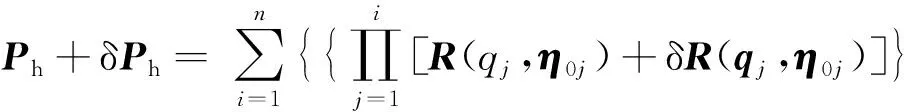
[ρ0i+1+δρ0i+1]}

(7)

由式(6)和式(7)可知,若存在幾何參數方向分量誤差δη0ix、δη0iy、δη0iz及連接分量誤差δρ0i+1x、δρ0i+1y、δρ0i+1z,則導致末端姿態及位置發生變化δκh和δPh。

設由機器人名義幾何參數經公式(3)和公式(4)計算得到末端姿態和位置的名義旋轉和平移矩陣分別為κhn和Phn,根據激光跟蹤儀測得末端在基坐標系下繞x、y、z軸的姿態坐標及沿x、y、z軸的位置坐標求得末端姿態和位置的測量旋轉矩陣κhm和平移矩陣Phm,則末端姿態和位置的旋轉誤差矩陣δκh和平移誤差矩陣δPh計算如下[17]：

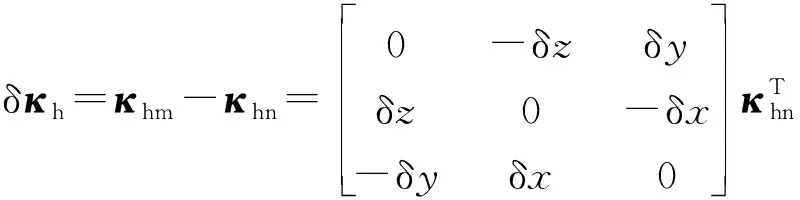
由幾何參數誤差引起機器人末端姿態和位置變化的關系式可表示為[16]:

(8)

其中Je為 (6+n)行6n列Jacobian矩陣,

δη0=[δη01xδη01yδη01z… δη0nx]T,

δρ0=[δρ02xδρ02yδρ02z… δρ0n+1x]T。

2.3 目標函數

采用IGA優化搜索機器人幾何參數誤差時,定義其目標函數f為：

(9)

(10)

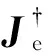
由此可見,目標函數f是幾何參數誤差[δη01xδη01yδη01z… δη0nx, δρ02xδρ02yδρ02z… δρ0n+1x]的函數,機器人幾何參數標定實質是通過優化算法搜索一組幾何參數誤差集,使末端位姿誤差為最小,屬于多變量復雜優化問題,非常適合用改進遺傳算法來求解。

3 改進遺傳算法實現幾何參數標定

3.1 編碼

采用遺傳算法優化搜索機器人幾何參數誤差旨在找到目標函數最小值,從而提高機器人末端定位精度。考慮到幾何參數誤差標定待優化變量多,且數值連續,為提高優化精度和效率,采用實數編碼,每一個基因代表一個待優化變量,所有變量對應的基因依次連在一起構成該實數編碼的個體。

設優化問題為最小化問題：

(11)

式中：f為目標函數；S=(s1,…,sl,…,sp)表示一個個體,其中sl(l=1,2,…,p)為待優化變量,p為優化變量的數目；al、bl分別為變量sl的上下界。

如圖1所示6自由度串聯機器人,待優化個體S表示為6個關節的幾何參數誤差集[δη01xδη01yδη01z… δη06z, δρ02xδρ02yδρ02z… δρ07z],采用IGA同時搜索上述幾何參數誤差,完成標定。

3.2 交叉操作

考慮到機器人ZRM幾何參數標定其目標函數中待優化變量不僅彼此獨立,而且變量數值均較小,因此采用混合交叉策略(BLX-α)[18],算法如下：

(1)從種群中隨機選取兩個父代個體S1、S2；

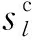
(12)

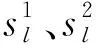
3.3 機器人幾何參數標定流程

為保持群體多樣性,IGA實現時采用基于代溝最小的代選擇模型,具體步驟如下：

step 1.設置進化代數t,隨機產生M個初始個體,構成初始種群；

step 2.從群體中任意選取兩個個體S1、S2作為父代；

step 3.將S1、S2采用BLX-α交叉產生nc個子群體；

step 4.計算S1、S2和nc個子群體的目標函數值；

step 5.從S1、S2和nc個子群體中選擇目標值最小的兩個個體替換原父代S1、S2；

step 6.判斷是否滿足終止條件,若不滿足,則t=t+1,轉Step 2；否則輸出優化所得幾何參數誤差；

step 7. 根據優化得到的幾何參數誤差誤差計算標定前后機器人末端絕對位置和姿態誤差。

4 實驗與結果

4.1 仿真實驗

4.1.1 位姿產生

6自由度串聯機器人在工業中應用最多,為了驗證算法的有效性,選擇圖1所示ER10L-C10的6自由度串聯機器人作為實驗對象,從使用手冊中獲取該機器人零參考模型名義幾何參數見表1。

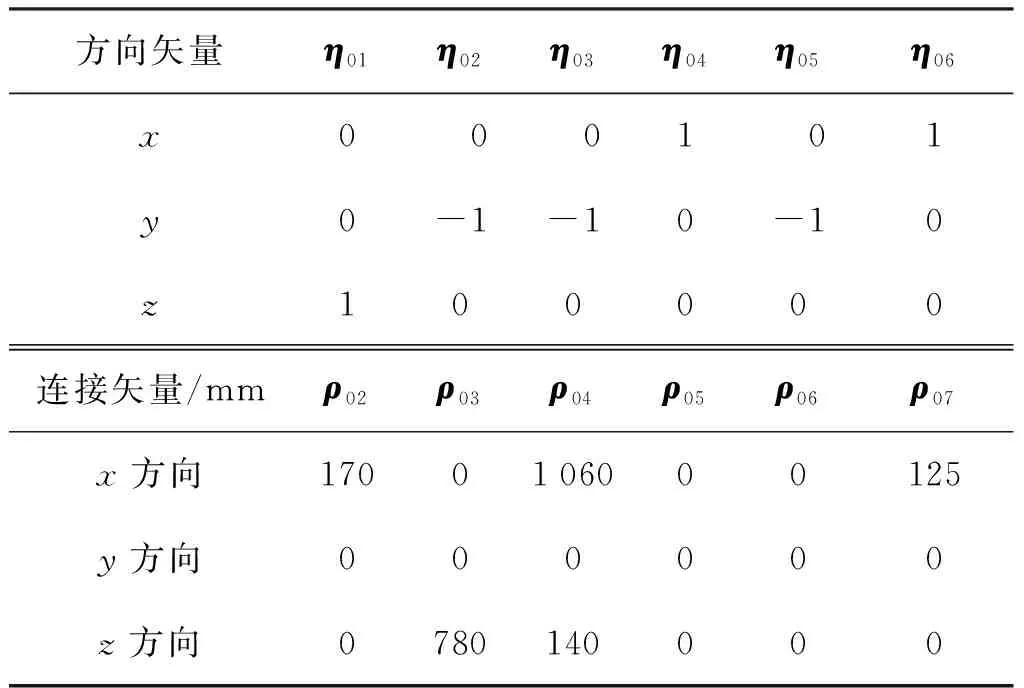
表1 ER10L-C10機器人名義幾何參數Tab.1 Nominal geometric parameters of ER10L-C10 robot

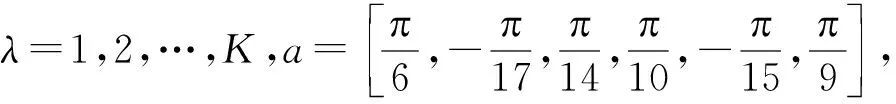
考慮到因機器人加工、裝配、磨損等誤差會導致由機器人示教器設定的關節角與實際關節角間存在誤差,實際關節角產生為在名義關節角上加入±0.001 rad均勻隨機噪聲。由關節角及幾何參數的名義值和實際值根據第2.2節公式即可計算出機器人末端姿態和位置的名義值、實際值及姿態與位置誤差。考慮到在測量機器人末端位姿時存在測量誤差,在由上述公式計算獲得的末端姿態和位置實際值上分別加入均值為計算值,方差為0.01 rad和0.5 mm的正態分布隨機誤差,得到末端姿態與位置的測量仿真值。

4.1.2 實驗結果

根據上述隨機設定的幾何參數誤差和關節角,采用提出的IGA優化求解機器人幾何參數誤差,其中種群和子代種群規模均設定為10,算法終止條件設定為最大進化代數1000。在Intel(R) Core(TM)i5-4570 CPU主頻3.20 GHz計算機上采用Matlab R2015b在設定的標定點N=4,8,16,32,48,64等6組不同關節角下完成1000代進化所需時間分別為 78, 145,280,546,830,1140 s。圖2同時繪制了N=4,8,16,32時的進化過程圖,表2給出了在上述設定的不同組關節角下機器人末端位置和姿態標定前后誤差比較結果,其中AOE為平均絕對姿態誤差,為平均絕對位置誤差,MOE為最大絕對姿態誤差,MPE為最大絕對位置誤差。

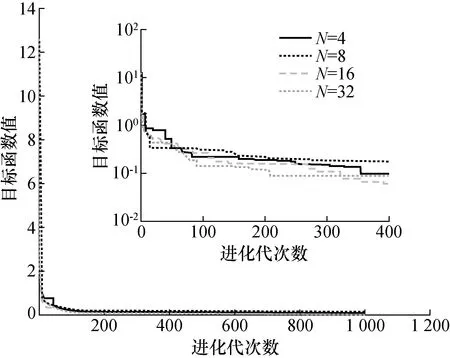
圖2 進化過程圖Fig.2 Evolution process figure

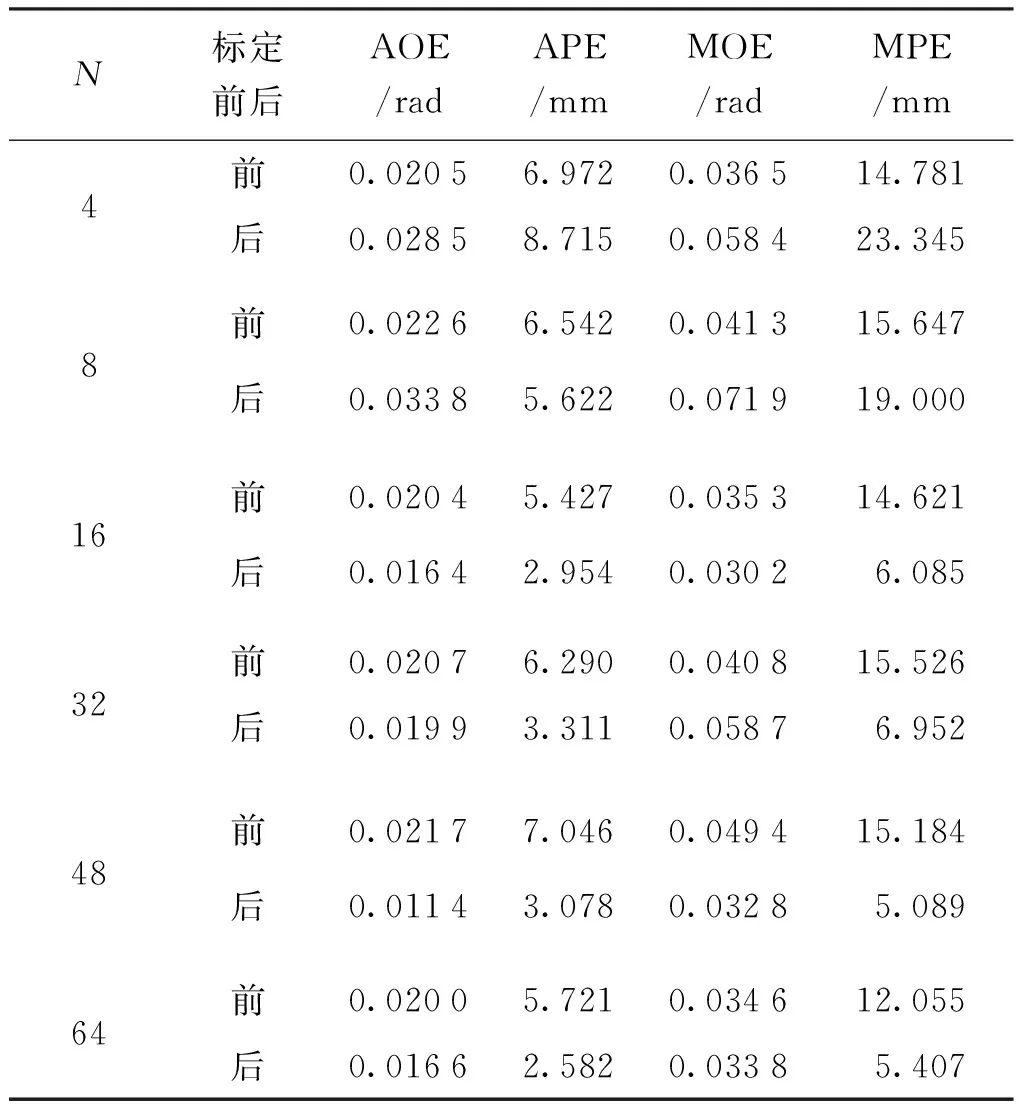
表2 預先設定誤差與標定后誤差比較Tab.2 Comparison between the pre-assumed and post-calibrated pose errors

由圖2和表2可見,提出的IGA能夠快速完成機器人ZRM幾何參數標定,機器人在設定的不同標定點下其末端定位精度均有大幅提升。為了驗證經標定后的機器人其精度提升的泛化能力,針對設定的6組標定點,分別在機器人整個工作空間內隨機產生40組關節角,根據不同標定點下優化得到的機器人幾何參數值計算末端測試點在標定前后位置誤差見表3。

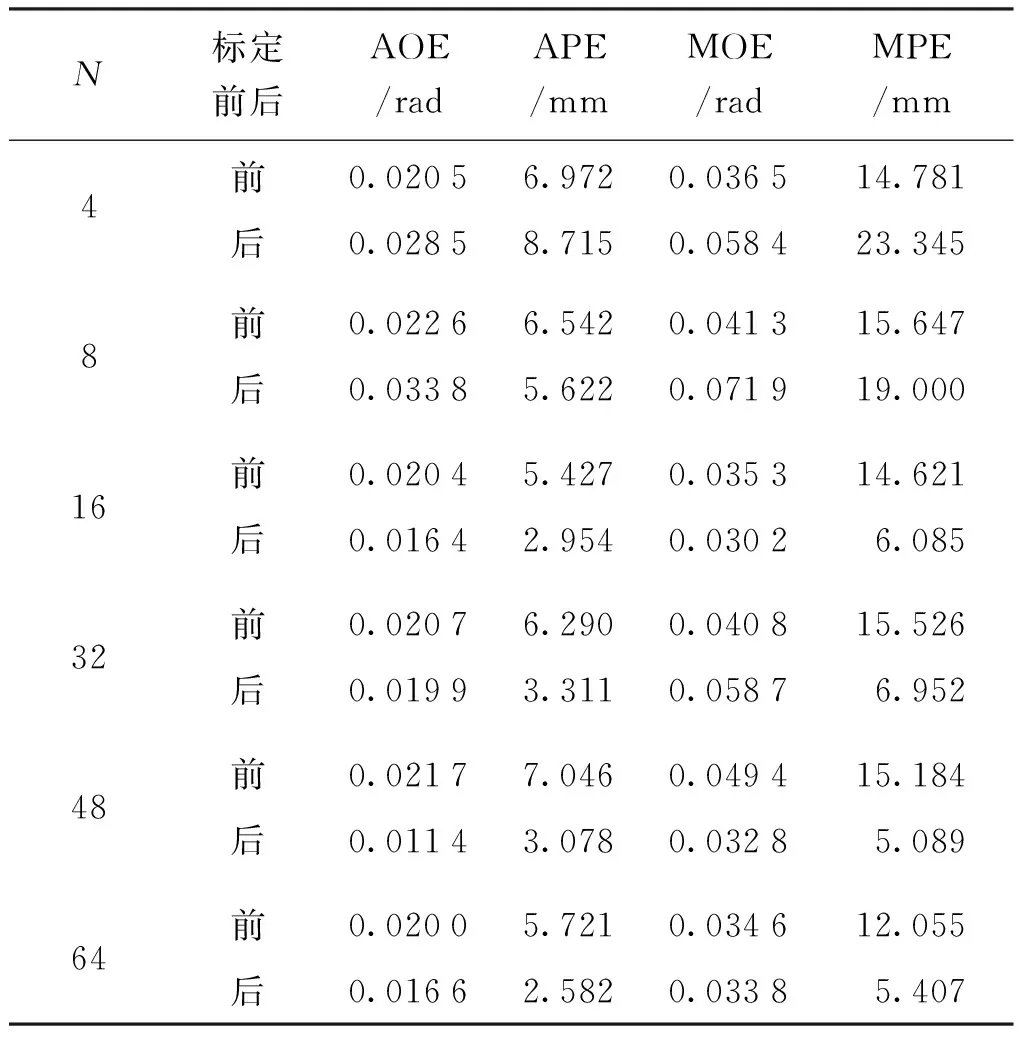
表3 整個工作空間內誤差比較Tab.3 Errors comparison in the whole workspace

由表2和表3可見,在標定點N為4和8時,盡管標定效果很好,但隨機產生的測試點精度提升效果差,隨著N增加,測試點精度提升效果逐步改善,當標定點取為48時,其測試點平均和最大絕對定位誤差由標定前的7.046 mm和15.184 mm分別改善為標定后的3.078 mm和5.089 mm,精度提升效果最佳；當標定點進一步增加時精度提升效果趨于穩定。因此,在對機器人實測標定時建議標定點設定為50個左右為宜,隨機產生的測試點其精度提升泛化能力強。圖3給出了N=32和N=48時,測試點標定前后絕對位置誤差的結果對比。

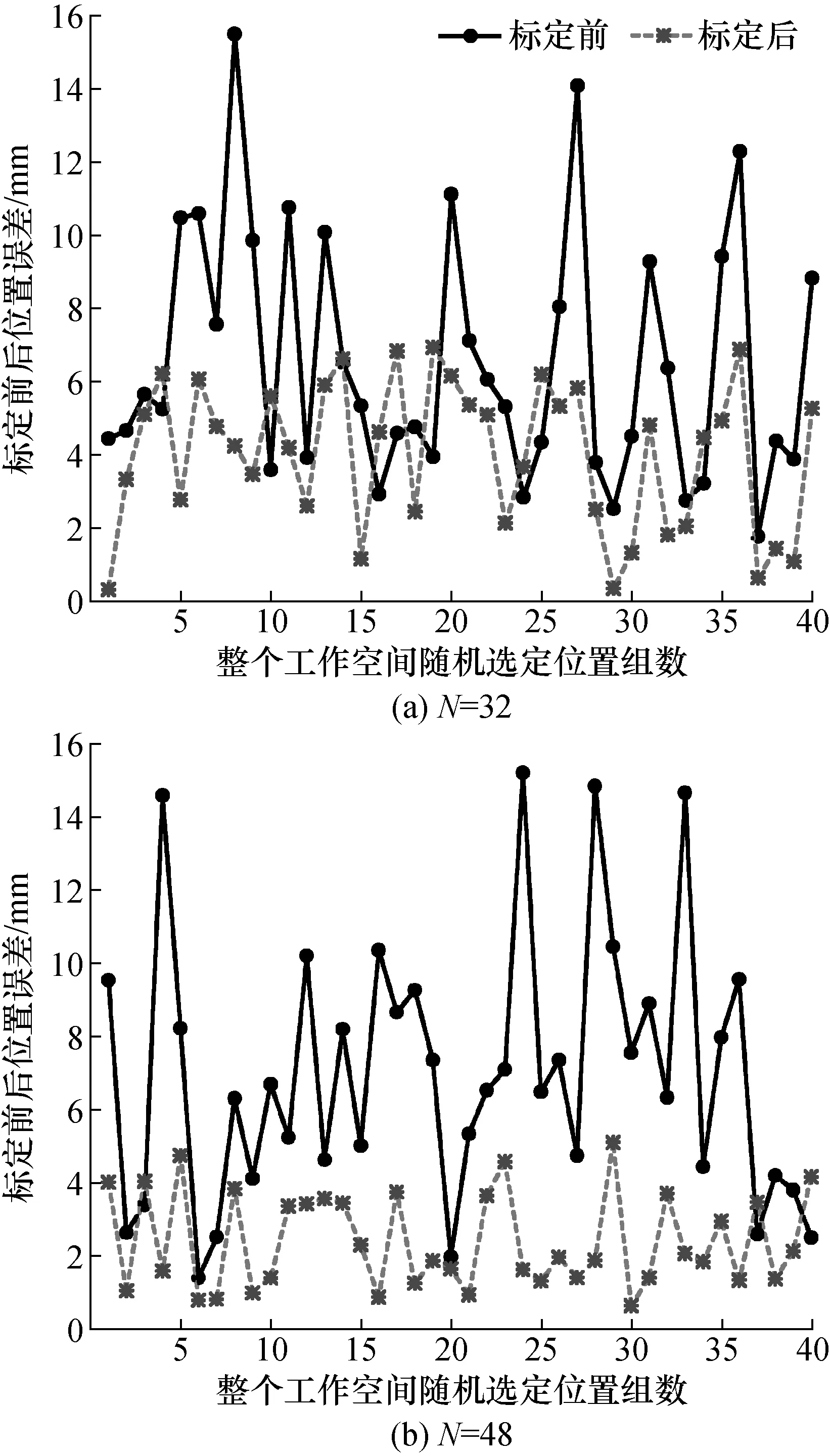
圖3 仿真測試點位置誤差比較Fig.3 Position errors comparison of simulation test points

4.2 實測標定

對實驗室ER10L-C10機器人標定實測環境如圖4所示,該機器人末端負載為0～10 kg,重復定位精度為±0.05 mm,測量由Leica AT960激光跟蹤儀、TMAC探測器、上位機及Spatial Analyzer(SA)軟件共同完成,TMAC安裝在機器人末端的法蘭上,Leica AT960空間測量精度為15 μm+6 μm/m,能夠同時測量機器人末端的位置和姿態,對溫度、濕度及壓力的變化具有自檢和補償功能。測量過程嚴格按照ISO 9283即GB/T 12642-2013[19]工業機器人性能規范及其試驗方法標準執行。

圖4 ER10L-C10標定實測環境Fig.4 Real measurement setup for ER10L-C10 calibration

在SA軟件中設置機器人的基坐標系為參考坐標系,以坐標值(1 300, 0, 900)為中心點,在邊長1 500 mm的正方體工作空間內隨機生成50個標定點的末端位置和姿態及對應的關節角,采用提出的IGA方法對ER10 L-C10幾何參數誤差進行標定,其中方向分量誤差和連接分量誤差分別在[-0.01,+0.01]和[-0.5,+0.5]區間內均勻隨機產生,計算標定前后的絕對位置誤差如圖5所示,其最大和平均絕對位置誤差由標定前的8.683 5 mm和5.579 1 mm分別降為標定后的1.368 3 mm和0.376 4 mm,定位精度有大幅提升。

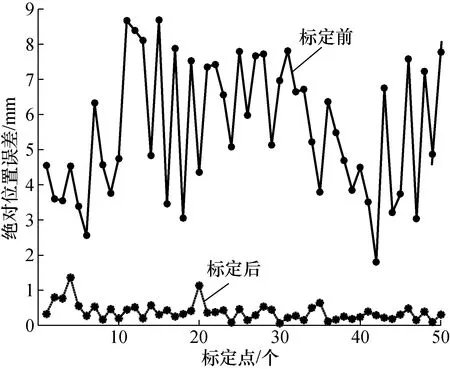
圖5 ER10 L-C1050個標定點絕對定位誤差Fig.5 APE of 50 calibration points for for ER10L-C10

為了驗證經標定后機器人精度提升的泛化能力,在上述正方體工作空間內重新隨機生成100個測試點,用已標定好的幾何參數計算測試點標定前后的絕對位置誤差如圖6所示,由圖可見,測試點最大和平均絕對位置誤差由標定前的8.931 7 mm和5.917 2 mm分別降為標定后的1.213 7 mm和 0.452 7 mm, 平均定位精度提升了92.3%,證實了提出方法對隨機產生測試點精度提升泛化能力強。

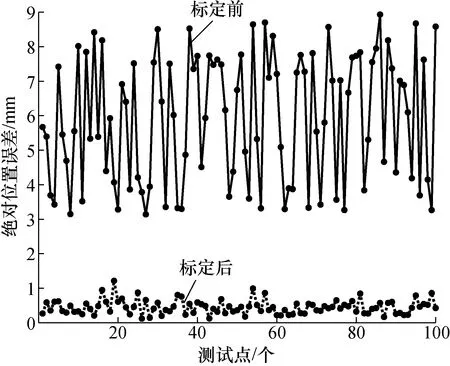
圖6 ER10L-C10100測試點絕對定位誤差Fig.6 APE of 100 test points for for ER10L-C10

5 結 論

針對當機器人相鄰兩軸線垂直及接近垂直時常用模型存在奇異性問題,建立了包含方向矢量和連接矢量的串聯機器人零參考模型,提出了用改進遺傳算法優化求解零位方向分量和連接方向分量,大量實驗結果表明：(1) 所建機器人零參考模型滿足標定模型連續性要求,避免奇異點出現；(2) 對機器人進行幾何參數標定時,標定點數取為50點左右最為適宜,標定效果最佳；(3) 對ER10L-C10機器人,采用提出的IGA對其ZRM幾何參數誤差標定后,該器人在整個工作空間內末端定位精度平均提升約90%,適于在有高精度定位要求的串聯機器人幾何參數標定中推廣應用。