基于蒙特卡羅方法的水體光場傳輸特性研究?

（海軍駐武漢地區(qū)第七軍事代表室 武漢 430223）

1 引言

進入21世紀，隨著經濟和技術的快速發(fā)展，對海洋的研究已經成為一個新的領域。海洋資源開發(fā)、海洋自然環(huán)境保護以及海洋軍事應用等方面的研究越來越引起人們的關注［1］。

光電探測成像技術是海洋探測及環(huán)境保護的重要手段之一。然而，光在水下傳播過程中，受到水分子和其他懸浮粒子的作用，將發(fā)生吸收和散射現象，使得光線能量逐漸衰減，且成像質量急劇下降。因此，對水下光場傳輸特性的研究具有重要的意義［7］。

研究水下光場傳播規(guī)律的主要方法有幾何光學方法、輻射傳輸方程方法［3］和蒙特卡羅模擬方法等［4～5］。幾何光學方法主要是采用光在水空界面的折射定律和光在純凈水中的直線傳播規(guī)律，無法深入研究散射背景條件下的光傳播特性。輻射傳輸方程雖然可以描述光在強散射水體中的傳播特性，可詳細地考慮散射、吸收、輻射等光與物質相互作用的現象，但是對于復雜邊界條件和初始條件下方程求解比較困難。而蒙特卡羅模擬方法［6～9］作為研究散射介質中光傳輸特性的一種適用廣泛而嚴謹的方法。本文基于該方法仿真分析了在強散射背景條件下水體的光場傳輸規(guī)律。

2 方法

光子在水體中的傳播規(guī)則采用概率分布來描述。如圖1是蒙特卡羅方法水體散射仿真流程圖，單個光子首先被初始化統一權重，設置光子步長，并在坐標系中移動它。

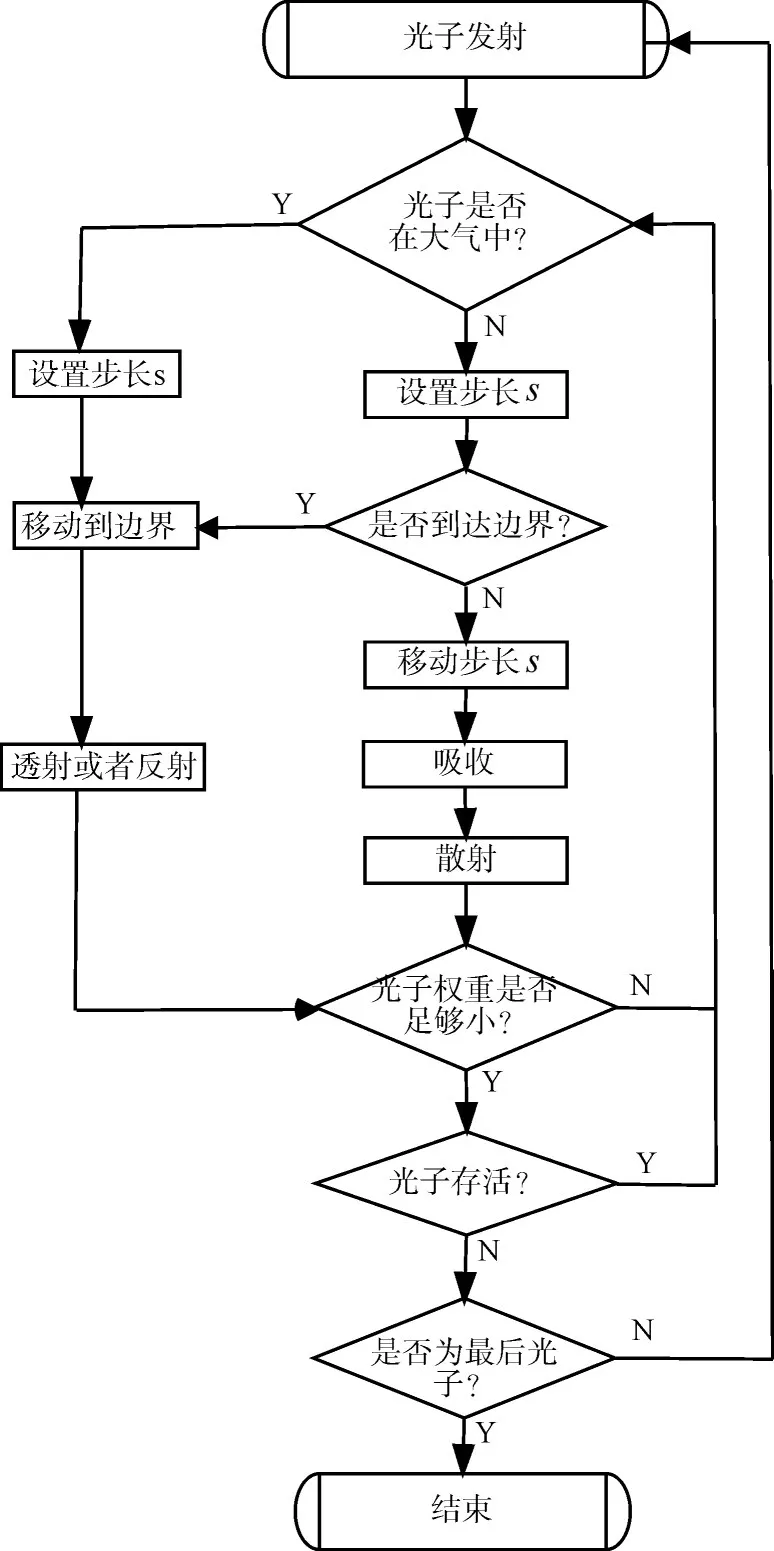
圖1 蒙特卡羅方法水體散射仿真流程圖

若光子到達水體邊緣，檢查其內部反射的幾率，并決定其是繼續(xù)留在水體內還是離開水體。若其在內部反射，則需修改其運動方向，繼續(xù)運動；否則，光子離開水體，記錄為反射（透射）。在每運動一個步長，計算光子由于水體的吸收造成的權重衰減，并記錄在該處水體吸收矩陣中。剩下的光子權重代入到散射后移動方向傳輸步長計算中。若光子權重低于一定小的閾值，則執(zhí)行輪盤賭算法來決定忽略此光子或繼續(xù)計算它的移動。

2.1 光子的初始化

每一個光子在最初統一設定一個權重W。當光子在水體邊界遇到折射率改變界面時，會發(fā)生鏡面反射。設入射空氣折射率為n1，水體折射率為n2，則鏡面反射率 Rsp為

則光子的權重被減去Rsp。

2.2 光子步長

根據吸收系數和散射系數的定義，光子與水體介質在單位步長［s1，s1+ds1］內相互作用（包括吸收與散射）的幾率為μ1ds1。由水體的比耳朗伯定律［4］可得:

其中，μa為吸收系數，μs為散射系數，μt是總衰減系數，單位是m-1。對上式進行變換，在［0，s1］內積分，得到指數分布:

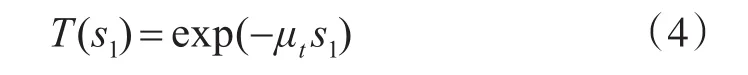
表示光子步長大于 s1的幾率，即P｛s≥s1｝。對于自由路徑s的累積分布:

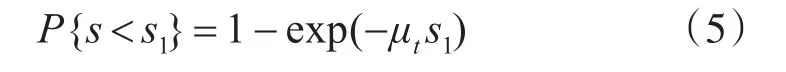
變換上式求解得到:

設定ζ=P｛s＜s1｝，且在（0，1］區(qū)間均勻分布，因此ζ與1-ζ的分布相同，則-ln（1-ζ）與-ln（ζ）等價，故:

依此式，在（0，1］區(qū)間內生成隨機數ζ，便得到步長s=s1。

2.3 光子移動

當s被確定以后，光子就可以在坐標系中移動。設光子的瞬時位置為（x，y，z），瞬時方向單位向量r，可表示為（μx，μy，μz）:

在移動后光子的位置為（x’，y’，z’），則:

2.4 邊界處理

在光子移動一個步長過程中，光子可能會遇到水體邊界。當光子遇到邊界時，光子可能反射（或透射）逃逸出水體或者向內部反射。光子向內反射的幾率取決于入射到邊界的角度（θi）。可計算得到:

由Snell公式表示入射角θi與折射角θt的關系。向內反射的幾率R（θi），可由Fresnel公式得出:

因此，1-R（θi）表示光子離開水體成為反射部分，計入反射矩陣。

在光子離開介質前，只行走了步長s的一部分。因此，實際離開位置應該是基于減短的步長s':

其中τ表示水體的厚度。若光子內反射，則光子權重計算為

剩下的光子有新的位置和方向。x，y坐標可直接用前述公式計算，z坐標更新為

2.5 光子吸收

當光子移動一定步長時，光子由于水體介質的吸收，會使得權重減小。權重減小的幅度ΔQ:

光子權重W更新:

由于（μa/μt+μs/μt）=1，因此能量是平衡的。

2.6 光子散射

當光子發(fā)生散射時，光子的軌道偏轉角度θ分布在［0，π］。Henyey與Greenstein［10］最早提出利用散射相函數來計算散射偏轉角的概率密度方程:

其中，g為各向異性因子，表示散射的角度分布。令μ=cosθ，分布在［-1，1］。可以推導出:

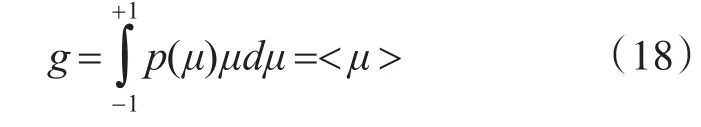
因此，g表示介質中散射角余弦的平均值。各向異性因子g取值在-1～1之間。

計算出偏轉角和方位角，新的光子軌道μ′x，）則可從舊的軌道（μx，μy，μz）和偏轉角θ與方位角ψ計算得到:

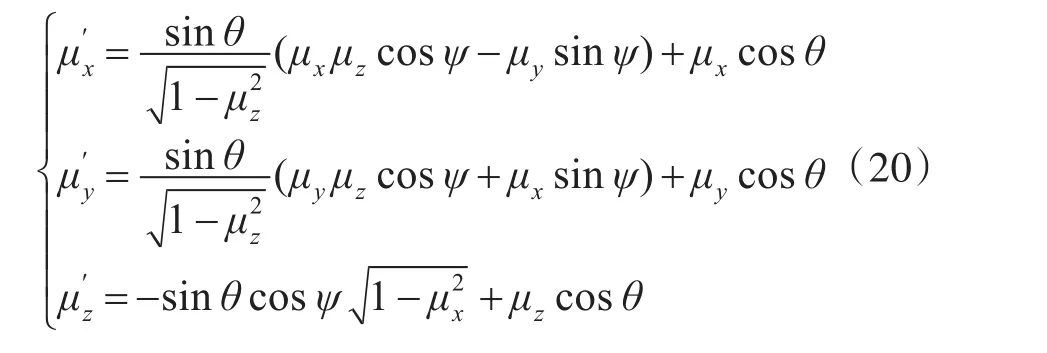
2.7 光子終止

若光子的權重衰減到足夠小，并低于一定閾值時，那么它的傳輸對計算結果的影響將可忽略。為了減小忽略權重而帶來的誤差。采用輪盤賭方法對權重小于閾值W的光子進行處理。在一定數量m的光子中讓其中一個光子能夠存活下來，并使權重增為mW，其他的光子則為0。

3 結果

3.1 水體參數設置

根據實際水體所滿足的參數和成像探測范圍，選取深度為30m，半徑為5m的圓柱形水體區(qū)域，網絡劃分的精度為0.01m，進行蒙特卡羅程序仿真實驗，如圖2所示。設從水體的吸收系數為0.2 m-1，散射系數為 0.1 m-1，各項異性因子為 0.8［11～12］。為了保證一定的仿真精度，選擇入射光子包數為100萬。

圖2 水體介質模型示意圖

3.2 單光子散射路徑

根據仿真設計的參數，首先分析單光子的散射路徑，并對單光子的散射路徑和散射方向進行描述，如圖3所示。部分單光子經過了水體的折射、散射和吸收后，最終又在水面出射（如圖3中上面三圖所示）；部分單光子經過水體折射、散射和吸收后，最終被吸收掉（如圖3中左下圖所示）；部分單光子進入水體后，直接在通過水體出射（如圖3中右下圖所示）。

3.3 水下光子密度空間分布

將100萬個光子在規(guī)定的水域中心位置，準直入射到水體中，光子經過水體的反射、折射、散射和吸收，并對100萬個光子能量進行統計，可以得到不同位置的光子密度空間分布和不同位置的光子密度空間分布等高線圖，如圖4所示。Colorbar采用jet顏色映射［13］，表示以10為底的光子數對數大小。

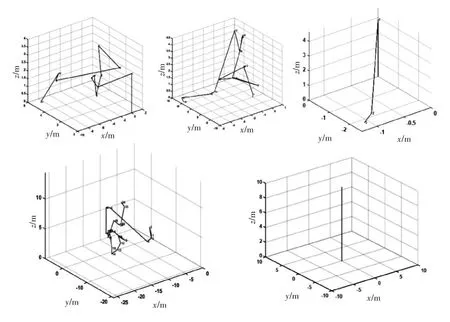
圖3 單個光子在水體中的散射路徑

圖4 光子密度空間分布仿真圖和高線圖

3.4 不同深度下徑向光子密度分布

根據仿真數據，進一步對比統計分析了在水下不同深度時，光子密度（或光子數）的徑向分布，如下圖所示。分別統計了水下深度為5m、15m和25m處的光子密度，其對數分布曲線如圖所示，可以看到光子密度隨著深度增加，光子密度整體上成遞減趨勢，但是在距離入射位置處光子密度比遠離入射位置處的值要大。在深度為25m時，光子密度已經非常低，達到10-4。

3.5 不同深度下散射光子分析

透過水體的光子可以分為彈道光子和散射光子，散射光子可以分為蛇形光子和擴散光子。一般地，認為彈道光子在傳統透鏡式成像中起到了主要貢獻，而散射光子是被水中散射子散射的光子，對成像起到干擾作用，為噪聲成分。

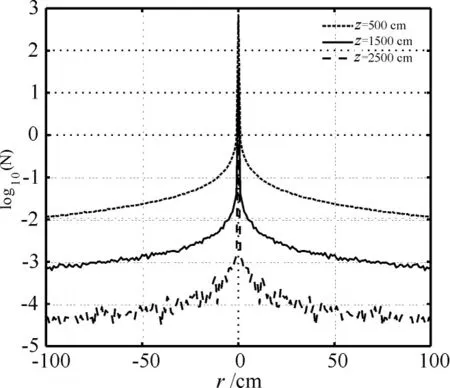
圖5 不同深度下光子數徑向分布

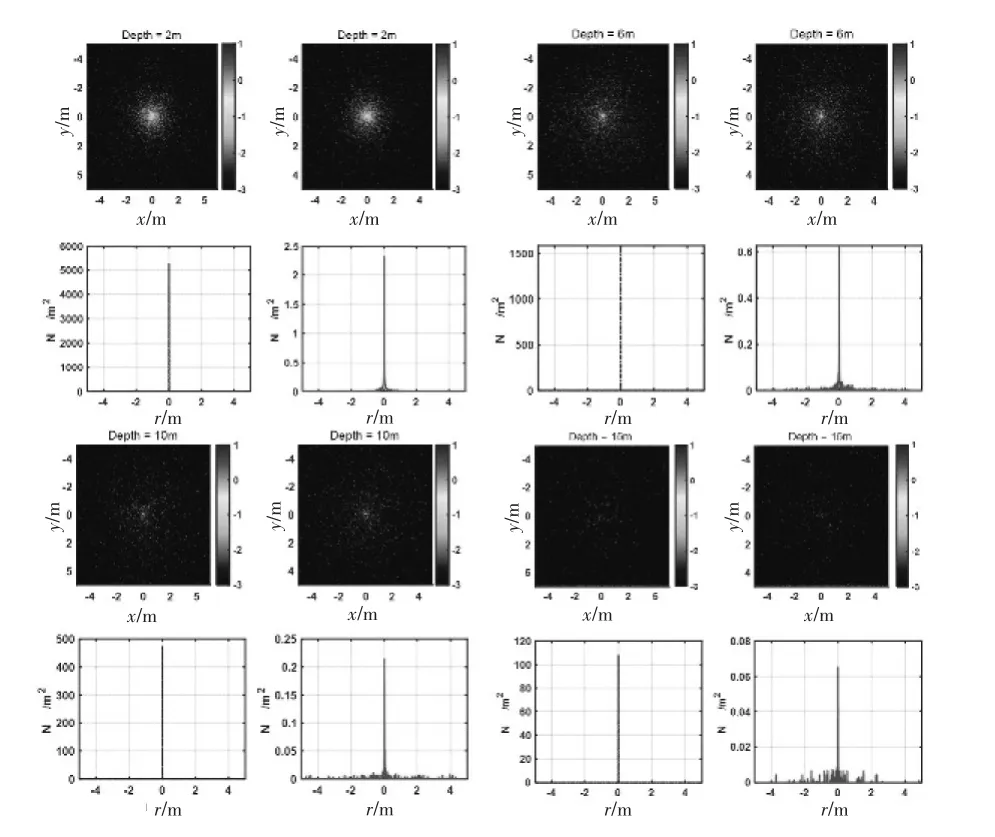
圖6 不同深度下，彈道光子去除和未去除透射光照度對比

為了對比分析不同水體深度下，彈道光子去除和未去除時對透射光子密度分布影響，分別對水深度為2m、6m、10m和15m的水體仿真研究，其對比圖如圖6所示。在每個水體深度下，左上圖是未去除彈道光子的透射光子密度分布圖像，左下圖是未去除彈道光子的透射光子密度分布圖像對應y為0位置的光子密度分布（Colorbar以光子密度的對數形式表示出），右上圖是去除彈道光子的透射光子密度分布圖像，右下圖是去除彈道光子的透射光子密度分布圖像對應y為0位置的光子密度分布。其他水體深度，同理可得到如圖4所示。

由圖中可以看出，未去除彈道光子時x為0位置處的光子密度數遠大于去除彈道光子時，但是隨著深度增加，其比值會逐漸減小，說明散射光子在深度比較小時對成像影響比較小，但是在水體深度比較大時，彈道光子較少，散射光子也會減小，值得注意的是，彈道光子減小的比例比散射光子減小的比例要大。所以在大深度區(qū)域成像時，主要貢獻的直行光子會被噪聲淹沒，無法進行成像。

4 結語

本文基于蒙特卡羅仿真思想設計了水下光場傳輸的蒙特卡羅程序算法，選取實際水體參數，對水下單光子散射路徑、水體光子密度分布、不同深度徑向光子密度分布和不同深度下散射光子影響進行了仿真分析。單光子路徑主要有三種情況:直接透射、最終出射水面、最終吸收。光子包垂直進入水中時，彈道光子密度數遠大于散射光子時，但是隨著深度增加，其比值會逐漸減小，說明散射光子在深度比較小時對成像影響比較小，但是在水體深度比較大時，彈道光子減小的比例比散射光子減小的比例要大。所以在大深度區(qū)域成像時，起主要貢獻的直行光子會被噪聲淹沒，無法進行成像。