GPS/BDS/Galileo三頻精密單點定位模型及性能分析

周 鋒，徐天河

1. 山東科技大學測繪科學與工程學院，山東 青島 266590； 2. 山東大學空間科學研究院，山東 威海 264209

精密單點定位(precise point positioning，PPP)是指利用外部提供的高精度衛星軌道和鐘差產品，在綜合考慮各項誤差精確改正的基礎上，采用合理的參數估計策略(如最小二乘或Kalman濾波等)，利用單臺GNSS接收機的載波相位和偽距觀測值實現全球高精度絕對定位(一般可達分米至毫米級)的一項技術[1]。PPP技術自20世紀90年代被提出并實現后[2-3]，經過將近30年的快速發展，基本理論和工程實踐已日趨成熟，目前已廣泛應用于廣域精密定位、低軌衛星定軌、水汽反演與電離層監測、地震與海嘯的監測和預警、時間傳遞等領域[4-7]。

得益于全球分布的大地型GNSS接收機，PPP技術自問世以來，大多采用雙頻PPP模型，已有學者從模糊度固定角度詳細論述了不同雙頻PPP模型的相互關系[8]。隨著美國GPS現代化、我國BDS和歐盟Galileo導航衛星系統的迅速建設，越來越多的導航衛星開始播發三頻信號，三頻PPP的研究和應用也越來越廣泛與深入[9]。基于BDS三頻觀測值，文獻[10—11]系統研究了3種BDS三頻PPP觀測模型及其定位性能，即基于B1/B2和B1/B3無電離層組合觀測值、基于單個無電離層組合觀測值及基于非差非組合觀測值的三頻PPP模型。文獻[12]基于GPS三頻觀測值對比分析了不同三頻PPP模型的定位性能。不同研究結果表明，三頻PPP與雙頻PPP在收斂性能和定位精度等性能指標上基本相當。針對城市復雜環境下(如信號遮擋、衰減和多徑頻繁發生)的智能交通、自動駕駛等對高精度動態定位的需求，文獻[13]充分利用三頻多系統GNSS數據，提出單歷元寬巷模糊度固定PPP方法，并與傳統雙頻PPP和廣域偽距增強精密定位方法進行對比分析。結果表明，在干擾因素多的城市復雜環境中，單歷元寬巷模糊度固定PPP定位效果更好。可以看出，三頻觀測值的加入，不僅可以提升PPP模糊度固定效率，還將提升復雜場景下PPP定位的可用性及可靠性。

近年來，已有大量研究針對三頻PPP模型與定位性能進行了廣泛的驗證與分析，但鮮有文獻對三頻PPP模型間進行系統性的研究與比較，而且對三頻PPP模型中GNSS偏差的產生機制及數學表達缺乏深入探討。從原始非差非組合觀測方程出發，在精細考慮偽距和載波相位硬件偏差的基礎上，本文詳細地研究了3種常用的三頻PPP函數模型的獨立參數化方法，系統分析了3種PPP模型的相互關系，并給出了非組合模式下兩類GNSS偏差(如接收機偽距頻間偏差和載波相位頻間衛星鐘偏差)嚴格的數學表達形式。本文利用GPS/BDS/Galileo三頻PPP算例，分析驗證了理論的正確性及不同模型的定位性能。

1 三頻PPP觀測模型

本節給出三頻PPP的觀測模型，包括函數模型及其對應的隨機模型。為簡單起見，利用L1、L2和L3分別表示GPS L1、L2和L5頻率，BDS B1、B2和B3頻率及Galileo E1、E5a和E5b頻率。具體見表1。

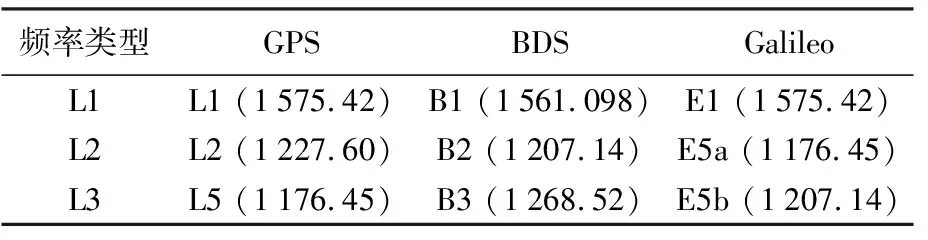
表1 GPS/BDS/Galileo衛星系統及其對應的頻率

1.1 函數模型

從非差非組合GNSS原始觀測方程出發，建立三頻PPP函數模型，并對不同模型的異同點進行了細致研究。

1.1.1 原始觀測方程

一般地，非差非組合GNSS偽距和載波相位觀測方程可表示如下

(1)

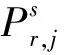
對于偽距和相位硬件偏差，通常認為偽距硬件偏差比較穩定，一天內變化較小[15-16]。而相位硬件偏差具有明顯的時變特性，可將相位硬件偏差分解為常數部分和時變部分[17-18]，即

(2)

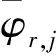
為簡便起見，定義以下變量

(3)

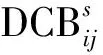
目前GNSS精密衛星鐘差產品一般是基于L1/L2雙頻(如GPS L1/L2、BDS B1/B2與Galileo E1/E5a)無電離層組合偽距和載波觀測值計算得到[19]。因此，精密衛星鐘差包含了雙頻偽距硬件偏差與相位硬件偏差時變部分的線性組合，即

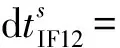
(4)

引入精密衛星軌道和鐘差改正，將式(4)代入式(1)并線性化得

(5)

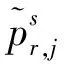
(6)

顧及式(6)，則式(5)可進一步寫為

(7)

式中

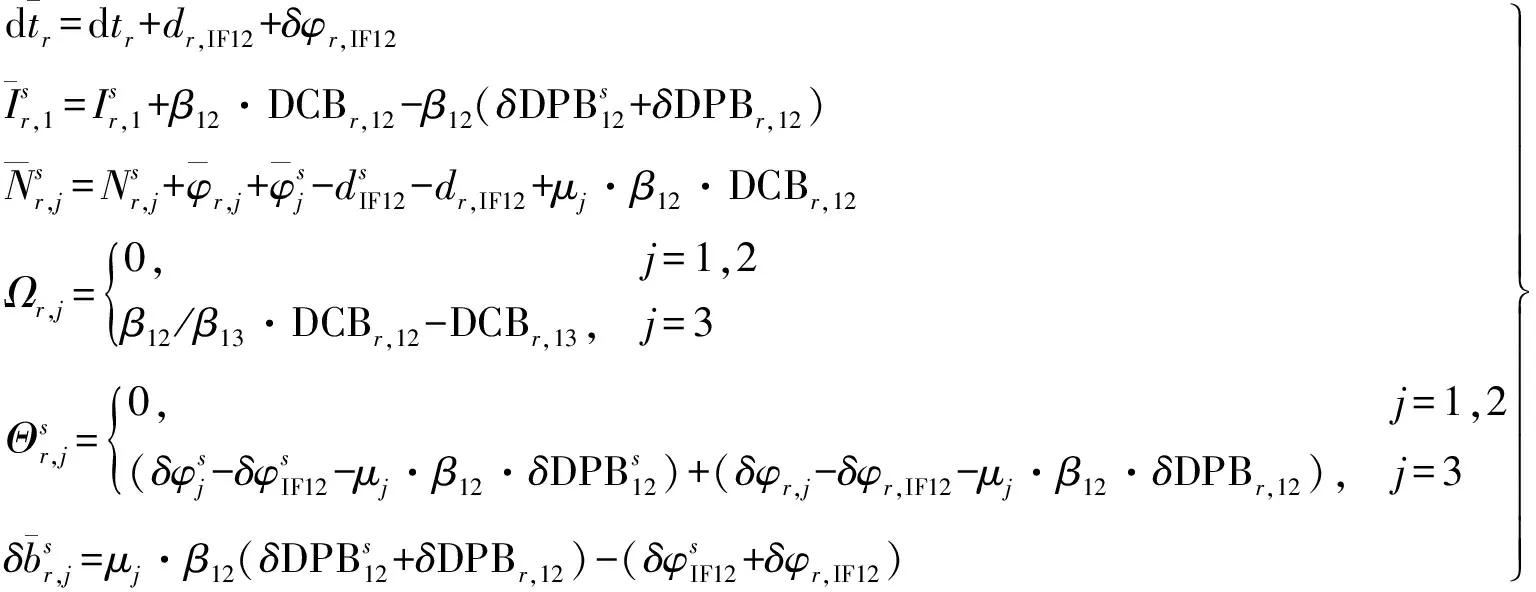
(8)

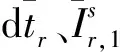
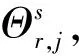
IFCB估計一般基于經典的無幾何距離無電離層(geometry-free and ionospheric-free，GFIF)組合觀測量計算得到[17,20]。文獻[21—22]論證了IFCB與衛星有關，而與接收機無關，并給出了將GFIF組合觀測量估計的IFCB轉化為非組合觀測值下的IFCB的轉換關系，即

(9)

接著，在式(7)的基礎上，建立3種常用的三頻PPP函數模型。為簡便起見，用IF1213-PPP、IF123-PPP和UC123-PPP分別表示基于L1/L2和L1/L3兩個無電離層組合觀測值、基于單個無電離層組合觀測值及基于非差非組合觀測值的三頻PPP模型。首先給出三頻偽距和載波相位OMC觀測向量，即

(10)

1.1.2IF1213-PPP模型

IF1213-PPP由兩個不同的無電離層組合觀測量得到，可表達為

(11)

為使觀測方程中接收機鐘差參數保持一致，將式(11)展開并改寫為

(12)

式中

(13)

式中，Ωr,IF1213為IF1213組合下的接收機IFB。

可以得出，IF1213-PPP的待估參數向量為

(14)

1.1.3IF123-PPP模型

IF123-PPP利用三頻觀測值直接組成無電離層組合觀測量，即

(15)

式中，設計矩陣AIF123=[e1e2e3]，e1、e2和e3為線性組合系數，且滿足以下關系式

(16)

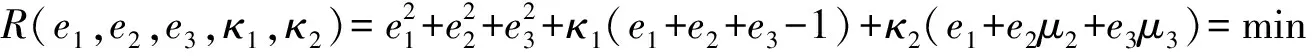
(17)

將式(15)展開，得

(18)

式中

(19)

相應地，IF123-PPP的待估參數向量為

X=[xdtr,IF123ZrNr,IF123]

(20)

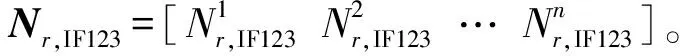
1.1.4UC123-PPP模型

UC123-PPP在不同頻率觀測值之間不作線性組合，而是直接利用原始偽距和載波觀測值，即

(21)

式中，設計矩陣AUC123=diag(1,1,1)。其中，diag(·)表示對角陣。

結合式(7)和式(8)，將式(21)進一步展開為

(22)

相應地，UC123-PPP的待估參數向量為

(23)

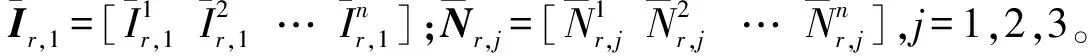
1.1.5 三頻PPP模型間的聯系

在觀測方程層面，IF1213-PPP、IF123-PPP和UC123-PPP都是基于三頻原始觀測值的線性組合形成，設計矩陣(或線性組合系數陣)分別對應AIF1213、AIF123和AUC123。不同的是，前兩者需對不同頻率觀測值進行線性組合以消除電離層延遲影響，而UC123-PPP在不同頻率觀測值之間無須做線性組合。

在待估參數層面，3個模型對應相同的位置參數和對流層濕延遲參數，而估計的載波相位模糊度各不相同；不同于IF123-PPP，IF1213-PPP和UC123-PPP估計相同的接收機鐘差參數。此外，IF1213-PPP和UC123-PPP需分別估計一個接收機偽距IFB參數，且兩者存在下述轉換關系

Ωr,IF1213=β12DCBr,12-β13DCBr,13≡β13·Ωr,3

(24)

1.2 隨機模型

假設不同頻率觀測值之間相互獨立，且不同頻率偽距或載波相位觀測值噪聲相同，即滿足σP1=σP2=σP3=σP和σL1=σL2=σL3=σL。非組合三頻觀測值對應的方差-協方差陣ΣUC可以表示為

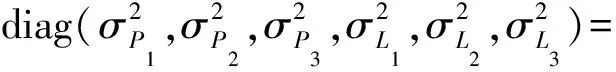
(25)

式中，σP|L=a/sin(E)，其中a為觀測值噪聲，對于載波觀測值，一般經驗地取為0.003 m；而對于偽距觀測值，一般取0.3 m；E為衛星高度角。

根據誤差傳播定律，IF1213-PPP、IF123-PPP和UC123-PPP對應的方差-協方差陣為

(26)

式中，ΣIF1213、ΣIF123和ΣUC123分別為IF1213-PPP、IF123-PPP和UC123-PPP模型的觀測值方差-協方差陣。

2 試驗結果分析

2.1 數據介紹及處理策略

為驗證GPS/BDS/Galileo三頻PPP定位性能，選取均勻分布的25個MGEX測站于2019年7月的觀測數據(采樣間隔為30 s)進行數據處理，測站地理分布見圖1，測站所處經緯度、配備的接收機類型和天線類型信息見表2。可以看出，所選測站的接收機類型有4種，分別是SEPT POLARX5、JAVAD TRE_3 DELTA、TRIMBLE ALLOY和TRIMBLE NETR9，其中配備TRIMBLE NETR9和SEPT POLARX5接收機的測站占比分別為56%和32%。此外，所選測站均具備跟蹤GPS/BDS/Galileo三頻信號的能力且滿足每個歷元跟蹤到每個衛星系統的衛星數均大于或等于4顆。表3給出了可以播發三頻觀測值的GPS、BDS和Galileo衛星情況，其中包括部分GPS衛星(12顆)以及全部的BDS(15顆)和Galileo衛星(24顆)。

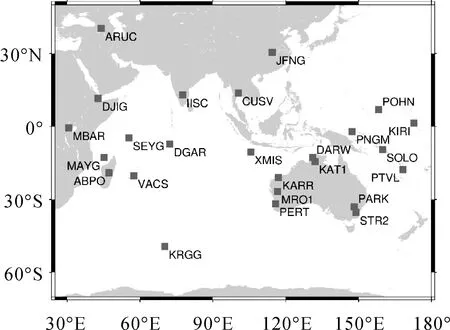
圖1 選取的25個MGEX測站分布Fig.1 Geographical distribution of the selected 25 MGEX tracking stations

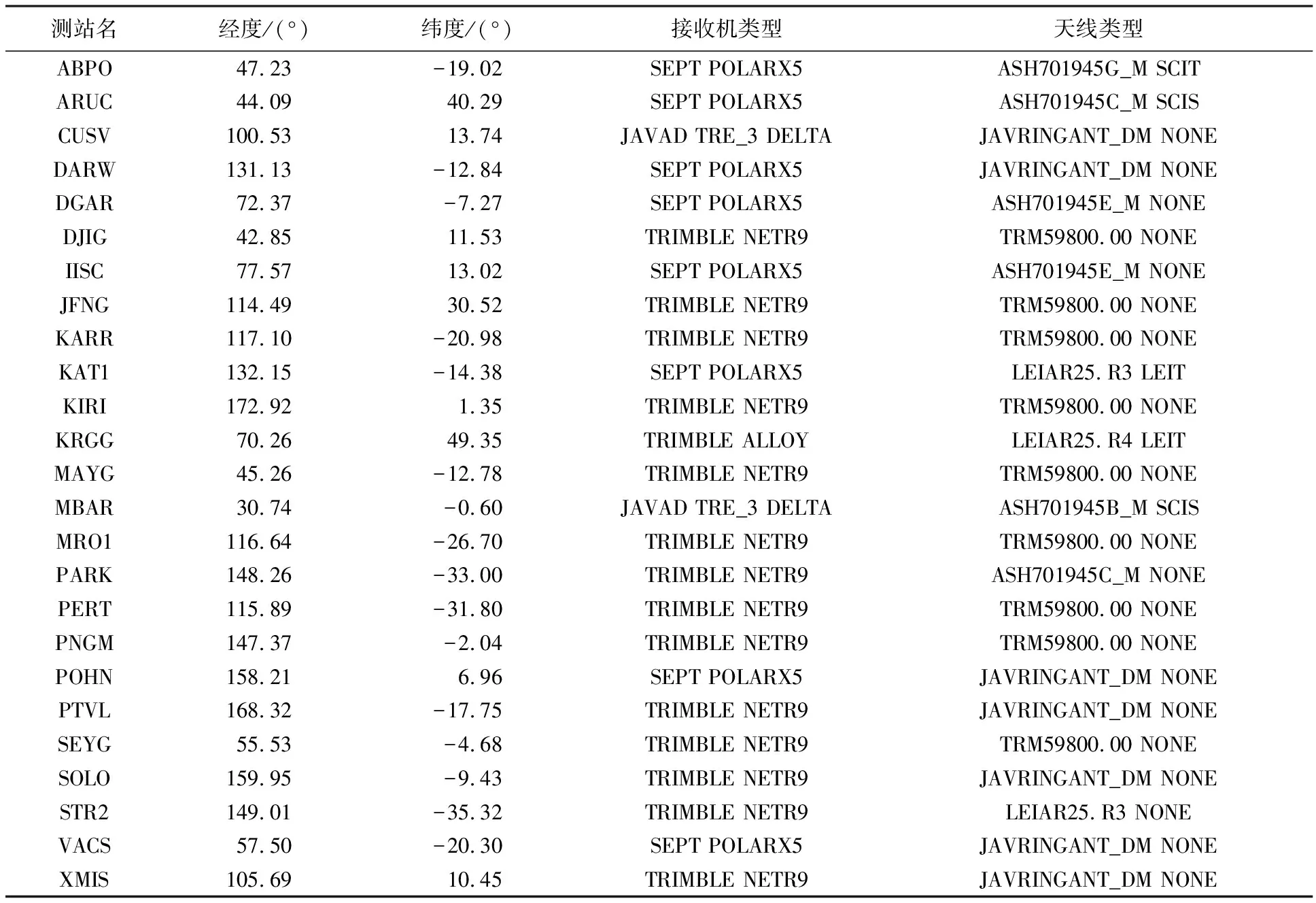
表2 所選MGEX測站基本信息

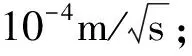
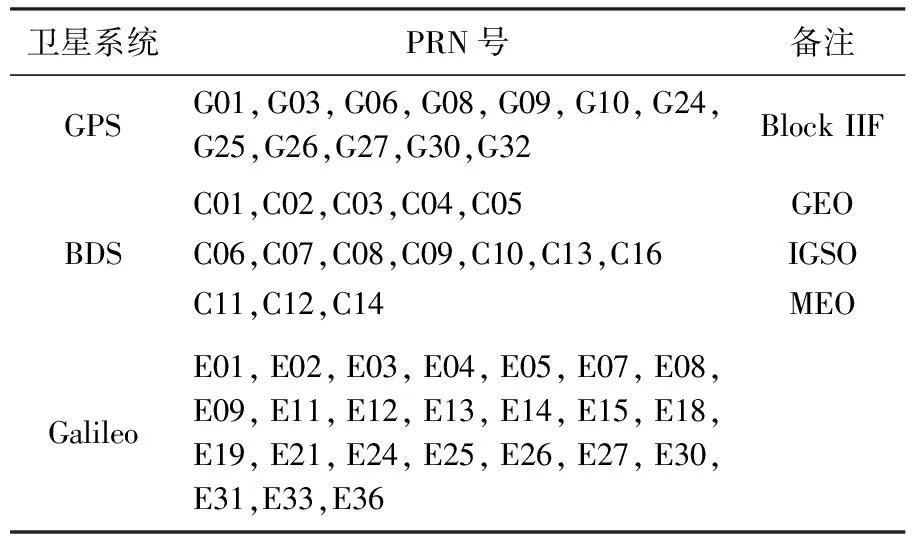
表3 具備三頻信號播發能力的GPS/BDS/Galileo衛星情況

當坐標的東(E)、北(N)、垂向(U)3個方向定位偏差均小于1 dm時，認為濾波收斂，選取濾波解穩定后(本文選定濾波開始2 h后)的定位偏差用于統計定位精度[25]。利用箱線圖來描述定位精度的分布情況，其中上、下邊緣線分別表示95%和5%分位數，矩形盒的上、下兩端線分別表示75%和25%分位數，矩形盒內部線表示中位數，即50%分位數[26]。

2.2 靜態PPP

算例給出5種GPS/BDS/Galileo靜態PPP模型定位情況，選取了雙頻無電離層組合模型IF12-PPP與雙頻非組合模型UC12-PPP作為對比。圖2為測站KAT1和KIRI在年積日(day of year，DOY)182的靜態定位誤差曲線圖。可以看出，在收斂階段IF123-PPP表現相對其他模型稍差一些，這主要是由于具有三頻觀測值的GPS衛星較少(僅有12顆)，而IF123-PPP模型對三頻觀測值完整性的要求更為苛刻，導致其參與數據解算的GPS觀測值數量相比其他模型下降明顯。以KAT1測站為例，IF123-PPP、IF1213-PPP和UC123-PPP解算用到的GPS平均衛星數分別為4.2、10.4和10.4。待濾波解充分收斂后，5種PPP模型定位誤差曲線基本重合。

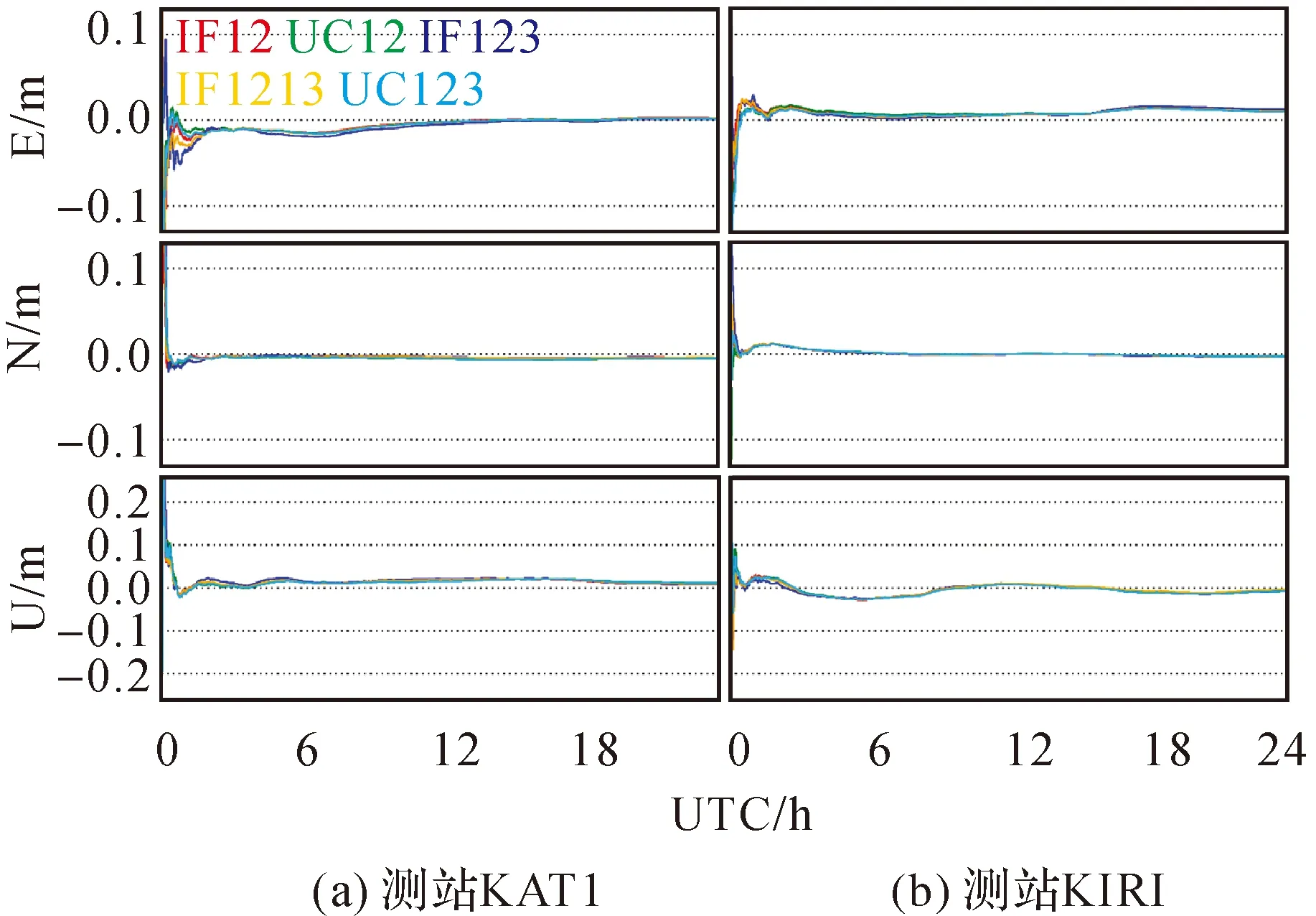
圖2 5種模型GPS/BDS/Galileo靜態PPP定位誤差(年積日182，2019)Fig.2 Positioning errors derived from five GPS/BDS/Galileo static PPP solutions on DOY 182, 2019

圖3給出了所選25個測站一個月不同PPP模型靜態定位模式下定位精度分布箱線圖，表4列出了其定位精度的中位數統計。從圖中可以看出，相比雙頻PPP，三頻觀測值的加入對GPS/BDS/Galileo PPP定位精度提升不明顯，三頻PPP定位性能與雙頻PPP基本相當。從表4可得，5種靜態PPP模型收斂后的水平方向精度優于1.0 cm，高程方向優于1.5 cm。

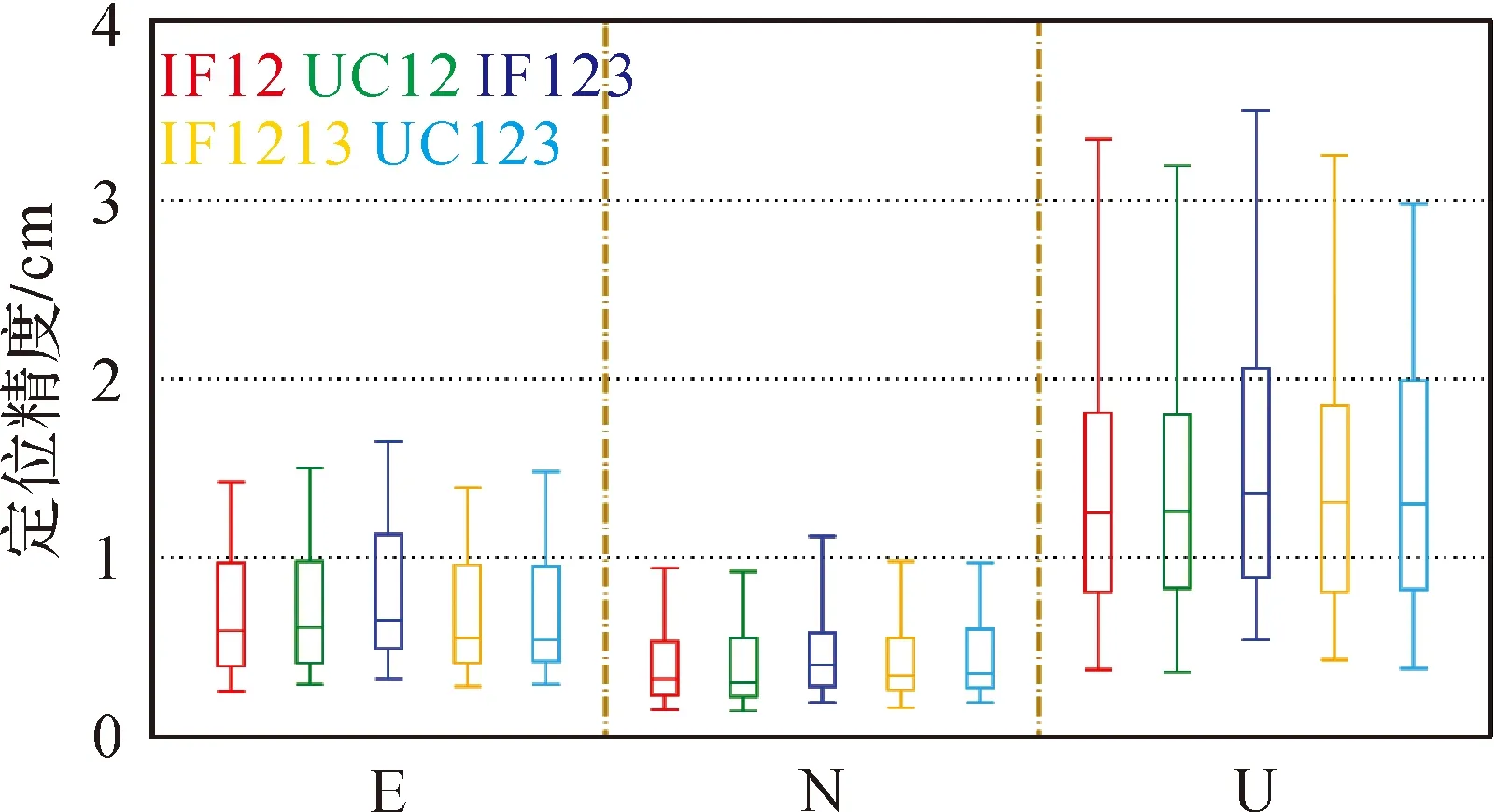
圖3 5種模型GPS/BDS/Galileo靜態PPP定位精度分布Fig.3 Distribution of positioning accuracy among five GPS/BDS/Galileo PPP models in static mode

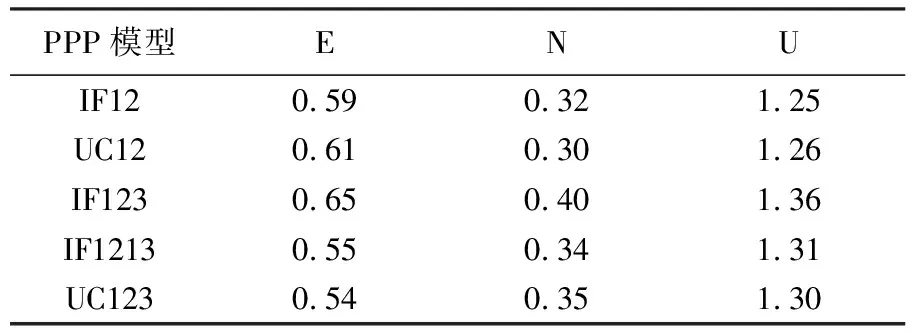
表4 5種模型GPS/BDS/Galileo靜態PPP靜態定位精度統計

由式(24)可以得出，IF1213-PPP和UC123-PPP估計的接收機IFB的轉換系數為β13，對應GPS為-1.261、BDS為-1.944、Galileo為-1.422。圖4給出了DOY 182不同測站IF1213-PPP和UC123-PPP估計的接收機IFB間轉換系數。從估計的IFB得到的轉換系數與參考值的吻合程度來看，Galileo最好，BDS次之，而GPS最差，這是因為GPS三頻觀測值衛星為MEO衛星，每個測站實際觀測到的三頻GPS衛星相對BDS和Galileo要少。仍以DOY 182 KAT1測站為例，可觀測到的具有三頻觀測值的GPS、BDS和Galileo平均衛星數分別為4.2、10.7和7.3，其中BDS大部分為GEO和IGSO衛星。此外，接收機IFB與偽距觀測值有關，相比GPS和BDS，Galileo的偽距觀測值質量更好[27]。

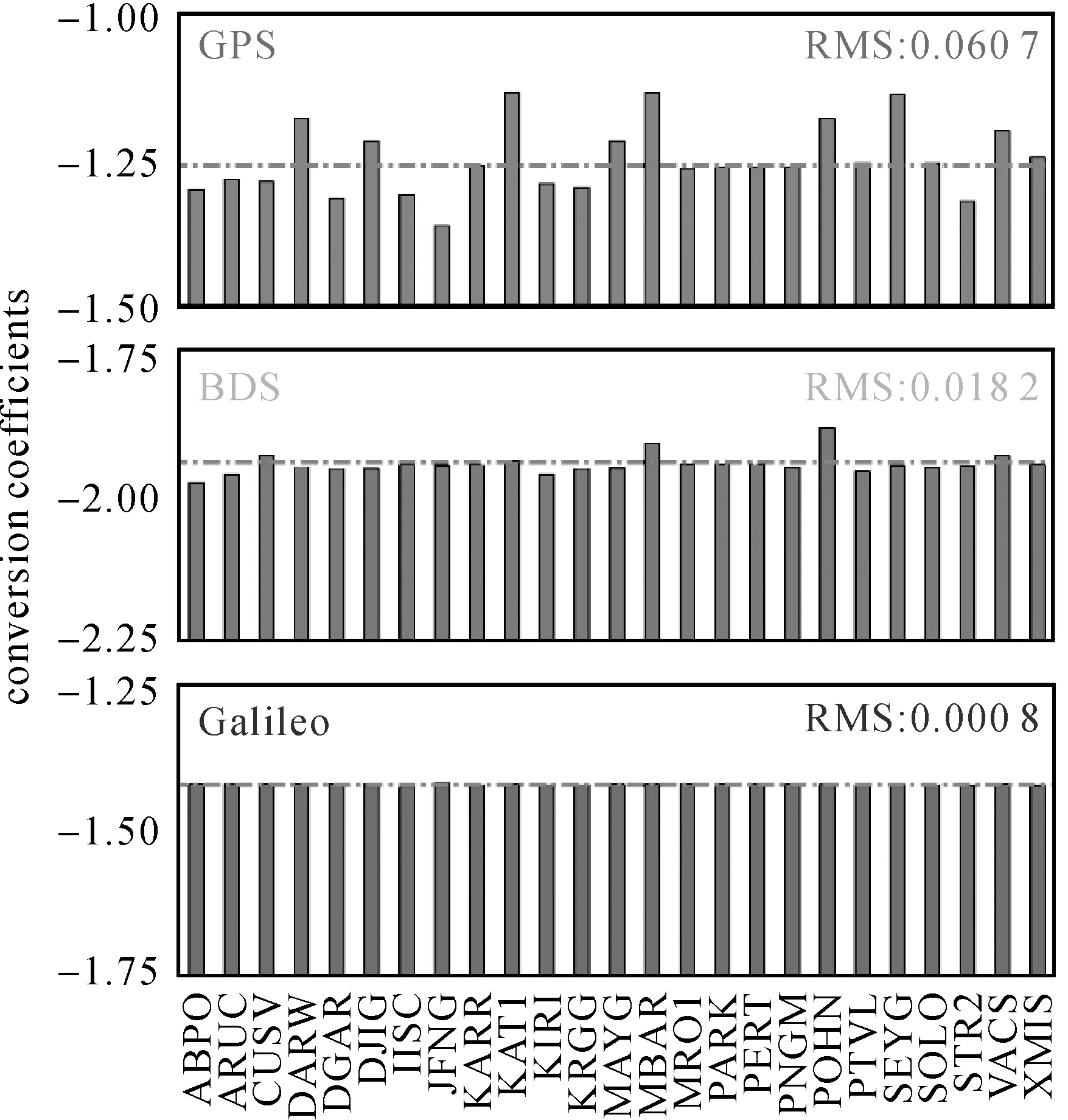
圖4 不同測站IF1213-PPP和UC123-PPP估計的接收機IFB間轉換系數(DOY 182，2019)Fig.4 Conversion coefficients of receiver IFBs derived from IF1213-PPP and UC123-PPP for different stations (DOY 182，2019)

2.3 動態PPP

算例給出5種GPS/BDS/Galileo動態PPP模型定位情況。圖5為測站KAT1和KIRI在DOY 182的動態定位誤差曲線圖。與靜態PPP相比，IF123-PPP動態定位誤差與其他PPP模型差異較明顯，可見動態PPP對可觀測衛星數的變化更敏感。因此，對于三頻PPP定位，若有GPS觀測值加入時，不建議采用IF123-PPP模型。整體來看，除了IF123-PPP，其他4種PPP模型定位誤差吻合較好。從圖6和表5可以看出，三頻IF1213-PPP、UC123-PPP與雙頻IF12-PPP、UC12-PPP的定位精度基本相當，而IF123-PPP定位精度稍差，整體上，5種動態PPP模型收斂后的水平精度優于2.0 cm，高程精度優于5.0 cm。

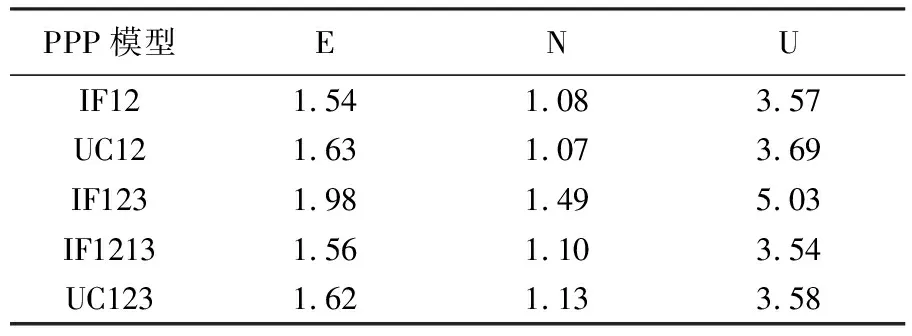
表5 不同GPS/BDS/Galileo PPP模型動態定位精度

此外，為了測試不同PPP模型的解算效率，圖7表示DOY 182不同測站不同PPP模型的解算時間(計算機為八核Intel Core i7-8550U處理器，CPU主頻1.8 GHz)。很明顯，基于非組合觀測值的PPP模型具有更多的觀測值與待估參數，因此其計算時間明顯大于無電離層組合PPP模型。

3 結 論

本文對三頻PPP模型中出現的偏差項(如接收機IFB、載波相位IFCB等)進行了較為詳細的分析和描述。在充分考慮偽距和載波相位硬件延遲的基礎上，從公式推導的角度，詳細討論了3種三頻PPP模型的獨立參數化方法，并從觀測方程和參數估計角度，論述了不同三頻PPP模型的相互關系。試驗分析了3種PPP模型的靜態、動態定位精度，得出以下結論。

(1) 由于當前GPS衛星僅有12顆可播發三頻信號，因此有GPS觀測值參與的三頻PPP解算，不建議采用IF123-PPP模型。

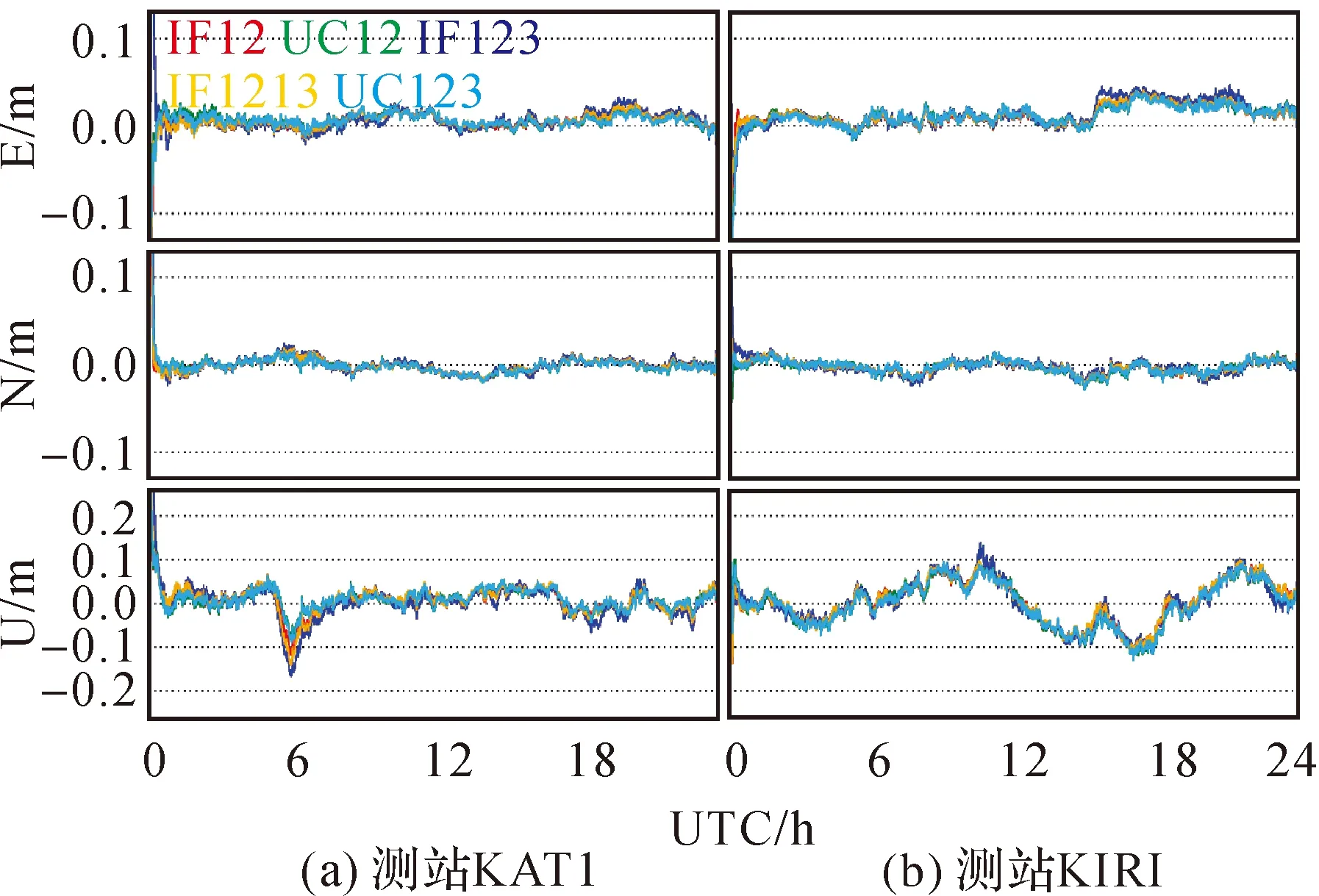
圖5 5種模型GPS/BDS/Galileo動態PPP定位誤差(年積日182，2019)Fig.5 Positioning errors derived from five GPS/BDS/Galileo kinematic PPP solutions on DOY 182, 2019

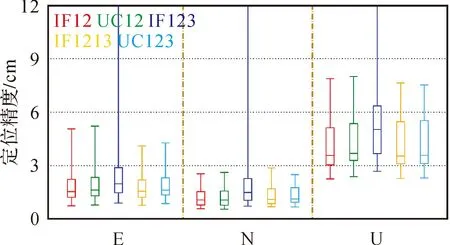
圖6 5種模型GPS/BDS/Galileo動態PPP定位精度分布圖Fig.6 Distribution of positioning accuracy among five GPS/BDS/Galileo PPP models in kinematic mode

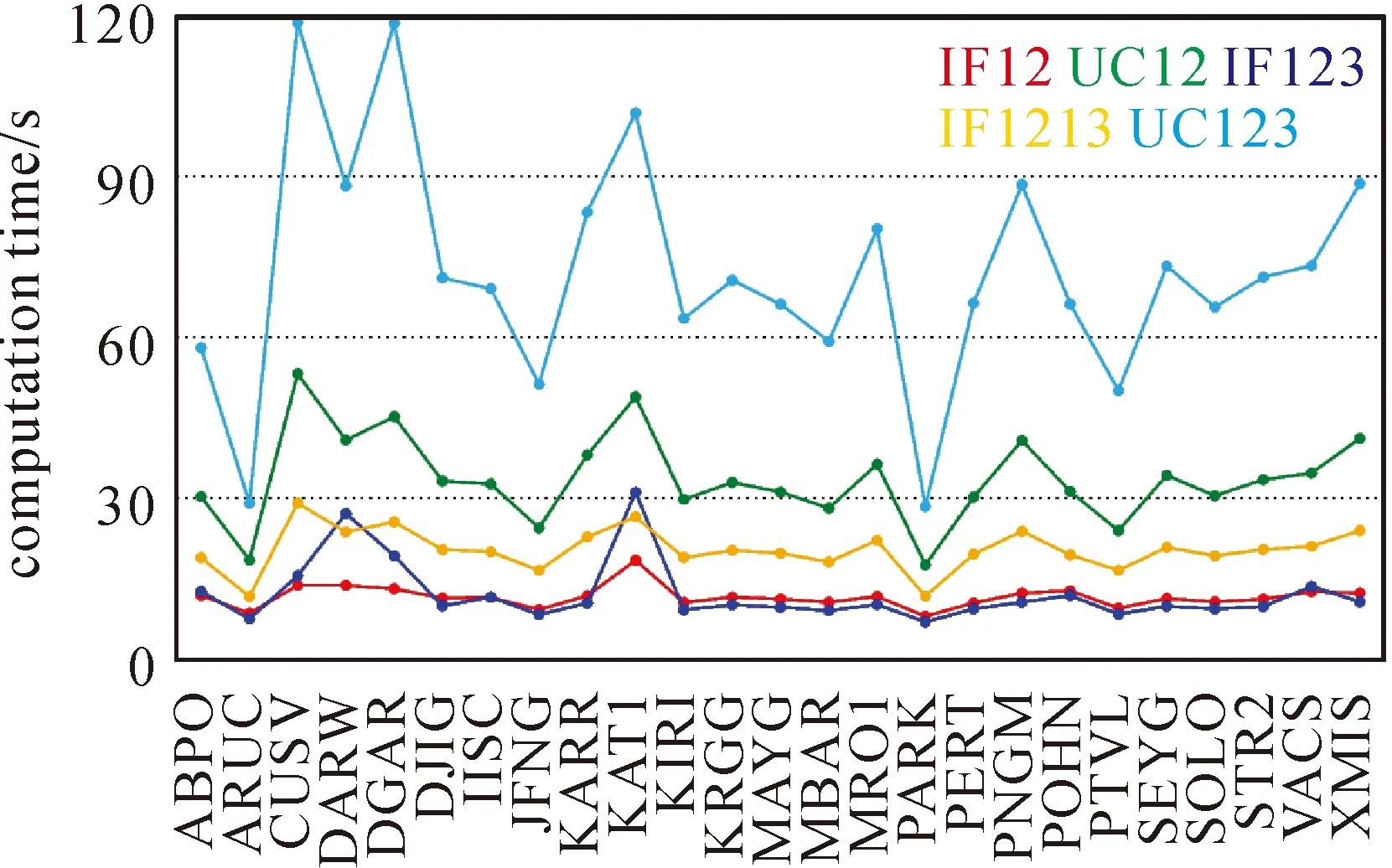
圖7 不同PPP模型數據解算耗時對比(DOY 182，2019)Fig.7 Computation time for different PPP processing (DOY 182，2019)

(2) 不考慮IF123-PPP模型，待濾波收斂后，雙頻、三頻非組合PPP與相應的無電離層組合PPP定位精度基本相當。相比雙頻PPP，三頻觀測值的加入對PPP定位性能的提升不明顯，三頻PPP與雙頻PPP的定位精度基本相當。

(3) GPS/BDS/Galileo三頻PPP，在靜態定位模式下，收斂后水平方向精度優于1.0 cm，高程方向優于1.5 cm；而在動態定位模式下，收斂后水平精度優于2.0 cm，高程方向優于5.0 cm。