半結(jié)合3-代數(shù)的雙模結(jié)構

白瑞蒲, 劉 山, 張 艷

(河北大學 數(shù)學與信息科學學院, 河北 保定 071002)

1 引言與預備知識

文獻[1]定義了半結(jié)合3-代數(shù), 并研究了其基本結(jié)構. 半結(jié)合3-代數(shù)(A,{,,})是具有三元線性運算{,,}:A?A?A→A的線性空間, 且滿足?xi∈A, 1≤i≤5, 有

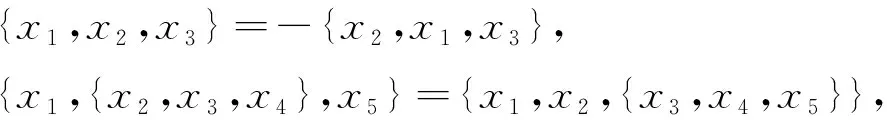
(1)

{x1,{x2,x3,x4},x5}={x5,{x2,x3,x4},x1}+{x1,{x5,x3,x4},x2}.

(2)

因三元代數(shù)在數(shù)學及數(shù)學物理中應用廣泛, 因此對其結(jié)構的研究備受關注[2-5]. 一般研究從熟知的代數(shù)結(jié)構中構造具有應用性質(zhì)的三元代數(shù), 或構造與3-李代數(shù)、 3-Pre-李代數(shù)及局部上循環(huán)3-李代數(shù)等有密切關系的三元代數(shù)[6-7]. 研究表明, 每個半結(jié)合3-代數(shù)都有其伴隨3-李代數(shù). 3-李代數(shù)(L,[,,])[8-9]是具有線性運算[,,]:L∧L∧L→L的線性空間L, 且滿足?xi∈L, 1≤i≤5, 有

[[x1,x2,x3],x4,x5]=[[x1,x4,x5],x2,x3]+[x1,[x2,x4,x5],x3]+[x1,x2,[x3,x4,x5]].

(3)

2 半結(jié)合3-代數(shù)的伴隨3-李代數(shù)

[x1,x2,x3]={x1,x2,x3}+{x2,x3,x1}+{x3,x1,x2}, ?x1,x2,x3∈A.

(4)

進一步, 如果I是半結(jié)合3-代數(shù)A的理想(子代數(shù)), 則I是伴隨3-李代數(shù)Ac的理想(子代數(shù)).

證明: 由式(1),(2)可知, 乘法[,,]是完全交錯的, 且?xi∈A, 1≤i≤5, 有

所以式(3)成立, 從而(A,[,,])是3-李代數(shù). 進一步, 如果I是半結(jié)合3-代數(shù)A的理想(子代數(shù)), 則直接計算可得結(jié)果. 證畢.

3-李代數(shù)(A,[,,])稱為半結(jié)合3-代數(shù)A的伴隨3-李代數(shù), 簡記為Ac. 下面討論半結(jié)合3-李代數(shù)A的導子與伴隨3-李代數(shù)的導子之間的關系.

設A是半結(jié)合3-代數(shù),D:A→A是線性映射. 如果D滿足

D{x1,x2,x3}={Dx1,x2,x3}+{x1,Dx2,x3}+{x1,x2,Dx3}, ?x1,x2,x3∈A,

則稱D是A的導子[1]. 記Der (A)是A的導子全體, Der(Ac)是伴隨3-李代數(shù)Ac的導子代數(shù). 直接計算可知Der(A)是一般線性李代數(shù)gl(A)的子代數(shù).

對x1,x2∈A, 定義線性映射L(x1,x2),R(x1,x2):A×A→A,

L(x1,x2)(x)={x1,x2,x},R(x1,x2)(x)={x,x1,x2}, ?x∈A,

L(x1,x2)和R(x1,x2)分別稱為由x1,x2確定的左乘映射和右乘映射. 記

L(A)=〈L(x1,x2)|?x1,x2∈A〉,

R(A)=〈R(x,x2)|?x1,x2∈A〉.

由文獻[1]可知,

L(x1,x2)?Der(A),R(x1,x2)?Der(A).

定理2設A是半結(jié)合3-代數(shù), 則半結(jié)合3-代數(shù)A的導子代數(shù)Der(A)是Der(Ac)的子代數(shù), 且L(A),R(A)?Der(Ac).

證明: 對任意D∈Der(A)及x,y,z∈A, 由式(4)有

D[x,y,z]=D({x,y,z}+{y,z,x}+{z,x,y})=[Dx,y,z]+[x,Dy,z]+[x,y,Dz],

所以D∈Der(Ac), 且Der(A)是Der(Ac)的子代數(shù). 由式(1)～(4), ?x,y,u,v,w∈A, 有

L(x,y)[u,v,w]=[L(x,y)(u),v,w]+[u,L(x,y)(v),w]+[u,v,L(x,y)(w)],

從而L(x,y)∈Der(Ac), 同理?x,y∈A,R(x,y)∈Der(Ac). 證畢.

3 半結(jié)合3-代數(shù)的雙模

設L是3-李代數(shù),V是線性空間, 如果線性映射ρ:L∧L→gl(V)滿足: ?x1,x2,x3,x4∈L, 有

[ρ(x1,x2),ρ(x3,x4)]=ρ([x1,x2,x3],x4)+ρ(x3,[x1,x2,x4]),

(5)

ρ([x1,x2,x3],x4)=ρ(x1,x2)ρ(x3,x4)+ρ(x2,x3)ρ(x1,x4)+ρ(x3,x1)ρ(x2,x4),

(6)

則稱(V,ρ)是3-李代數(shù)L-模.

設A是半結(jié)合3-代數(shù),V是線性空間, 如果雙線性映射l,r:A×A→End(V)滿足: ?x1,x2,x3,x4∈A, 有

(7)

r({x1,x2,x3},x4)=r(x1,{x2,x3,x4})=r(x1,x4)r(x2,x3),

(8)

r(x1,x2)r(x3,x4)=r(x2,x1)l(x3,x4)+r(x1,x3)l(x2,x4),

(9)

r({x1,x2,x3},x4)=l(x4,{x1,x2,x3})+r({x4,x2,x3},x1),

(10)

r(x1,x2)r(x3,x4)=r(x1,x2)l(x3,x4)=l(x1,x3)r(x4,x2)=-l(x1,{x3,x2,x4}),

(11)

則稱(l,r,V)是半結(jié)合3-代數(shù)A的雙模.

定理3設A是半結(jié)合3-代數(shù),l,r:A×A→End(V)是線性映射, 則(l,r,V)是A的雙模的充要條件是(AV,{,,}lr)是半結(jié)合3-代數(shù), 其中?xi∈A,vi∈V,i=1,2,3, 有

{x1+v1,x2+v2,x3+v3}lr={x1,x2,x3}+l(x1,x2)v3-r(x1,x3)v2+r(x2,x3)v1.

(12)

證明: 如果(l,r,V)是半結(jié)合3-代數(shù)A的雙模, 則由式(8)～(10),(12)知, 對?xi∈A,vi∈V, 1≤i≤5, 有

{x1+v1,x2+v2,x3+v3}lr=-{x2+v2,x1+v1,x3+v3}lr,

所以(AV,{,,}lr)是半結(jié)合3-代數(shù). 反之, 如果(AV,{,,}lr)是半結(jié)合3-代數(shù), 則由式(12)知, ?xi∈A,vi∈V, 1≤i≤5, 有

{x1+v1,x2+v2,x3+v3}lr=-{x2+v2,x1+v1,x3+v3}lr,

{x1,x2,x3+v3}lr={x1,x2,x3}+l(x1,x2)v3,

{x2,x1,x3+v3}={x2,x1,x3}+l(x2,x1)v3,

所以

l(x1,x2)=-l(x2,x1),

從而式(7)成立. 利用式(1),(12), 有

分別取vi≠0,vj=0, 1≤i≠j≤5, 得

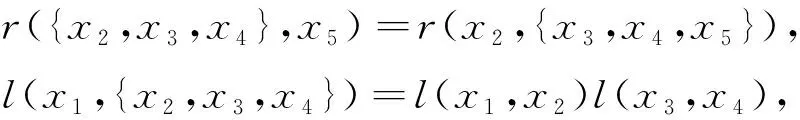
(13)

(14)

r(x1,x5)l(x2,x3)=l(x1,x2)r(x3,x5),

(15)

r(x1,x5)r(x2,x4)=r(x5,x1)r(x2,x4)+r(x1,x2)r(x5,x4),

(16)

r(x1,x5)l(x2,x3)=r(x5,x1)l(x2,x3)+r(x1,x2)l(x5,x3),

(17)

r(x1,x5)r(x3,x4)=r(x5,x1)r(x3,x4)-l(x1,{x5,x3,x4}),

(18)

r({x2,x3,x4},x5)=l(x5,{x2,x3,x4})+r({x5,x3,x4},x2),

(19)

l(x1,{x2,x3,x4})=r({x2,x3,x4},x1)-r(x1,x2)r(x3,x4).

(20)

由上述討論可知： 由式(13)可得式(7); 由式(19)可得式(10); 式(16)等價于式(14),(15),(17); 式(20)等價于式(13),(14),(19); 由式(13)可得式(8)； 由式(14),(15),(17)可得式(9); 由式(14),(15),(17),(18)可得式(11). 所以(l,r,V)是半結(jié)合3-代數(shù)A的雙模. 證畢.

定義線性映射τ:V∧V→V∧V, ?x1,x2∈V,τ(x1,x2)=(x2,x1).

定理4設A是半結(jié)合3-代數(shù),Ac是A的伴隨3-李代數(shù), (l,r,V)是半結(jié)合3-代數(shù)A的雙模, 則(V,ρ)是伴隨3-李代數(shù)Ac的模, 其中ρ=l-rτ+r.

證明: 由定理3和式(4)知, ?x1,x2,x3∈A,v1,v2,v3∈V, 有

所以(V,ρ)是3-李代數(shù)Ac的模. 證畢.

定理5設A是半結(jié)合3-代數(shù), 對?x,y∈A,L(x,y)和R(x,y):A×A→A分別為左乘映射和右乘映射, 則(L,R,A)是半結(jié)合3-代數(shù)A的雙模, 也稱為A的伴隨模.

證明： 應用定理3和定義1直接驗證可得結(jié)論, 故略.

定理6設(l,r,V)是半結(jié)合3-代數(shù)A的雙模, 則(l*,r*,V*)也是A的雙模, 其中V*是V的對偶空間,l*,r*:A×A→End(V*)分別為l和r的對偶映射, 即?x,y∈A,v∈V,ξ∈V*, 有

〈l*(x,y)(ξ),v〉=-〈ξ,l(x,y)(v)〉,

〈r*(x,y)(ξ),v〉=-〈ξ,r(x,y)(v)〉.

證明: 與定理 5的證明類似, 故略.

由定理5和定理6直接可得(L*,R*,A*)是半結(jié)合3-代數(shù)A的雙模.

定義1設A是半結(jié)合3-代數(shù), 如果線性映射θ:A?A?A→A*滿足: ?x,y,z,w,u∈A, 有

θ{x,y,z}=-θ{y,x,z},

θ{x,{y,z,w},u}=θ{x,y,{z,w,u}},

L*(x,y)θ{z,w,u}=-R*(x,u)θ{y,z,w},

則稱θ是半結(jié)合3-代數(shù)A的循環(huán)映射.

定理7設A是半結(jié)合3-代數(shù),θ:A?A?A→A*是A的循環(huán)映射, 則?xi∈A,ξi∈A*, 1≤i≤3,B=AA*按下列運算構成半結(jié)合3-代數(shù):

證明: 由式(7)～(11)及定理5知, 對任意xi∈A,ξi∈A*, 1≤i≤3, 有

綜上可知(AA*,{,,}θ)是半結(jié)合3-代數(shù). 證畢.