基于資源傳輸節點拓撲緊密性的鏈路預測方法

李英樂，何贊園，王 凱，許明艷

（中國人民解放軍戰略支援部隊信息工程大學信息技術研究所，鄭州 450002）

0 概述

鏈路預測是網絡科學的一個重要研究方向，其目的是通過分析網絡當前的拓撲結構和屬性信息，來預測網絡中不存在鏈接的節點之間出現鏈接的可能性［1］，對研究復雜網絡的演進機制具有十分重要的意義［2］，在生物網絡［3］和社交網絡［4］等現實網絡實踐中也具有很好的應用價值。

近年來，越來越多的學者對鏈路預測的方法進行了深入研究，并在多個方面都取得了一系列成果，特別是在基于網絡拓撲結構的鏈路預測方法上的進展較大。基于網絡拓撲結構的鏈路預測方法根據節點之間的鏈接關系計算節點之間的相似性，得到節點之間出現鏈接的可能性。節點相似性指標大體上包括全局相似性指標和局部相似性指標兩大類。局部相似性指標主要根據節點的共同鄰居來計算相似性，包括CN指標［5］、Salton指標［6］、AA指標［7］和RA指標［8］等。全局性指標是從整個網絡拓撲結構著眼計算節點相似性，主要有基于隨機游走的Cos+指標［9］、ACT 指標［10］、RWR 指標［11］和基于路徑的LP 指標［12］、LHZ-II 指標［13］、Katz 指標［14］。局部性指標僅考慮鄰居節點，其計算復雜度和精度較低；全局性相似指標考慮整個網絡結構，預測精度較高，但計算復雜度也較高，難以用于大規模網絡中。需要注意的是，由于RA 指標在局部相似性指標中取得相當高的預測精度，因此受到了廣泛的關注。但RA 指標僅從簡單的資源傳輸過程描述出發對其進行量化，忽略了傳輸節點周圍拓撲信息對資源傳輸節點傳輸概率的影響［15-16］。在現實網絡中，傳輸節點周圍拓撲的聚集程度與資源傳輸的效果具有相關性［17-18］，傳輸節點越聚集，資源的傳輸效果越好。

針對上述問題，本文提出一種基于資源傳輸節點拓撲緊密性的鏈路預測方法。研究資源傳輸過程中多跳節點資源的傳輸情況，確定重要傳輸節點，對傳輸節點聚類系數進行分析，基于聚類系數改進拓撲緊密性量化方法，并利用傳輸節點緊密性對共同鄰居傳輸資源進行參數調整，進而重新刻畫節點間相似性，給出資源傳輸節點拓撲緊密性指標。此外，在Precision 衡量標準下，利用多個實際網絡對所提指標進行有效性分析，以驗證該方法的預測效果。

1 相關工作

當前基于相似性的鏈路預測方法有很多，研究人員基于不同原理提出多種預測指標，本節對幾種知名預測指標及網絡資源傳輸相關指標簡要介紹如下：

1）CN 指標［5］。LORRAIN 等人直接利用共同鄰居的數目衡量節點x和y的相似度，該方法復雜度低，在集聚性較高的網絡中表現較好，但在稀疏網絡中表現較差。Γ（x）為節點鄰居的集合，表示為：

2）AA 指標［7］。根據節點對共同鄰居的重要程度不同，ADAMIC 等人利用高度懲罰機制對共同鄰居加權，權值為節點度對數的倒數，表示為：

3）CAR 指標［17］。在CN 的基礎上考慮了共同鄰居之間存在鏈接的情形，該方法在集聚性較高的網絡中表現較好，CAR 指標可表示為：

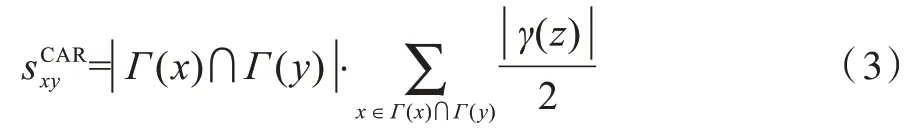
4）LP 指標［12］。呂林媛等人在共同鄰居（即2 階路徑）基礎上，綜合考慮了3 階路徑對節點相似性的影響，LP 指標可表示為：

其中，S為相似度矩陣，A是鄰接矩陣，(An)xy表示節點x和y之間長度為n的路徑數目，α為調節參數。該方法是預測效果與計算復雜度的合理折中，效果好于CN 指標。

5）Katz 指標［14］。KATZ 等人從網絡全局角度充分考慮節點間所有的路徑數目量化節點間的相似度，具有很好的預測精度，但復雜度較高，表示為：

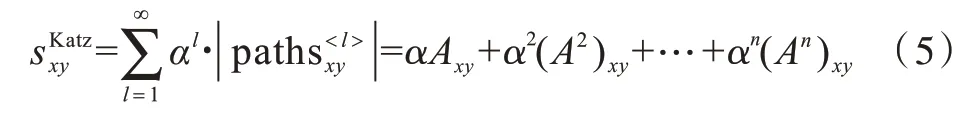
6）ACT 指標［10］。KLEIN 等人將一個隨機游走的粒子從一個節點x游走至另一個節點y所需要走的平均步數，作為兩節點產生連接的可能性，提出平均通勤時間指標，表示為：

7）Cos+指標［9］。FOUSS 等人在基于隨機游走的基礎上，提出余弦相似性指標，在矩陣L+計算2 個向量之間的相似性：

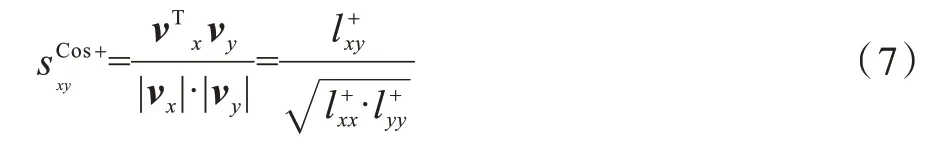
8）RA 指標［8］。周濤等人基于資源傳輸原理，認為共同鄰居傳遞資源的多少和其路徑上共同鄰居的節點度成反比，RA 指標具體表示為：

9）ERA 指標［19］。劉樹新等人在RA 指標的基礎上，詳細分析節點間多跳的局部路徑傳輸的資源，提出了擴展的資源分配ERA 指標，具體表示為：

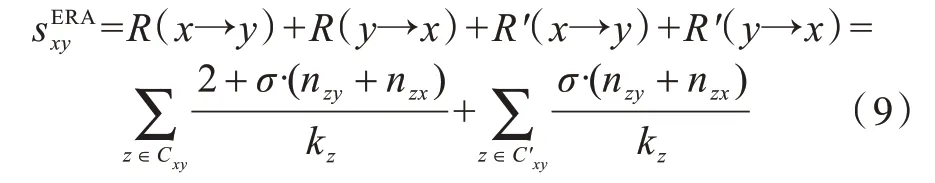
其中，參數σ表示多跳路徑資源對相似性的貢獻，當σ=0 時，該指標退化為RA 指標。

10）EP 指標［20］。王凱等人考慮資源傳輸路徑有效程度對傳輸性能的影響，分析了潛在的資源傳輸路徑有效性并對雙向資源傳輸量進行刻畫，EP 指標具體表示為：

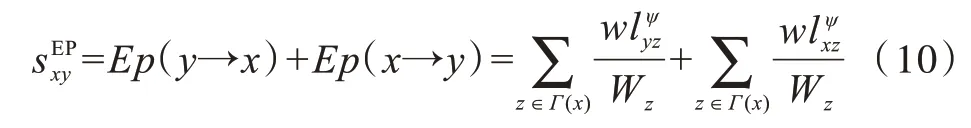
其中，Wz表示節點z所有連邊的路徑有效量化值之和，wlij表示節點i、j之間的有效資源傳輸量。

11）QN 指標［21］。王凱等人在研究路徑傳輸有效性基礎上，分析傳輸路徑的資源承載能力，提出資源承載度及相應的預測方案，具體表示為：

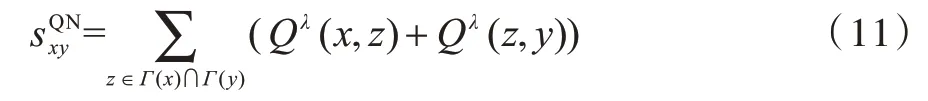
其中，Qλ（i，j）表示節點i、j之間量化的資源承載能力。

綜上可見，資源傳輸原理是節點相似性刻畫的重要參考，其不僅應從傳輸過程分析，而且在傳輸路徑、局域拓撲等方面有更多待研究之處。

2 資源傳輸節點拓撲緊密性鏈路預測方法

2.1 資源傳輸節點拓撲緊密性分析與量化

研究發現，網絡演進時連邊的變化會影響到網絡中的信息的傳播［23］，同時網絡中信息的傳播也會影響到連邊的變化［24］，此兩者具有相關性［25］。任意2 個未連接點之間的資源傳輸需要經過多跳節點進行，共同鄰居節點作為最短跳的資源傳播節點，是資源傳輸過程的核心。圖1 所示為不同類型資源傳輸節點在資源傳輸過程中的作用（圖中僅以節點x傳輸一定的資源至節點y的過程為例）。

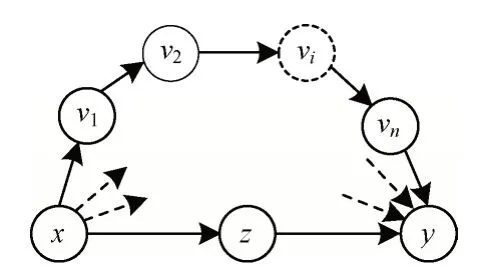
圖1 不同類型資源傳輸節點在資源傳輸中的作用Fig.1 Effect of different types of resource transmission nodes in resource transmission

從圖1 可以看出，在多跳路徑傳輸中，隨著路徑上節點數目的增加，資源傳輸過程趨于復雜，資源量的傳輸“衰落”現象也越來越明顯，導致節點x到節點y的資源傳輸量也會以一定的比例逐步減少。而僅經過兩跳傳輸的共同鄰居節點z，其傳輸資源的效率和確定性明顯高于其他傳輸節點。因此，在資源傳輸過程中，共同鄰居是資源傳輸的核心節點，發揮著關鍵作用。在資源傳輸的后續分析中，將重點針對核心資源傳輸節點共同鄰居。

資源傳輸指標（RA）是直接利用核心傳輸節點共同鄰居進行資源傳輸過程分析，然后對任意2 個未連接節點進行相似性刻畫。該方法效果較好，但現實網絡中核心傳輸節點共同鄰居周圍拓撲結構較為復雜，僅利用節點度對其進行資源傳輸量的刻畫難以更加有效地量化傳輸過程。共同鄰居節點周圍拓撲結構的緊密性會對資源傳輸有著較大影響，如圖2 所示。對于節點x和節點y的共同鄰居節點zn，其周圍存在鄰居節點｛v1，v2，v3，v4，v5｝和許多連邊構成了相對稠密的局部結構，這對于資源傳播具有很大的促進作用。為量化局部結構對節點間資源傳輸的作用，需要分析刻畫傳輸節點周圍拓撲結構的資源傳播緊密性。

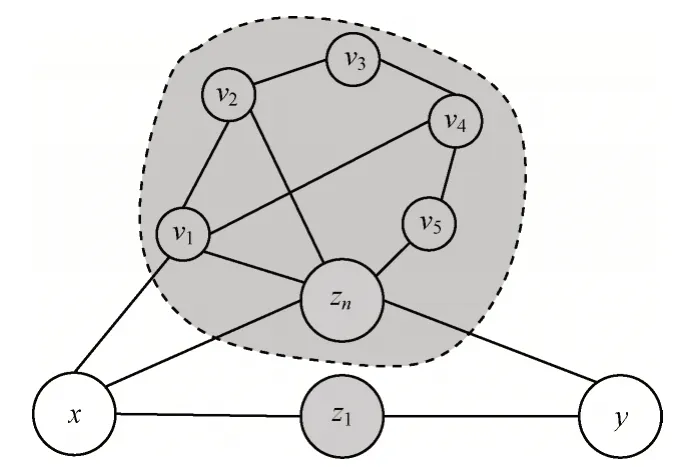
圖2 資源傳輸節點周圍拓撲結構示意圖Fig.2 Schematic diagram of topology around resource transmission nodes

網絡節點的聚類系數是刻畫網絡局部拓撲結構緊密性的重要參數［26］。對于網絡中任意一個節點i，有ki個鄰居節點。若所有鄰居節點間兩兩互聯，則所有連邊數目表示為ki（ki-1）/2，此時網絡鄰居節點的緊密性最大。在正常情形下，節點i的聚類系數可以表示為：

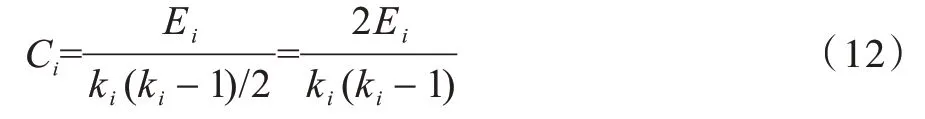
其中，Ei表示節點i的所有鄰居節點間實際存在連邊的數目。節點聚類系數會隨著鄰居節點連邊數目不斷增加，如圖3 所示。圖3（a）中鄰居節點之間無任何連接，此時節點i的拓撲集聚性最低，Ci=0；圖3（b）中鄰居節點之間存在一條連接，此時聚類系數Ci=2×1/（4×3）=1/6；圖3（c）中鄰居節點之間的連接大幅度增加，此時拓撲間關系更加緊密，聚類系數為Ci=2×3/（4×3）=1/2；圖3（d）中所有鄰居節點都存在連接，局部拓撲集聚性達到最大，此時聚類系數為Ci=1。可以看出，網絡節點聚類系數一定程度上表征了獨立節點周圍拓撲緊密性。然而，不同于獨立節點僅考慮局部拓撲結構，對于一對未連接節點的核心資源傳輸節點，其資源傳輸緊密性的刻畫需要考慮資源傳輸節點周圍拓撲結構對資源傳輸過程的影響，而且直接使用聚類系數難以表征不同鄰居節點對傳輸資源緊密性的作用。

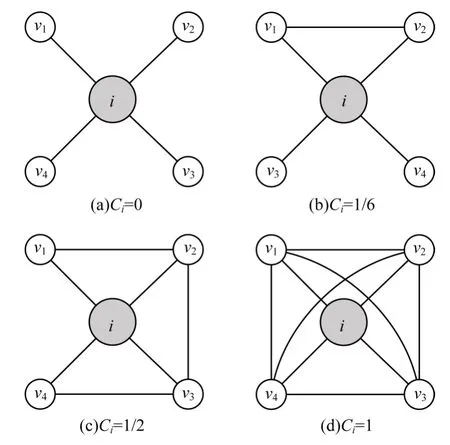
圖3 獨立節點不同拓撲結構下的緊密性分析Fig.3 Tightness analysis of independent nodes under different topology

為分析在不同拓撲結構下資源傳輸節點周圍局部拓撲對節點間資源傳輸的影響，進而刻畫資源傳輸節點拓撲結構的緊密性，本文引入多個局部拓撲結構進行對比分析，如圖4 中的4 個網絡結構中均存在一對未連接的節點x和y，以及待分析的資源傳輸節點zi。下文將對比分析zi周圍不同拓撲結構對于節點x和y資源傳輸過程的影響，即對資源傳輸節點緊密性的影響。對于圖4（a）和圖4（b），傳輸節點zi具有相同數目的鄰居節點，但后者鄰居節點之間連邊數目明顯高于前者，因此從節點x和y資源傳輸的角度，后者傳輸節點zi的資源傳輸緊密性明顯高于前者；對于圖4（b）和圖4（c），傳輸節點zi既具有相同數目的鄰居節點，也具有相同數目的鄰居連邊，不同的是前者是｛v1，v3｝和｛v2，v3｝，而后者是｛v1，x｝和｛v1，z1｝。雖然從聚類系數角度，圖4（b）和圖4（c）的集聚性相同，但是很明顯后者zi的鄰居節點v1的連邊為資源傳輸提供了更大的可能（對比來看，后者鄰居節點v1為節點x和y提供了更少跳數的稠密拓撲傳輸結構），因此，從節點x和y資源傳輸的角度，圖4（c）傳輸節點zi的資源傳輸緊密性高于圖4（b）；對于圖4（c）和圖4（d），傳輸節點zi具有相同數目的鄰居節點，但后者具有更多鄰居連邊和有效鄰居節點v4。因此，從節點x和y資源傳輸的角度，圖4（d）傳輸節點zi的資源傳輸緊密性高于圖4（c）。

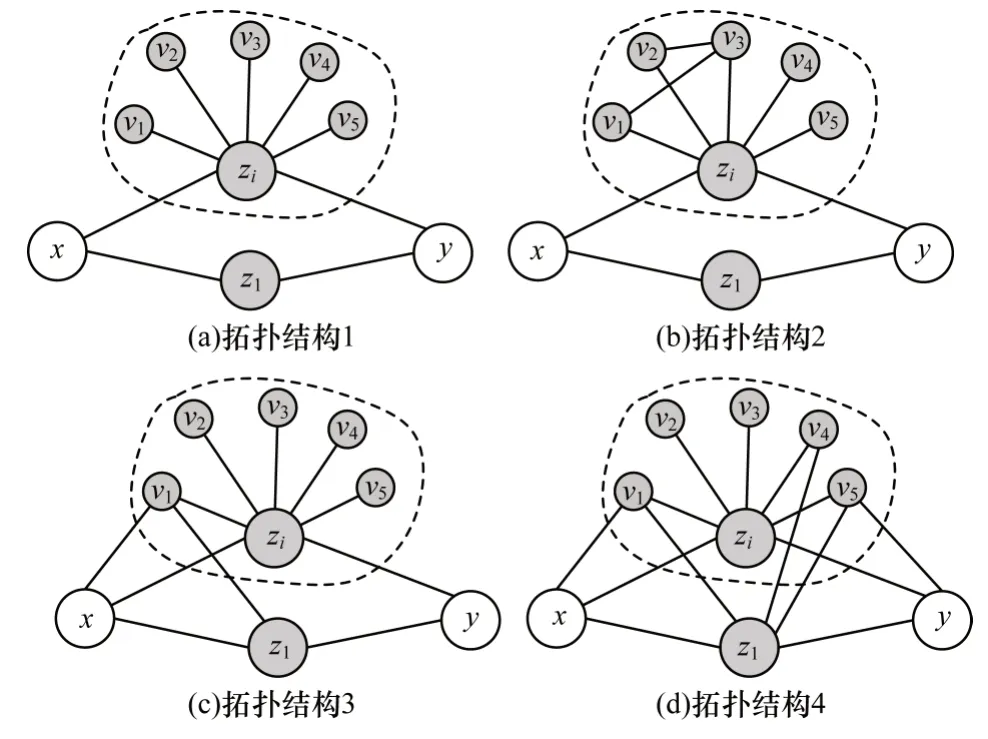
圖4 不同資源傳輸節點周圍拓撲結構Fig.4 Topology around different resource transmission nodes

通過上述分析可以看出，傳輸節點的鄰居在資源傳輸緊密性的刻畫上發揮著不同的作用。對于資源傳輸始發、終結節點x和y，若傳輸節點zi的鄰居與其存在連接，則其對于資源傳輸的貢獻較大，如圖5中的v1、v2、v3。與之相反，若傳輸節點zi的鄰居與始發、終結節點并無連接，其對于資源傳輸的貢獻非常小，考慮到路徑上資源的“衰落”，可以忽略其對于節點資源傳輸緊密性的影響，如圖5 中的v4、v5。因此，為從資源傳輸的角度更好地刻畫傳輸節點的緊密性，對傳輸節點的鄰居中對緊密性貢獻較大的鄰居進行定義。

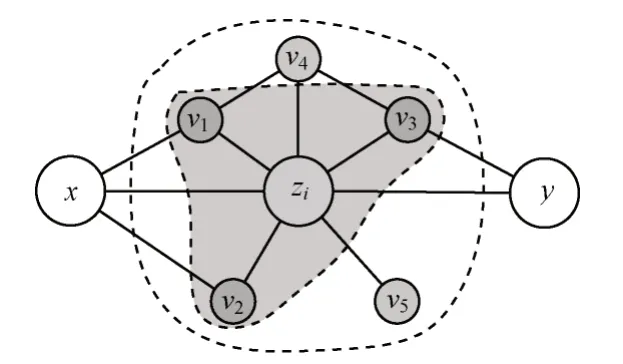
圖5 資源傳輸節點周圍拓撲結構示意圖Fig.5 Schematic diagram of topology around resource transmission nodes

定義1（資源傳輸節點的緊密鄰居） 網絡中任意一對未連接的資源傳輸始發、終結節點x和y，共同鄰居節點z是其核心傳輸節點。對于傳輸節點z的所有鄰居節點，其緊密鄰居包含始發、終結節點x和y，主要囊括與其存在直接連邊的鄰居節點。傳輸節點z的緊密鄰居集合可表示為：

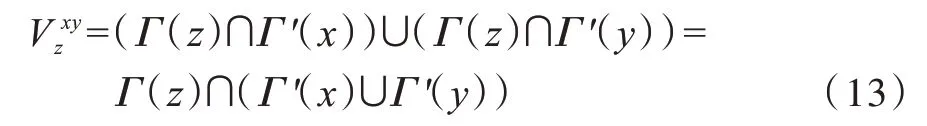
其中，Γ（z）為傳輸節點z的所有鄰居節點集合，Γ'（x）、Γ'（y）為包括自身節點x、y及其所有鄰居節點的集合。圖6 所示為資源傳輸節點的緊密鄰居，對于資源傳輸始發、終結節點x和y，其資源傳輸節點z的緊密鄰居為：

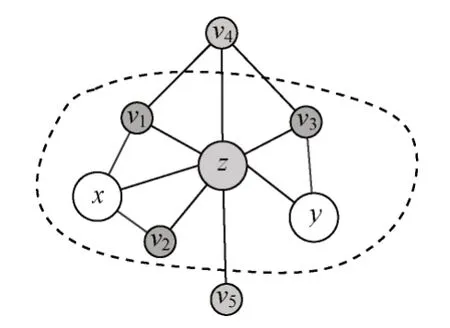
圖6 資源傳輸節點的緊密鄰居示意圖Fig.6 Schematic diagram of tight neighbors of resource transmission nodes

對于同樣的網絡結構，若其資源傳輸的始發、終結節點發生了變化，其緊密鄰居也會發生變化。若圖6 中資源傳輸始發、終結節點是v4和v5，其資源傳輸節點z的緊密鄰居為：

在對資源傳輸節點z的緊密鄰居進行定義后，便可以對其緊密性進行量化，本文基于聚類系數，從緊密鄰居的角度定義傳輸節點的緊密性。

定義2（資源傳輸節點拓撲緊密性） 網絡中任意一對未連接的資源傳輸始發、終結節點x和y，共同鄰居節點z是其核心傳輸節點。對于傳輸節點z，其資源傳輸拓撲緊密性量化為緊密鄰居間實際連邊數目占比緊密鄰居最大連邊數目，即：

具體表示為：

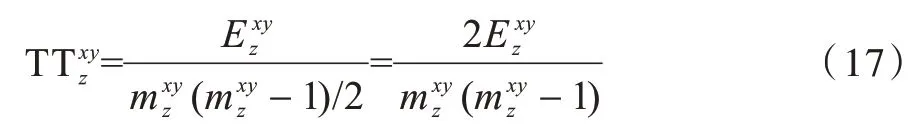
2.2 資源傳輸節點拓撲緊密性指標

對資源傳輸節點拓撲緊密性進行量化后，便可以基于拓撲緊密性分析節點之間的相似性，進而預測任意節點之間存在的可能性。在一般情況下，與資源分配指標RA 相似，可以直接利用傳輸節點拓撲緊密性對資源傳播進行加成：

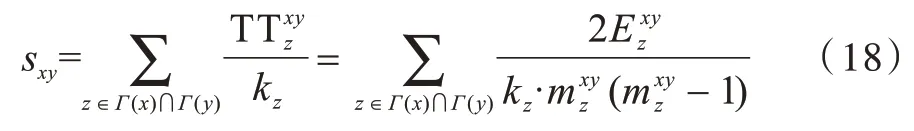
式（18）直接利用存在相似度量化上的問題，若資源傳輸節點z的緊密鄰居之間并無連接，其相似度則量化為0。該量化方法會一定程度上忽視共同鄰居節點本身的資源傳輸能力。因此，在刻畫資源傳輸節點拓撲緊密性指標時，需要同時考慮兩個方面：一方面考慮關鍵資源傳輸節點本身的資源傳輸能力；另一方面需要考慮該資源傳輸節點拓撲緊密性對資源傳輸能力的影響。如圖7 所示，若資源從節點x傳輸指定資源到端節點y，則該傳輸過程的資源量與共同鄰居節點本身資源傳輸和其拓撲緊密性對資源傳輸影響相關。

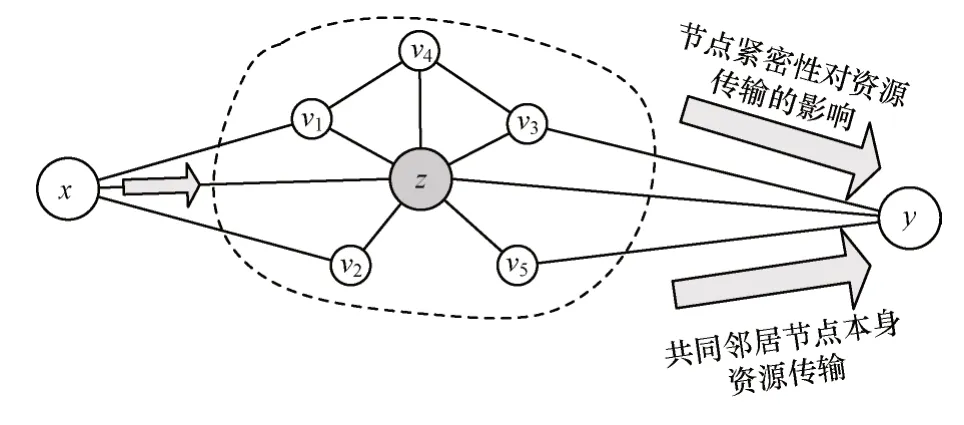
圖7 資源傳輸節點拓撲緊密性指標示意圖Fig.7 Schematic diagram of tightness index of resource transmission node topology

定義3（資源傳輸節點拓撲緊密性指標） 對于一個無向網絡G（V，E），其中網絡中任意存在兩個節點x和y，從網絡中關鍵資源傳輸節點的局部拓撲出發，即共同鄰居節點拓撲緊密性的角度，節點x和y之間的相似性可量化為所有共同鄰居節點本身傳遞資源量與其拓撲緊密性加成資源量之和，具體表示為：

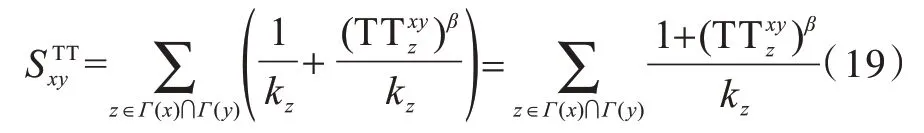
其中，β為調節參數，用于調整不同網絡中資源傳輸節點拓撲緊密性對資源傳輸量的影響程度，1/kz表示共同鄰居節點本身傳遞資源量，而表示拓撲緊密性加成資源量。當β=0 時，資源傳輸節點拓撲緊密性指標（TT 指標）與資源分配指標RA 相同。而對于圖7 所示的拓撲結構中

3 網絡數據集

為了驗證基于傳輸節點拓撲緊密性的鏈路預測方法的有效性，本文選取了多個不同類型的實際網絡進行實驗，對具體網絡數據分別介紹如下：

1）爵士音樂家合作網絡Jazz［27］：一種表示爵士音樂家之間的合作關系的網絡，其中音樂家用網絡節點表示，音樂家之間的合作關系用網絡中的連邊表示。

2）食物鏈網絡FWEW［28］：一種生活在Everglades Graminoids 濕季的69 種生物組成的網絡，不同生物用網絡節點表示，生物之間的捕食關系用網絡的邊表示。

3）美國航空線路網絡USAir［29］：網絡的節點代表不同的機場，網絡中的連邊代表機場之間有直達航線。

4）線蟲神經網絡CE［30］：線蟲神經元用網絡節點表示，線蟲的神經元突觸或其之間的連接用網絡的連邊表示。

5）郵箱通信網絡Email（EM）［31］：一種規模為中型的工廠工人之間的郵箱通信網絡，工人的郵箱地址用網絡節點表示，不同工人之間的郵件往來用網絡連邊表示。

6）線蟲新陳代謝網絡Metabolic［32］：秀麗隱桿線蟲的新陳代謝網絡，節點表示代謝物，而連邊表示它們之間的相互作用關系。

7）Infectious（Infect）［33］：2009 年，在柏林科學美術館的表演“Infectious：Stay away”中人們面對面行為的網絡，參與的人員用網絡節點表示，人與人之間的溝通用連邊表示。

8）mac-animal［34］：一種62 個成年雌性日本獼猴的支配行為有向網絡，節點表示獼猴，網絡連邊表示左側節點對右側節點的支配行為。

上述網絡數據集的具體網絡統計特征參數如表1 所示。表1 主要包含網絡節點數目（|V|）、網絡中邊的數目（|E|）、網絡平均聚類系數（C）、網絡平均節點度和網絡平均最短路徑。在后續網絡數據實驗中，本文設置訓練集合ET中連邊數目占比為0.9，測試集EP的連邊占比為0.1，此次每個數據測試點的結果均為20 次實驗的平均值。

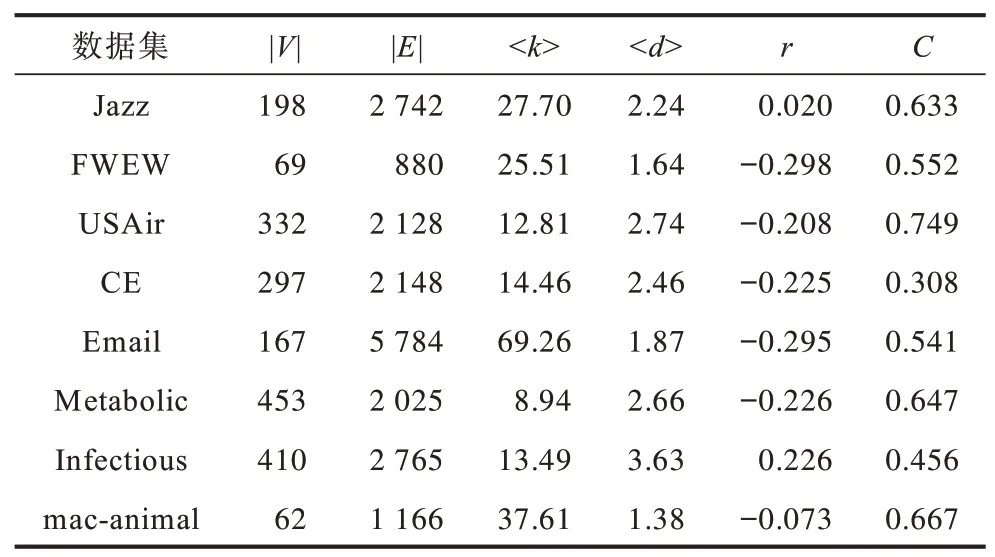
表1 實驗數據集統計信息Table 1 Statistical information of experimental datasets

4 實驗結果與分析

為驗證資源傳輸節點拓撲緊密性指標的有效性，本文在多個不同類型網絡中進行實驗驗證。在實驗研究中，由于該指標主要針對Precision 指標，因此重點對Precision 結果進行實驗。具體地，首先實驗分析了不同網絡中調節參數對TT 的Precision 結果的影響，然后與現有指標進行對比，分析TT 的實驗效果和有效性，并給出現實網絡應用時的合理使用建議值。

4.1 Precision 結果的參數影響分析

資源傳輸節點拓撲緊密性指標的具體相似性刻畫，利用了參數β調節不同網絡中資源傳輸節點拓撲緊密性的影響程度。圖8 顯示了不同網絡中參數β對資源傳輸節點拓撲緊密性指標預測結果的影響。

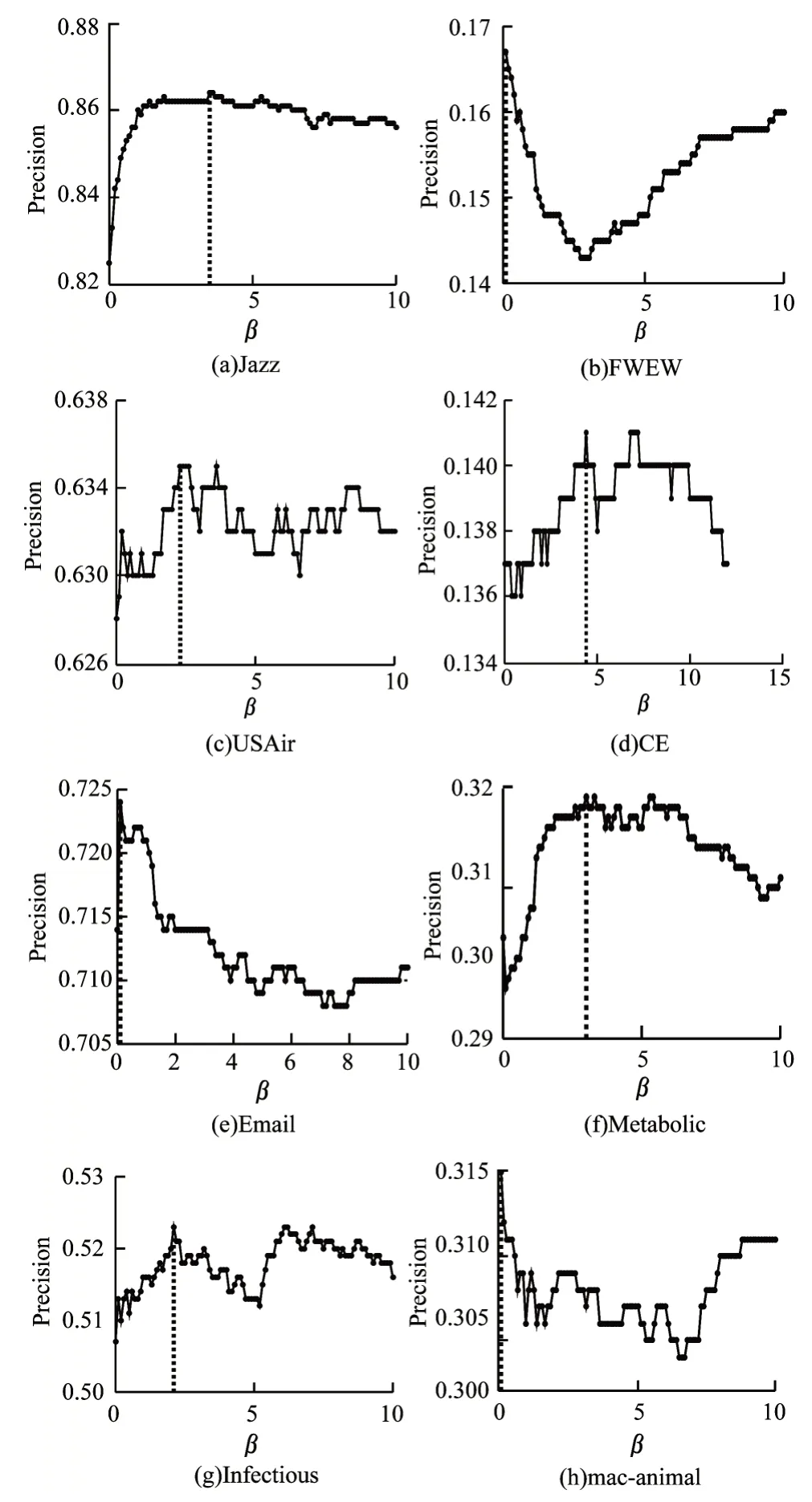
圖8 TT 指標Precision 結果隨參數變化示意圖Fig.8 Schematic diagram of TT index Precision results with parameters changes

可以看出，不同網絡中參數β對TT 指標的影響較大，在Jazz 和Metabolic 網絡中隨著β值的增大，在β=0 處迅速增長，說明傳輸節點拓撲緊密性影響非常明顯。當Precision 值達到較高值后，隨參數持續穩定，說明此時傳輸節點拓撲緊密性強度的增大對節點間相似性的貢獻不再明顯增大；在FWEW 和macanimal 網絡中，參數β對TT 指標的影響較為復雜，隨著β值的增大，Precision 值逐漸下降到極點后逐步上升，說明較低的拓撲緊密性強度對于相似性刻畫促進作用逐漸下降，而到達較大強度后會逐漸增強其影響力；USAir 和CE 網絡相似，在參數β較小時其Precision 值上升至最大值，然后隨著參數β的增大呈現輕微下降趨勢；與其他網絡不同，在Email 網絡中，在參數β接近0 時Precision 值呈現急劇上升趨勢，表明較低的傳輸節點拓撲緊密性強度便可以產生較好的效果。同樣，當達到最高點后，隨著參數β的增大，呈現快速下降趨勢，也說明了此時傳輸節點拓撲緊密性強度對其影響正在逐漸降低；在Infectious 網絡中，當參數β較小時Precision 呈現持續上升態勢，到達最大值頂點后逐步下降，而后又呈現上升，說明傳輸節點拓撲緊密性強度在不同階段對其影響各異。總之，在多數網絡中，當參數β較小時，傳輸節點拓撲緊密性強度對Precision 結果促進作用較強，部分網絡中提升幅度較大且相對穩定，說明傳輸節點拓撲緊密性對相似度刻畫具有一定的有效性。

4.2 Precision 結果對比分析

為進一步研究分析資源傳輸節點拓撲緊密性指標的有效性和特點，本文選取了8 個相似性指標進行對比分析。對比指標方法主要包括局部相似性和全局相似性指標，其中局部相似性指標包括共同鄰居指標CN、資源分配指標RA、AA 指標和考慮共同鄰居相互關系的CAR 指標，全局相似性指標包括全路徑指標Katz、平均通勤時間ACT 和余弦相似性指標Cos+，還包括介于局部和全局之間的局部路徑指標LP。

表2 為多個不同類型網絡中TT 指標與現有指標的Precision 結果對比情況。其中，（a）可調參數α=0.001，（b）可調參數α=0.01。

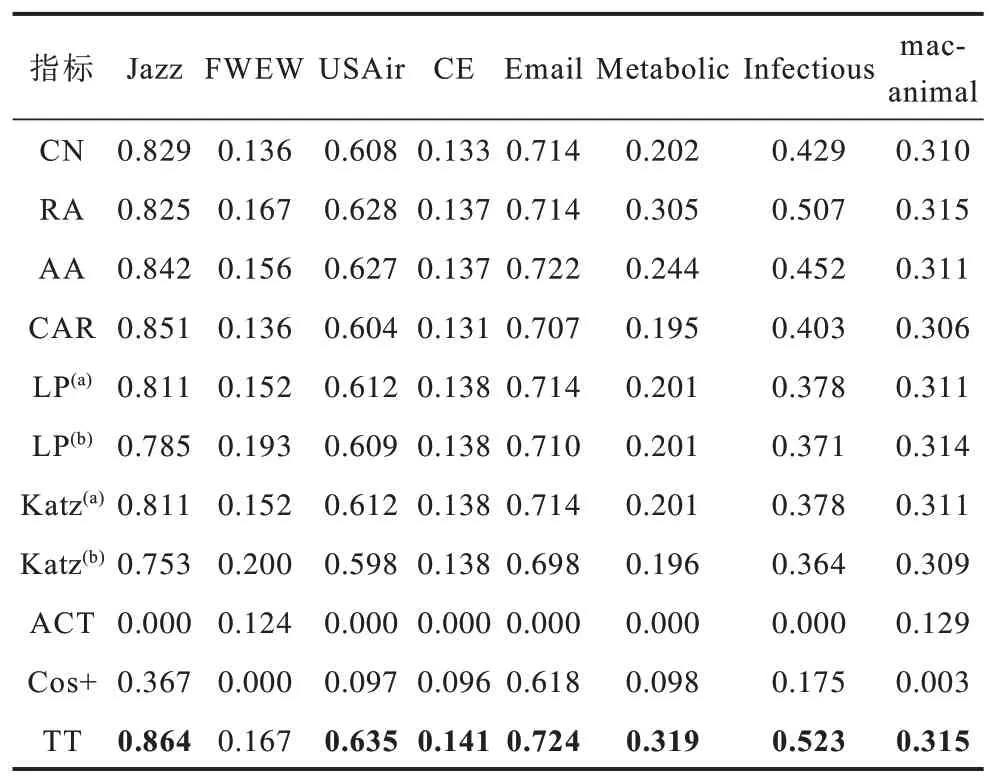
表2 Precision 結果對比分析Table 2 Comparative analysis of Precision results

從表2 可以看出，相比其他的相似性指標，總體上TT 指標具有較高的預測精度，8 個網絡中有7 個網絡TT 指標的Precision 值最高（見粗體數字），只有在FWEW 網絡中排名第三，這在一定程度上說明了資源節點拓撲緊密性對節點間相似性刻畫的有效性。作為最簡單的共同鄰居指標CN，由于僅考慮了共同鄰居的數目，其Precision 預測結果具有一定的效果，但相比其他相似性方法，大多數網絡中CN 的預測結果略低（除在Email、Metabolic 和Infectious 網絡中，CN 的Precision 高于CAR、LP、Katz）。資源分配指標RA 通過利用資源分配過程計算節點間傳輸的資源量進行量化節點間相似性，其復雜度較低但效果明顯好于一般局部相似性指標，尤其是在FWEW、USAir、CE、Metabolic、Infectious 和macanimal 等網絡中，部分甚至高于全局相似性指標LP或Katz。與RA 指標類似，AA 指標利用共同鄰居的節點度對共同鄰居進行加權，其效果在多數網絡中好于共同鄰居指標，部分網絡如Jazz、USAir、CE、Email、Metabolic 和Infectious 中其結果好于全局指標。CAR 指標考慮了共同鄰居之間存在的部分連接對相似性的影響，其效果明顯好于共同鄰居指標，但在多數網絡中比RA 和AA 效果略差。LP 和Katz 是基于長路徑的相似性指標，在多數網絡中效果較好且相對穩定，尤其是在FWEW、CE、Email 和macanimal 網絡中效果最好。平均通勤時間ACT 指標是基于隨機游走的相似性指標，不過在Precision 衡量標準下，多數網絡中普遍較低，許多Precision 值甚至接近于0，這可能是與ACT 指標更多地適用于AUC衡量標準，而不適用于Precision 標準。余弦相似性指標Cos+同樣是基于隨機游走的相似性指標，相比ACT 其效果有了一定的提升，但與其他相似性指標相比，其總體效果較差。ACT 和Cos+的Precision 效果分析結果表明，部分基于隨機游走的相似性指標更多地傾向于AUC 衡量標準，難以適應于Precision衡量標準。在考慮了資源傳輸節點拓撲緊密性后，TT 指標在8 個網絡中表現普遍較好。多個網絡中如在Jazz、USAir、Email 和Infectious 中，其Precision 的提高幅度較高，明顯高于其他局部和全局相似性指標。在mac-animal 中，TT 指標與RA 相似，說明了當前網絡中資源傳輸節點拓撲緊密性的影響較低，其設置參數為0。在現實網絡的鏈路預測應用中，建議參數設置為11.1，各個網絡中表現普遍較高。此外，本文所提方法時間復雜度介于共同鄰居指標CN 和局部路徑指標LP 之間，復雜度相對較低，可以應用于大規模復雜網絡鏈路預測。

綜上所述，本文方法能夠同時在2 個衡量指標AUC 和Precision 下取得較好的效果。AUC 和Precision 作為鏈路預測2 個重要但角度不同的衡量標準，在一定程度上說明了本文方法的普適性較高。此外，本文方法在8 個不同網絡的實驗預測效果相對較高，也驗證了其在不同網絡數據集上的普遍應用價值。

5 結束語

本文根據傳輸節點周圍拓撲緊密性對資源傳輸節點傳輸概率的影響，結合節點拓撲緊密性的特點，提出一種基于資源傳輸節點拓撲緊密性的鏈路預測方法。從資源傳輸過程分析重要的傳輸節點，重點研究傳輸節點周圍拓撲關系的量化問題，以節點聚類系數為突破點，通過分析當前聚類系數在刻畫資源傳輸節點有效性中存在的問題，提出相應的資源傳輸緊密性量化方法，并基于資源傳輸緊密性，對任意未連邊節點間的資源傳輸量進行刻畫，給出資源傳輸節點拓撲緊密性指標。在多個實際網絡數據中的實驗結果表明，本文相似性指標適合于Precision標準，且相比其他指標具有較好的預測效果。本文方法和思路可以為資源傳輸過程的刻畫提供一種新思路和借鑒。在后續研究中，將通過探討傳輸路徑有效性對資源傳輸過程的影響，進一步豐富和拓展基于資源傳輸過程的鏈路預測方法。