基于遺傳算法的醫療設備更新決策優化

呂小平

興化市人民醫院后勤保障部 （江蘇泰州 225700）

醫療設備管理部門的成本預算項目中最常見的是醫療設備的購置計劃，而評估未來醫療設備的采購需求則是其中的重要工作之一[1-2]。未來的需求計劃應根據每臺設備的使用壽命制定出醫療設備更新的優先級列表[3-4]。大多數醫院缺乏足夠資金來滿足醫療設備的所有更新要求，因此，醫療設備管理部門應合理分配被批準用于更新設備的資金[5]。在預算約束的情況下，通過制定優化目標、建立優化模型并采取適當的方法，可使亟需更新設備的數量獲得最大值，即在購置預算范圍內盡可能多地更新設備。

文獻[6]基于故障樹分析法，通過建立定量模型來制訂醫療設備的更新決策，再依據更新因子的取值范圍，將91臺監護儀以生命狀態進行分類，最終得出結果，37.36%的監護儀（34臺）需進行更新。本研究針對此34臺監護儀，以設備更新數量最大值為基礎，建立優化模型（該優化模型屬非線性整數規劃問題），為基于故障樹分析法的設備更新決策模型提供進一步的科學依據。遺傳算法是模擬生物界自然選擇和自然遺傳機制的隨機化搜索算法，是一種可尋求全局最優解的高效優化方法[7-8]。因此，本研究采用遺傳算法對醫療設備更新決策模型進行優化研究，并在考慮醫療設備管理部門的更新預算限制和醫療設備更新優先級的基礎上，建立優化設備更新決策的模型，并以此為根據調整數量來為醫療設備年度更新計劃的制訂提供參考。

1 遺傳算法的改進和設計

1.1 算法的流程

傳統的遺傳算法存在易產生早熟收斂等問題，主要原因為交叉概率（Pc）、變異概率（Pm）等參數設定的是經驗值。對不同的研究問題而言，各參數的取值有不同的要求，其取值與所研究問題的類型存在直接關系。因此，在醫療設備更新決策的優化研究中，需設計適當的遺傳算法。本研究以遺傳算法中設置參數優化作為改進思路，如種群大小、遺傳代數、Pc和Pm等，從而使改進的遺傳算法加速收斂以避免冗余運行，提高算法的搜索質量。

改進遺傳算法的開發遵循遺傳算法的一般步驟，即從隨機選擇的種群開始，通過評估目標函數選擇產生新的種群，然后交叉和變異算子產生新的后代，從而得到最合適的解決方案。這個過程是可重復的，直至找到滿足條件的最優解后終止計算。本研究中，最優解的方案為產生最大數量且具有最小標準偏差的運算結果。根據更新優先級和預算約束，使用設備的更新因子、購置價格和可用更新預算初始化算法，然后再按照遺傳算法的一般步驟進行運算。擬議的算法流程介紹如下：（1）輸入更新因子、設備購置價格和更新預算；（2）設置遺傳進化次數計數器t=0；（3）初始化控制參數，隨機生成初始種群；（4）個體評價，計算初始種群的適應度，選擇優良個體組成種群P（0）；（5）選擇、交叉、變異運算；（6）種群P（0）經過選擇、交叉、變異運算之后，計算個體的適應度，選擇適應度高的個體組成下一代種群；（7）終止條件判斷，若遺傳次數t＜T，則返回（5），進行選擇、交叉、變異操作，循環往復，若t=T，則以進化過程中所得到的具有最小標準偏差的個體作為最優解，解碼后得出結果輸出，終止計算，見圖1。

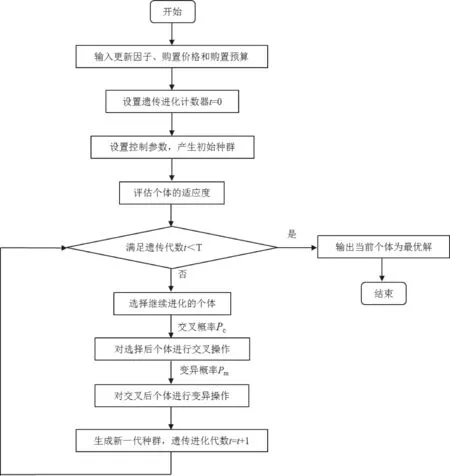
圖1 改進遺傳算法的流程

1.2 目標函數的建立

在優化模型中，目標函數是對涉及優劣解進行比較的指標，本研究中的目標函數可直接作為適應度函數使用。從設備更新角度看，設備的更新因子越大，其更新優先權重越大；另一方面，更新因子的取值又直接影響購置預算的選定，更新因子大的設備數量越多，需更新的設備購置價格越高，那么需用于設備更新的預算則越多。因此，在可用預算的限制范圍內，應首先更新優先權最高的醫療設備，以降低可能的風險并防止醫院成本預算的增加；同時，應優先購置價格低的設備以避免消耗大量更新預算。為根據可用預算優化設備更新列表，需首先預估新設備的購置價格以便將其與更新預算比較，從而使得預算范圍內的設備數量獲得最大值。模型的目標函數和約束條件如下：

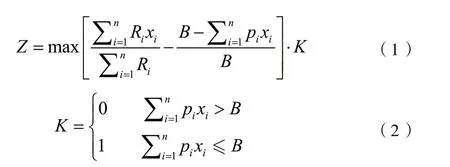
其中，Z 為目標函數； Ri為第 i 臺設備的更新因子；xi為設備列表中第i 臺設備的決策變量； pi為第i 臺設備的購置價格；B 為醫療設備管理部門的設備更新預算；K 為資金預算約束因子；n 為設備的總數量。

采用遺傳算法對醫療設備更新決策問題進行分析時，適應度函數的優劣同樣影響算法的收斂性。同時，因遺傳算法涉及隨機運算，因此，每次的運算結果是不完全一樣的。本研究對改進的遺傳算法運行20次以優化算法的運行結果，并通過一組描述性統計方法，將算法的運行結果與計算得到的目標函數的平均值進行比較，根據標準偏差找出具有最優控制參數的最優解（最優解的方案為產生最大更新數量且具有最小標準偏差的輸出值），標準偏差的計算公式如下：

其中，STD 是標準偏差，σi是第i 次算法運行得到的適應度值，μ 是σ 的平均值，n 是算法執行的次數，此算法中為運行20次。標準偏差值越小，則表示該算法的穩定性越高，據此判斷所選參數是否合適。

1.3 遺傳算法控制參數的設置

通過分析并比較不同的種群大小、遺傳代數、Pc和Pm等控制參數的組合對模型尋優過程的影響，得到醫療設備更新預算決策模型的最優組合控制參數。根據遺傳算法的控制參數取值[9]和更新優化模型的特點，本研究對種群大小、遺傳代數、Pc和Pm進行了適當的組合，見表1。

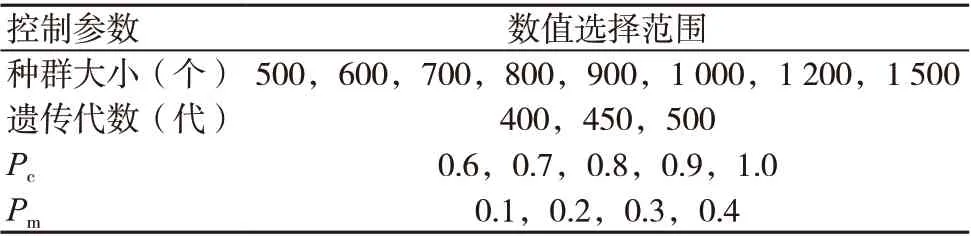
表1 算法控制參數設置

文獻[6]研究結果顯示，91臺監護儀中有37.36%應更換，即有34臺監護儀處于更換的優先級列表中。根據我院醫療設備管理部門每年的資金預算和實際情況，可用的更新預算相較于所調查醫療設備的預估購置預算要低20%，即當本年度醫療機構的監護儀購置預算為75萬元時，那么設備的更新預算為60萬元，而不同規格型號的監護儀的購置價格為2萬～5萬元。用34臺監護儀設備的基本信息（如更新因子等）及設備的購置價格和更新預算作為模型的輸入參數，該算法的每種控制參數組合在MATLAB 中運行20次，以找出該算法的最佳控制參數[10-11]。

在遺傳算法中，較大的種群有助于增加群體的多樣性，防止算法過早收斂，產生早熟現象。但群體規模增大，會降低算法的運行速度，因此，需在Pc和Pm不變的情況下，運行不同的種群大小和遺傳代數對模型進行求解。為增加種群多樣性，避免出現過早收斂，Pm的最大值取0.4，Pc的最小值取0.6。圖2（a）表示不同遺傳代數的情況下，初始種群和最優解之間的關系。結果表明，遺傳代數為500代，種群大小為600、1 500個時，目標函數能得到最多的最優解個數。種群大小為600個時，標準偏差最小，為0.0384，因此，得出最優的遺傳代數為500代，種群大小為600個。然后使用種群大小和遺傳代數的最優控制參數，以不同的Pc運行不同的Pm從而確定它們的最佳值。圖2（b）表示不同 Pc和 Pm與最優解的關系，當 Pc為0.9，Pm為0.4和0.1時，該算法得到最優解的個數最多。Pm為0.4時，標準偏差最小，為0.0358。因此，得出最優的Pc為0.9，Pm為0.4。

2 實際應用

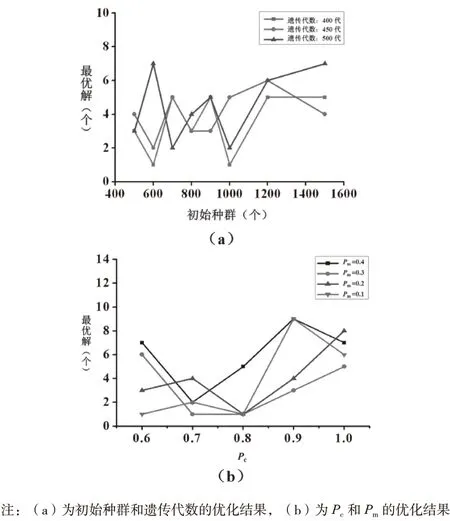
圖2 優化結果

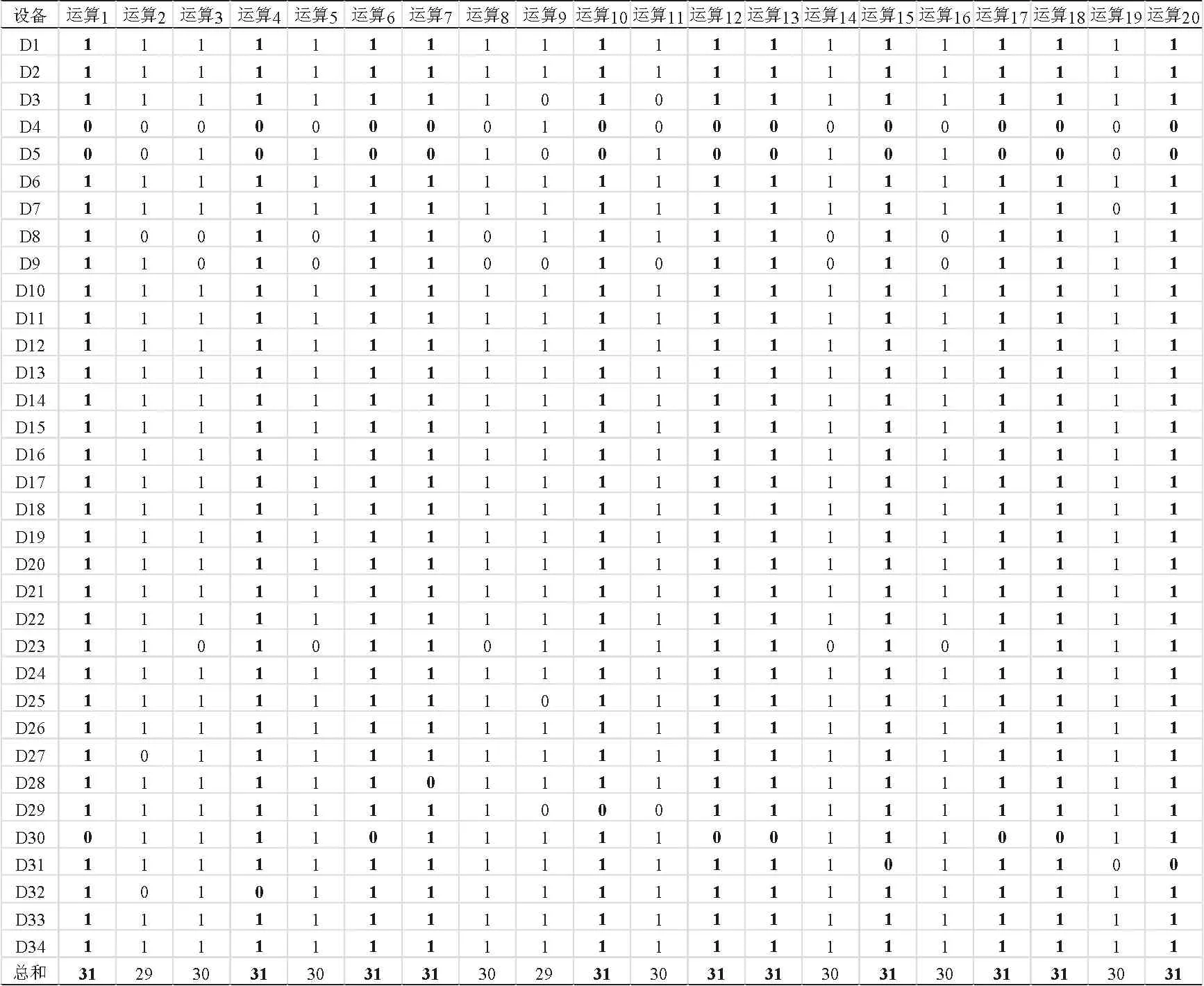
表2 醫療設備更新決策優化數據

應用最優解結果得到的最佳參數對初始種群進行運算，結果表明，當種群大小為600個、遺傳代數為500代、Pc為0.9、Pm為0.4時，最優解的最大數量為11個。所獲得的最優解見表2。表2中，運算結果為0，可能是因設備的更新因子較小或待更新設備型號高端導致購置價格較高，從而需從設備更新列表中排除。最優解為34臺輸入中的31臺，即34臺監護儀中有31臺監護儀可優先更新。進一步比較D1～D34的20次運算結果，最優解方案不包括消耗大量可用預算的高端型號監護儀（D4和D5），從而為其他購置價格低的低端型號提供了更多的更新機會。而D9編號的監護儀因更新因子相較于其他監護儀較小，在可用預算的約束下，該編號的監護儀也不在設備更新列表中。綜上所述，D4、D5和D9這3臺監護儀不在本年度設備更新計劃內。因此，根據提出的遺傳算法，在醫療設備更新可用預算比購置預算低20%的情況下，采用最優控制參數集，能得到醫療設備更新數量最大值的列表。需注意的是，在進行設備的更新決策時，需考慮同種設備的階梯配置，即種類相同、型號不同的設備單價差距較大。因此，在進行設備預算統計時，只有分清不同型號和來源的同種設備的單價，才能在不超出總體預算的前提下，進行遺傳算法的運算。

3 小結

因醫療設備更新決策的重要性，再考慮到醫療設備管理部門更新預算的限制，本研究建立了基于遺傳算法的醫療設備更新決策優化模型，并篩選出進入更新計劃的31臺設備。該模型突出了資金在醫療設備更新決策中的重要性，能夠盡可能地簡化操作并節約資金，指導醫療設備管理部門客觀地制訂預算采購計劃并進行設備更新決策管理。今后還可添加更多的設備來進一步自定義模型，修改條件和目標函數以便更好地展示醫療設備更新決策的特點。需說明的是，本模型是對之前研究[6]中基于故障樹分析法建立的設備更新模型的進一步改進和優化，所有的研究條件都是建立在該研究的模型上，如需使用本模型進行設備更新決策時需結合之前的模型，才能更好地做出醫療設備更新的決策。本研究采用遺傳算法來優化更新模型，也可使用其他算法，如禁忌搜索算法等，今后還可通過比較這些方法之間的差異來尋找更合適的優化方法，從而提高決策效率。