基于逆線性二次型控制活套優(yōu)化仿真設(shè)計

夏永彬 王海深 周廣成 郭維進 李偉 路統(tǒng)憲

(北京首鋼股份有限公司 河北唐山 064400)

1 前言

軋機間的活套在軋制中起著維持機架間秒流量平衡的作用，也保持帶鋼具有恒定張力的設(shè)定，然而活套的高度控制和張力控制兩者存在耦合作用，當(dāng)活套高度變化時，機架間張力會發(fā)生變化；機架間張力變化，角度也會發(fā)生變化，即活套控制是一個耦合系統(tǒng)[1-2]。機架間的套量由于在咬鋼速降、穩(wěn)態(tài)速度變化、帶鋼本體的干擾下，存在著一定的干擾，而張力由于軋制力的動態(tài)變化、軋機速度的干擾、帶鋼的問題，也會存在著一定的擾動控制。隨著對帶鋼質(zhì)量的要求增加，確保帶鋼間張力的穩(wěn)定，對帶鋼質(zhì)量的穩(wěn)定具有十分重要的作用[3]。

2 ILQ控制理論與反饋極點配置

ILQ控制理論是LQ二次型理論的基礎(chǔ)上逆向設(shè)計的，LQ設(shè)計流程圖如圖1所示。

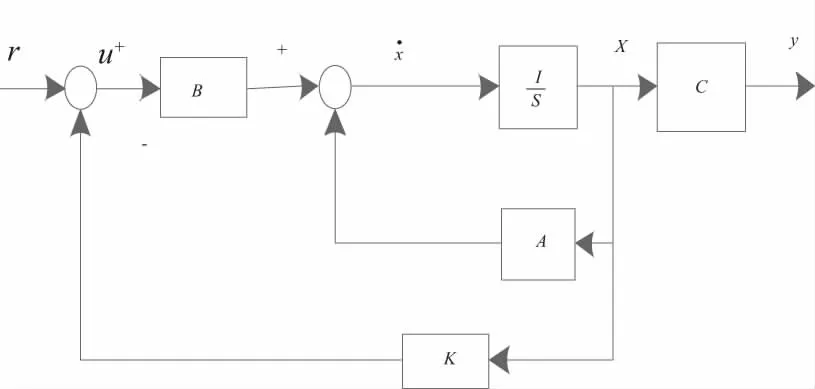
圖1 受控系統(tǒng)的控制模型

傳統(tǒng)受控系統(tǒng)狀態(tài)空間模型可以描述為：

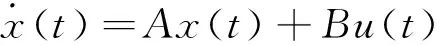
y(t)=Cx(t)

(1)

式中：x(t)—狀態(tài)向量；

u(t)—控制向量；

A、B和C—常數(shù)矩陣；

y(t)—輸出矩陣。

在上述系統(tǒng)中，設(shè)計最佳控制率u，實現(xiàn)上述系統(tǒng)的控制輸出y漸進設(shè)定r，此時的反饋矩陣采用的矩陣為K，此時的J考慮到系統(tǒng)狀態(tài)向量輸出最低，控制率輸出最小：

(2)

當(dāng)最優(yōu)控制存在且唯一，則

u=-Kx(t)=-R-1BTPx(t)

(3)

其中P是矩陣黎卡提代數(shù)方程的解

PA+ATP-PBR-1BTP+Q=0

(4)

進而可以通過黎卡提方程[K,P,E]=lqr(A,B,Q,R,N) 獲得反饋控制率K。

其中黎卡提方程可以得出最優(yōu)反饋控制K，設(shè)定的控制率u從而得出，采用該方式中Q和P加權(quán)矩陣往往需要大量經(jīng)驗實湊來獲得[4-5]。這在實際調(diào)試中往往不具有應(yīng)用條件，采用該方法進行Q和P的求解，往往只能應(yīng)用到仿真理論設(shè)計中。

3 活套ILQ逆線性二次型理論對活套控制器參數(shù)的優(yōu)化設(shè)計

3.1 活套的控制器模型參數(shù)

傳統(tǒng)活套控器模型的優(yōu)化，如下圖2所示。

yA=CAxA

(5)

假設(shè)系統(tǒng)在穩(wěn)態(tài)時：

(6)

上式中xs和us為穩(wěn)態(tài)值，前者為狀態(tài)向量，后者為控制率，得出活套模型控制器參數(shù)如下。

(7)

(8)

進而得出式子的控制率

(9)

通過上式中推到，可以得出在LQ基礎(chǔ)上進行兩級反饋的配置如圖2所示。

圖2 活套新模型控制功能圖

3.2 ILQ參數(shù)優(yōu)化設(shè)計

3.2.1 逆線性二次型的反饋極點配置

新模型的反饋矩陣需要考慮兩部分，包括反饋和積分增益。因此對上式所采用的ILQ理論進行期望極點配置，得到狀態(tài)反饋矩陣中KF和KI.其中KF和KI兩者之間具有一定線性關(guān)系，將[KFKI]進行線性變形，將該KI轉(zhuǎn)換為單位矩陣組成的表達形式[6]，如下式10所示。

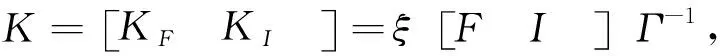
(10)

對于多輸入多輸出系統(tǒng)，極點配置所得到的反饋增益K往往不為一，上式表達出的反饋增益矩陣具有一定的可調(diào)節(jié)性。其中反饋增益KF求解可通過期望極點配置獲得，過程如下。

其中F=-GT-1，G為特征向量自由度配置矩陣，T為自由配置矩陣，可以通過計算得出。

設(shè)計方法如下[7]：

(1)獲取期望系統(tǒng)閉環(huán)極點{Si}。

(2)選擇G=[g1g2…gn-m]，其中G成為特征向量自由度配置矩陣。

當(dāng)選擇完G變量時，T=[t1t2…tn-m]，其中ti=(siI-A)-1Bgi

(3)其中ξ應(yīng)滿足ξ?λmax(E)(此處獲取ξ的下限)

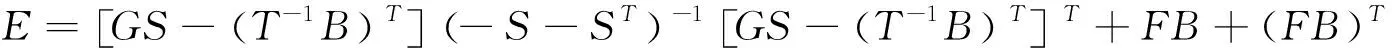
(4)構(gòu)造上式，最終可以得到反饋矩陣K

當(dāng)反饋矩陣K得出后，采用新控制器的活套模型響應(yīng)特性將由閉環(huán)系統(tǒng)矩陣AA-BAK的特征值來決定，當(dāng)ξ滿足下限值時，那么通過線性變化，可以將特征方程線性描述為：

其中V是需要大于一定的下限值的值，∑為對角矩陣形式。

當(dāng)ξ→∞，F(xiàn)的特征值λ(F)≈λ(A-BF)∪λ(-V-1∑V)

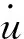
3.2.2 活套ILQ仿真與參數(shù)調(diào)節(jié)

對活套張力模型和高度模型進行建模[8]，得出活套模型的狀態(tài)矩陣方程：

上式中，E為帶鋼的楊氏模量(Mpa)，J為轉(zhuǎn)動慣量(Nms/rad)；f為前滑系數(shù)，F(xiàn)1為角度對力矩的影響系數(shù)，F(xiàn)2為角速度對套量影響系數(shù)(m/rad)，F(xiàn)3為張力對力矩的影響系數(shù)(Nm/Mpa)，BT為液壓缸流量增益系數(shù)，gl為角速度到角度轉(zhuǎn)換系數(shù)。

通過閉環(huán)極點來推到反饋增益系數(shù)的過程：

A-BF=A-B(KFA+KIC)=(I-BKF)A-BKIC

假設(shè)閉環(huán)極點的位置期望和張力期望為wTC、wHC

則將行列式變成矩陣的形式，通過系數(shù)相同法可以得出相應(yīng)的狀態(tài)

采用多項式的系數(shù)相等法進行可以得出以下參數(shù)

通過上式描述可以得到系統(tǒng)的ILQ的控制框圖，如圖3所示。

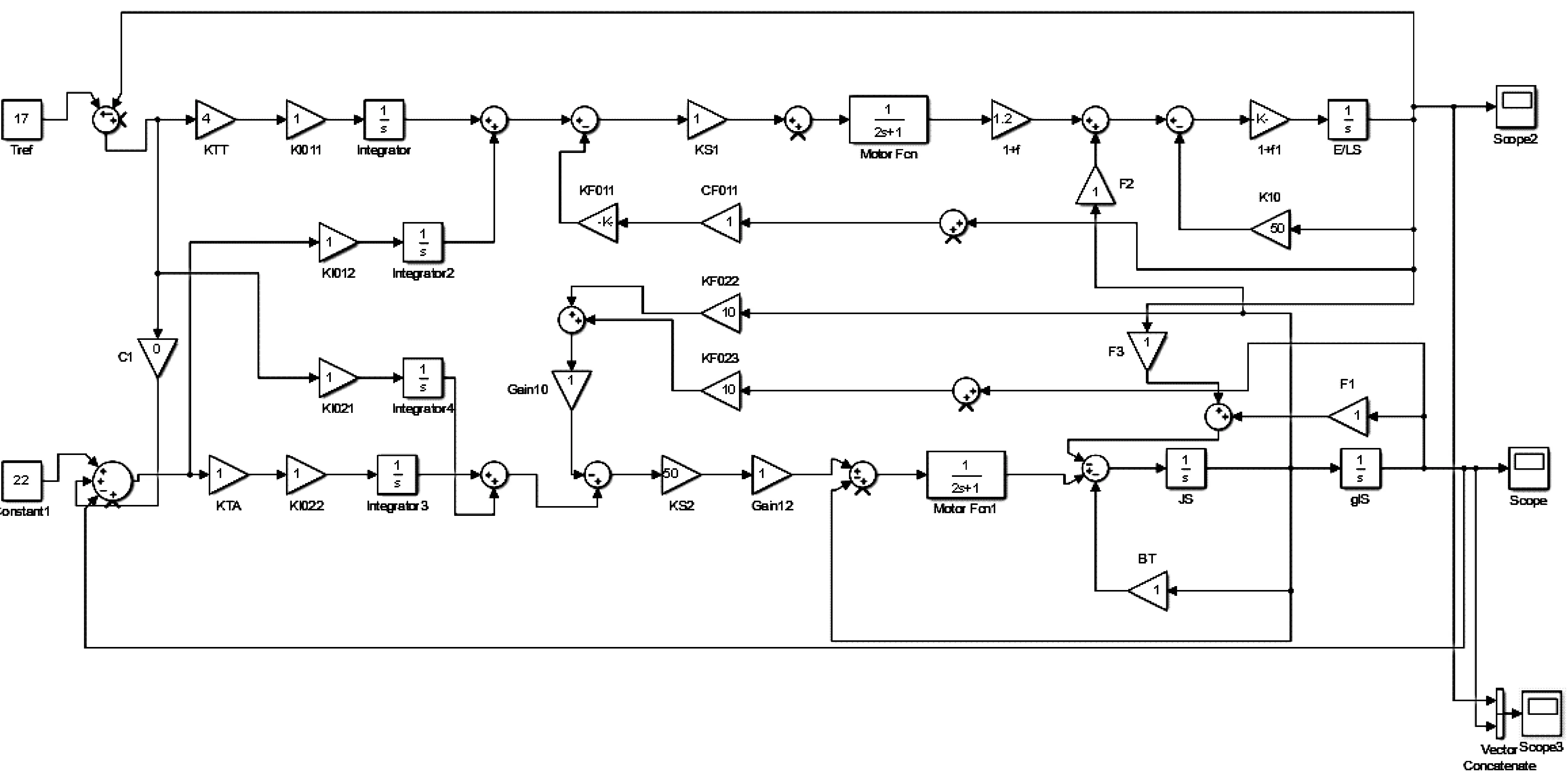
圖3 活套新模型ILQ控制功能圖

通過ILQ理論推導(dǎo)，活套模型是在LQ控制基礎(chǔ)上改進模型而設(shè)計的，其中上式中的Ks1表示上式(10)中的單位設(shè)定參數(shù)，Ks2可調(diào)增益系數(shù)相當(dāng)于式(10)中的增益系數(shù)ξ；設(shè)計反饋增益系數(shù)時，反饋增益系數(shù)KF和KI之間需滿足一定線性關(guān)系；當(dāng)ξ→∞，反饋增益的特征值將趨近于特征極點wHC、wTC，積分增益矩陣的特征值此時將趨近于無窮。

4 實際仿真參數(shù)設(shè)計

結(jié)合圖3中的仿真設(shè)計，調(diào)節(jié)參數(shù)使得仿真輸出圖4(a)中在此基礎(chǔ)上進行參數(shù)調(diào)節(jié)，設(shè)計張力輸出17Mbar，角度設(shè)定輸出為22°，與實際生產(chǎn)設(shè)定相符。

(1)圖4(b)仿真設(shè)計中，當(dāng)模型一定的時候，適當(dāng)增加張力環(huán)可調(diào)增益系數(shù)Ks1，可以使張力響應(yīng)增加，活套角度響應(yīng)下降，調(diào)節(jié)該參數(shù)使得角度和張力響應(yīng)過程趨勢效果相反；

圖4 單獨增大參數(shù)Ks1

(2)圖5(a)所示，適當(dāng)增大Ks2=40，系統(tǒng)的角度響應(yīng)速度和張力響應(yīng)速度增加，具有良好的參數(shù)可調(diào)節(jié)性，該參數(shù)的調(diào)節(jié)區(qū)間范圍較大。然而該參數(shù)不能太大，參數(shù)太大容易使得可投入的條件越來越苛刻，圖5(b)中Ks2=80，響應(yīng)初始階段不具備條件。

圖5 單獨增大參數(shù)Ks2

(3)經(jīng)過參數(shù)優(yōu)化后，在擾動測試中，圖6(a)中當(dāng)對張力進行擾動時，角度會進行偏轉(zhuǎn)以實現(xiàn)張力恢復(fù)到設(shè)定值，而在圖6(b)中僅對角度進行擾動時，張力擾動變換具有較小干擾，這樣會讓在軋制中更加良好的保證帶鋼的質(zhì)量。

圖6 分別給張力和角度進行幅值干擾

5 應(yīng)用效果

本次設(shè)計在結(jié)合著軋制屈服強度較大的難軋規(guī)格酸洗板Q420-P，在進行參數(shù)優(yōu)化后，得到F6活套響應(yīng)過程如圖7所示：

圖7 投入ILQ設(shè)計的角度效果

在軋制過程，當(dāng)角度在設(shè)定值穩(wěn)定后程序自動切換成ILQ逆線性二次型控制中，在原參數(shù)基礎(chǔ)，適當(dāng)減小Ks1和增大Ks2參數(shù)，可以保證帶鋼在軋制中的穩(wěn)定性。當(dāng)張力出現(xiàn)擾動時，角度的變化明顯，目的實現(xiàn)快速張力穩(wěn)定，而角度擾動時，張力變化比較平穩(wěn)，和理論仿真效果一致。

6 結(jié)論

本次設(shè)計在帶鋼建立張力到張力連軋階段，提出了ILQ逆線性二次型優(yōu)化控制設(shè)計，在活套進入張力連軋階段，通過理論設(shè)計，適當(dāng)調(diào)節(jié)參數(shù)ILQ逆線性二次型中的增益參數(shù)Ks1和Ks2，有效保持當(dāng)出現(xiàn)張力擾動時，角度響應(yīng)具有快速性，維持帶鋼張力穩(wěn)定，當(dāng)角度出現(xiàn)擾動時，張力具有一定的魯棒性，保持帶鋼張力的穩(wěn)定，仿真和實踐都表明基于ILQ控制理論的活套控制效果良好，保證了生產(chǎn)的穩(wěn)定性和質(zhì)量的可靠性。