多層非均勻徑向復合儲層壓力動態特征
高 敏,段 蕾,史文洋,顏家偉,陸科杰
(1.中國石油股份有限公司長慶油田分公司第四采油廠,寧夏銀川 750006;2.中國石油大學(北京)油氣資源與探測國家重點實驗室,北京 102249;3.中國石油股份有限公司長慶油田分公司第三采油廠,寧夏銀川 750006;4.中海油能源發展股份有限公司工程技術分公司,天津 300452)
隨著石油勘探開發理論與技術的發展,越來越多的復雜油氣儲層被發現并進行商業開采。儲層的描述表征以及生產過程中的儲層再認識一直是礦場比較關心的問題。在非均質儲層滲流的刻畫方面,層狀油藏模型和復合油藏模型是最常用的兩種經典模型。Gao[1]針對多層油藏首次提出了存在層間越流的半透壁滲流模型,Bourdet[2]建立了經典的無越流層狀儲層壓力模型。文獻[3-9]研究了多層合采油氣藏的儲層壓力和滲流特征,建立了考慮層間越流和無層間越流的壓力響應模型,奠定和發展了多層油藏滲流與試井方法理論。文獻[10-15]對多層油氣藏滲流模型進行了系統的綜述,總結對比了考慮復合特征的多層儲層滲流模型的求解方法以及內外邊界條件等,最后給出了多層徑向復合模型壓力解的結構和求解方法。
現存的多層徑向復合滲流模型中,只針對較少層數(2~3層)的模型進行各層復合半徑不相等的處理。嚴格意義上說,缺少真正的多層非均勻徑向復合儲層滲流模型。為了明確縱向非均勻復合儲層的壓力響應特征,分析非均勻復合半徑對壓力響應的影響規律,本文建立了考慮各類非均勻復合半分布的多層儲層壓力響應模型,進一步完善和補充了多層復合儲層滲流理論。
1 模型的建立與求解
1.1 物理模型
縱向非均勻徑向復合模型如圖1所示,假設儲層為n層,各層均為水平等厚的儲層;第j(j=1,…,n)層的流體黏度、儲層綜合壓縮系數、厚度分別為μj、Ctj、hj;第j層內區滲透率、孔隙度、外邊界分別為k1j、Φ1j、rcj,第j層外區滲透率、孔隙度、外邊界分別為k2j、Φ2j、re;生產井位于儲層中心,以定產q進行生產;開井前儲層壓力處處相等,儲層內充滿微可壓縮流體;開井后各層流體滿足達西定律向井底徑向流動,且層間無越流。

圖1 縱向非均勻徑向復合模型示意圖
以井軸為中心,各層流體向井底流動時各層儲層內壓力p的分布滿足下述定解問題。
(1)
pij|t=0=pr
(2)
(3)
p1j|rD=1=pw
(4)
(5)
p1j|r=rcj=p2j|r=rcj
(6)
p2j|r→∞=pr
(7)
1.2 數學模型
定義無量綱變量:
rD=r/rw
(8)
(9)
(10)
(11)
pijD=2π(kh/μ)a(pr-pij)/q
(12)
χij=(kh/μ)ij/(kh/μ)a
(13)
ωij=(ΦCth)ij/(ΦCth)a
(14)
Mj=(kh/μ)1j/(kh/μ)2j
(15)
Dj=(ΦCth)1j/(ΦCth)2j
(16)
式中χ——流動系數比,無量綱;
ω——儲容系數比,無量綱;
M——滲透比,無量綱;
D——儲能比,無量綱。
拉氏空間下對應的由無量綱滲流方程和邊界條件構成的數學模型為:
(17)
式中u——拉氏空間變量;

1.3 模型求解
內區滲流方程解可用Bessel函數表示:
(18)
式中A——待求系數,無量綱;
Ia——a階第一類修正Bessel函數,無量綱;

B——待求系數,無量綱;
Ka——a階第二類修正Bessel函數,無量綱。
外區為無限大邊界,滲流方程解為:
(19)

式(18)和(19)中一共有3n個未知系數,根據內邊界的1個產量方程、n-1個壓力方程,層交界面n個流量連續方程、n個壓力連續方程,得到3n×3n線性方程組:
(20)
式(20)中,aj=χjσ1I1(σ1),bj=-χjσ1K1(σ1),cj=I0(σ1),dj=K0(σ1),ej=σ1I1(σ1rcDj),fj=-σ1K1(σ1rcDj),gj=σ2K1(σ2rcDj)/Mj,hj=I0(σ1rcDj),mj=K0(σ1rcDj),oj=-K0(σ2rcDj)。

(21)
利用Shetfesh數值反演方法得到實空間下無量綱井底壓力的解pwD。
2 模型典型曲線特征
以n=10為例,圖2為模型參數弱化后的井底壓力和壓力導數曲線。模型的參數弱化說明非均勻復合模型是縱向均質復合模型的泛化,縱向非均勻復合模型相比于單層復合模型具有更廣的適用范圍。從壓力和壓力導數典型曲線上可以看出縱向非均勻復合儲層存在3個明顯的流動特征。

圖2 縱向非均勻復合模型典型曲線
(1)內區徑向流階段:在縱向均質的條件下,內區徑向流階段的壓力導數l為0.5;在縱向非均質的條件下,內區徑向流階段的壓力導數仍為一段水平線,壓力導數值l=0.5/n。
(2)過渡流階段:由于外區儲層物性變差(M=D>1),因此壓力導數出現上升。當外區儲層物性遠遠差于內區儲層物性時(M=D=100),壓力和壓力導數曲線出現類似封閉邊界的特征,壓力和壓力導數斜率m=1。
(3)外區徑向流階段:當壓力傳播到外區更遠的儲層時,外區流體徑向地流進內區,流動表現為徑向流動階段,壓力導數值L=M·l。
3 敏感性分析
3.1 層數
圖3揭示了縱向非均勻復合模型中層數n對井底壓力響應的影響規律。如圖3所示:n=2時,取rcD=100,內區徑向流階段的壓力導數值l1=0.25;n=5時,取rcD=200,內區徑向流階段的壓力導數值l2=0.1;n=10時,取rcD=400,內區徑向流階段的壓力導數值l3=0.05。即內區徑向流階段的壓力導數值l=0.5/n。

圖3 層數敏感性分析
3.2 非均勻復合半徑
為了分析多層非均勻復合半徑對井底壓力響應的影響,設計了兩類縱向非均勻內區半徑。第一類是直線類內區半徑,用來刻畫斷層、地壘、地塹式復合儲層[12-13];第二類是雙曲類內區半徑,用來模擬碳酸鹽巖填充溶洞或者砂巖透鏡狀、塊狀巖性復合儲層[20-23]。
3.2.1 直線類復合半徑
圖4顯示了2種直線傾覆內區半徑與3個均勻內區半徑的壓力響應曲線。圖中所示傾覆類內區半徑具有3種性質。①對稱性:兩種直線傾覆類內區半徑對應的壓力響應曲線完全重合;②有界性:直線傾覆類內區半徑壓力響應曲線介于最小內區半徑和最大內區半徑對應的壓力響應曲線之間;③中值性:存在一個內區中值半徑的壓力響應曲線與實際直線傾覆類內區壓力響應曲線完全重合,且內區中值半徑不等于內區均值半徑。內區中值半徑的取值遵守等效滲流空間法則:非均勻復合儲層的滲流空間是復雜的,可以用一個規則的滲流空間來替代它,使兩者具有相同的壓力響應特征。等效滲流空間可以解釋試井多解性:無論多么復雜的儲層,總能找到一個或多個等效滲流空間。由于均值半徑不一定等于中值半徑,因此,慎用均值半徑處理縱向非均勻徑向復合類儲層。
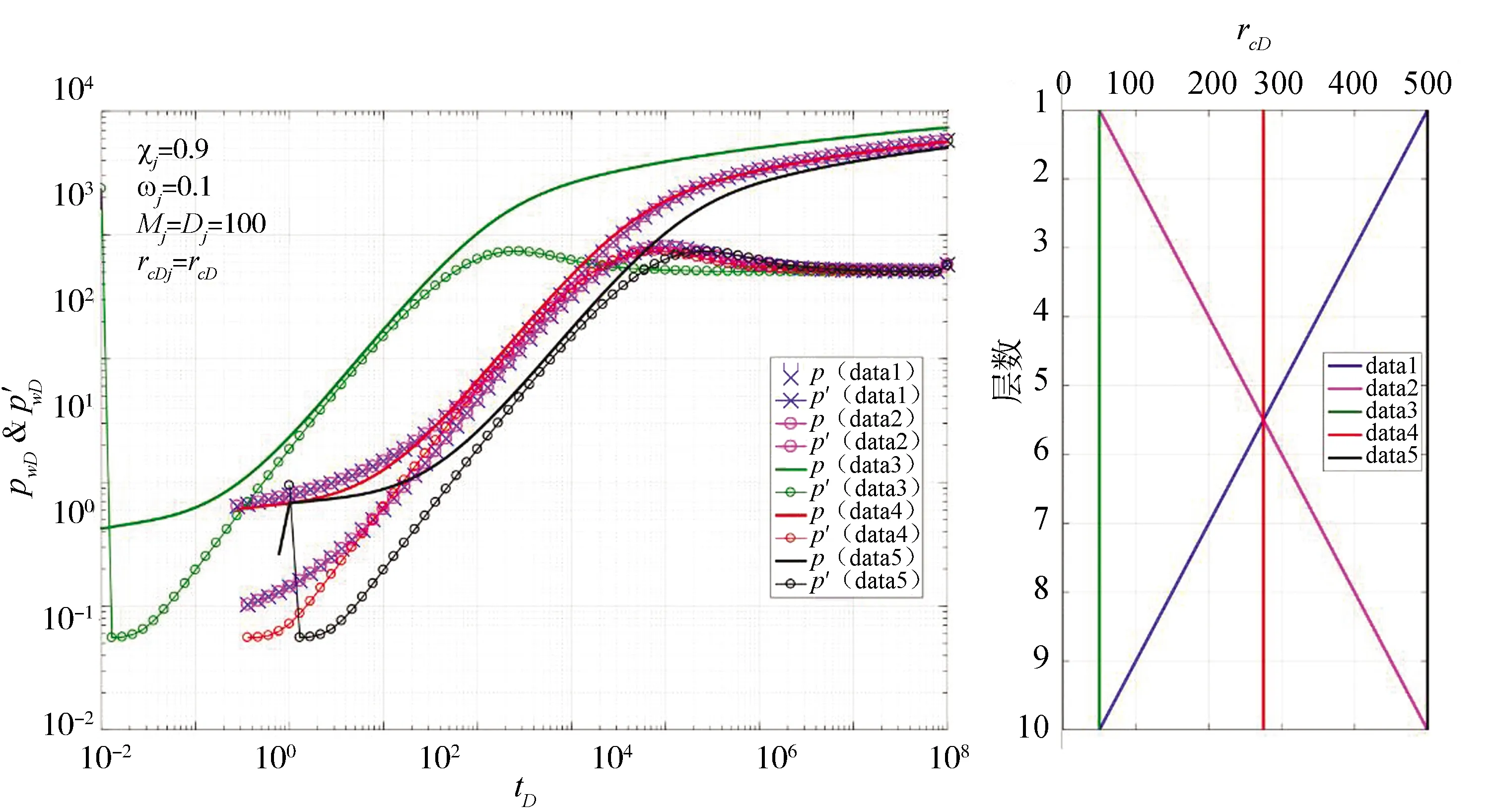
圖4 直線類內區半徑敏感性分析
3.2.2 雙曲類復合半徑
圖5表示拋物線型內區前緣對壓力響應的影響規律:參與徑向復合滲流的層數逐漸減少,內區徑向流階段的壓力導數值按照l=0.5/n的規律逐漸增大;根據等效滲流體積的概念,內區中值半徑逐漸減小,過渡流出現的時間靠前。圖5中①和②內區前緣具有相同的壓力響應曲線,說明兩者具有相同的等效滲流體積。如果儲層厚度很大,或內區體積不是很大,則通過井底壓力響應曲線難以識別內區復合體積的縱向位置,如圖6所示。

圖5 拋物線型內區半徑敏感性分析

圖6 內區體積縱向位置敏感性分析
4 實例分析
圖7表示B2井于2006年9月進行的一次壓力恢復的測試結果。結合B2井的儲層構造來看,“三邊封閉+一邊定壓”矩形外邊界模型是最符合B2井實際儲層特征的[21];如果不結合儲層特征,僅針對B2井的壓恢數據就有5種外邊界解釋模型能較好地擬合,其中3個矩形邊界模型解釋的最近封閉邊界分別為101 m、115 m、140 m,2個徑向復合得到的內區半徑值分別為120 m、122 m(表1)。

表1 各類擬合模型的邊界類型及參數

圖7 B2井雙對數曲線及各類邊界擬合對比圖
3類矩形邊界得到的最近封閉邊界平均值為118.67 m,與2個復合半徑都十分接近。根據等效滲流體積概念可以認為:B2井對應的等效滲流體為半徑約為120 m的圓柱體,滲流范圍超過120 m將會收到儲層外邊界的干擾和影響。等效滲流體積的概念可以用來簡化并解釋實際復雜儲層,但是容易丟失真實和精細的儲層特征。利用等效滲流體積可以解釋試井的多解性,但是試井的多解性問題需要結合地質資料和現場認知消除。
5 結論
(1)縱向非均勻徑向復合滲流儲層存在3個流動階段:內區徑向流、過渡流、外區徑向流。內區徑向流階段的壓力導數值l與參與徑向復合滲流的層數n有關:l=0.5/n;過渡流出現的時間與內區中值半徑有關;外區徑向流的壓力導數值L與內區流度比M有關:L=M·l。
(2)縱向非均勻徑向復合半徑對壓力響應的影響規律具有:①對稱性,具有對稱的兩個非均勻徑向復合儲層具有相同的壓力響應;②有界性,非均勻徑向復合儲層壓力響應曲線位于最小復合半徑和最大復合半徑對應的壓力響應曲線之間;③中值性,存在一個縱向均勻的內區半徑,其對應的壓力響應與非均勻徑向復合半徑對應的井底壓力響應相同。
(3)內區中值半徑代替非均勻徑向復合半徑引起的壓力響應誤差遠小于均值半徑代替非均勻徑向復合半徑引起的誤差,中值半徑可以根據等效滲流體積法則得到;內區均值半徑不一定等于內區中值半徑,慎用均值半徑替代縱向非均勻復合半徑。
(4)等效滲流體積法則可以解釋試井的多解性。可以用等效中值半徑處理縱向非均勻類復雜儲層,解釋其井底壓力響應行為,但是等效中值半徑的處理方法不能夠準確精細地描述復雜儲層的局部特征。

