一種基于異地處理的抵近探測雷達系統

馬紅星

(海裝上海局駐合肥地區軍事代表室，安徽合肥 230088)

0 引言

由于地球曲率的影響，為探測低空突防目標，需要同時實現雷達架高和雷達功率孔徑的增加。現有的提升低空目標預警時間的主要手段有利用更大的載機平臺，加裝更大功率孔徑積的雷達系統來提升遠距離的預警能力。但大型的預警平臺同樣也面臨滯空時間和戰場生存的挑戰[1-3]。此外，大型系統平臺的復雜性以幾何級數增加，并帶來體積、重量、散熱、維修、使用和保障等多方面的諸多問題。而且，通過增加雷達功率或孔徑來提升雷達的探測威力往往也是事倍功半。根據雷達方程，為使雷達威力提升為原來的2倍，需要增加雷達功率孔徑積至原來的16倍[4]。因而，探究一種可在有限功率孔徑積下實現更遠距離目標預警的新體制雷達，這對于預警體系的構建具有重要意義。

文章提出了一種增加轉發站來實現定向遠距離目標探測的新體制雷達。該雷達由發射站、轉發站和接收站三部分組成。雷達工作時，發射站采用MIMO雷達[5-7]的工作方式，發射正交波形信號；轉發站采用抵近目標的方式，進行目標回波信號的探測，以獲取滿足一定信噪比要求的信號，為避免與目標回波信號的相互干擾，轉發站對接收到的信號進行錯頻回傳；接收站接收回傳信號，完成等效發射波束形成并進行信號處理，實現目標探測。該雷達的發射波束為正交波形，因而利用單通道接收的回波信號即可實現等效發射波束形成。轉發站采用單個通道對目標回波進行接收時，僅需要對回波信號進行放大和錯頻回傳，避免了接收過程中由于轉發站接收天線指向和多通道信號回傳過程中的相互干擾問題。這使得轉發站功能簡單，僅需要對接收到的信號進行錯頻回傳，其在工作過程中可以不受探測信號的波形、帶寬等參數的影響，損失或被截獲后安全風險較小。同時，簡單的功能結構也使得轉發站具有常規雷達設備難以獲取的小體積和低功耗等特點，為其靈活部署實現抵近探測創造了必要的基礎條件。該雷達實現了在不改變發射站功率孔徑積的前提下，通過將轉發站抵近目標的方式，實現遠距離目標的探測，為提升雷達遠距離預警能力提供了一種可供參考的思路。

1 基本原理

該體制雷達由發射站、轉發站和接收站三部分組成，原理示意圖如圖1所示。發射站發射正交探測波形信號；信號在空間中進行輻射，經目標散射后的回波信號被轉發站接收，轉發站對接收到的回波信號進行錯頻回傳，接收站接收回傳信號，進行等效發射波束形成并完成回傳信號的處理，實現目標探測。

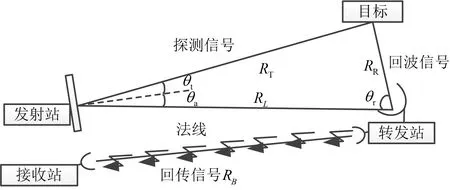
圖1 雷達原理示意圖

1.1 信號模型

考慮發射陣面是一個M個陣元組成的線陣，陣元間距為d，如圖2所示。假定相鄰陣元之間的頻率間隔為Δf，第m個陣元發射信號的頻率為fm，有

fm=f0+am·Δf

(1)

式中，am∈{0,1,2,…,M-1}為發射陣元的序號，f0為雷達工作頻率。則第m個陣元的發射信號可以表示為

sm(t)=Re{xm(t)exp(j2πfmt)}

(2)

式中，xm(t)為第m個發射信號的復包絡。第m個陣元的發射信號到達空間中某點的信號可以表示為

sm(t-τm)=Re{xm(t-τm)·

exp(j2πfm(t-τm))}

(3)

式中，τm為第m個發射陣元到該點的傳播時延。

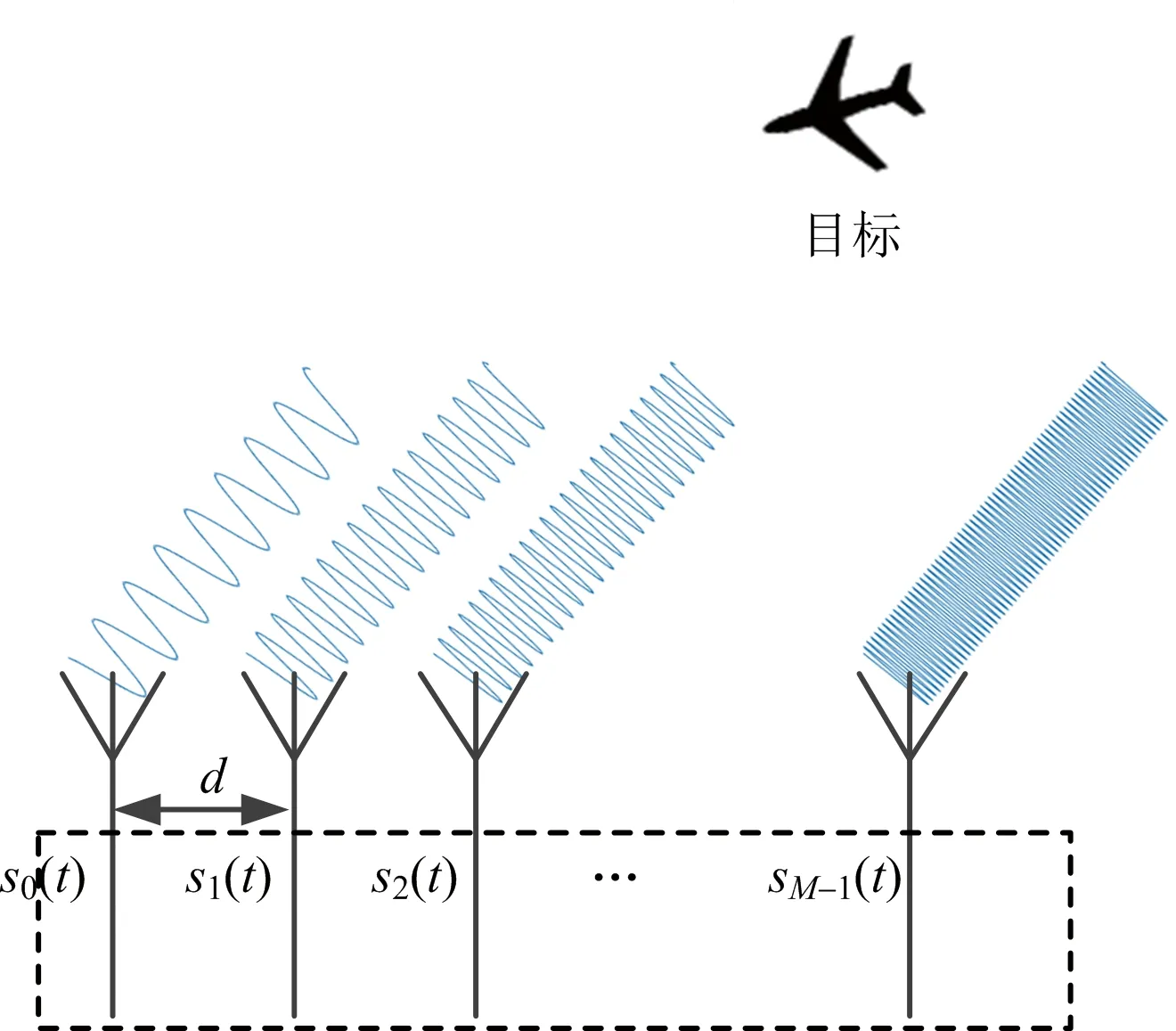
圖2 發射站原理示意圖

假定在p點有一個目標，其角度位置矢量為Θ，運動速度為v，則轉發站接收陣元接收到的信號可表示為

rr(t,Θp,vp)=

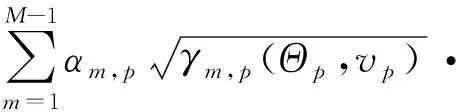
xm[γm,p(Θp,vp)(t-τm,p)]·

exp(j2π(f0+am·Δf)·

γm,p(Θp,vp)(t-τm,p))+n1(t)

(4)

式中，n1(t)為轉發站接收到的環境噪聲，τm,p為發射站第m個陣元經目標后到達轉發站接收天線的時延，αm,p為發射站第m個發射陣元經目標p散射后到轉發站接收陣元的衰減因子，γm,p(Θp，vp)為目標運動產生的拉伸因子，且

γm,p(Θp,vp)=1+fm,p(Θp,vp)/f0

(5)

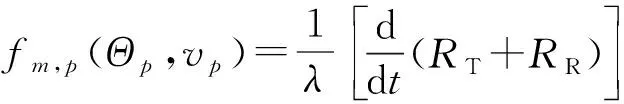
由于發射站發射的探測信號采用了正交波形信號，目標回波信號中包含了目標相對于發射站的相對方位信息，通過單個接收通道獲取的目標回波信號即可實現等效發射波束形成。基于此，轉發站基于單個接收通道獲取目標回波信號，并將接收到的信號進行錯頻回傳。錯頻傳輸的目的主要是為了防止探測信號和回傳信號相互之間的干擾。轉發站的工作原理如圖3所示，轉發站接收天線接收目標回波信號后經限幅低噪放，進行混頻、濾波放大處理后經回傳天線傳輸至接收站。

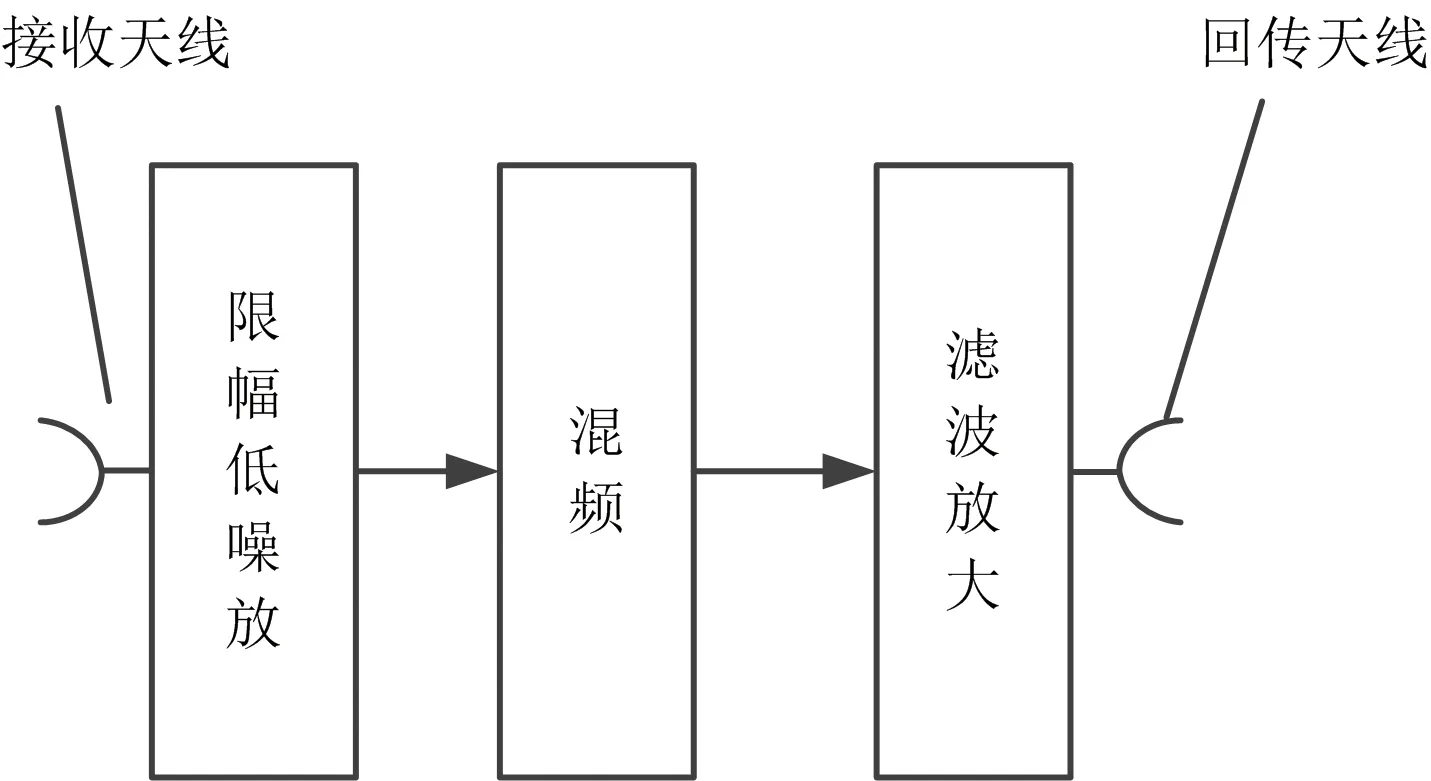
圖3 雷達轉發站工作原理圖

不考慮雷達轉發站內部對信號傳輸的影響，轉發站對信號的影響僅為放大和頻率調制。其輸出端的表達式可以表示為

rr′(t,Θp,vp)=A·rr(t,Θp,vp)·

exp(j2π(f1-f0)t)

(6)

式中，A為信號增強倍數，fB為回傳鏈路的工作頻率。接收站接收到的信號為

r(t,Θp,vp)=

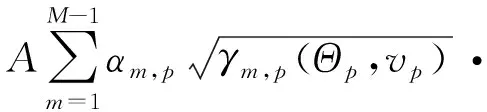
xm[γm,p(Θp,vp)(γB(ΘB,vB)(t-τB)-τm,p,d)]·

exp(j2π(f0+am·Δf)·

γm,p(Θp,vp)(γB(ΘB,vB)(t-τB)-τm,p,d))·

exp(j2π(f1-f0)γB(ΘB,vB)(t-τB))+

An1(t)+n2(t)

(7)

式中，τB為轉發站到接收站的傳播時延，γB(ΘB，vB)=1+fd/(fB-f0)為轉發站和接收站相對運動產生的拉伸因子，fd為轉發站和接收站相對移動產生的多普勒頻移。

1.2 模糊函數

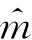
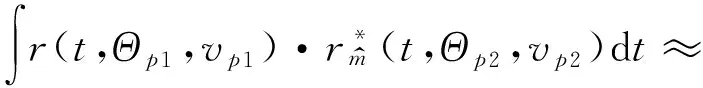
fmγm(γB1τB1+τm,p1,d))]·

(8)

其中，衰減因子為

相位函數為

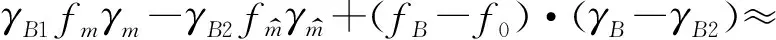
式中，Δfd1為目標相對于發射站和轉發站的移動引起的多普勒頻移，Δfd2為轉發站與接收站的相對運動引起的多普勒頻移。

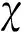
(9)

其中，exp[-j2π(fB-f0)(γB2τB2-γB1τB1)]為一個模為1的常數，導向矢量

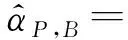
exp[j2π(fM-1+fd1)(τB+τM-1,p,d)]]T

(10)

協方差函數

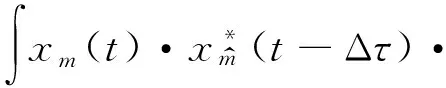
exp(j2π(ΔamΔf+Δfd)t)dt

(11)

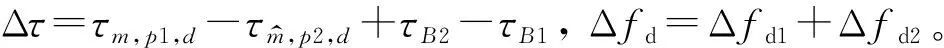
1.3 空間模型

從圖1可知發射站、目標、轉發站和接收站的空間關系。其中，發射站、轉發站和接收站的位置可通過定位設備測定，相應地，可求得發射站與轉發站之間的距離RL、轉發站與接收站之間的距離RB、轉發站與發射陣面法線的夾角θa。發射站、目標和轉發站三者之間滿足三角關系：

(12)

式中，RT為發射站到目標的距離，RR為轉發站到目標的距離。此外，通過等效發射波束形成可以求解得到目標相對于發射站法線的夾角θt，信號處理可以計算得到信號從發射站經目標、轉發站到接收站的總時延τall。

τall=(RT+RR+RB)/c+τp

(13)

式中，τp為信號在轉發站內所經過的時間，即電磁波從轉發站的接收天線到回傳天線的傳輸時間，該值為固定值，可以通過時延測量方法測得并從總時延中減去。因而，根據三角關系，目標相對于發射站的距離為

(14)

式中，τw=τall-τp。

至此，求解得到了目標相對于發射站的角度θt和距離RT，實現目標的定位。

2 威力分析

雷達威力是雷達最為重要的指標之一，對該體制雷達的威力進行分析具有重要意義，其中雷達孔徑和功率是設計過程中主要的變量。假定該雷達發射站的功率為P，發射增益為GT，目標的RCS為σ。雷達接收功率為

(15)

式中，Az為轉發站接收陣面的有效孔徑，AR為接收站接收陣面的有效孔徑，Gzg為轉發站的功率放大增益，Gzt為回傳天線的增益。

不同于常規雷達，該體制雷達在轉發站和接收站的接收過程中都會引入噪聲，噪聲功率密度可表示為

(16)

式中，Tsz為轉發站接收端的噪聲溫度，Tsr為接收站接收端的噪聲溫度。對于寬度為τ的單個脈沖，當采用匹配濾波器時，接收站的接收機輸出信噪比為

(17)

這里僅對比引入轉發站后對于威力的影響，因此可忽略其他諸如積累脈沖、信號傳輸和處理等因素的影響。

常規雷達接收機的信噪比為

(18)

由于該體制雷達的變量較多，為了更為形象地對比該體制雷達與傳統雷達的威力，基于真實應用場景對其進行了合理假設。

首先，雷達的孔徑通常在幾平方米到幾十平方米之間，而轉發站為了實現小型化其孔徑通常要遠小于發射站的孔徑，不妨假定轉發站的接收天線的孔徑為原雷達的1/10，即Az=A/10。

其次，考慮到大型雷達的探測威力通常為數百乃至上千公里，而轉發站抵近目標進行工作。假定RR=RT/20。

再次，雷達的噪聲溫度會隨著接收機的不同而不同，但差異較小，因而假定Tsz=Tsr=Ts。

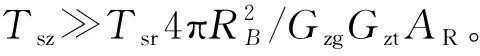
基于上述假設，求解可得RT=2.515R，即在該假設條件下，通過引入轉發站可以將雷達的威力提升為原來的2.515倍。同時，通過更改轉發站接收陣面的有效孔徑或轉發站與目標的距離，可以進一步優化雷達在特定方向上的探測威力。

3 仿真試驗

為了進一步對該體制雷達系統的可行性進行探究，文章對其模糊函數開展了相應的數值仿真分析。假定雷達發射站的工作頻率為3 GHz，發射陣面為16個陣元組成的線陣，陣元間距d=λ/2，回傳鏈路工作頻率為2 GHz。假定發射脈沖為脈沖寬度Te為10 μs的線性調頻(LFM)信號波形[8-10]，信號帶寬B為0.4 MHz，不同陣元間信號的中心頻點的頻差Δf為0.4 MHz。

根據公式(12)可得，該體制雷達系統的模糊函數表達式不僅包含了探測鏈路的參數因子，同時也包含了回傳鏈路的回傳頻率fB、時延τB和多普勒頻移fd2等參數。即該雷達系統的模糊函數也受回傳鏈路的影響。為了對雷達系統的模糊函數進行更為直觀的分析，對參數變量進行了限制，假定轉發站和接收站的位置相對固定。對雷達的模糊函數圖進行繪制，如圖4所示。

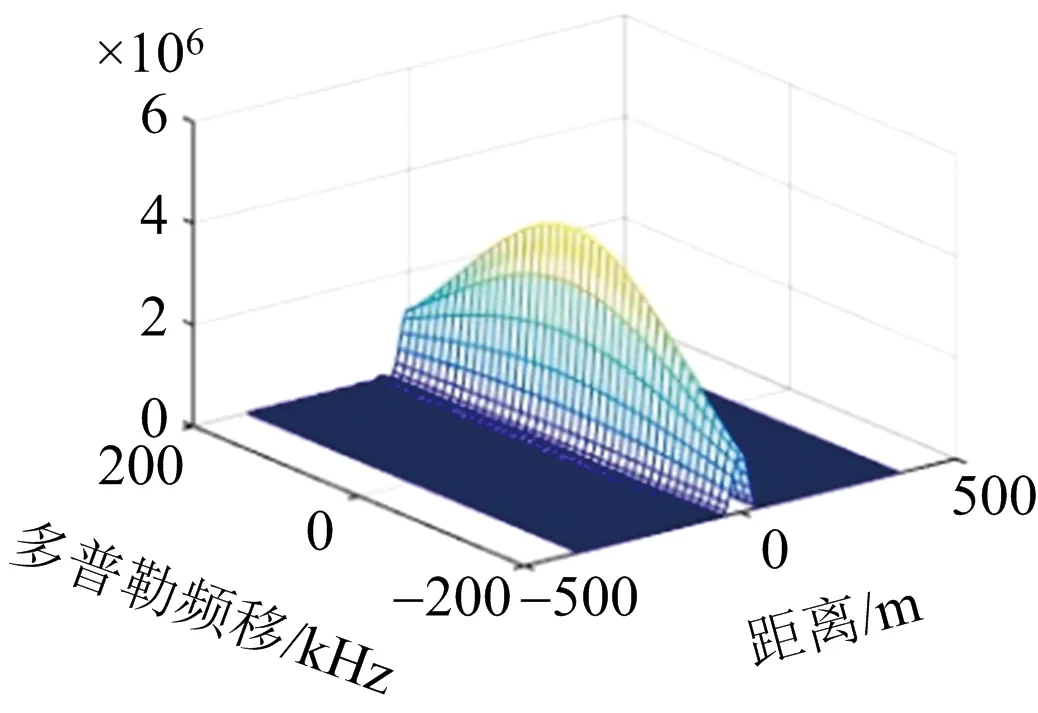
(a) 距離-多普勒模糊函數圖

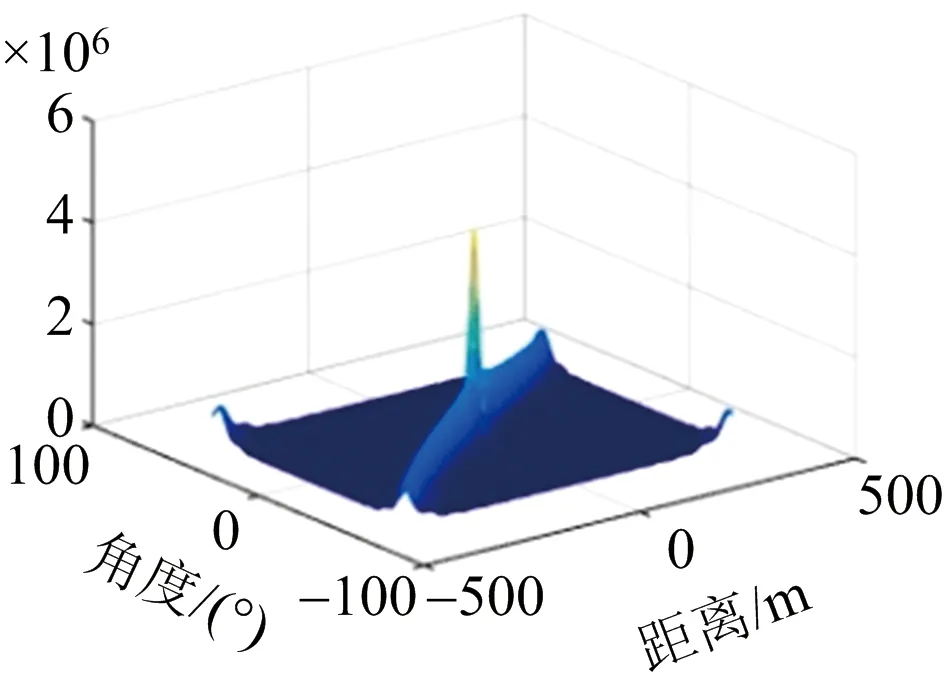
(b) 距離-角度模糊函數圖

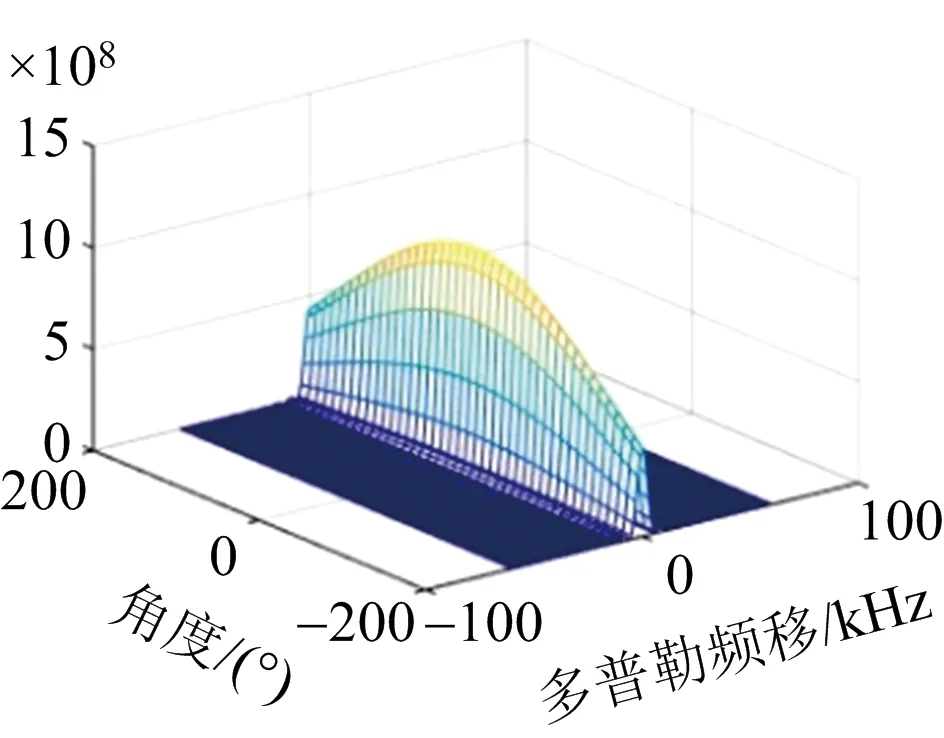
(c) 多普勒-角度模糊函數圖圖4 雷達系統的模糊函數圖

圖4(a)為距離-多普勒模糊函數圖，該模糊圖的形狀為正橢圓形，距離速度之間的相互耦合較小，能夠較好地實現對目標的分辨。圖4(b)為距離-角度模糊函數圖，該距離-角度模糊圖呈現斜刀刃狀，說明距離和角度兩者之間存在較大的耦合度，其中一個的變化會影響到另一個的變化。圖4(c)為角度-多普勒模糊函數圖，其形狀與距離-多普勒模糊函數圖相似，也為正橢圓形，這說明目標角度和速度之間耦合性較小，具有較好的分辨率。

與典型的雷達系統不同，該體制雷達轉發站接收回波信號后并不作計算處理，而是將接收到的回波信號進行錯頻回傳，由接收站完成數據處理。在實際應用場景中，轉發站通常根據需要會部署于無人機等移動平臺上進行抵近探測。為考察回傳鏈路對模糊函數的影響，文章對轉發站和接收站之間存在相對移動時的場景開展了數值仿真。圖5所示為轉發站與接收站之間存在相對運動時的模糊函數圖。實際場景中，轉發站和接收站兩者之間并不會存在如此之大的相對速度，這里只是為仿真兩者之間的相對移動對于雷達系統模糊函數的影響。對比圖5和圖4中對應的模糊函數圖可以看出，模糊函數圖僅在多普勒維上發生了移動，其形狀并沒有發生明顯變化。

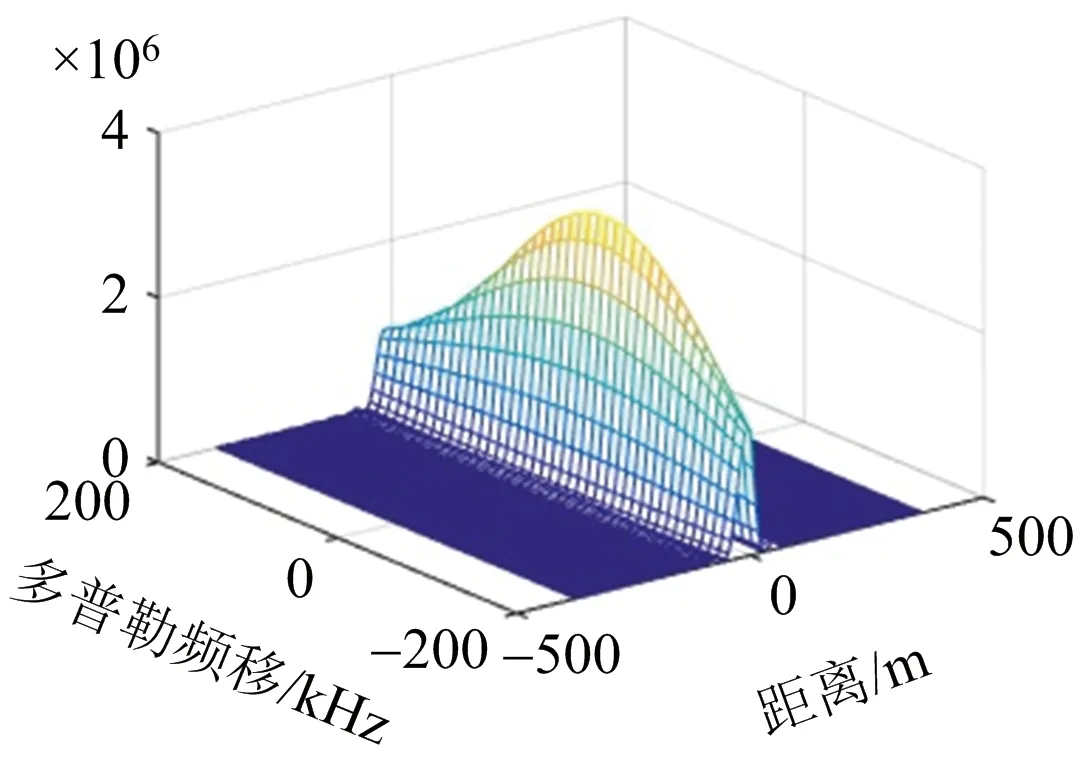
(a) 距離-多普勒模糊函數圖

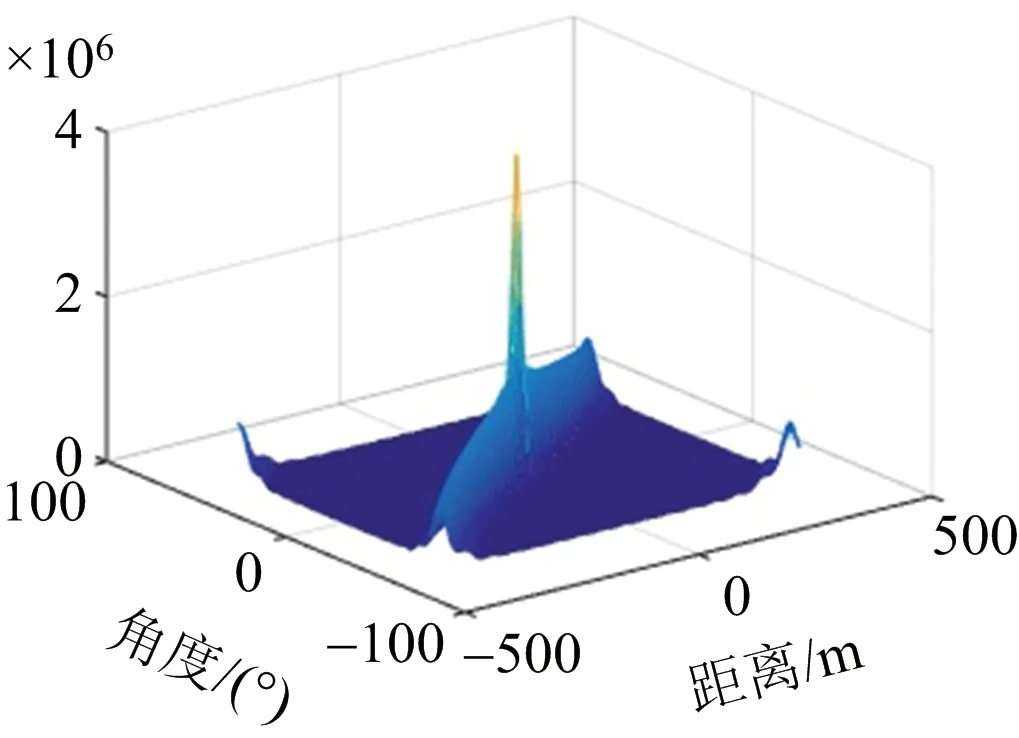
(b) 距離-角度模糊函數圖

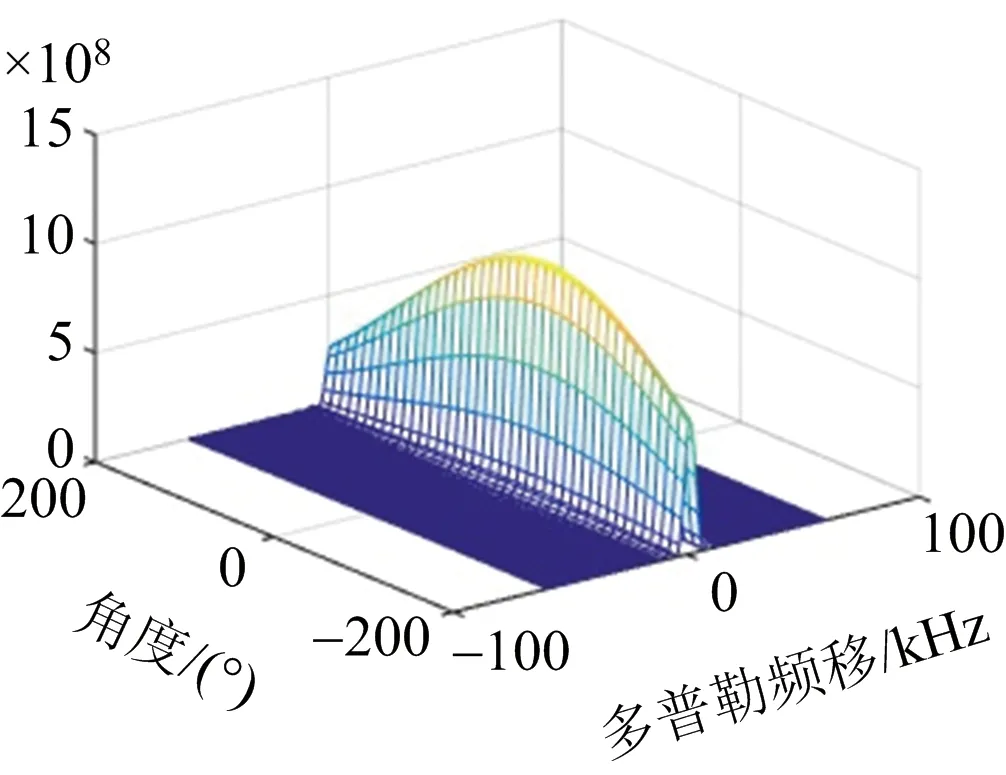
(c) 多普勒-角度模糊函數圖圖5 多普勒頻移為10 kHz時雷達系統的模糊函數圖

根據公式(14)可得，τB與τm,p,d的作用是相同的，在距離(時延)補償后并不會對模糊函數造成影響，根據公式(15)可得，和的作用也是相同的，因此，當轉發站與接收站兩者之間存在相對移動產生的多普勒頻移和目標相對于發射站(轉發站)的相對移動產生的多普勒頻移對模糊函數圖的影響是相同的。

通過仿真得到的模糊圖可知，該雷達系統能夠實現對目標方位和距離的求解，證實了該雷達的可行性。

4 結束語

本文介紹了一種通過在探測鏈路中引入轉發站，以實現遠距離目標探測的新體制雷達。轉發站采用了單個通道實現目標回波的接收并直接錯頻放大回傳，功能簡單，安全可靠。通過轉發站抵近目標的方式，雷達系統獲取更高的信噪比，實現在特定方向上的雷達威力的增強。通過轉發站的合理部署，可以增強在特定海島或海洋方向上的預警能力，對于提升基于本土構建的預警體系的預警能力具有一定的參考價值。