無源雷達直達波參數估計方法研究

蘇漢寧，鮑慶龍，王 森，孫玉朋

(國防科技大學電子科學學院，湖南長沙 410073)

0 引言

在越來越強調電子系統隱蔽攻擊和硬殺傷功能的驅使下，無源探測技術[1]為空間目標隱蔽探測和精確定軌提供了十分重要的手段。基于非合作外輻射源的無源雷達系統通過估計外輻射源的直達波信號的調制參數，構建匹配濾波器，檢測和分析目標反射輻射源發射的信號能量，從而實現對目標的定位和跟蹤[2]。因此，準確快速地估計直達波的參數是無源雷達完成檢測和跟蹤任務的前提。

線性調頻信號(chirp signal)是一種應用非常廣泛的非平穩外輻射源信號，chirp信號的低截獲概率特性也是其廣泛應用在各個雷達體制中的重要原因。在以chirp雷達為外輻射源的無源雷達系統中，參考天線按一定的周期來截獲直達波信號。在一個觀測周期內，chirp信號往往以多分量的形式出現，分量間存在時頻混疊，而且時間不同步。這種廣義形式(占空比η≤100%)并不滿足chirp信號的一般數學表達式(占空比η0=100%)，這使得一些基于最大似然估計[3-4]和基于檢測時頻脊線[5-6]的方法無法直接應用于直達波信號的參數估計。盡管有學者提出在沒有交叉干擾的時頻圖上檢測時頻線段的方法[7]，但這些時頻圖大都因為平滑處理而無法表示信號的瞬時相位，因此估計精度較差，而且缺乏計算效率。

國內學者[8-9]提出了一種基于分數階傅里葉域濾波的信號分離方法，其基本思想是根據chirp信號在某個分數階傅里葉域的稀疏性和FrFT的無損可逆性，將chirp信號分離并恢復為單分量chirp信號，這一思想同樣適用于占空比η≤100%的廣義形式的chirp信號[10]。然而，即使工程上已存在分數階傅里葉變換(Fractional Fourier Transform，FrFT)的快速算法[11]，但在缺少關于調頻斜率先驗信息的條件下，則需要在所有變換階內搜索，這對信號的實時處理帶來了極大的壓力。在工程背景下，非合作chirp雷達信號通常有多套固定的參數模板以完成跟蹤和搜索任務，在不同的時間段內產生不同的頻率參數組合。經過長期的工作積累，不難獲得這些雷達信號的參數模板。因此，在該先驗信息的幫助下，對非合作外輻射源雷達直達波的實時參數估計可以在有限的變換階上實現。

本文將利用分數階傅里葉域濾波方法實現無源雷達系統中直達波的參數估計。本文首先介紹了chirp雷達作為外輻射源時直達波信號的一般形式，然后介紹了基于分數階傅里葉域濾波的多分量chirp信號的參數估計方法，最后通過仿真，分析了該方法處理非合作chirp雷達信號的性能及表現。

1 非合作chirp雷達信號

無源雷達[12-13]作為一種綠色環保、經濟安全的被動探測手段近年來獲得學術界的廣泛關注。以chirp雷達為外輻射源的無源雷達系統實現目標的探測與跟蹤的模型[14]如圖 1所示，a，b，c分別表示非合作chirp雷達與目標的距離、目標與接收機之間的距離、非合作chirp雷達與接收機間的距離；φ表示目標與直達波間的方位角。一般情況下，c是已知的，φ可通過特定的DOA估計算法獲得，因此，只需求得直達波與目標散射回波間的到達時間差ΔTOA=τa+τb-τc，即可求解a，b，c。

圖1 無源雷達目標檢測與跟蹤模型

采樣頻率為Fs的離散chirp序列的數學表達式為

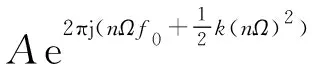
n=1,…,N

(1)

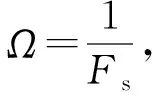
在工程應用中，以采樣頻率Fs采集到的chirp雷達信號可表示為

(2)

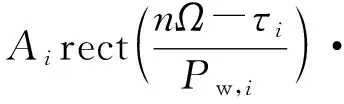
n=1,…,N

(3)

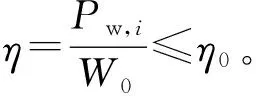
2 分數階傅里葉濾波實現chirp信號分離

連續全脈沖chirp信號的p階分數階傅里葉變換Sp(μ)表達式為

Sp(μ)=FrFTp[s(t)]=

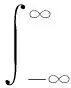
(4)

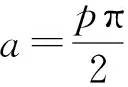
Ka(t,μ)=

(5)

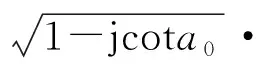
exp(-jπμ2k)δ(csca0-f0)

(6)

當cota0=-k時，chirp信號在p0階分數階傅里葉域表現為沖擊函數，譜峰位置為μ=μ0=f0sina0。對于占空比η<100%的chirp信號，譜峰估計僅能獲得chirp信號在時頻圖上所在直線的調制參數，即

(7)

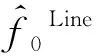
(8)

因此，可通過逆分數階傅里葉變換(inverse Fractional Fourier Transform，iFrFT)將濾波后的分數階傅里葉域信號恢復為單分量時域信號，完成信號分離，該過程如圖 2所示。

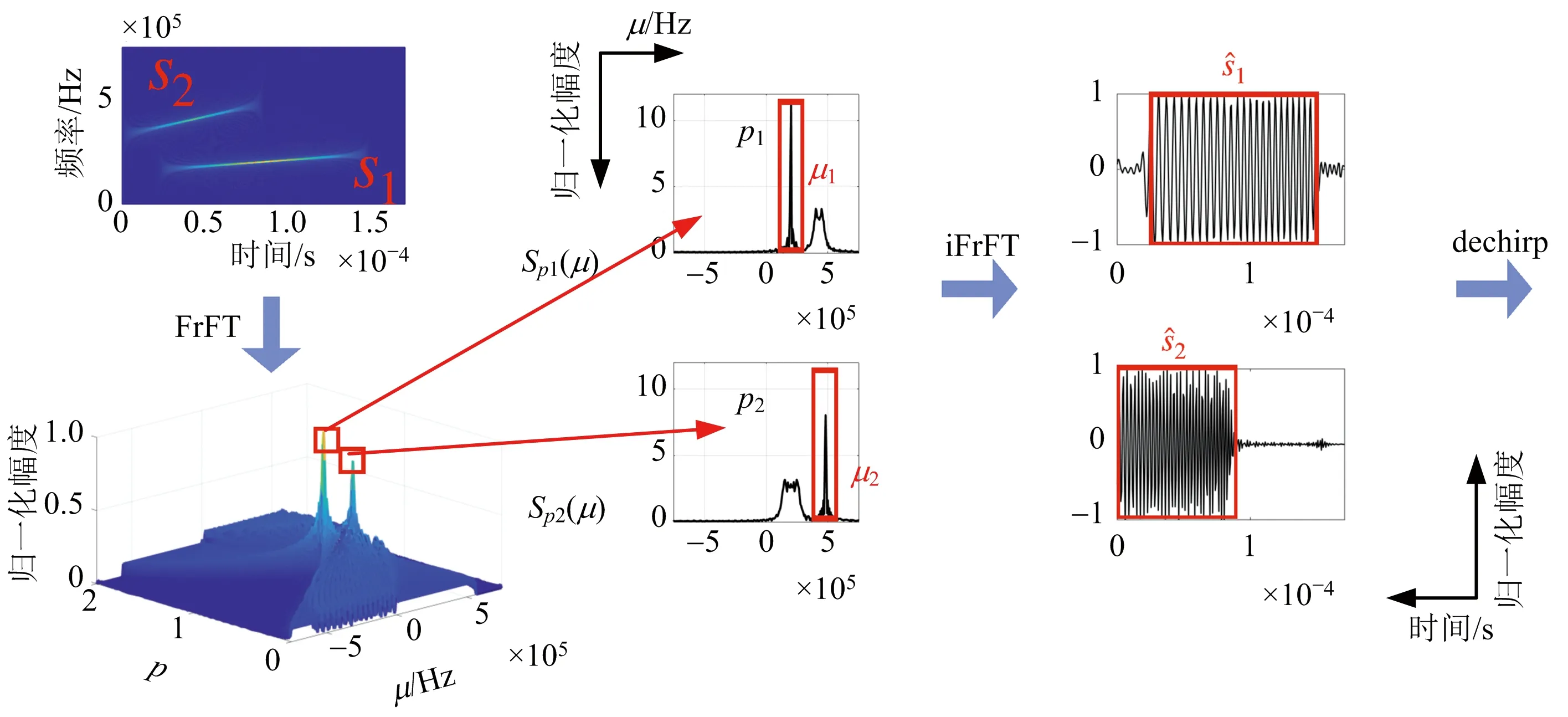
圖2 分數階傅里葉域濾波實現chirp信號分離

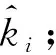
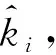
3 直達波信號實時參數估計系統

本節將借助分數階傅里葉域濾波的方法來實現非合作chirp雷達直達波信號的實時參數估計，根據模板信息，系統可以設置多個通道來并行處理一段直達波信號，如圖 3所示，其中第i個通道對應pi階的FrFT處理，只輸出與pi階FrFT匹配的chirp分量的參數。

圖3 直達波信號實時參數估計系統

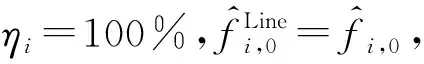
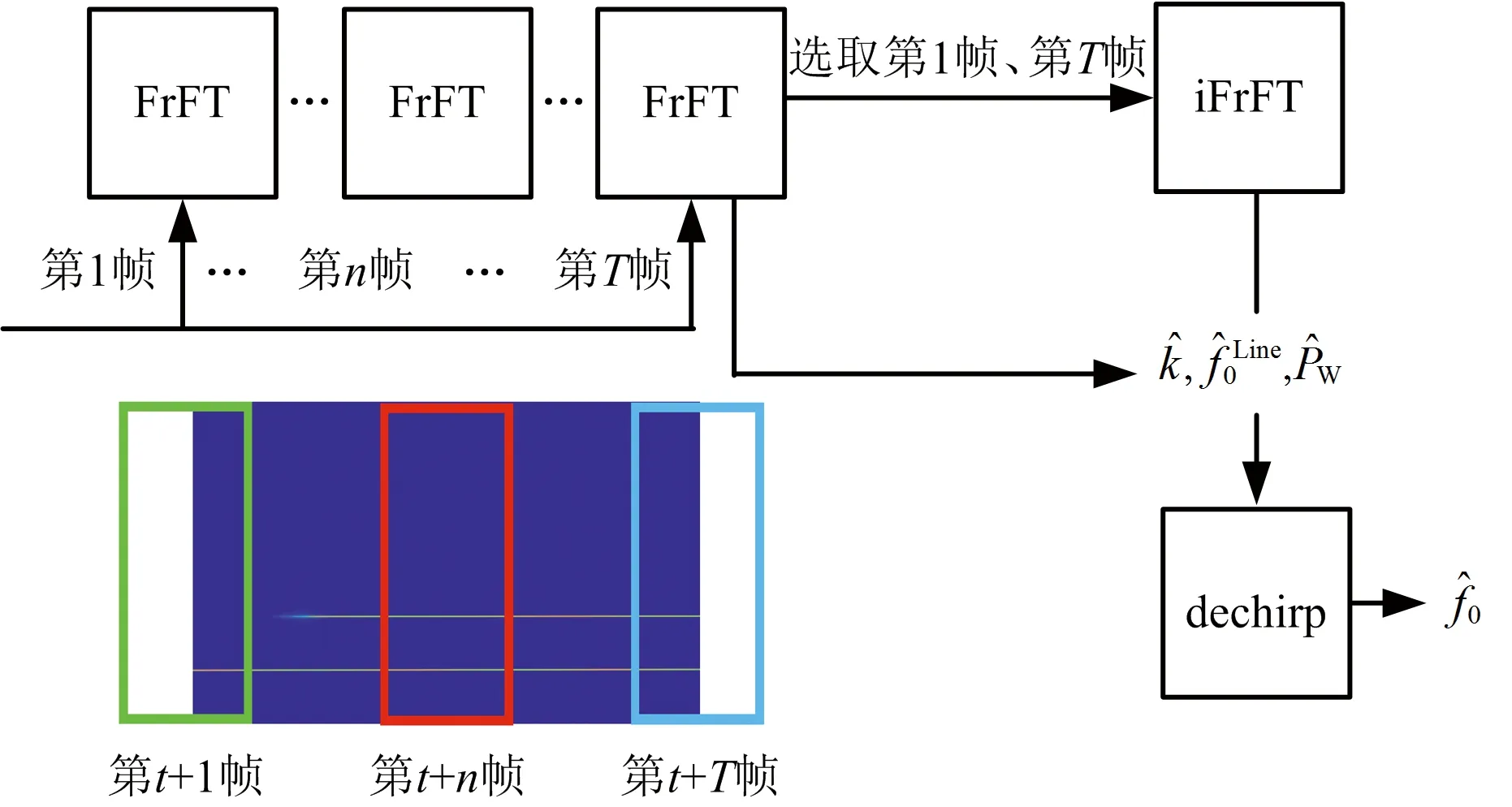
圖4 某通道直達波信號的處理過程

4 實驗驗證分析

接下來以仿真chirp信號為例，來驗證所提方法處理直達波信號的有效性。仿真數據中，采樣頻率Fs為60 MHz，chirp信號帶寬Bi∈{5 MHz，10 MHz，15 MHz}，脈寬Pw,i∈{100 μs，1 ms，10 ms}，中心頻率的選擇滿足奈奎斯特采樣定理。假設這些參數已知，即均為模板庫中可選的參數，則可以設計9路通道對接收的直達波信號進行參數估計，9路通道分別對應不同的變換階p。

估計直達波參數的具體步驟如下：

Step 1: 確定觀測幀的長度。分析模板庫中所有chirp分量的Pw信息，選擇合適尺寸的W0使具有不同Pw的chirp分量占有不同數目的觀測幀T。在本例給出的仿真數據中，3種脈寬所占的采樣點數分別為6 000、60 000和600 000，因此若取W0=8 192/Fs，則3種脈寬可能占有的連續觀測幀數如表 1所示。

表1 脈寬匹配模板

W0選擇不唯一，本例中取W0=8 192/Fs。

Step 2: 模板匹配。由式(7)知，ki與pi存在一一對應的關系，因此，記錄pi階通道下出現沖擊特征的連續幀的長度Ti，可以完成(pi,Ti)與(ki,Pw,i)的匹配。以圖5中的仿真信號為例，圖5展示了某個時間段內觀測幀在直達波信號si{Pw,i，fi,0，Bi=Pw,i×ki}上的滑動情況，信息如下：

·第1幀出現兩個窄帶chirp分量，記為s1{1 ms,1 MHz,10 MHz}，s2{1 ms,2 MHz,5 MHz}，都于第8幀消失。

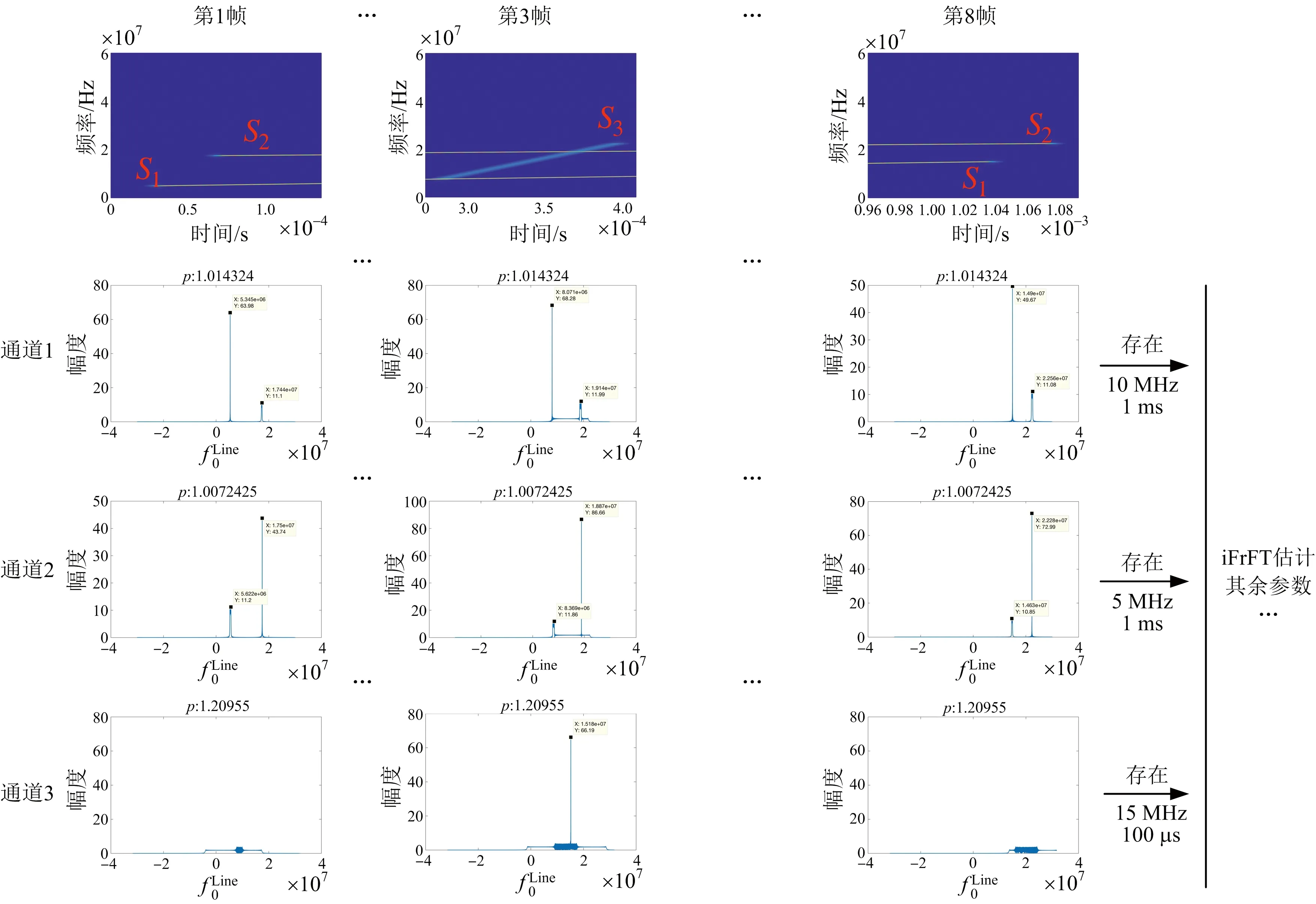
圖5 樣例信號模板匹配過程

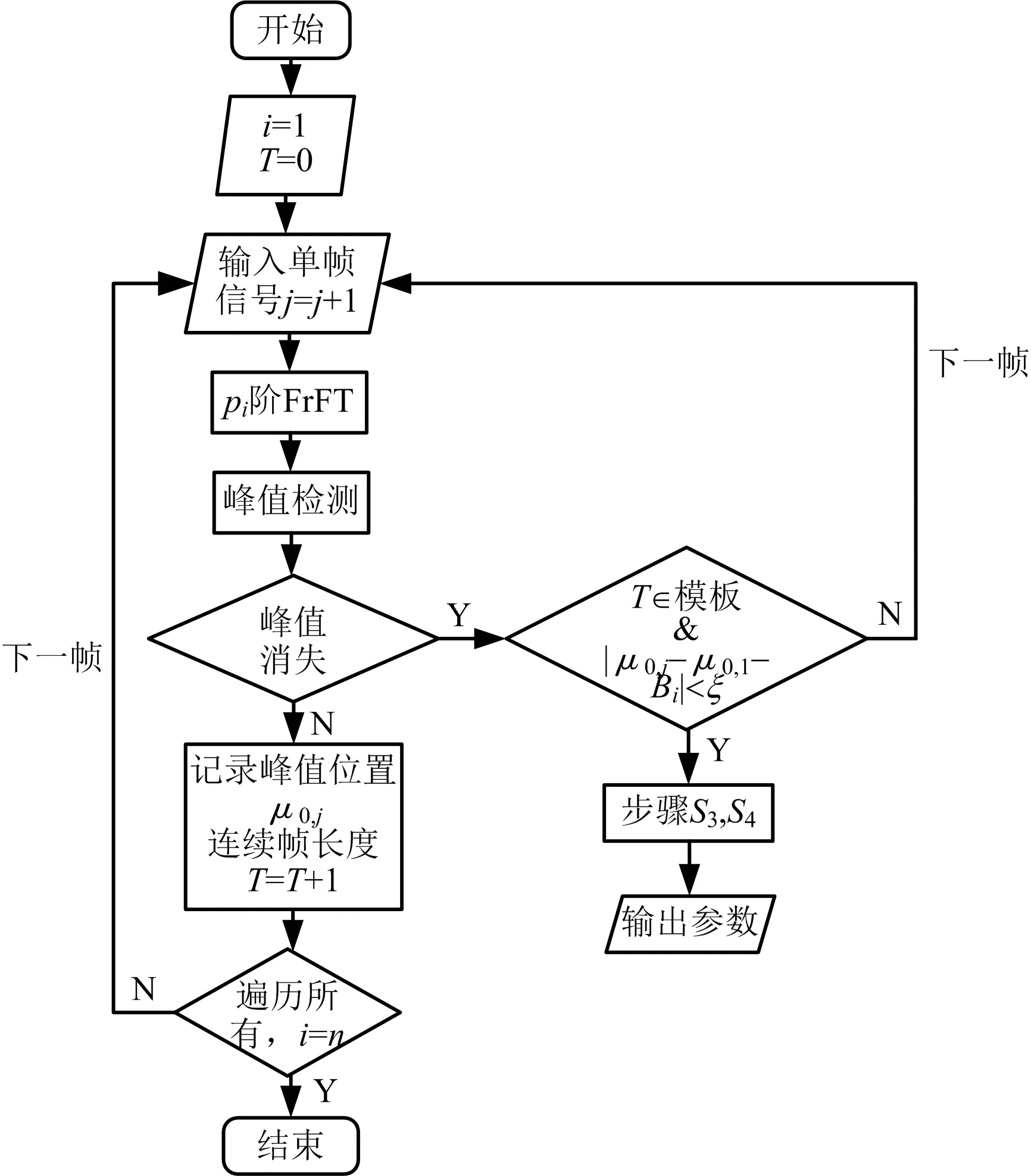
圖6 直達波信號模板匹配流程

·第3幀出現一個寬帶chirp分量，記為s3{100 μs,1.5 MHz,15 MHz}，僅存在于第3幀。

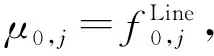
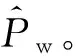
Step 6: 重復Step 2～Step 4。

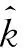
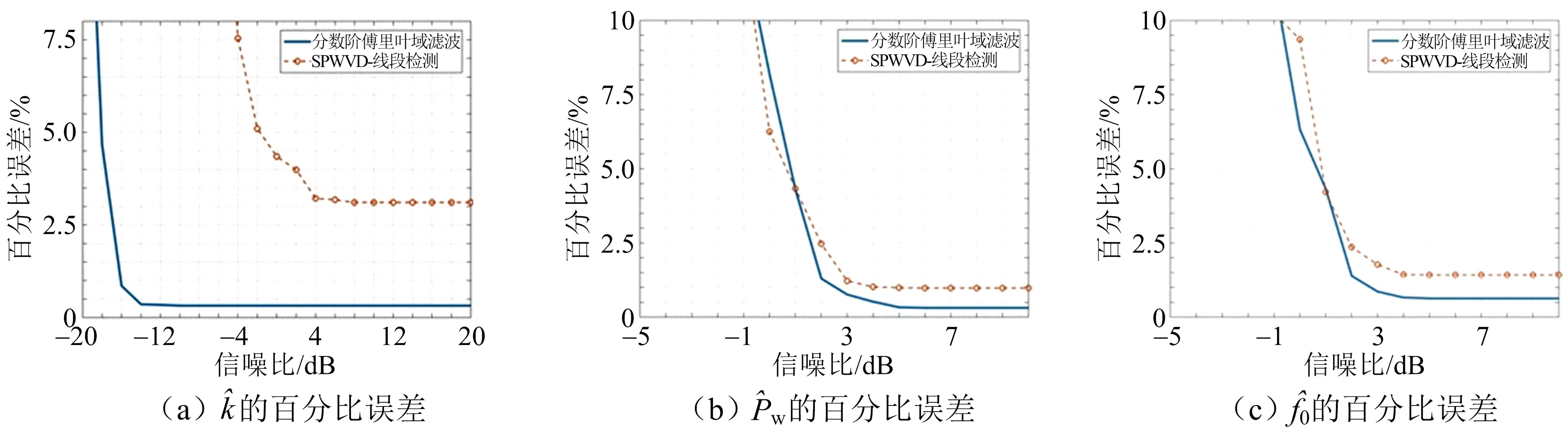
圖8 s1的參數估計誤差曲線

表2 處理100 MB數據的計算效率

由此我們可以得出結論，基于線段檢測的方法由于時頻圖像的模糊而導致低的估計精度，且不適用于低信噪比背景。基于分數階傅里葉域濾波的方法可以在分數階傅里葉域直接完成對k的估計，具有良好的抗噪性。雖然濾波和iFrFT損失了原始信號的部分信息和抗噪性，但對Pw和f0的估計依然可以達到較高的精度。而且，相較于求解全局能量分布的時頻圖像而言，在有限次的分數階上進行信號的分離與恢復無疑大大節省了計算成本，因此，基于分數階傅里葉域濾波的方法擁有更高的計算效率，結合FFT的快速算法，該方法可以在FPGA上實現對已知參數庫直達波的實時估計。

5 結束語

本文通過分數階傅里葉域濾波的方法實現非合作chirp雷達直達波信號的參數估計，本文基于已有的模板庫，設計有限的通道對直達波信號進行實時的參數估計，利用分數階傅里葉變換無損可逆的特性對時頻混疊的chirp信號進行分離和恢復，將多分量chirp信號的參數估計問題轉化為單分量問題，大大提高了復雜工程背景下chirp信號的參數估計精度和計算效率。實驗結果表明，相比基于時頻圖的線段檢測方法，基于分數階傅里葉域濾波的方法能夠達到更高的估計精度，而且易于實現，適用于高采樣速率下的大數據背景。