面向高超聲速飛行器雙重不確定性的自適應狀態估計

馮肖雪，劉 萌，李笑宇，潘 峰,2

(1. 北京理工大學自動化學院，北京 100081；2. 北京理工大學昆明產業技術研究院，昆明 650106)

0 引 言

高超聲速飛行器一般指臨近空間內飛行速度超過5倍聲速的飛行器，具有飛行速度快、反應迅速、突防成功率高等特點[1]，是現今世界各國的研究熱點。高超聲速飛行器工作在大空域、寬速域等復雜多變的飛行環境中，相對于亞聲速及超聲速飛行器其飛行特性有著明顯差異性，具有更強的不確定性，具體體現在：(1)高超聲速飛行器的飛行環境復雜多變，獲得精確的氣動特性非常困難，通過風洞試驗來獲取準確氣動參數的方法并不適用于高超聲速飛行器[2];(2)臨近空間的大氣運動復雜，各種難以預測的擾動對高超聲速飛行器有明顯影響[3];(3)高超聲速飛行器一般機體較輕，機體易產生彈性形變，且超高速飛行下的氣動加熱會降低機體的剛性，造成高超聲速飛行器動力學模型的強不確定性[4];(4)傳感器、執行器等飛行控制系統硬件自身誤差[5]。

由外部復雜的飛行環境以及內部動力學飛行特性帶來的不確定性因素對高超聲速飛行器的飛行狀態有巨大影響，而現今全球范圍內高超聲速飛行器的技術跨度大、成熟度較低且地面試驗和飛行試驗匱乏，所以通過理論研究來提高內外部雙重不確定性因素影響下的系統狀態估計精度，對高超聲速飛行器的故障診斷、軌跡預測[6]、目標跟蹤、抗擾動等領域，以及提升高超聲速飛行器控制系統的安全性和可靠性都具有十分重要的研究意義。高超聲速飛行器的內外部雙重不確定性因素可采用系統狀態演化方程和量測方程中的未知干擾項進行建模[7]，高超聲速飛行器雙重不確定性狀態估計問題則轉化為了含雙重未知干擾項的系統狀態估計問題。目前解決含未知干擾項的狀態估計問題的算法大致可分為以下幾類：

1)狀態演化方程中含有未知干擾項：文獻[8]針對含有狀態未知干擾的系統提出了最小上界濾波器，該濾波器在卡爾曼濾波器的基礎上引入自適應調整因子刻畫狀態未知干擾。但是該方法得到的估計結果并非傳統最小均方誤差意義下最優。文獻[9]針對含未知過程輸入的離散系統提出了基于方程式的未知輸入濾波器，該方法通過矩陣函數估計未知干擾，并且利用未知干擾的估計值計算最優濾波增益。但該方法假設未知干擾和濾波誤差滿足一定的約束條件。文獻[10]針對含未知干擾輸入的多傳感器離散系統，基于典范型分解，給出了不依賴于未知干擾的線性無偏最小方差最優狀態濾波器。但該方法假設系統變換后的量測矩陣和未知干擾分布矩陣滿足解耦約束條件。文獻[11]針對含有狀態未知干擾和執行器故障的線性離散不確定系統，給出了一種基于受限系統模型的狀態估計算法。但是該算法認為未知干擾是范數有界的。

2)量測方程中含有未知干擾項：文獻[12]針對含量測未知干擾的馬爾可夫跳躍線性系統，將系統建模為廣泛意義下具有隨機權重的多面體結構，給出了該結構相應的上界濾波器。文獻[13]針對量測方程含有結構化未知量測干擾的系統提出一種迭代最小上界濾波器，但該方法將結構化未知干擾的方差建模為對角陣。上述方法均使用了基于魯棒估計準則的上界濾波器解決估計問題，但估計結果并非傳統最小均方誤差意義下最優。文獻[14]針對含量測未知干擾系統提出了一種濾波器，基于線性無偏最小方差估計準則，通過構造含拉格朗日因子的性能指標并對其求導給出了濾波器參數設計。但是該方法要求未知干擾分布矩陣的維數不能超過量測的維數。

3)狀態演化方程和量測方程中均含有未知干擾項：文獻[15]針對幅值未知但波形已知的干擾作用于系統的情況，通過構造一個系統輸出并為其設計觀測器進而同時估計狀態變量和未知干擾。文獻[16]考慮狀態方程和量測方程同時受到未知干擾的系統，基于線性無偏最小方差估計準則設計了未知輸入T-S觀測器。但上述兩種方法均假設狀態干擾和量測干擾為相同的干擾。文獻[17]針對狀態方程和量測方程同時受到未知干擾的系統，采用自校正外部模型，給出了基于加權最小二乘遞推算法和卡爾曼濾波器兩種新的狀態估計算法。但是二者均假設未知干擾分布函數已知。文獻[18]針對未知干擾與狀態不獨立情況下的含雙重未知干擾的離散隨機系統，提出了兩階期望最大化算法來辨識未知干擾。但該算法假設未知干擾建模為均值和方差未知的高斯項。文獻[19]針對含有未知干擾的線性時變離散隨機系統，提出了狀態變量和故障同時估計的擴維魯棒三階卡爾曼濾波器。但該方法將未知干擾建模為寬平穩過程的隨機游走噪聲。

總結來看，現有的針對狀態演化方程和量測方程中均含有未知干擾項的狀態估計算法存在以下局限性：(1)要求狀態干擾和量測干擾為相同的干擾。(2)要求未知干擾分布具有一定的先驗信息。對于高超聲速飛行器控制系統，復雜飛行環境下的未知擾動和動力學飛行特性帶來的不確定性從產生機理以及數學模型上都是完全不相同的，也沒有任何先驗信息可取，針對此類問題現有的研究方法束手無策。因此，本文將受到內外部雙重不確定性影響的高超聲速飛行器建模為狀態演化方程和量測方程含有不同未知干擾輸入項的隨機系統，設計了基于自適應方差極小化的遞推狀態估計器。首先建立狀態估計遞推模型，然后解耦濾波誤差中的量測未知干擾，之后引入自適應調整因子刻畫狀態未知干擾，最后利用最小方差估計準則設計了濾波器中的待設計參數矩陣。以外部突風和內部傳感器故障為例，受內外部雙重不確定性因素影響下的高超聲速飛行器仿真實驗驗證了本文算法的有效性。

1 問題提出

考慮線性離散系統

xk+1=Akxk+Bkuk+qk+dk

(1)

yk+1=Ck+1xk+1+ηk+1+Dk+1bk+1

(2)

式中：xk+1∈Rn為系統的狀態向量，yk+1∈Rm為量測向量，uk為已知的控制輸入，qk∈Rn和ηk+1∈Rm分別為滿足假設1的系統噪聲和量測噪聲。dk∈Rn和bk+1∈Rp分別為未知狀態干擾輸入矢量和未知量測干擾輸入矢量。Ak、Bk、Ck+1和Dk+1為適當維數的矩陣。

假設1.過程噪聲qk∈Rn和量測噪聲ηk+1∈Rm分別為零均值的高斯白噪聲并且滿足

(3)

式中：Qk≥0為系統噪聲方差陣，Rk+1≥0為量測噪聲方差陣，δkj為Kronecker符號。

假設2.rank(Dk+1)=p,m>p，rank(*)代表矩陣的秩。

注1.假設1采取的高斯白噪聲是濾波估計、信號處理、通信系統、深度學習等諸多領域理論研究中最常采用的噪聲模型，具有公式簡潔、便于分析計算、算法設計等優勢。依據中心極限定理，高斯白噪聲可以很好地模擬真實系統中的加性噪聲。過程噪聲和量測噪聲不相關的假設可以避免算法推導過程中交叉項的引入，降低公式復雜度。假設2是實現量測未知干擾解耦的基本條件，要求量測向量維數m必須大于未知量測干擾維數p，否則便沒有足夠的信息來解耦未知量測干擾。

狀態未知干擾dk項除了可以描述加性干擾外，還可以描述各種系統建模的不確定性，例如系統建模過程中的非線性項、模型降階簡化以及關鍵參數擾動等引入的狀態未知干擾輸入。量測未知干擾Dk+1bk+1可以描述傳感器標定誤差、外界環境對傳感器的干擾以及信息傳輸過程中的信息丟失等引入的量測未知干擾。當dk=0，Dk+1bk+1不為0時，式(1)和(2)表示的系統等同于只受到量測干擾的系統[20]。當Dk+1bk+1=0，dk不為0時，式(1)和式(2)表示的系統等同于只受到狀態干擾的系統[21]。此外，若將狀態未知干擾建模為dk=Ekεk，則系統模型等同于狀態干擾分布矩陣已知的模型[19]，若要求dk=bk+1，則系統模型等同于狀態干擾與量測干擾相同的模型[15-16]。由此可知，式(1)和式(2)可以表征更為普遍意義下含雙重未知干擾的隨機不確定離散系統數學模型。

本文的目的是針對狀態方程和量測方程含不同未知干擾(且無任何先驗信息)的高超聲速飛行器系統，基于自適應估計的思想，設計一種基于自適應方差極小化的遞推狀態估計器。

2 基于自適應方差極小化的遞推狀態估計器設計

針對式(1)和式(2)建模系統的狀態估計問題，最直觀的解決辦法是對狀態未知干擾和量測未知干擾進行雙重解耦，獲取自適應方差極小化意義下的最優估計。但由于本文考慮的系統中狀態未知干擾的干擾分布矩陣未知，且這是采用干擾解耦方法的根本條件，因此本文建模的系統無法采用文獻[23]中干擾解耦的方法實現狀態干擾解耦。另外，采用干擾解耦的辦法對量測干擾實施解耦會犧牲待設計矩陣參數的部分自由度，而剩余的自由度能否對狀態干擾實施二次解耦也是值得商榷的問題，需要針對系統模型具體問題進行具體分析。此外，針對本文所考慮的系統，擴維卡爾曼濾波[19]也是一種較為直接的方法，該方法通過將未知狀態干擾以及量測干擾引入擴維狀態變量，較好地解決了狀態干擾和量測干擾之間的耦合問題。但由于雙重干擾的強不確定性，擴維卡爾曼濾波的計算量和濾波誤差會隨著擴維狀態變量的維數上升而急劇增加。文獻[8]中魯棒估計方法很好地規避了上述所提的參數設計自由度不足以及濾波誤差發散的問題，魯棒估計方法通過引入自適應調整因子來刻畫未知干擾，無需犧牲待設計濾波增益矩陣的自由度。本文針對狀態方程和量測方程含雙重未知干擾的隨機不確定系統，擬采用干擾解耦的辦法實現量測未知干擾解耦，而針對狀態干擾則采用引入自適應調整因子求取自適應狀態估計的方法。

本文針對含雙重干擾系統的狀態估計問題，提出了一種基于自適應方差極小化的遞推狀態估計器。首先建立狀態估計遞推濾波器，實現濾波誤差中的量測未知干擾解耦，之后引入自適應調整因子刻畫狀態未知干擾并得到了最小上界濾波誤差協方差矩陣，最后利用最小方差估計準則設計了濾波器中的量測增益反饋矩陣。

2.1 量測干擾解耦遞推濾波器設計

針對系統(1)～(2)，設計具有如下形式的狀態估計遞推濾波器

(4)

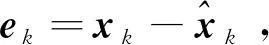
ek)+TkBkuk+Lk+1(Ck+1xk+1+ηk+1+

Dk+1bk+1)=Fk(xk-ek)+TkBkuk+Lk+1·

Ck+1(Akxk+Bkuk+qk+dk)+Lk+1ηk+1+

Lk+1Dk+1bk+1=(Fk+Lk+1Ck+1Ak)xk-

Fkek+(Tk+Lk+1Ck+1)Bkuk+Lk+1Ck+1·

(qk+dk)+Lk+1ηk+1+Lk+1Dk+1bk+1

(5)

聯立式(1)和式(5)得到k+1時刻濾波誤差為

(I-Lk+1Ck+1-Tk)Bkuk+(I-Lk+1Ck+1)·

(dk+qk)-Lk+1ηk+1-Lk+1Dk+1bk+1

(6)

對任意的未知輸入bk+1和dk,為了實現量測干擾和濾波誤差解耦，引入如下的解耦約束條件。

(7)

將式(7)代入式(6)，狀態估計誤差化簡為

ek+1=Fkek-Lk+1ηk+1+(I-Lk+1Ck+1)(dk+qk)=

(I-Lk+1Ck+1)Akek-Lk+1ηk+1+Tk(dk+

qk)=Tk(Akek+dk)+Tkqk-Lk+1ηk+1

(8)

根據濾波誤差方程(8)，可得濾波誤差方差陣為

(9)

式(9)中的狀態未知干擾dk阻礙了濾波協方差的計算，需要引入自適應調整因子αk+1(αk+1≥1)刻畫狀態未知干擾并定義濾波誤差協方差的上界為

(10)

2.2 自適應調整因子設計

自適應調整因子可以通過濾波殘差協方差矩陣求取。首先計算濾波殘差：

(11)

對上式左乘Lk并計算濾波殘差協方差Vk+1，利用約束條件(7)將量測干擾從濾波殘差中解耦可得：

(12)

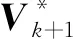
(13)

其中自適應調整因子的求解方法由定理1給出。

定理1.如果以下三個條件均滿足：

2)Ck+1是滿秩的，即rank{Ck+1}=n

(14)

(15)

(16)

集合Ωk+1為

(17)

證.

1) 最優自適應調整因子的存在性：

定義中間變量ΔΨk為

(18)

由式(12)～(13)得：

(19)

由Lk+1Ck+1滿秩可得：

ΔΨk≥0

(20)

由Tk+1滿秩以及式(9)～(10)可得：

(21)

故可得到下列不等式：

(22)

(23)

2) 最優自適應調整因子的求解：

(24)

(25)

(26)

由式(25)～(26)有

(27)

(28)

結合式(22)～(23)有

即式(14)～(15)成立。

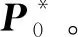
(29)

(30)

(31)

2.3 量測增益反饋矩陣設計

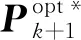
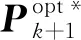
(32)

式中:Λk+1，H和G為中間變量。

(33)

(34)

(35)

證.

應用最小方差估計準則，并由約束條件(7)可引出如下輔助方程：

(36)

將式(31)代入式(36)得：

tr{Qk+Lk+1Ck+1Qk(Lk+1Ck+1)T}-

(37)

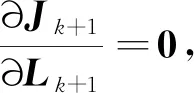
(38)

定義中間變量H和G如式(33)～(34)，則式(38)可以表示為

(39)

將式(39)和約束條件(7)聯立得到矩陣方程組：

(40)

寫為分塊矩陣形式：

(41)

由假設2可知分塊矩陣方程的系數矩陣的逆存在，解分塊矩陣方程(41)得：

即式(32)和式(35)成立。

2.4 算法實現步驟

基于2.1、2.2和2.3節的推導和證明，針對高超聲速飛行器雙重不確定性系統，本文所提的基于自適應方差極小化的遞推狀態估計器的計算步驟如下：

1)k=1，設置狀態初值x0，誤差協方差初值P0；

2)由式(11)計算殘差γk+1；

6)將參數代入式(33)和式(34)計算中間變量H,G；

7)將中間變量H和G代入式(35)計算Λk+1；

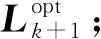
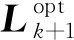
11)k+1，返回步驟2)。

3 仿真校驗及結果分析

3.1 仿真環境

采用文獻[24]給出的高超聲速飛行器縱向小擾動線性模型進行仿真驗證。其中：狀態變量為x=[v,γ,α,q,h]T(v,γ,α,q,h分別為飛行速度，航跡傾角，迎角，俯仰角速度和高度)，控制輸入為uk=[δe,η]T(δe,η分別為升降舵偏角，油門設定)，狀態方程中Ak，Bk和過程噪聲協方差矩陣Qk分別為

未知狀態擾動dk設定為外部突風[21]，設置如下：前10 s未知干擾為0，第10 s到第20 s受到幅值為1的階躍響應，第20 s到第30 s受到幅值為-1的階躍響應，從第30 s一直到第100 s未知干擾始終為0。

控制輸入為uk=[-0.2389, 0.1566]T，初始狀態設置x0=[4525.6, 0, 0.978, 0, 30000]T，狀態協方差P0=0.12I5×5。

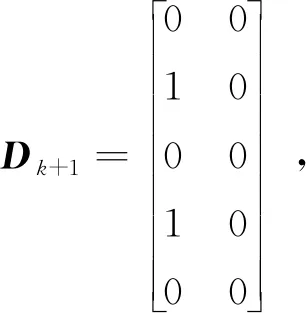
3.2 系統狀態估計結果及分析

本節對所提出的基于自適應方差極小化的遞推狀態估計器(AVMRE)的有效性進行驗證，并與KF和最小上界濾波器[8](Minimumupper-bound filter, MUBF)進行對比。圖1和圖5分別為不同算法對第一維和第五維狀態變量的估計效果對比，這兩維度都不受突風和傳感器故障的影響，可以看出本文所提算法、MUBF與KF算法估計效果相差不大，都可較好地跟蹤真實值。

圖2為第二維狀態變量估計效果對比，由狀態干擾dk和量測干擾Dk+1bk+1可知該變量只受到傳感器故障影響，當量測變量在50～70 s受到傳感器故障影響時，本文所提算法對故障干擾進行了解耦設計，故估計效果較好，而未考慮故障干擾解耦的KF和MUBF估計效果不佳。

圖3為第三維狀態變量估計效果對比，由狀態干擾dk和量測干擾Dk+1bk+1可知該維度變量只受到突風干擾影響，可以看出本文所提算法和MUBF由于引入自適應調整因子刻畫突風干擾，進而在0～50 s的估計值較好地跟蹤上了真實值，而KF由于忽略了突風的影響導致估計效果不佳。同時可以看出由于傳感器故障的影響，MUBF和KF的量測值已經產生了偏差，導致相應維度的狀態估計效果也偏離了真實值。

圖4為第四維狀態變量估計效果對比，可以看出本文算法和MUBF算法受到突風干擾估計效果相差不大，而KF算法估計效果不佳。系統在50～70 s受到故障干擾， KF和MUBF由于忽略了故障干擾的影響導致估計效果較差，本文算法通過對故障干擾進行了解耦設計，故估計效果依然較好。

為了更清晰地對比三種算法的估計性能，下面給出了100次蒙特卡洛仿真下狀態估計RMSE對比。為了節省篇幅，只給出了第三維和第四維的結果圖，可以看出本文所提算法的RMSE較小，而KF和MUBF在50～70 s由于傳感器故障的存在，兩種算法的RMSE發生了突變。總結來說，從圖6可以看出，本文所提算法對于單獨受到突風干擾或傳感器故障影響的高超聲速飛行器的狀態估計效果較好；從圖7可以看出，對同時受到突風和傳感器故障雙重干擾影響的高超聲速飛行器，本文所提算法依

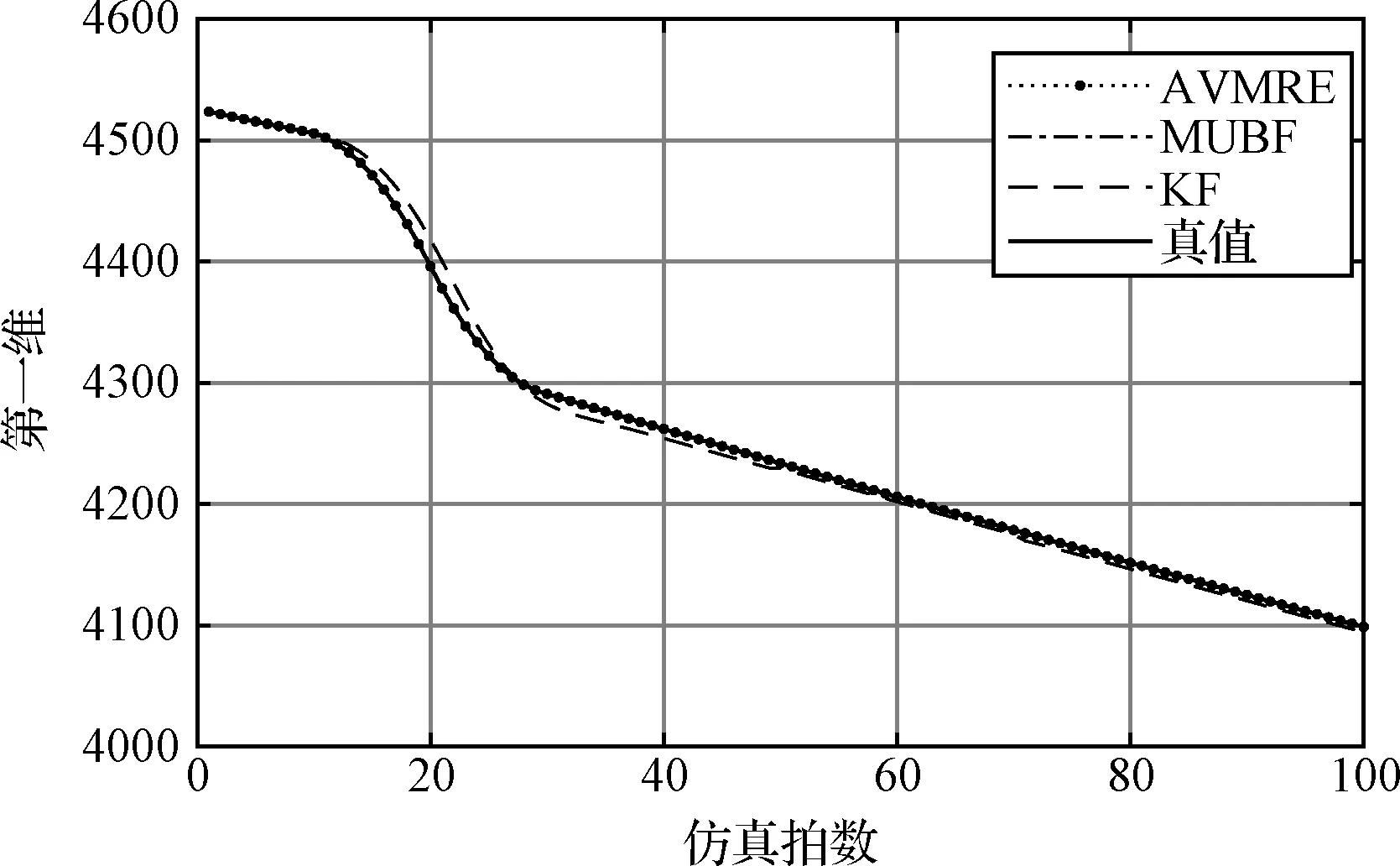
圖1 第一維狀態估計對比

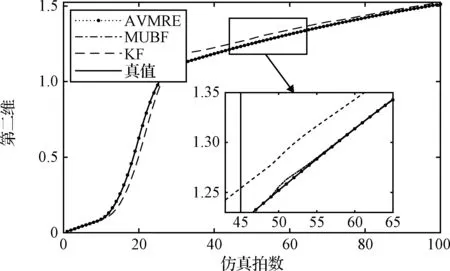
圖2 第二維狀態估計對比

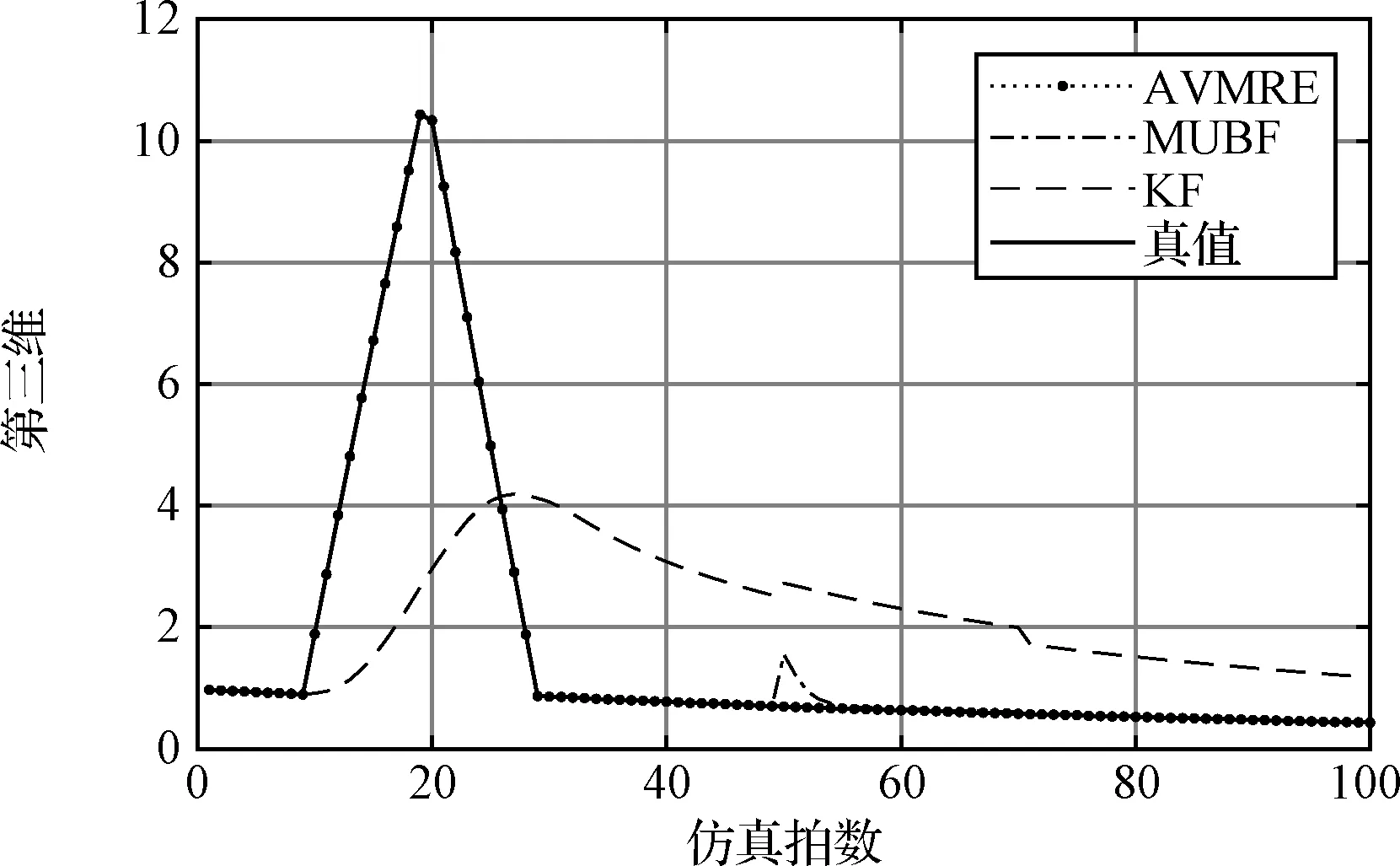
圖3 第三維狀態估計對比

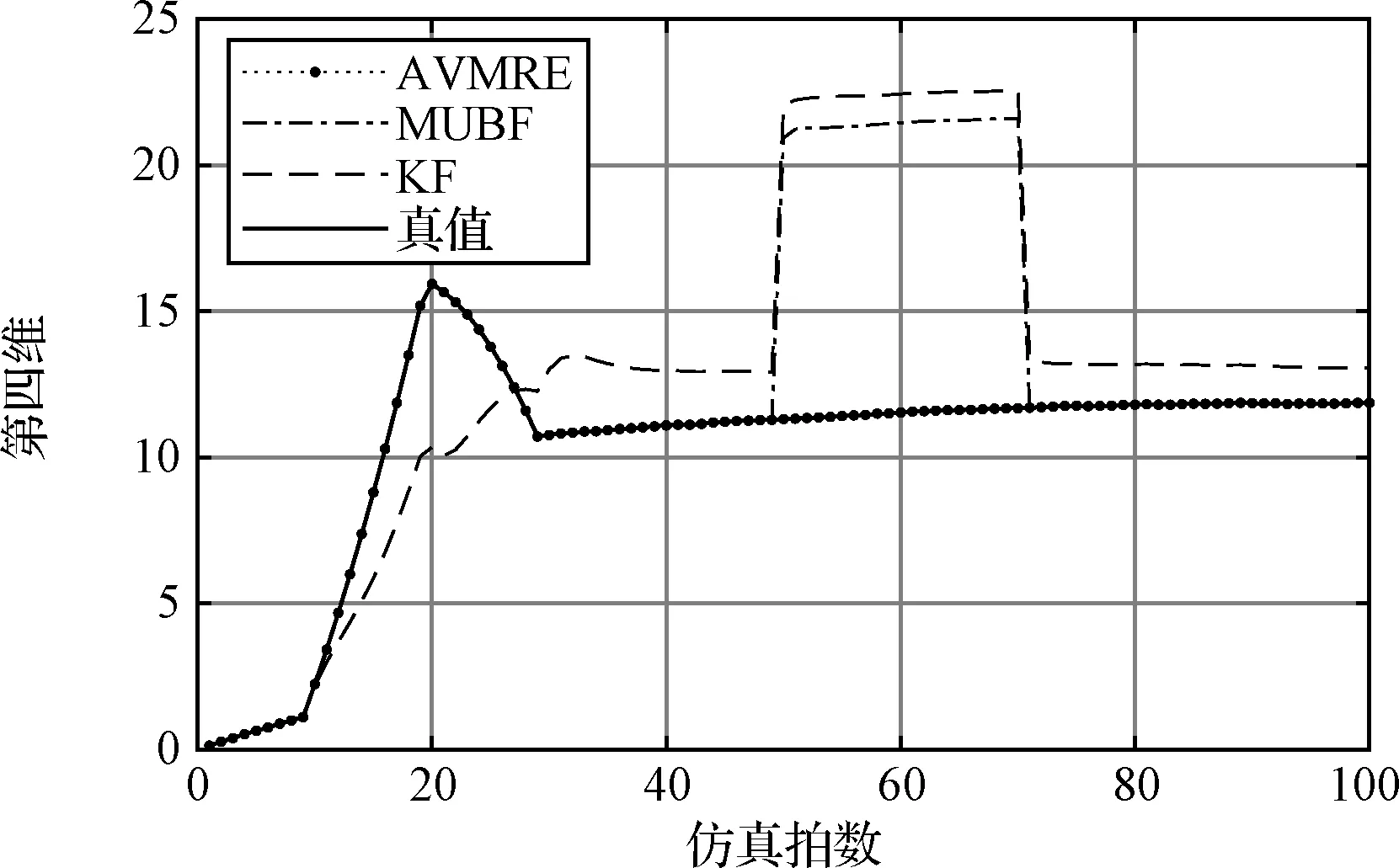
圖4 第四維狀態估計對比

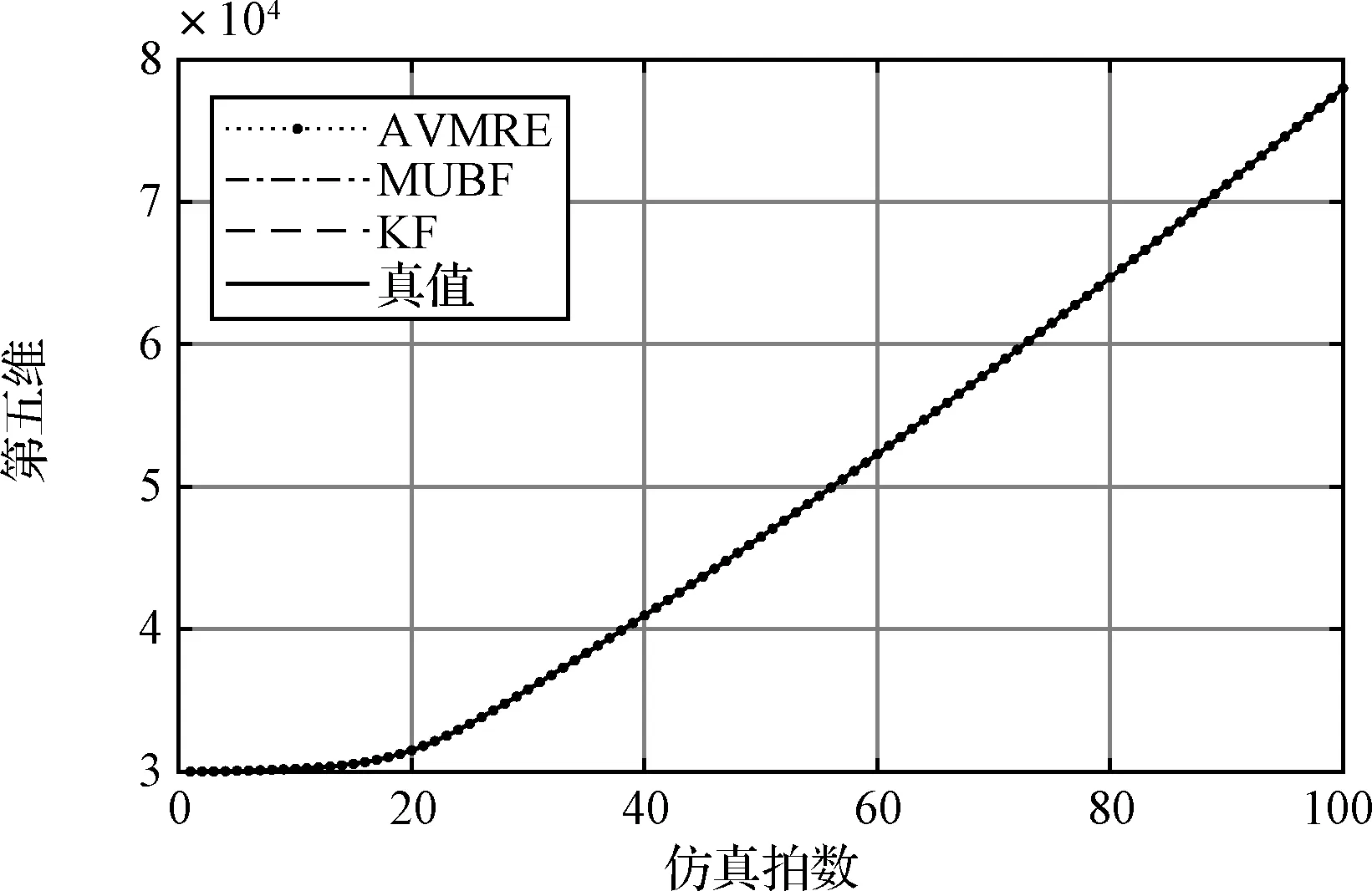
圖5 第五維狀態估計對比

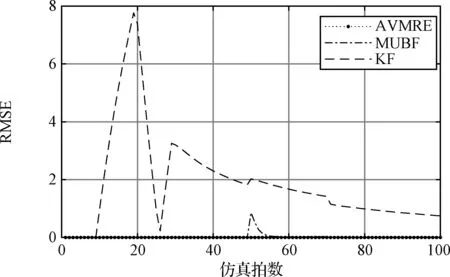
圖6 第三維的狀態估計RMSE對比

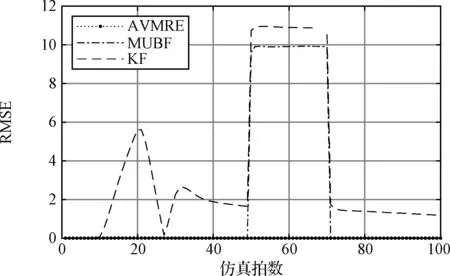
圖7 第四維的狀態估計RMSE對比

然可以獲得令人滿意的狀態估計結果。

4 結 論

本文將高超聲速飛行器中的不確定性因素建模為未知干擾輸入項，針對狀態方程和量測方程含有不同未知干擾輸入的高超聲速飛行器系統狀態估計問題開展了研究，提出了一種基于自適應方差極小化的遞推狀態估計器。首先建立了狀態估計遞推濾波器，實現狀態估計誤差中的量測未知干擾解耦，之后引入自適應調整因子刻畫狀態未知干擾并得到了最小上界估計誤差協方差矩陣，最后，利用最小方差估計準則設計了濾波器中的量測增益反饋矩陣，實現了自適應方差極小化意義下的狀態估計。以外部突風和內部傳感器故障為例，受內外部雙重不確定性因素影響下的高超聲速飛行器仿真實驗驗證了本文算法的有效性。