桁式組合拱橋拆橋過程穩定性分析

楊林愷， 周 聰

(江西省公路科研設計院有限公司， 江西 南昌 330002)

0 引言

桁式組合拱橋施工特點在于采用人字桅桿吊機進行化整為零的吊裝施工，其整體結構跨越能力強，施工簡便，在基建初期發展飛速。面對日益增長的交通壓力，部分桁式組合拱橋已難以滿足荷載要求。通過對已建成的桁式組合拱橋檢測發現，其中可以在現行荷載等級下正常服役的比例不到一半，部分橋梁需進行拆除。由于桁式組合拱橋的獨特受力特性，在進行節段吊裝拆除主拱圈階段易產生結構失穩破壞，導致安全事故發生。目前國內外通常對成橋階段主拱圈進行直接失穩研究，如PI[1]對拱圈的彈性彎扭屈曲特性進行了分析，以拱圈長度作為自變量參數，建立了分析拱圈彈性彎扭屈曲特性的能量方程，考慮了進行主拱圈分析時的翹曲剛度影響；MESSAOUDI[2]在曲桿小變形理論的基礎上計算拱圈結構的側向臨界彎矩，以圓弧的曲率作為分析參數對拱圈的面外屈曲公式進行了推導，并提出了非保向力的概念；肖光宏等[3]以中承式鋼管混凝土桁式拱橋為依托，同時考慮材料非線性與幾何非線性對主拱圈施工階段的穩定性進行分析，對比吊桿橫梁對不同施工階段的穩定性變化，得出主拱圈穩定與加載方式有關的結論；袁海慶等[4]在主拱圈合攏施工前的節段對處于脫離支架的半跨拱圈建立了有限元模型，對施工階段的各種影響因素進行參數化分析，為施工階段的優化結構幾何參數以及力學參數提供參考依據；謝能剛等[5]對主拱圈的動穩定性進行了研究，提出了表征主拱圈動穩定能力的能量函數，以拱壩拱圈結構為例對其地震作用下的響應分析，對結構抗震的幾何參數取值進行了優化，提高了拱圈的抗震能力。由此可見，對桁式組合體系的主拱圈拆除工作的研究還較少，為保證拱橋拆除施工階段的主拱圈穩定性，有必要對拆橋施工穩定性進行進一步分析。

1 拱橋穩定性理論分析

拱橋的穩定性分析主要圍繞結構處于平衡狀態時，在外力作用下，產生了喪失當前穩定狀態的變形或發生不可恢復的塑性變形，通常失穩可以分為以下2種失穩類型。

1.1 單拱面內屈曲失穩

其受力分析可以簡化為兩端鉸接的理想受壓桿件，其計算理想受壓桿件的屈曲臨界荷載公式[6-7]如下所示：

(1)

式中：EI為受壓桿件截面的結構剛度;L為受壓桿件沿受壓方向的長度。

對于桁式組合拱橋而言，其設計拱軸線與自重和活載作用下的壓應力線應重合，主拱圈在均布荷載足夠大的情況下會產生除軸向壓縮變形外的彎曲變形，此時若荷載繼續增加，主拱圈結構將發生不平衡的分支失穩變形，此失穩類型稱之為面內屈曲失穩變形。將主拱圈力學模型簡化為無鉸拱模型，其屈曲形式如圖1所示。

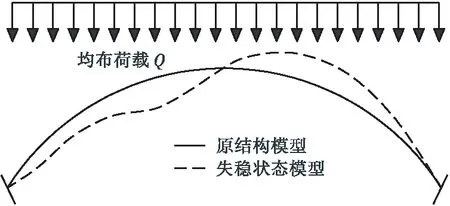
圖1 無鉸拱面內屈曲失穩形式

1.2 單拱面外屈曲失穩

面外屈曲失穩又稱為第2類穩定問題[8]，對于桁式組合拱橋主拱圈而言，當上部結構的荷載形式為均布力加上不對稱力時，拱圈結構同時具有水平方向和豎直方向的位移，一旦作用力達到臨界荷載，變形急劇增大，從而導致結構失穩。無鉸拱屈曲失穩如圖2所示：

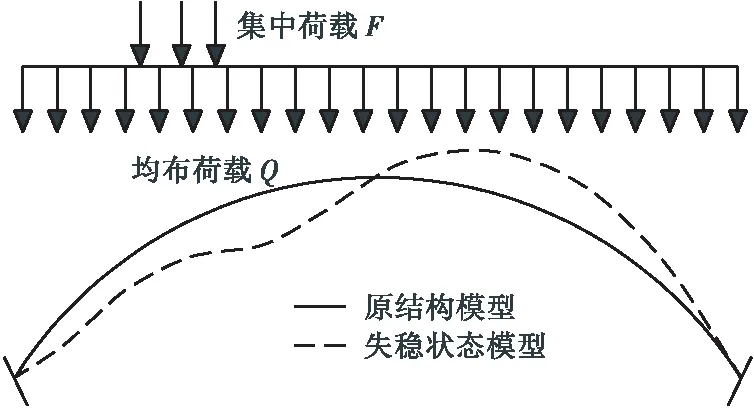
圖2 無鉸拱面外屈曲失穩形式

對于桁式組合拱橋拆橋研究而言，其橋梁由于服役荷載、施工等因素影響出現不同程度上的病害，故其更符合主拱圈面外屈曲極值點失穩的特性。

2 桁式拱橋穩定性空間分析

2.1 工程概況

貴州某桁式拱橋主孔跨徑為130m預應力混凝土桁式組合拱，兩岸邊孔均為門式剛構，全橋孔跨布置為(15+130+15)m，全長177m。全橋共分為9個節段，長度為(15+14+11+10.5+29+10.5+11+14+15)m(29m為實腹段)。上弦在2、3節點之間斷開，形成斷縫。上弦采用88 cm×104cm小箱，懸拼就位后，兩桁片間再加蓋頂、底板及6cm現澆層，組成700 cm×110cm三室單箱截面，作為上弦整體受力截面。下弦采用88 cm×130cm小箱，懸拼就位后，兩桁片間再加蓋頂、底板，組成700 cm×130cm三室單箱截面。斜杠由2個分離式箱組成，其間以橫系梁連接，兩箱截面均為70 cm×88cm，壁厚14cm。取拆橋施工過程中主拱圈拆除時的施工階段作為最不利分析階段進行分析，主拱圈拆除前施工階段橋梁示意如圖3所示。

2.2 桁式組合拱橋拆橋方案

2.2.1拆橋方案

橋梁建設在施工設計階段，無論施工方法還是受力計算均已較為完善，而對于橋梁拆除施工階段的相關研究則較少。考慮到此工程實際情況，橋位上游位置現為水庫，若采用爆破施工可能對水庫產生影響，故決定采用倒拆法，逐步拆除其構件，同步施工運離現場。桁式組合拱橋拆除實施難點主要有： ① 預應力構件過多，截斷有難度; ② 施工過程中存在結構體系轉化; ③下弦桿屬于全橋連續,施工困難。

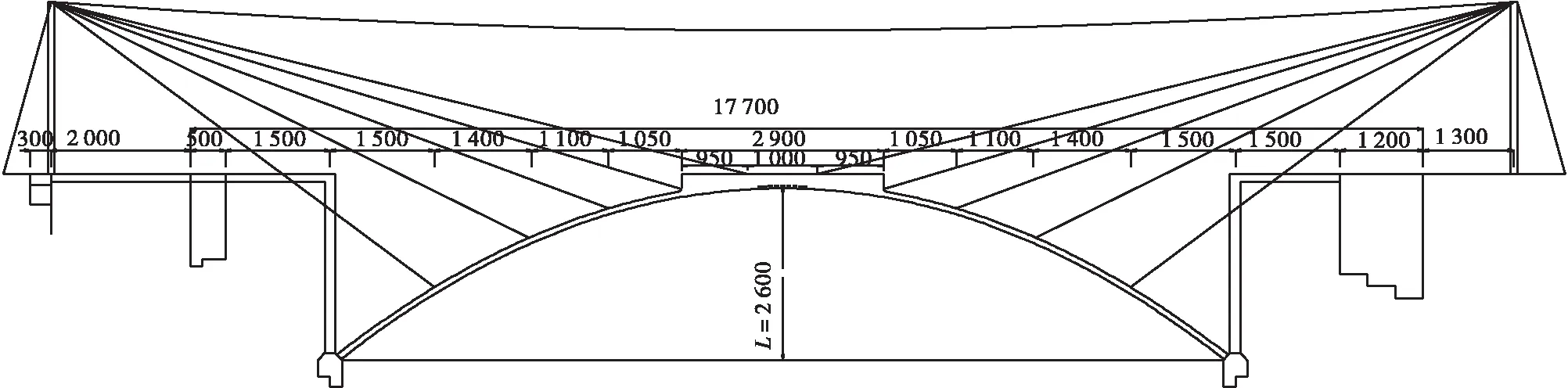
圖3 主拱圈拆除前施工階段橋梁示意圖(單位： cm)

在拆橋的實施過程中要密切關注拱腳結構的應力水平情況，并且控制主拱圈的位移，嚴格控制主拱圈的軸線在同一水平面，并且對拱頂的應力情況進行監測，控制其開裂水平，保證人員安全，具體提出以下的拆除施工方案(見圖4)。

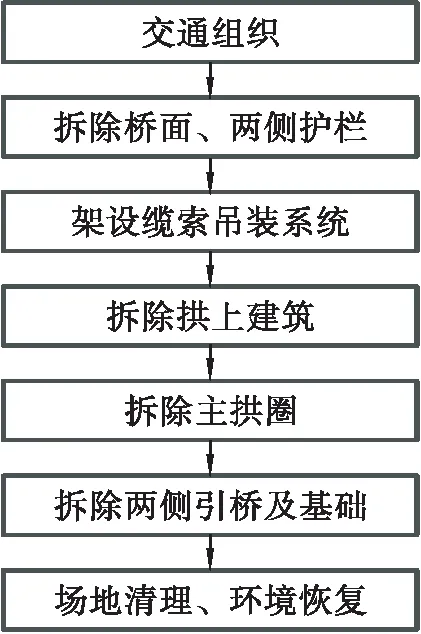
圖4 拆除施工方案

2.2.2扣索設計

在桁式組合拱橋拆除施工過程中，主要是對扣索進行有效布置，同時根據施工階段不斷調整內力數值。扣索布置原則如下： ①扣索索塔應盡量處于受壓狀態，其受力狀態以可簡化為小偏心受壓構件為宜； ②同一施工階段的扣索內力盡量均勻； ③滿足經濟性原則，如控制扣塔高度，當有施工條件直接采用巖錨等。浪風索主要為施工過程中的主拱圈結構提供橫向約束剛度，浪風索在主拱圈的錨固位置與扣索位置相同，對稱布置最大程度上保證主拱圈的橫向穩定。

2.3 施工階段主拱圈穩定性分析

首先建立橋梁有限元模型，空間模型采用7自由度模型，包括3個平面線性自由度、3個轉動自由度以及翹曲自由度，建立拆橋有限元模型時，考慮扣索的錨固作用，扣索的邊界條件簡化為固定約束，根據固定約束的反力以及力學分解原則得到扣索內力以及索塔壓力。主拱圈的受力結構屬于無鉸拱結構，其有限元模型如圖5所示。

圖5 拆橋有限元分析模型

主拱圈在本身自重荷載作用下會產生相應變形，在對主拱圈進行穩定性分析時，需要考慮此部分已存在的豎向位移作為初始位移進行分析，將自重荷載產生的位移反向加到模型節點的坐標上，作為初始位移進行桁式組合拱橋拆橋模型的振興分析。不同失穩模態特征下的穩定系數見表1。

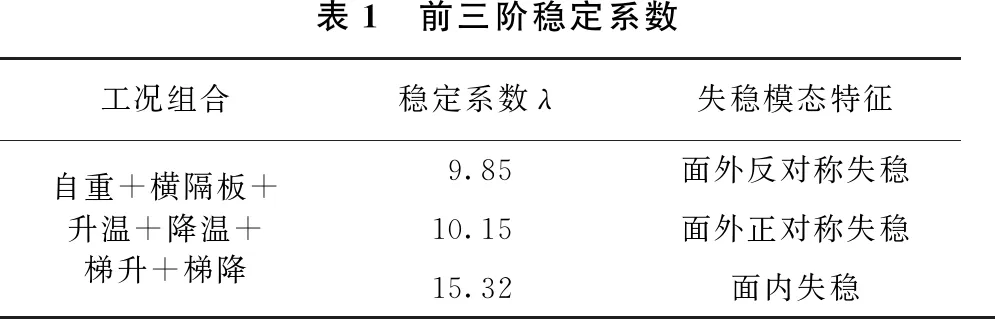
表1 前三階穩定系數工況組合穩定系數λ失穩模態特征9.85面外反對稱失穩自重+橫隔板+升溫+降溫+梯升+梯降10.15面外正對稱失穩15.32面內失穩

2.4 考慮初始缺陷的非線性穩定性分析

在上述對拆橋階段的拱圈有限元模型進行分析時，結構的剛度不隨拆橋階段造成的變形發生變化，但拆除階段由于扣索的反力，主拱圈截面剛度會隨著拆橋階段的不同而發生變化，所以不考慮主拱圈剛度的變化直接進行線彈性穩定性分析會讓計算結果偏于不安全。采用Newton-Raphson法對主拱圈的剛度進行實時更新，初始缺陷通過線彈性屈曲分析模態結構進行反向施加，作為考慮結構初始幾何缺陷的方法。定義缺陷比例因子為缺陷幅值與一階模態節點最大位移之比，通過判斷荷載位移曲線的突變點，作為計算幾何非線性的穩定系數依據。初始缺陷為L/1500時的荷載位移曲線見圖6，不同初始缺陷比例下的穩定系數見圖7。

根據計算結果可以看出，穩定系數隨著初始缺陷的不斷增加而不斷降低，可以看出初始缺陷在L/4000～L/1000時，其穩定系數降低了2%左右，降低并不多；但是當初始缺陷超過L/1000時，其穩定系數的降低程度明顯增大，可以按照2倍的安全系數設置二分之一L/1000的計算位移作為預警位移，通過實時監測橋梁的跨中位移作為安全監測手段之一，預防安全事故的發生。

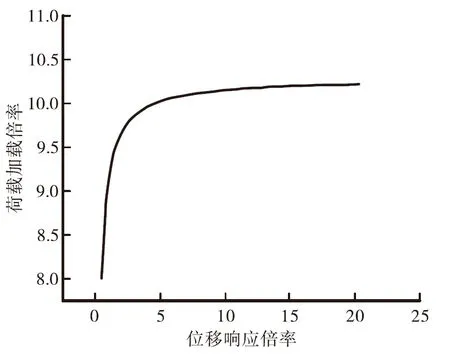
圖6 初始缺陷為L/1 500時荷載位移曲線

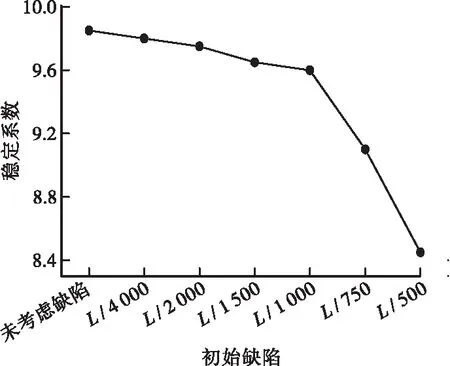
圖7 穩定系數隨初始缺陷變化趨勢

3 結論

以貴州某桁式組合拱橋作為研究對象，建立了拆橋階段的桁式組合拱橋有限元空間模型，以主拱圈拆除階段作為最不利階段施工階段進行分析，介紹了分析拱橋穩定的2種理論，并對其適用性進行說明，結合工程提出了桁式組合拱橋拆橋方案的主要原則，采用彈性屈曲理論對施工階段的主拱圈穩定性做出了分析，總結了前3種屈曲模態的形式以及對應的屈曲穩定系數。通過一階屈曲模態位移對主拱圈左邊進行修正來分析主拱圈結構的幾何非線性穩定性，綜合考慮施工過程中的不確定性，幾何非線性狀態對于拆橋結構的影響不可忽略，當缺陷比為L/1000時，安全穩定系數有明顯下降趨勢。