隧道爆破作用下上方管道的特征分析

陳志明, 鄧浩亮

(湖南路橋建設集團有限責任公司, 湖南 長沙 410004)

0 引言

我國交通運輸體系的發展日新月異、人民群眾的出行需求日益增長，為緩解地面交通堵塞和資源緊張的問題，涌現出越來越多的地下空間工程。目前國內山區的隧道修建主要采用鉆爆法，不僅經濟合理，且適用于各種復雜地質條件的地下空間工程中，但在方便隧道施工順利進行的同時，也不可避免對周圍環境造成破壞。所以在爆破施工前要特別注意爆破振動對周圍構筑物的影響，避免對周圍環境造成損害。尤其是爆破施工對管線周圍巖土體產生的擾動極易形成管線周圍土體的應力不均勻，導致地下管線自身的破壞[1-3]。

因此，在隧道修建過程中必須了解爆破振動對管線的影響，盡可能減輕不良影響，確保施工過程中管線的安全。目前，相關學者對于爆破振動下管線的動力響應特征主要采用數值分析結合現場監測的方法，并取得了一些成果。張坤等[4]利用數值分析軟件得到了不同爆心距下地下管線的應力峰值；石杰紅等[5]通過數值模擬軟件得出預裂孔可有效降低爆破對管線的振動；張志強[6]依托西氣東輸二線工程總結出采用導爆管延時起爆技術和V型網絡起爆技術，可防止爆破振動的疊加并有效減輕爆破振動所帶來的擾動。梁向前等[7]分析了工程爆破施附近供水氣管線的抗震特性，并結合現場爆破振動試驗和施工監測，研究了爆破地震波的傳播衰減規律和爆破振動對供水管線安全的影響。由此可見爆破振動對運輸管線擾動是事實存在的，因此需要提前進行預測振動效應并及時采取相應措施，降低爆破振動影響。

以某隧道工程正下穿管道為背景，通過數值分析提前對爆破振動效應進行預測，著重分析了管線豎直方向和水平方向上的爆破振速分布規律，并對管線在爆破振動作用下的應力進行分析。對隧道鉆爆施工的設計和實施進行指導。

1 工程概況

1.1 工程簡介

某隧道總長962m，設計為雙洞單向2車道，隧道進洞口位于丘陵坡麓，地形起伏大，表部覆蓋較薄的含角礫粉質粘土。隧道洞身為殘坡積、強風化 — 中風化巖體，裂隙較發育，巖質較硬，巖體破碎。地質參數如表1所示。隧道左右洞具有相似特征，隧道毛洞開挖寬度為16.8m，高度為8.6m，左右洞最大間距為16.59m，洞身大部分處于Ⅴ級圍巖段。在隧道樁號約K7+100處，山頂上有新修建的管道，管徑400mm，與本項目路線基本呈垂直交叉，距隧道拱頂垂直距離約34m，如圖1所示。其中管線埋深為2m，管壁材料為具有高強度和高韌性的X70鋼，參數見表2。據現場調查了解，該管道將不進行遷移，在該段位置施工時要需控制用藥量，盡量降低隧道爆破施工對管道的影響。隧道開挖掘進時嚴格按照新奧法原理進行施工。

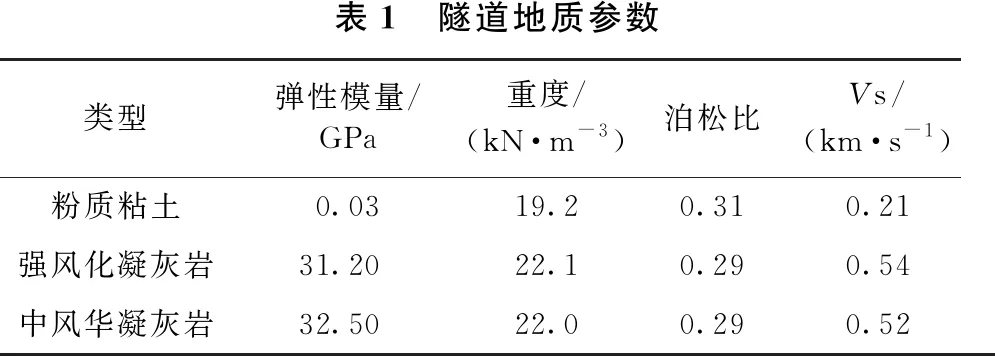
表1 隧道地質參數類型彈性模量/GPa重度/(kN·m-3)泊松比Vs/(km·s-1)粉質粘土0.0319.20.310.21強風化凝灰巖31.2022.10.290.54中風華凝灰巖32.5022.00.290.52

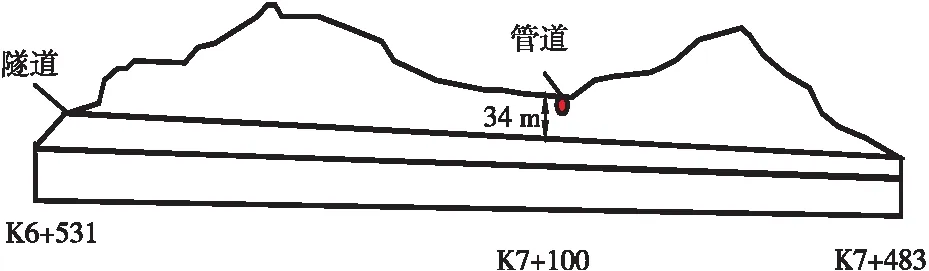
圖1 隧道縱斷面圖

表2 管道參數類型彈性模量/GPa屈服強度/MPa泊松比管道2121960.28

1.2 施工方案

本隧道穿越管線段處于Ⅴ級圍巖段，開挖時采用兩臺階預留核心土法，每循環進尺為1m。上部弧形導坑以機械開挖和弱爆破為主，開挖后及時施作初期支護，再對預留核心土采用控制爆破，最后開挖剩余土體及時進行仰拱施作。施工流程如圖2所示。施工時先對隧道進行超前加固，然后采用弱爆破法分部開挖，各部位開挖時周邊輪廓應盡量圓順，減少應力集中現象。

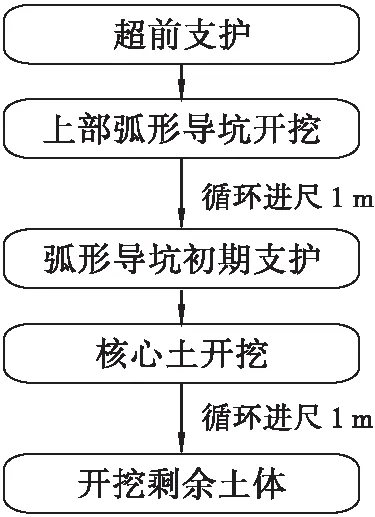
圖2 施工順序

隧道爆破的炮眼盡量采用不耦合裝藥結構或者間隔裝藥，以保證爆破質量和減震效果。不耦合裝藥是指炸藥直徑小于炮孔直徑，炸藥與炮孔壁之間留有間隙，以降低爆轟波作用在孔內壁上的初始壓力，使孔壁不壓縮破壞。本次爆破工程藥卷直徑為25mm，炮孔直徑為42mm，最大段裝藥量為8.2kg。裝藥結構如圖3所示。

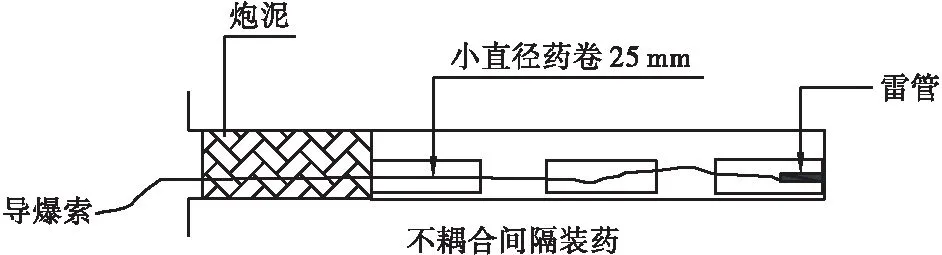
圖3 裝藥結構

2 爆破振動數值模擬

2.1 計算模型及參數

2.1.1模型的尺寸

采用非線性有限元程序LS-DYNA，針對爆破施工現場工程地質條件，在合理簡化的基礎上建立隧道-圍巖-管道的三維空間實體有限元模型。采用LS-DYNA自帶的高能炸藥材料*MAT_HIGH_EXPLOSIVE_BURN生成爆破地震波，計算分析得到隧道爆破開挖作用下爆破地震波在圍巖中的傳播規律和結構部位的速度、應力分布等動力響應特征。根據爆破動力響應研究的對象，模型分為管道和圍巖(含隧道)2部分。考慮到爆破振動對圍巖的擾動為3～4倍洞徑，模型縱向尺寸取86m，依據管線與隧道空間交叉的位置以K7+100為中心前后共取70m。管線的埋深為2m，隧道頂部距離管線的高度為34m。數值模型如圖4所示。

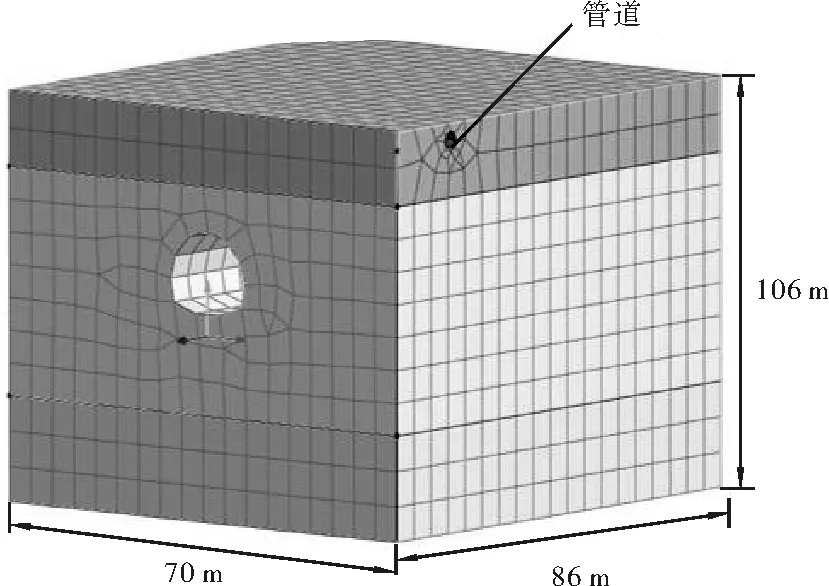
a) 三維模型圖

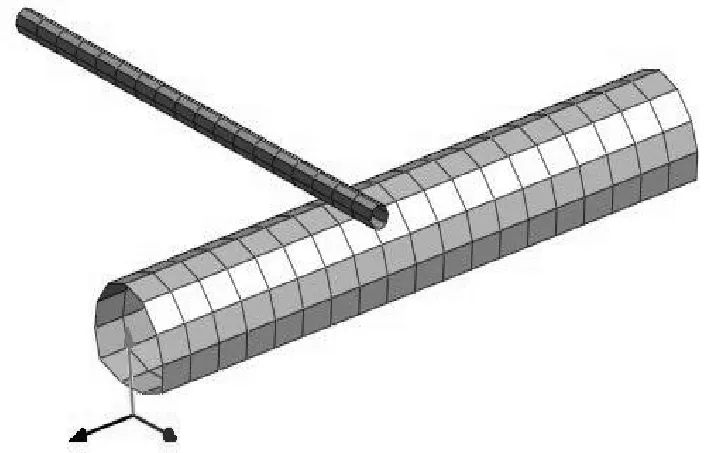
b) 管道與隧道位置關系

2.1.2模型參數

隧道圍巖采用的材料模型為MAT_PLASTIC_KINEMATIC，隧道圍巖材料參數如表3所示。

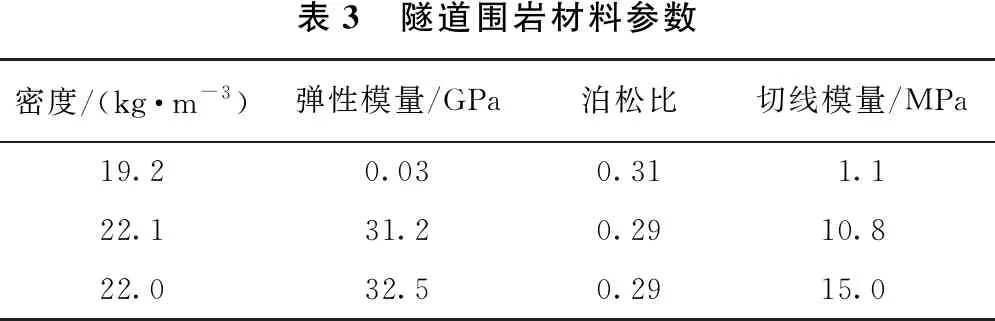
表3 隧道圍巖材料參數密度/(kg·m-3)彈性模量/GPa泊松比切線模量/MPa19.20.030.311.122.131.20.2910.822.032.50.2915.0

炸藥采用EOS_JWL狀態方程模擬炸藥爆轟過程中壓力與比容的關系，方程體現了炸藥做功能力：

(1)

其中，A、B、R1、R2、ω為方程材料參數；p為壓力，Pa；V為相對體積；E為單位體積初始內能。數值模型中所使用的炸藥材料與現場采用的巖石乳化炸藥一致，其主要輸入參數如表4所示。

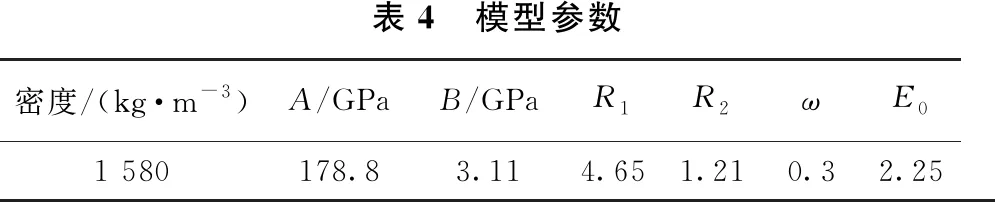
表4 模型參數 密度/(kg·m-3)A/GPaB/GPaR1R2ωE01 580178.83.114.651.210.32.25

管線為脆性材料,采用彈性和塑性2種斜率表示材料應力應變行為的雙線性各向同性硬化模型[6]，管線參數如表5所示。

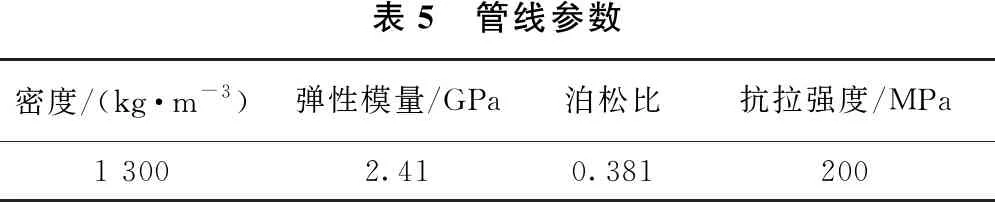
表5 管線參數密度/(kg·m-3)彈性模量/GPa泊松比抗拉強度/MPa1 3002.410.381200

2.2 邊界條件

所研究對象管道處于地下位置，假設管道周圍一定范圍內地基、坑洞等對研究對象無影響，管道處于無限且勻質的土壤內，由于模型大小有限，故在設定模型邊界時，除模型上表面為自由面的之外，其它所有面均為非反射邊界。為使管道、巖層和隧道等多種材料形成耦合，本模型采用ALE算法，炸藥劃分為Euler網格，管道和巖層劃分為Lagrange網格，Lagrange和Euler網格之間通過定義CONSTRAINED＿LAGRANGE＿IN＿SOLID關鍵字實現流固耦合[8],對管道、炸藥、隧道進行網格細化加密，隧道圍巖網格相對稀疏，保證其應力應變的精確模擬。炸藥和周邊圍巖采用8節點實體單元模擬，管道采用8節點板單元進行模擬，管道和圍巖單元之間具有相同的節點。

2.3 計算結果與分析

2.3.1管線振速分析

隧道樁號K7+100為隧道和管線交叉中心處，選取K7+100(Y=0時)為研究對象，模擬了該位置管線的動力響應特性。定義X為垂直于隧道軸線方向，即橫向；Y為隧道軸線方向，即縱向；Z為垂直于地表方向，即豎向，圖5為斷面測點分布。

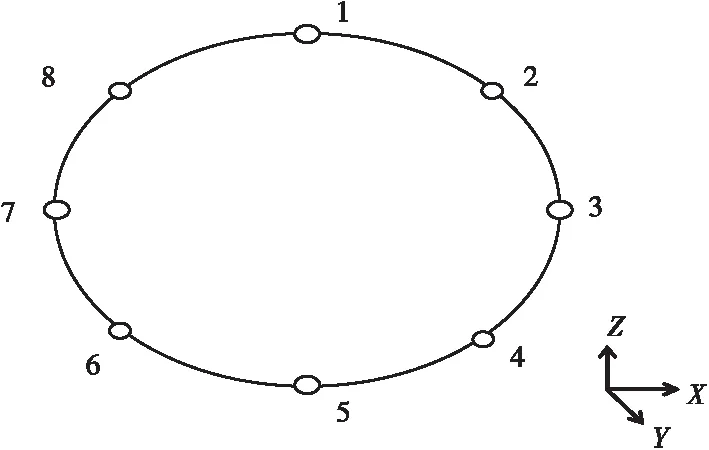
圖5 管線測點分布

表6為K7+100(Y=0)處測點的各個方向振速值。管道底部的峰值振速普遍比管道頂部側對應點的峰值振速值大很多，管道左右兩側對應點的峰值振速值差別較小；且同一測點X、Y方向振速值比Z方向峰值振速值普遍小很多，因此，豎向振速作為主要的判別依據。圖6為測點5各方向振速歷程圖。如圖6所示，測點振速幅值均隨著時間而逐漸衰減，衰減規律呈現先快后慢逐漸趨于平穩趨勢，且測點5各個方向最大振速均未超過《爆破安全規程》所允許的安全范圍3cm/s。

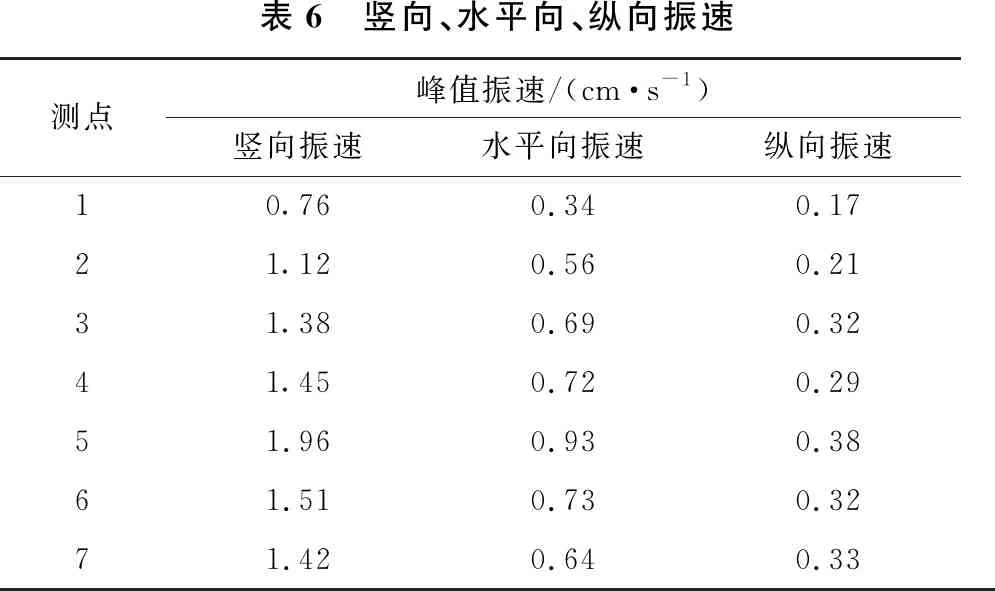
表6 豎向、水平向、縱向振速測點峰值振速/(cm·s-1)豎向振速水平向振速縱向振速10.760.340.1721.120.560.2131.380.690.3241.450.720.2951.960.930.3861.510.730.3271.420.640.33

a) 豎向

2.3.2管道應力分析

由上述可知，爆破振動能量隨著時間的增加逐漸衰減，選取t=15ms對管道進行應力分析。各方向應力云圖如圖7所示，可得X方向最大應力值為0.118MPa和Y方向最大應力值為0.089MPa，Z方向最大應力值為0.073MPa，X方向和Y方向的應力值都大于Z方向。

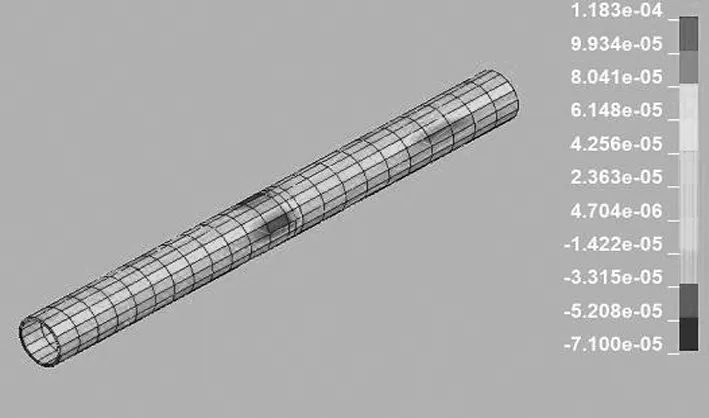
a) X方向

由此可知，在爆破過程中管線主要承受來自X和Y方向的應力，雖然Z方向上振動速度較大，但應力值較小。因此，振動速度并不能完全評價管道的動力響應和受力狀況。圖8為測點5各方向應力峰值與爆心距變化關系。爆心距小于20m時，應力值較大，衰減速度較快；爆心距大于20m時，應力值偏小，衰減緩慢。

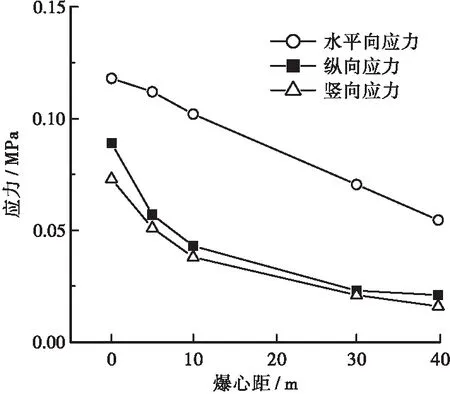
圖8 應力與爆心距關系

綜合上述結果分析，爆心距0m時，管線受爆破振動影響較大。雖然此時管線振動豎向速度未超過安全振動控制標準，但管線水平向和縱向上出現應力集中區域，需要引起重視。為最大程度降低爆破振動效應，爆心距小于20m時，要采取一定的爆破減振措施;大于20m時，可不改變爆破參數。

3 結論

1) 隧道爆破施工后，同一監測斷面爆破振動速度分布特征為：管底部>管左側>管右側>管頂部，且X、Y方向振速值比Z方向峰值振速值普遍小很多，故豎向振速作為主要判別依據。管線測點的振速幅值均隨時間而逐漸衰減，衰減規律呈現先快后慢，逐漸趨于平穩趨勢。

2) 爆破過程中管線主要承受來自X方向和Y方向應力，雖然Z方向上振動速度較大，但應力值較小。

3) 針對爆破振動對管線的影響，以20m水平爆心距為安全距離，小于20m時,要采取爆破減振措施。