基于熵權法的組合預測模型在路基沉降中的應用

李 文

(1.湖南理大交通科技發(fā)展有限公司， 湖南 長沙 410006; 2.湖南交通職業(yè)技術學院， 湖南 長沙 410006)

0 引言

目前，公路路基沉降的預測主要是根據積累的實測數據，通過合適的模型進行擬合分析，實現沉降預測，其預測效果主要取決于實測數據的準確性和模型選取的合理性。路基沉降變化在不同施工階段內有明顯差異，因此，在構建預測模型時可以考慮對多個單一預測模型進行組合，通過合理的權重分配來綜合各單項模型優(yōu)勢，取長補短[1-4]。本文根據項目路基沉降曲線的變化特點，研究不同施工階段內單一預測模型的擬合效果和誤差，對模型精度和適用性進行分析，以期找到一種科學、準確的預測方法。

1 工程概況

湖北省某在建高速公路，其路線地處長江中下游地區(qū)，所經區(qū)域以農田為主，局部溝塘較多，部分路段為軟土地基。經勘查分析，原地基存在軟弱夾層，不同路段地基土性質差異性較大，主要不良地質情況為軟土，該類土以淤泥、淤泥質土等為主，具有含水量高、壓縮性高、強度低等特點，由于地基在附加應力作用下發(fā)生排水固結，容易產生較大的沉降變形或差異沉降。

本項目軟基采取了分段、分措施處治，為了使沉降數據具有代表性，更好地反映本項目路基沉降的規(guī)律和特性，分別選取了3個典型填方斷面的沉降實測數據進行分析，典型斷面基本情況如表1所示。

表1 典型斷面基本信息典型斷面樁號填土高度/m處治方案1K12+4023.72砂墊層加超載預壓2K12+4764.58水泥粉噴樁3K12+5054.83粉噴樁加等載預壓

軟土路基在填筑過程中，隨著填土高度增加，荷載不斷增大，地基在附加應力作用下會發(fā)生排水固結，使整個路基出現持續(xù)沉降變形。其中，中樁位置沉降量要大于路肩處，因此可選取斷面中樁位置處的沉降數據對沉降過程和規(guī)律進行分析，典型斷面觀測點的實測累計沉降量與時間變化曲線如圖1所示。

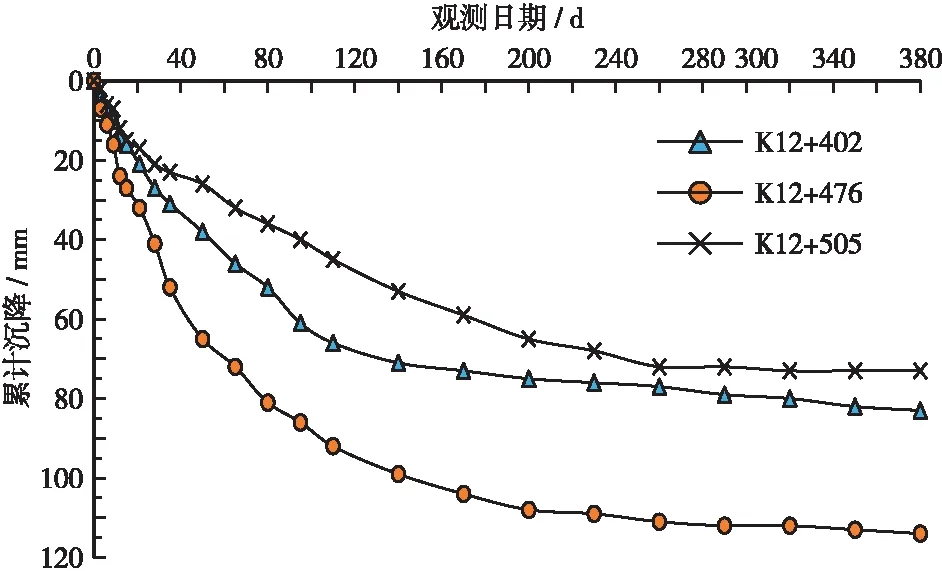
圖1 實測累計沉降-時間變化曲線

由圖1沉降變化曲線可知，不同處治措施的3個點位處的沉降變化趨勢基本相同。其累計沉降變化過程主要分為3個階段，分別為填筑期、恒載期和穩(wěn)定期。路基填筑期為0～120 d，該階段路基沉降速度較快，變化明顯；恒載期為路基填筑完成后的3個月左右(120～220 d)，沉降速率逐漸降低；穩(wěn)定期為220～380 d，此時沉降速率較小，沉降曲線也開始收斂，最終在380 d后達到基本穩(wěn)定狀態(tài)。

2 單一預測模型效果分析

結合本項目沉降曲線特點，參考同類型項目經驗，選擇項目所在地區(qū)工程實踐中較為常用的2種單一模型，即灰色GM(1，1)模型和Verhulst模型，分別就不同施工階段的沉降曲線進行擬合，對預測模型的特點和適用性進行分析。

2.1 單一預測模型

2.1.1GM(1，1)模型

GM(1，1)其預測值可以認為是預測曲線下最優(yōu)曲線的延伸，該模型具有無限增長的性質，模型表達式如下：

k=2，3，…，n

(1)

2.1.2灰色Verhulst模型

灰色Verhulst模型曲線呈“S”形，可反映路基沉降由前期加速變形到最終趨于穩(wěn)定的趨勢。Verhulst模型離散響應方程如下[6]：

(k=1，2，…，n)

(2)

式中:a、b為擬合參數，S(1)為原始沉降觀測數據，S(0)為S(1)經一次累減生成新數列，S(k)為第k次沉降數據。

2.2 實測數據等時距處理

由于現場實測沉降數據的時間間隔不一致，需要對原始數據進行等時距處理，本文采用拉格朗日插值方法，分別計算各個斷面等時距各天的沉降值[5]。

非等時距沉降增量時間序列為：

(3)

(4)

(5)

t=n時：

(6)

當t=2，3，…，n-1時，利用拉格朗日插值函數分段線形插值計算如下：

(7)

因此，等時距沉降數據時間序列：

(8)

按上述時距處理方法，選取沉降變化較大且特征較為明顯的3#斷面進行分析，以20 d為單位對原始數據等時距處理，等時距沉降數據如表2。

表2 3#斷面等時距處理后的沉降值序號時間/d累計沉降/mm序號時間/d累計沉降/mm12031.4611220108.7024056.0212240109.7136069.7413260110.8348080.3314280111.61510088.0315300111.96612094.1816320112.20714098.6717340112.708160102.2718360113.349180105.2719380114.0010200107.50

2.3 單一預測模型階段預測效果

分別選取不同施工階段內，累積實測數據序列中靠前的數據為樣本計算模型參數，并預留1組數據與模型預測值進行比對對單個預測模型的適用性和效果進行分析。

對填筑期6組沉降數據進行回歸分析(見表3),模型擬合相對誤差對比見圖2。

表3 填筑期單一預測模型分析結果序號天數/d實測值/mmGM(1,1)模型Verhulst模型擬合值/mm相對誤差/%擬合值/mm相對誤差/%12031.4631.46—31.460 0—24056.0258.594.5951.966 7-7.2436069.7467.54-3.1569.972 50.3348080.3377.85-3.0981.060 10.91510088.0389.731.9386.469 1-1.77612094.18103.43(預測值)9.8289.767 2(預測值)-4.69

圖2 填筑期預測模型擬合相對誤差

由表3可以看出，路基填筑階段采用GM(1,1)模型和Verhulst模型進行擬合，二者擬合值的相對誤差均保持在10%以內，整體預測效果較好。GM(1，1)模型擬合值變化速率較大，主要表現為正向偏大，而Verhulst模型擬合值整體偏小且變化較平穩(wěn)。根據圖2，對模型的相對誤差進行對比發(fā)現，2種模型的相對誤差正負走向相反，存在誤差的互補可能性。

路基持續(xù)填筑至設計高度后停止填土，直至鋪筑路面前，此時荷載處于相對穩(wěn)定，進入恒載狀態(tài)，對該階段內的12組沉降數據進行回歸分析(見表4)，模型擬合相對誤差對比見圖3。

由表4和圖3可以看出，進入恒載期后，隨著實測數據的增多，GM(1，1)和Verhulst模型的平均相對誤差分別為6.70%和4.51%，擬合效果有一定的提升。對單點預測值(12號)進行分析可知，GM(1,1)模型的預測值為123.43 mm，相對誤差為12.51%，Verhulst模型預測值為106.51 mm，相對誤差為-2.92%，從誤差絕對值上看，GM(1,1)模型預測值明顯偏大，Verhulst模型更接近實測值，但預測值較小，結果偏保守。

表4 恒載期單一預測模型分析結果序號天數/d實測值/mmGM(1,1)模型Verhulst模型擬合值/mm相對誤差/%擬合值/mm相對誤差/%12031.4631.46—31.46—24056.0269.5224.1046.60-16.8236069.7473.635.5862.92-9.7848080.3377.98-2.9377.58-3.42510088.0382.59-6.1888.720.78612094.1887.47-7.1296.182.12714098.6792.63-6.12100.742.108160102.2798.11-4.07103.381.099180105.27103.90-1.30104.87-0.3810200107.50110.042.36105.69-1.6811220108.70116.547.21106.13-2.3612240109.71123.43(預測值)12.51106.51(預測值)-2.92

圖3 恒載期預測模型擬合相對誤差

在施工完成后路基進入穩(wěn)定期并逐漸達到基本穩(wěn)定狀態(tài)，此時沉降速率逐漸趨近為0，累積沉降曲線尾端開始收斂，對路基填筑至穩(wěn)定期內的全過程的18組沉降數據進行回歸分析(見表5)，模型擬合相對誤差對比見圖4。

由表5和圖4分析可知，以該斷面路基沉降全過程數據為樣本進行預測時，2種模型的早期擬合數據變化速率較快，具有較明顯上升趨勢，中后期變化速率相對降低，但GM(1,1)模型仍保持持續(xù)增長，Verhulst模型則逐漸收斂。從后3組預測值可以看出，GM(1,1)模型預測值增長速度仍然較大，而Verhulst模型增速則趨近0，與現場實際情況相符，整體上Verhulst模型擬合效果較好，更適用于中長期預測。

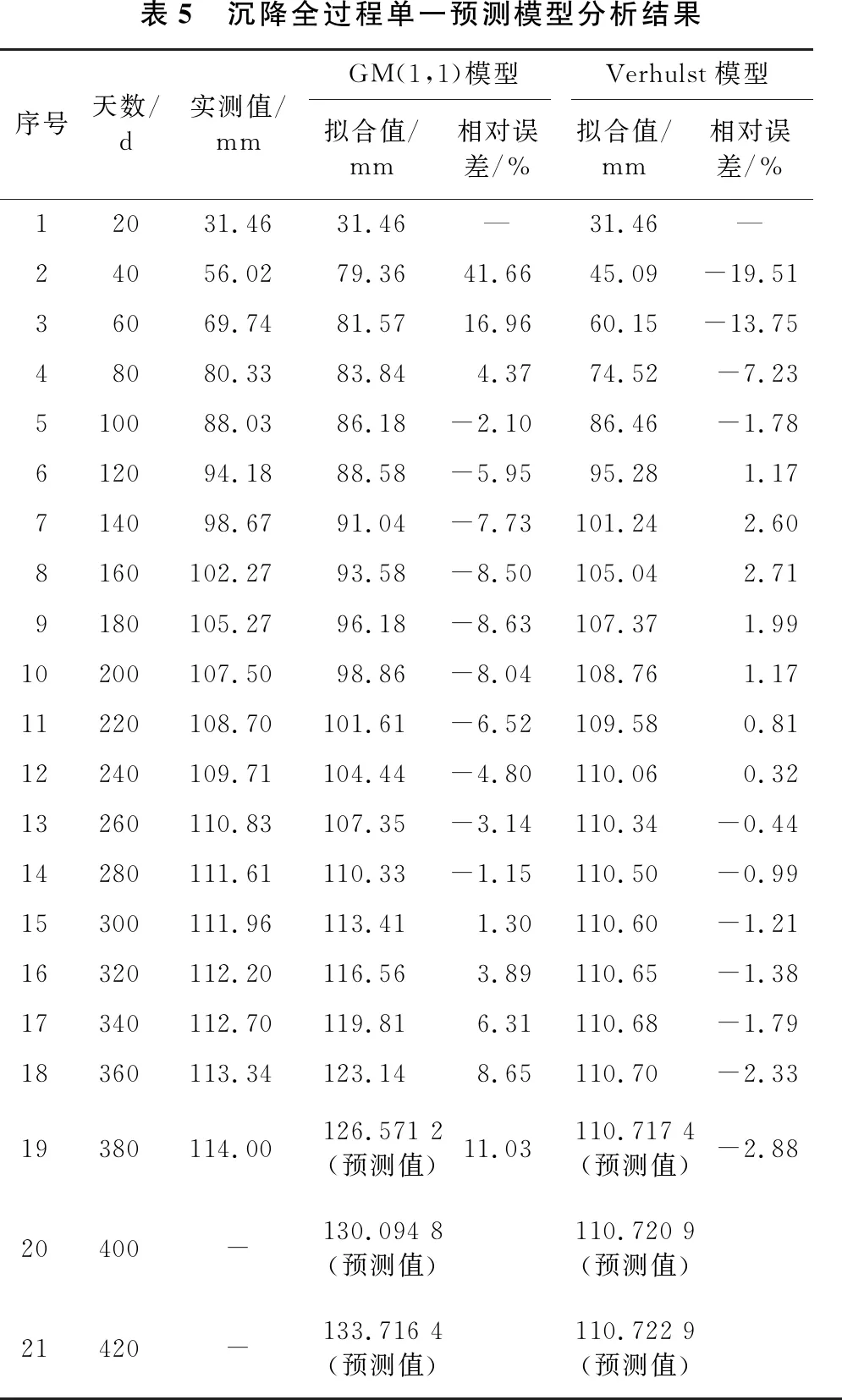
表5 沉降全過程單一預測模型分析結果序號天數/d實測值/mmGM(1,1)模型Verhulst模型擬合值/mm相對誤差/%擬合值/mm相對誤差/%12031.4631.46—31.46—24056.0279.3641.6645.09-19.5136069.7481.5716.9660.15-13.7548080.3383.844.3774.52-7.23510088.0386.18-2.1086.46-1.78612094.1888.58-5.9595.281.17714098.6791.04-7.73101.242.608160102.2793.58-8.50105.042.719180105.2796.18-8.63107.371.9910200107.5098.86-8.04108.761.1711220108.70101.61-6.52109.580.8112240109.71104.44-4.80110.060.3213260110.83107.35-3.14110.34-0.4414280111.61110.33-1.15110.50-0.9915300111.96113.411.30110.60-1.2116320112.20116.563.89110.65-1.3817340112.70119.816.31110.68-1.7918360113.34123.148.65110.70-2.3319380114.00126.571 2(預測值)11.03110.717 4(預測值)-2.8820400-130.094 8(預測值)110.720 9(預測值)21420-133.716 4(預測值)110.722 9(預測值)

圖4 沉降全過程預測模型擬合相對誤差

綜上所述，在不同路基施工階段中沉降表現出一定的階段性，GM(1，1)模型能夠較好的反映路基填筑期沉降變化，Verhulst模型則更適合中長期預測。在不同的沉降階段，2種預測模型相對誤差變化趨勢不同，GM(1，1)模型誤差較大，且主要為正向增加，Verhulst模型整體誤差較小，擬合值也相對偏小，二者適用范圍且具有一定的互補性。

3 熵權法組合預測模型

3.1 組合模型構建

通過對2種模型擬合值效果和誤差進行分析，考慮預測擬合值與實測值之間的殘差及相對誤差之間具有不確定性特點，采用熵權法來構建組合模型，提高預測精度和模型的適用范圍。熵權法的基本原理是用熵來表征系統(tǒng)無序程度，如果指標的信息熵越小，該指標提供的信息量越大且權重越大。熵權法中對于某預測問題，選用的第i種單項預測模型在第t時刻得到的預測值與實測值之間的相對誤差可表達為：

(9)

式中：i=(1，2，3,…,m)；t=(1，2，3,…,n)；xit為第i種單項預測方法在第t時刻得到的預測值。

權值具體計算方法如下：

1) 計算第i種單項預測方法的預測值與實測值在t時刻的相對誤差比重

(10)

(11)

2) 根據熵值與其變異程度相反的原則，求相對誤差變異系數

di=1-hi

(12)

3) 再得單項預測模型的加權值

(13)

由式(13)計算出權系數后，組合預測模型表達式為：

(14)

單項預測誤差序列的熵值越大，其變異程度越小、權值越大。熵權法充分考慮了不同預測方法相對誤差的大小，對組合預測模型的權重進行分配，使單一模型之間能夠相互補充，權值確定結果，見表6。

3.2 預測模型效果對比分析

本文選用的預測模型均屬于曲線回歸法，即基于實測數據采用回歸計算的方法反算模型參數，可采用相關系數和相對誤差對模型精度進行評價，根據熵權法確定GM(1，1)模型和Verhulst模型的權重值，計算相關系數R和預測值的相對誤差結果見表7。

表6 權值計算結果預測模型權值分配填筑期填筑-恒載期全過程GM(1,1)模型0.3590.3960.403Verhulst模型0.6410.6040.597

表7 組合模型和單一模型效果評定預測模型填筑期填筑-恒載期全周期相關系數R相對誤差/%相關系數R相對誤差/%相關系數R相對誤差/%GM(1,1)模型0.970 5 9.820.901 2 10.300.837 8 11.03Verhulst模型0.987 9 -4.690.991 2 -2.920.990 8 -2.88組合模型0.999 7 1.060.994 2 2.320.993 9 2.02

由表7可知，組合模型在路基沉降各個時期中較單一模型而言具有良好的擬合效果，且預測值相對誤差保持在2%左右，相關系數R值保持在0.99以上，具有較高的預測精度。組合模型曲線變化由權系數分配較大的單一預測模型控制，另一種模型作為完善和補充，使組合模型曲線與實測結果更為接近，體現了組合預測模型的優(yōu)越性。此外，組合模型可根據實測數據的變化特點，對權重分配和調整，具備良好的適用性。

4 結論

本文根據路基沉降實測數據變化特點，按施工階段的不同，對灰色GM(1,1)和Verhulst 2種模型的擬合效果和適用性進行了分析，并對預測值與實測值之間相對誤差進行了研究，構建了組合模型，主要結論如下：

1) 該項目路基累計沉降變化具有明顯的階段變化，GM(1，1)模型能夠較好的反映路基填筑期的沉降變化，而Verhulst模型則更適用于中長期預測。從模型整體的相對誤差進行對比發(fā)現GM(1，1)模型相對誤差較大，Verhulst模型誤差較小，2種中預測模型相對誤差變化不同，具有一定的互補性。

2) 基于熵權法構建的組合預測模型具有可行性和有效性，權值確定過程中考慮單一預測模型中預測值與實測值的相對誤差不確定性，綜合了單一模型的優(yōu)勢，預測效果有明顯提升。驗證結果表明，組合模型在路基沉降的各階段中均有較好地擬合效果，預測值相對誤差保持在2%左右。同時，組合模型可根據項目沉降曲線的變化特點，對權重進行靈活調整，具備更好的適用性，可為同類型路基沉降預測提供參考。