“大單元整體教學”視野下的教學結構分析
——以《認識比》為例

■廣東省江門市蓬江區教師發展中心 黃肖慧

小學數學大單元整體教學，就是審視數學教材的自然單元，將有內在知識聯系的單元內容構成整體，并且根據學生的認知規律，組織系統化、科學化的課堂教學。教學結構分析作為單元整體教學中的重要因素之一，直接影響教學過程的實施與學生認知結構的形成。那么，如何開展單元整體教學結構分析呢？經過梳理和提煉，我以為，主要從單元各例題之間的教學路徑、單元內容在不同學段的起源與發展、認知基礎與知識結構融通三個維度展開研究。下面以人教版六年級上冊《認識比》為例展開闡述。

一、明晰單元各例題之間的教學路徑

在《認識比》單元中，“比”無疑是單元核心概念。從實驗版教材“兩個數相除又叫作兩個數的比”到修訂版教材“兩個數的比表示兩個數相除”，可見“兩個數相除”與“兩個數的比”既有聯系，又有區別。有自身的特點、意義和價值，修訂版教材更加強調兩個量之間的“倍比關系”。

解讀例題，了解單元內容各例題之間的教學路徑，是一種解構行為。解讀過程中，要思考以下問題：單元的核心內容、核心概念是什么？本單元一共有多少個例題？各例題之間有怎樣的教學關系？例題的問題情境想表達什么？建構以核心概念為中心的邏輯結構，分析教材中例題之間的聯系及教學目標，有利于教師整體規劃課時，制定具有聯系、結構化的教學目標。

二、理清單元內容在不同學段的起源與發展

審視與研讀知識在單元、年級、學段的分布，意在了解整個小學階段“比”相關內容的呈現序列，梳理知識之間的起源與發展。下面以人教版數學教材“比”及其相關知識學習為例，說明其在不同學段的起源與發展（見表1）。

（一）起：“比”起源于除法與“倍”

兩個數的比表示兩個數相除。追溯到二年級下冊“除法的初步認識”，除法意義中的“包含除”，表示的就是兩個數的比，如把8條紅金魚每2條放在一個魚缸里，需要幾個魚缸？這正是兩個同類量的比的原型。“比”既表示同類量的比，又表示不同類量的比。其中，同類量的比和“倍”有著密切的關系。例如雞有10只，鴨子有15只，可以用15÷10表示鴨子數量是雞的多少倍，也可以用“15比10”表示鴨子數量與雞的只數比；可以用10÷15表示雞的只數是鴨子的幾分之幾，也可以表示雞的只數與鴨子只數的比是“10比15”。可見，“比”起源于除法與“倍”。

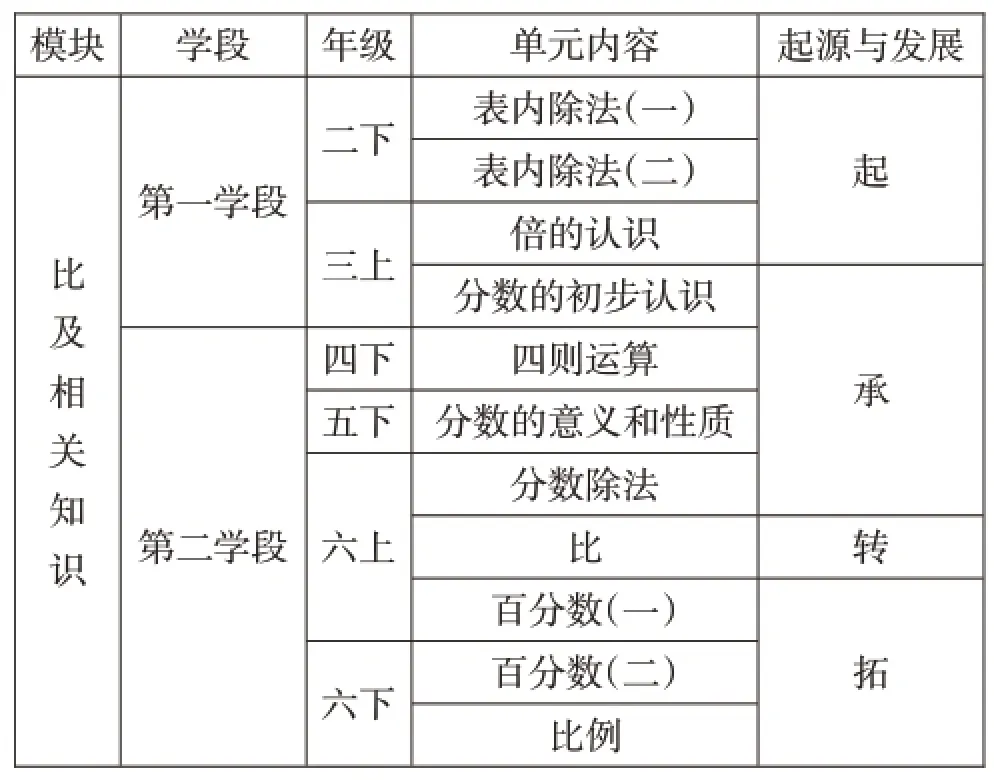
表1“比”及相關知識的起源發展

（二）承：分數相關知識是“比”的重要承托

從《分數的初步認識》到《分數的意義》再到《分數除法》，通過兩年的學習，學生逐步理解了分數意義和性質，也能聯系分數的含義解答求一個數是另一個數的幾分之幾等實際問題，這些都是學生理解比的知識的重要承托。通過分數相關知識的學習，有助于學生溝通分數、除法與比的聯系，豐富和加深對分數和除法的理解，進一步提高分析和解決實際問題的能力。

（三）轉：遷移轉化是學習“比”的關鍵

“比”借助除法之勢，由“倍”導入，通過遷移轉化為兩個同類量的比，進一步推廣至不同類量之比。但是“兩個數相除”與“兩個量的比”并不等價，表現為：一是除法中包含除有“比”的內涵（兩個同類量的比），而均分除只指向一個量，不含有“比”的內涵；二是“比”是兩個變量之間的不變關系，重點表現一種狀態，而除法是一種運算，趨向運算的形式和結果，“比”只有求比值時才利用除法進行運算；三是“比”與除法均源于度量，如長度、面積、時間等都可度量，量與度量單位的度量結果表現為“比值”或“商”，同時，“比”還可以表示濃度、顏色、質地等不可度量的比，即兩個不同類量的比。

（四）拓：《百分數》與《比例》是《比》的拓展與深化

“比”可以擴展為變量之間的正比例函數關系，而《百分數》的學習，又使除法、分數、比、百分數、比例形成了緊密的關系網，讓我們看清了“比”的前世今生。

三、實現認知基礎與知識結構的融通

小學數學單元整體教學結構分析，既要重視數學知識結構（客體）的分析，更要重視學生認知基礎（主體）的分析，并通過對數學知識結構與學生認知基礎的融通分析，使教學主體、客體達成對立統一的平衡。要了解學生的認知基礎，不能僅僅依靠過往教學經驗，需要一定的調研。

以《認識比》為例，我們采用了訪談的方式對40位六年級學生進行前測。測試結果顯示，約68%的學生能列舉“比”的例子，24%的學生列舉了體育賽事的比分，還有約8%的學生把“比”與“比例”混為一談。只有15%的學生能用“倍比”解決問題，約有20%的學生用差比關系解決問題，37%的學生無法解決問題。只有5%的學生能聯系“倍比”“相除”關系解釋“比”。

以上測試數據反映，學生對“比”的認識絕大多數停留在生活層面，對“比”的意義缺乏本質的認知。教學中，教師應摒棄過去對“比”概念的字面形式解讀，著力解決兩個問題：1.引導學生理解“兩個數相除”與“兩個數的比”之間的區別與聯系；2.體會為什么要學習“比”，體會“比”的本質與價值。在這一過程中，從“除法—份數—分數”大單元關系結構中，突出“每一份相等”“份數對等”的關系尤為重要。