基于有限元強度折減法公路深路塹邊坡穩定性分析

任雁飛， 劉夢雅

（1.天津市市政工程設計研究院 四川分院，四川 成都 610041；2.中國電建集團成都勘測設計研究院有限公司，四川 成都 610072）

隨著我國高速公路路網建設的進一步推動，不可避免地遇到越來越多深路塹邊坡。由于深路塹邊坡復雜的地質條件、較大的高度及坡度，經常在施工及后期運營時期發生失穩災害，造成安全隱患，因此對邊坡進行穩定性評價分析尤為重要。

國內外對邊坡工程的穩定性分析已有諸多方法及理論。20世紀20年代初期，相關學者主要利用傳統的工程經驗對邊坡穩定性進行定性分析；隨著研究深入，逐漸發展到使用極限平衡法對邊坡穩定性進行定量分析的階段[1～2]；近些年，結合非確定性分析方法從不同的視角和學科領域提出不同的理論應用于邊坡穩定性分析研究中，如概率法、模糊理論、灰色關聯理論、人工神經網絡、遺傳算法等[3～5]。但這些方法都存在某些方面的不足之處，如：工程經驗法欠缺準確性且無法提供量化指導；極限平衡法沒有考慮坡體中應力-應變的關系，需要先假定滑動面的位置，最終邊坡計算結果可能會與實際情況產生很大誤差；非確定性分析方法對于評價指標的選擇存在爭議，數據樣本的不足也會造成結果不準確等問題。

隨著計算機技術的發展以及對巖土體本構模型研究的深入，很多數值模擬方法被廣泛應用在工程地質和巖土工程領域，在探索邊坡應力-應變問題及穩定性分析領域取得了突破性的進展，眾多的數值分析方法中以有限元法最為突出[6～7]，其適用范圍廣，結果精確。

1 有限元強度折減

1.1 有限元強度折減原理

有限元強度折減法對邊坡的穩定性進行分析，是一邊降低邊坡巖土體的抗剪切強度參數，一邊觀察其破壞狀態，直至達到極限破壞狀態。此時有限元的程序會根據彈塑性的計算結果得到破壞的滑動面，同時可以得到邊坡的強度儲備安全系數[8]。有限元強度折減的基本原理是，用表征巖土體的強度指標c、φ值同時除以折減系數F，得到的新的c′、φ′值，c′即折減后的黏聚力、φ′即折減后的內摩擦角；將其作為新的材料強度參數用于有限元極限試算中，通過不斷加大折減系數F降低c、φ值，當達到破壞狀態時，其對應的最終折減系數F即為有限元強度折減法下的邊坡穩定性安全系數[9]。

1.2 本構模型

在有限元分析中可以考慮各種復雜的本構模型。一般路面邊坡穩定性的研究，主要考慮力和強度的分析，對位移的要求相對較低，故而對本構關系的選擇不必十分嚴格，在目前的工程分析當中，普遍采用的模型為理想彈塑性本構模型。

按增量理論，土體的彈塑性應力-應變關系為

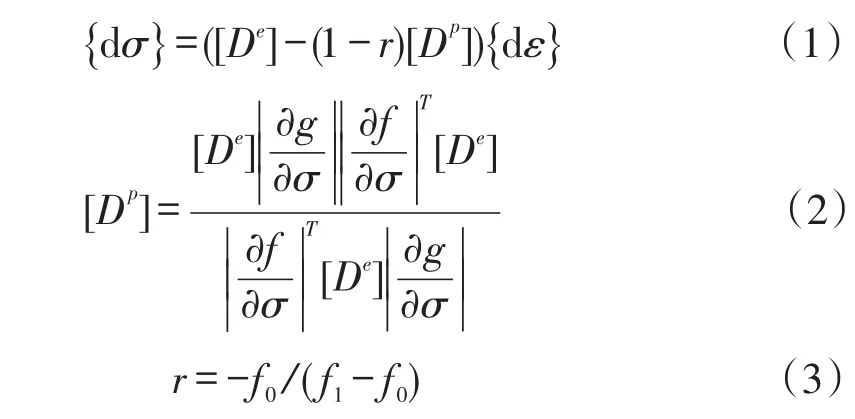
式中：[De]為彈性矩陣；[Dp]為塑性矩陣；f0為彈性變形初始應力狀態對應的屈服函數值；f1為塑性變形應力狀態對應的屈服函數值。當r=1時，對應彈性矩陣；當r=0時，對應完全塑性矩陣，當0＜r＜1時，表示單元由彈性向彈塑性狀態轉變，對應彈塑性矩陣。

1.3 屈服準則選用

雖然對本構關系的選擇不嚴格，但數值模擬中的屈服準則選用對所求安全系數的結果有密切影響，目前常用的是摩爾-庫倫準則與Drucker-Prager準則。

摩爾-庫倫準則的屈服面在主應力空間為不規則六角錐面，這種屈服形式更適用于描述巖土體的屈服和破壞特征，Drucker-Prager準則在三維應力空間中是連續的函數，在此條件下應用有較高的精度，適用于三維空間且著重考慮靜水壓力對巖土特性影響的問題，考慮到本文著重模擬施工開挖過程邊坡穩定性狀況，因此選用摩爾-庫倫屈服準則更為合理。

1.4 有限元中路塹邊坡失穩的判斷標準

目前對于邊坡失穩破壞的判斷標準主要有：有限元計算不收斂，塑性區貫通，塑性應變或位移突變。對這3種判據的選用學術界目前還存在著爭議，沒有明確統一的定論[10]。

從破壞現象上看，邊坡失穩，滑體滑出，滑體由穩定靜止狀態變為運動狀態，滑面節點位移和塑性應變將產生突變，此后位移和塑性應變將以高速無限發展，這一現象符合邊坡破壞的概念，具有明確的物理意義。

綜上所述，本文以監測特征點位移突變處對應的安全系數作為有限元模擬邊坡穩定性計算結果。

2 邊坡開挖有限元模型的建立

2.1 建模計算過程

京新高速張家口段K23+580左側深挖路塹由于左側開挖邊坡較高，最大切坡高度40 m，邊坡采用臺階形式，分4級開挖。第一、二級開挖邊坡坡率為1∶1，高度均為12 m，第三、四級開挖邊坡坡率為1∶1.5，高度分別為10、6 m，每級邊坡在變坡點設置寬度為2 m的平臺。見圖1。

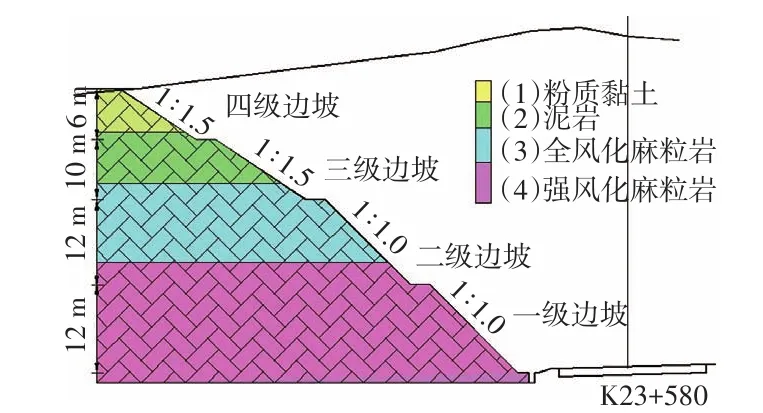
圖1 邊坡典型斷面

采用ABAQUS有限元分析軟件進行數值模擬。第一步模擬第四級邊坡的開挖，第二步模擬第三級邊坡開挖，第三步模擬第二級邊坡開挖，第四步模擬第一級邊坡開挖。穩定性動態模擬過程基本思路：

1）對未開挖初始狀態下的邊坡施加重力，運用Geostatic分析步進行地應力平衡，運算得到邊坡巖土體自重作用下的應力場，作為邊坡的初始應力場；

2）移除第一步開挖的邊坡巖土，重新施加重力荷載，得到該開挖步的應力應變場；

3）通過調整模型材料參數的場變量來實現強度折減法的應用，以坡腳監測點位移速率突變作為邊坡失穩的判斷標準，得到該階段邊坡有限元模擬的穩定安全系數；

4）依據上述步驟，進行第二步、第三步、第四步開挖后的邊坡模擬。

2.2 參數選定

路塹邊坡巖土體初始狀態下物理力學參數見表1。

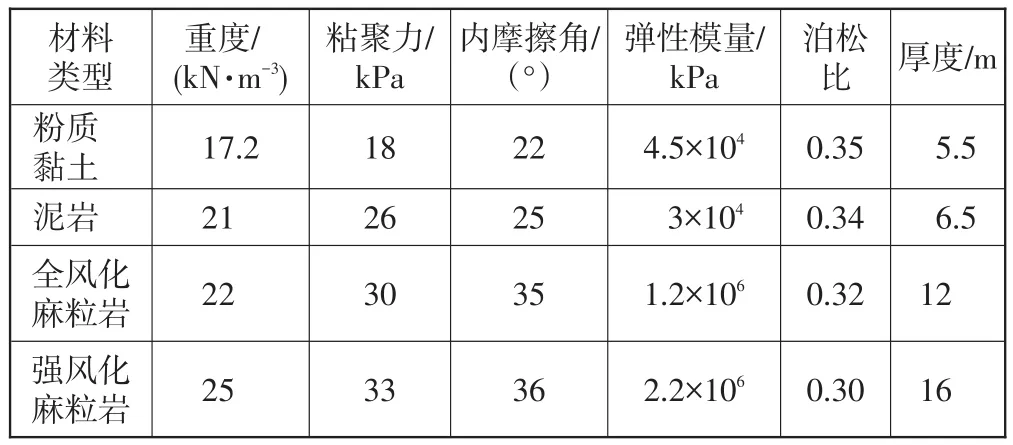
表1 邊坡模型計算參數

2.3 模型邊界條件定義

設定模型巖土體水平方向不產生側向移動，但是可沿豎直方向產生移動；底部邊界不產生任何移動，設置為雙向標準固定約束；頂面自由。為提高計算精度，設置左右邊界從坡腳和坡頂線各向外延伸35 m，下邊界從路面標高向下延伸40 m，即總高度取為2倍坡高。為計算方便，將模型幾何尺寸取整：X=0，X=110；Y=0，Y=80。

2.4 模型網格劃分

本文將邊坡變形問題視為二維平面應變問題，通過建立4個數值模型來實現邊坡四級開挖過程的分析，殼單元，四邊形，選擇劃分技術為Sweep，在Ele?ment Type中，選用CPE4（四節點平面應變單元）作為單元類型，使計算結果符合二維模型變化規律，同時考慮到不同地層巖性影響，將巖層界面作為網格單元控制線，網格劃分后最終得到初始單元數為2 740個。

3 模擬結果分析

3.1 穩定性

基于強度折減系數法、屈服破壞準則，對開挖過程中的4個階段進行模擬分析，見圖2和圖3。

圖2 各級邊坡坡腳水平位移與折減系數關系

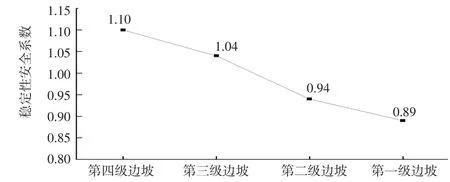
圖3 開挖過程邊坡穩定安全系數

由圖2可以看到，各級開挖階段位移突變點位置及對應場變量數值。而由圖3可以看出，隨著施工進程邊坡穩定系數不斷降低。

3.2 位移

采用彈塑性強度折減有限元法對路塹邊坡在各級開挖階段進行模擬，模型計算處理后輸出的邊坡四級開挖水平位移情況，見圖4。

圖4 位移

由圖4可以得出：

1）隨著開挖的推進，邊坡整體水平位移越來越大，由第四級邊坡開挖后坡腳最大水平位移3.775 mm到第三級邊坡開挖后的坡腳最大水平位9.065 mm，在第二級邊坡開挖后坡腳最大水平位移陡然增加到了1.732 cm，此時邊坡穩定性安全系數也是下降幅度最大的階段，到第一級邊坡開挖后坡腳最大水平位移最終為3.781 cm，此時的邊坡穩定系數為所有開挖階段最低；

2）整個邊坡的位移區域近似為圓弧狀，從單個邊坡位移云圖上可以看出，坡腳附近位移最大，這是因為剪應力在坡腳處集中，所以邊坡滑移面也多從坡腳處發起，因此坡腳附近水平位移最大；

3）雖然邊坡的上部土層（第四系中粉質黏土層和中風化泥巖層）材料強度低，但當開挖深度較大后，邊坡的位移主要集中在邊坡的中下部，除了坡腳應力集中原因外，上部邊坡坡度設計較下部坡度緩也是其原因之一。

3.3 塑性應變

在數值模擬過程中，ABAQUS可以輸出單元高斯點上的塑性應變量（PEMAG）。

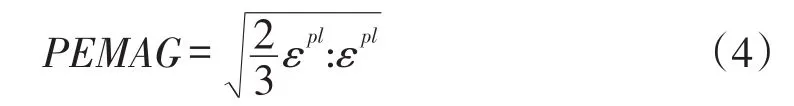
式中：εpl為高斯單元點上的塑性應變張量。

邊坡四級開挖后的塑性區應變及所有邊坡開挖完成后，根據不同折減系數的邊坡塑性區變化見圖5和圖6。

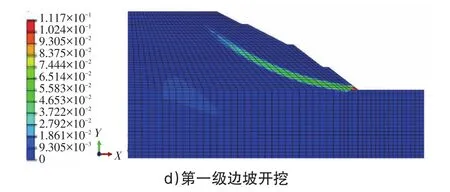
圖5 各階段開挖邊坡塑性區變化

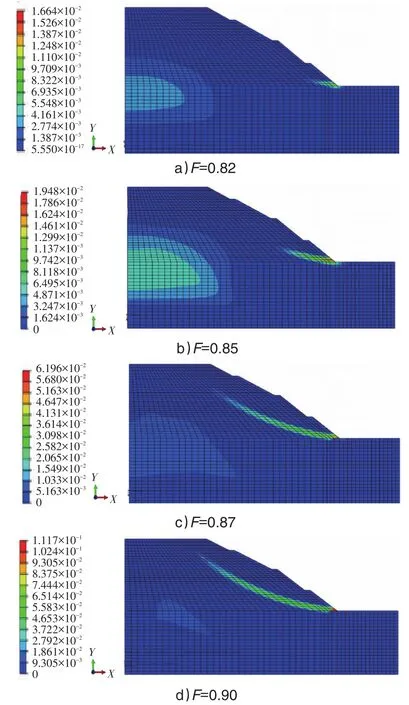
圖6 不同折減強度下邊坡塑性變化

由圖5可以看出，邊坡塑性應變較大區域出現在坡腳附近，這是由于坡體自重導致坡腳應變集中。第一層開挖處，土層主要為粉質黏土層，其c、φ值較小，導致邊坡塑性區未深入內部，在自由表面產生了塑性變形，隨著開挖深入，塑性區深入到邊坡內部，同時邊坡上層臨近自由面處應變大大減少甚至出現無應變現象，當邊坡發生失穩現象時，坡腳會較早的出現裂縫，在對邊坡進行穩定性監測時，應著重關注邊坡坡腳附近的區域。

塑性應變值的大小反映了潛在滑動面發展為實際滑動面概率的大小，塑性應變值越大，潛在滑動面發展為實際滑動面的可能性越大，這四級開挖邊坡塑性應變值分別為 1.192×10-2、4.158×10-2、4.643×10-2、1.117×10-1，因此這四級開挖邊坡發生滑動的可能性也是依次增加的，這與穩定性系數依次下降的規律相吻合。第二級邊坡開挖，帶狀塑性區在第二級邊坡中部出現不連貫的現象，經分析是因為此處為不同性質土體的分界處，從而產生了薄弱面，造成軟件模擬時此處應變狀態重分布。因此在開挖過程中，不同土體分界處可能容易產生變形薄弱區域。

由圖6可以看出，隨著折減系數F的增加，邊坡模型的塑性區域增大，清楚地反應了邊坡塑性區的發展趨勢，這也是強度折減法比極限平衡法優越的原因，同時塑性區域代表著剪切破壞帶的位置，其形狀近似為圓弧狀，與極限平衡法提出的結論相符，因此邊坡的塑性區域可以用來表征邊坡失穩的滑動帶位置。

4 結論

1）隨著施工的推進，路塹邊坡穩定性安全系數不斷下降，同時邊坡整體的水平位移逐漸增加，坡腳附近是位移變形最大的地方，開挖過程中坡腳位移增幅與邊坡穩定性安全系數的下降趨勢相同。

2）邊坡的破壞由坡腳開始逐漸向坡頂發展，坡腳附近為塑性應變較大區域，邊坡發生失穩時，坡腳會較早的出現裂縫，同時在不同性質土體的分界處出現應變突變情況，容易產生薄弱面，因此邊坡穩定性監測的重點應當放在坡腳及地層巖性發生變化的界面處；通過調整折減系數值得到的圓弧狀塑性區域可以用來表征邊坡失穩滑動面位置。